小學“圓的面積”教學蘊涵的數學學科核心素養

魏閑妹 廖運章

[摘要]以人教版教材六年級上冊“圓的面積”為例，結合《普通高中數學課程標準（2017版）》提出的數學學科核心素養的內涵，從生活情境、合情推理、知識可視化三個方面，揭示現實情境視角下“圓的面積”教學中所蘊涵的數學學科核心素養。

[關鍵詞小學數學;圓的面積;數學核心素養;割補轉化

[中圖分類號]G623.5

[文獻標識碼]A

[文章編號]1007-9068（2020）32-0029-03

“圓的面積”是義務教育階段“圖形與幾何”部分的重要內容，要求學生通過觀察、操作、探索等活動，掌握圓的面積公式，并能解決簡單的實際問題。“圓的面積”這一課是學生在現實情境下經歷從操作驗證走向推理論證，實現數學“再創造”的過程，是學生積累數學活動經驗和發展數學核心素養的有效課程。

本文將以人教版小學數學教材六年級上冊5.3節“圓的面積”為例，結合《普通高中數學課程標準（2017版）》提出的數學學科核心素養的內涵，通過剖析生活情境、可視化圓的面積公式推導等過程，揭示現實情境視角下“圓的面積”教學中所蘊涵的數學學科核心素養。

一、剖析生活情境，發展數學建模素養

數學建模聚焦數學學科核心素養的關鍵在于：以生活情境為出發點構建數學模型，經歷“發現、提出、分析、解決問題”的過程，獲得“會用數學眼光看問題、會用數學思維思考問題，會用數學語言表達問題”的能力。

教材中編排的“圓的面積”的內容是簡化的數學建模過程。首先，師生通過剖析生活情境中圓壇（草坪）與鋪圓壇所需的正方形草皮之間的關系，完成圓的面積概念的建構，進而教師提出問題：“如何計算圓的面積？”其次，學生通過操作、觀察、對比等實踐活動完成模型的建立：教師引導學生在硬紙上畫一個圓，把圓對折分成若干等份后剪開，上下拼接剪開后得到小扇形（如圖1），觀察后發現拼出的圖形是近似的平行四邊形（長方形），且隨著分的份數越多，拼出的圖形越接近長方形。再利用長方形的面積公式，建立圓面積S與半徑r之間的函數模型S=π²。最后，通過例1實現模型的應用，即讓學生運用函數模型求解下列問題：若圓壇（草坪）的直徑為20米，每平方米草皮8元，則鋪滿草皮需要多少錢？

剖析生活情境的過程中，學生將體驗如何通過“數學的眼睛”觀察圓壇（草坪），利用“數學的語言”描述和分析圓壇（草坪）的占地面積，最后構建數學問題，即通過建立圓的面積公式這一模型，解決現實生活中與圓的面積有關的具體問題，從而發展學生數學建模素養。

此外，教師可引導學生采用分步法計算例1：第一步，求圓的半徑，20÷2=10（米）;第二步，求圓壇（草坪）面積，3.14×10²=314（平方米）;第三步，求鋪滿草皮所需的金額，314×8=2512（元）。求解的運算程序，可讓學生經歷探究運算思路、選擇運算法則、設計運算程序、求解運算結果的過程，從而發展數學運算素養。

二、借助合情推理，發展邏輯推理素養

邏輯推理素養是依托邏輯推理過程所凝練出來的一種思維品質。圓的面積公式推導可看成邏輯推理的過程，推理的起點是割補轉化法和長方形的面積公式，推理的形式是歸納，得到的推理結果是圓的面積等于無限分割后所拼成的長方形的面積。

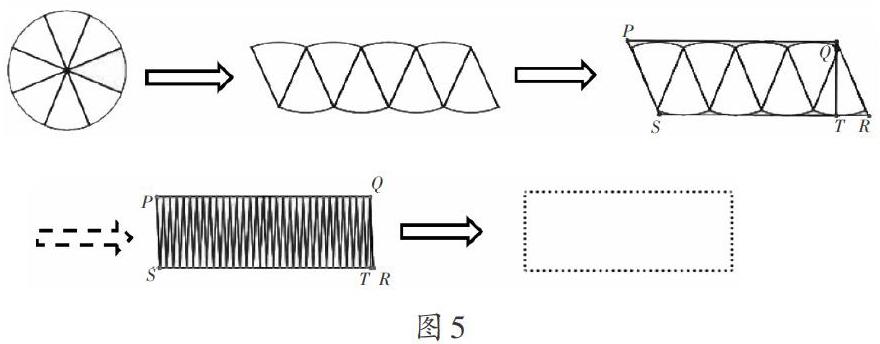
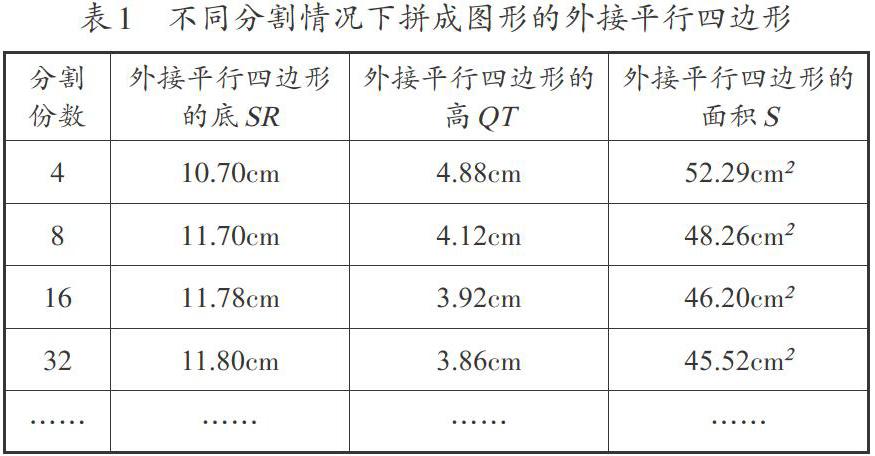
考察分割圓后拼成的圖形及其外接平行四邊形面積的變化情況。利用幾何畫板可得到把任意半徑（文中取3.78cm）的圓等分成4、8、16、32……4×2^n-1（n≥1）后拼成的圖形，以及相應分割下拼成圖形的外接平行四邊形（如圖2）及其底、高和面積之值（見表1）。（此處取π=3.14;記圓的半徑為r，外接平行四邊形的底為SR、高為QT、面積為S;所有數據只保留小數點后兩位）

在用外接平行四邊形面積逼近圓面積的過程中，所拼成圖形的面積（即圓的面積）始終不變，而用于逼近的外接平行四邊形的面積逐漸減小，最后穩定在一個固定的值，即圓的面積。一方面，由圖2知，當等分圓的份數越多，外接平行四邊形的面積越小，最終與所拼成圖形的面積無異。另一方面，隨著分割份數的4份、8份、16份、32份，相應地，外接平行四邊形的底為10.70cm、11.70cm、11.78cm、11.80cm，最終穩定在11.87cm（≈3.14×3.78）附近，外接平行四邊形的高為4.88cm、4.12cm、3.92cm、3.86cm，最終穩定在3.78cm附近，從而外接平行四邊形的面積為52.29cm²、48.26cm²、46.20cm²、45.52cm²，最終穩定在44.86cm²（≈3.14×3.78²）附近。

這一過程基于圓的面積不變，從數形結合的角度，使學生理解把圓無限分割后所拼成的長方形（所拼圖形的外接平行四邊形）的長即圓周長的一半，寬即圓的半徑，且長方形的面積即圓的面積。學生經歷此過程后，將能對合情推理有大致的了解，形成有條理、有邏輯的思維品質，從而發展邏輯推理素養。

此外，利用幾何畫板獲取半徑為3.78cm的圓在不同分割下的外接平行四邊形的底、高和面積之值，并將數據整理制成表1，再分析數據得出結論的過程，亦能讓學生獲得收集、整理數據，并從數據中提取有效信息后做出判斷、得出結論的學習經驗，從而發展數據分析素養。

三、知識可視化，發展直觀想象素養

直觀想象素養是空間想象、幾何直觀和空間觀念相互交融基礎上價值取向的拓展，是數學活動中探索和形成論證思路、進行數學推理、構建數學結構的思維基礎。幾何直觀將相對復雜、抽象的問題圖像化和具體化;空間想象則以現實世界為背景，對事物的幾何表象進行加工、改造，甚至創造新的空間想象。幾何直觀的具體化和空間想象的抽象化使直觀想象素養集具體與想象于一體。

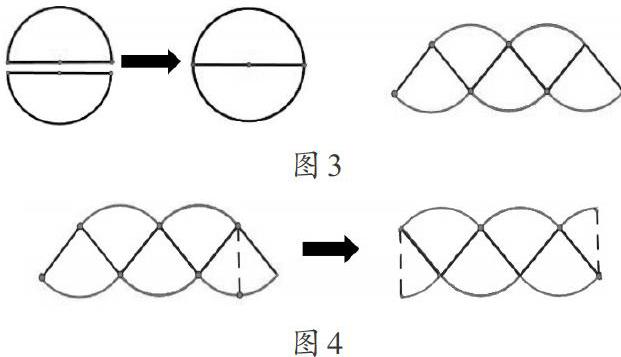
教材編排的“圓的面積”，是通過創設情境，讓學生在生活情境中運用直觀想象抽離出事物的幾何形狀——圓，從而將現實問題轉化為數學問題。公式推導中，借助幾何直觀實現分割拼接的過程：先把圓等分成4個相等的小扇形后剪開，再把每個小扇形對折剪開，接著將圓等分成8份，以此類推。其中，等分圓的份數是4的倍數基于以下兩個原因：一是將圓等分成兩份無操作意義，因為將兩個半圓拼接起來還是圓（如圖3）;二是小學生的認知能力有限，即此前所學的平行四邊形的面積公式推導僅涉及一次割補，因此只考慮將圓割補一次。事實上，若將圓等分成3份，與等分成2份一樣無操作意義。若將圓等分成奇數份（如5份），則只需將其中一個小扇形再對折一次后剪開，拼接到兩側（如圖4），但此時應使用所拼成圖形的外接長方形的面積完成“無限逼近”的過程。

把圓無限分割、拼接、逼近并轉化為長方形的過程中，是借助幾何直觀使復雜的化曲為直過程圖像化、具體化，運用空間想象實現逼近、轉化的思維抽象過程。一方面，隨著分割份數的增加，外接平行四邊形內∠RQT越來越小，斜邊QR越接近于高QT，從而外接平行四邊形越接近于長方形。若將圓無限分割，則外接平行四邊形最終轉化為長方形（如圖5）。另一方面，隨著分割份數的增加，外接平行四邊形的面積越來越小，與所拼成圖形的面積差也越來越小。若將圓無限分割，則外接平行四邊形的面積最終等于所拼成圖形的面積（即圓的面積）。

學生經歷通過幾何圖形實現知識可視化的過程，可增強運用幾何直觀和空間想象思考問題的意識，形成在生活中感悟具體事物本質的數學直觀，從而發展直觀想象素養。

四、結語

事實上，數學抽象素養的發展貫穿整個教學過程。其中，剖析生活情境是從圖形與圖形關系中抽象出數學概念（圓的面積）的過程：基于圓壇（草坪）大小，發現這是與圓（空間形式）和大小（數量關系）有關的普遍性規律，從而抽象出圓的面積的概念。公式推導則是從具體事物中抽象出一般規律和結構，并用數學語言進行表征的過程：回顧平行四邊形、梯形、三角形的面積公式推導過程，啟發學生將圓通過剪拼法轉化為近似的平行四邊形（長方形）后進行研究（如圖1），再基于極限思想，將圓最終轉化為長方形，最后觀察長方形的長與圓的周長、長方形的寬與圓的半徑之間的關系，利用長方形的面積公式抽象出圓的面積與圓的周長、半徑之間的一般規律，并用數學公式S=πr²進行表示。

總而言之，現實情境視角下“圓的面積”教學，可讓學生經歷知識產生以及問題解決的過程，實現學生數學核心素養的發展。同時，數學學科核心素養的發展依托于相應的學習過程，其中，數學抽象是“統領”，數學建模是“大綱”，邏輯推理是“手段”，直觀想象、數學運算、數據分析是“工具”，這六個過程相互交融，形成一個有機整體。

（責編 金鈴）