“分桃”中的分配哲學

呂卉貞

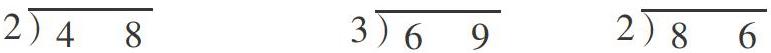
[摘要]“分桃”是北師大版數學教材第五冊第六單元“除法”的第一課時，其設立的教學目標為探究并學會兩（三）位數除以一位數，商仍是兩（三）位數的多位數的除法。教學中，算法流程和算理滲透必須齊頭并進，讓學生能做到嫻熟地計算，且步驟規范、結果準確。不僅如此，教師還要創設具體問題情境，著力培養學生的提問意識，提高學生的解題能力。

[關鍵詞]課前;分析;除法計算;情境;趣味;算理

[中圖分類號]G623.5

[文獻標識碼]A

[文章編號]1007-9068（2020）32-0038-02

“分桃”的教學難點是讓學生依據豎式的格式來參悟算理，并嚴格遵從其書寫的規范格式來列式計算。然而，在實際教學過程中卻事與愿違，有的學生直接一步到位口算出得數，有的學生回到靠擺小棒操作的啟蒙狀態，還有的學生寫出一些怪異的豎式。本文試圖探查滋生這些現象的原因，并探尋出“醫治”的良方。

一、課前分析思考

1.縱覽整本教材，在正式學習豎式前的入門課中，對于這道例題是否應配備練習題，筆者躊躇再三，最終選定了3道簡易練習用以鞏固。其中，例2涉及的知識點是這節課的重頭戲，鑒于學生解題方法應該呈現多樣性和靈活性的原則，是否在練習例1、例2時都用小棒拼擺？經過再三權衡和與同行磋商，最終決定只在做例2時用小棒拼擺。

2.在正式學習豎式時，怎樣向學生灌輸上商時“應先在十位上嘗試，然后再在個位上試商”的原則？如計算48÷2時，一些學生往往不按照常理出牌，先等分個位上的8，再等分十位上的4（也就是40），但這種反常邏輯，有時也會出得出正確的豎式（如圖1）。

為此，在集體備課時，課題組的教師提出了兩種不同的指導意見：一種是直言不諱地指出商應該且必須先商在十位上，而且強制學生必須遵守“從高位到低位依次試商”的原則;另一種是先擱置分歧，直接進入下一題，回頭再來解決。

（1）除法的豎式何故要分層、分格寫成梯級狀？許多學生初次學習這部分內容時，一不留神就走入誤區、迷失方向。因此，教師在講解例1、例2時，一定要著重提醒將被除數等分了幾次、先分配的是哪一部分、后分配的是哪一部分、怎么在豎式中反映出來，要讓學生反復確認，不斷再現推演過程，才能有效防范學生縮減步驟、一次性寫出豎式的錯誤做法。

（2）怎么突破難點？課題組為此展開了激烈辯論。為何不索性讓學生假設自己就是其中一只分桃的小猴，設身處地地思考：你會怎么分配？學生馬上學著小猴的模樣分起桃來：第一步，肯定是先分整籃的桃，有4籃，每只小猴分到1籃;第二步，將剩下的1籃桃和散放的桃合起來再平均分。這樣一來，與講解例1有異曲同工之妙（先分配十位，再分配個位），大大增加了學習的樂趣。

（3）這節課提供的例題雖然只有兩個，但是這兩個例題卻是緊密相連的，不是彼此割裂的，它們之間的邏輯關系是逐級遞進的，要讓學生看清看懂豎式的推展過程是先分十位，再分個位，使學生的印象不斷加深。

3.這節課的重心落在例2上。教師講解例2時需要精講細說，因此講解例1的用時不宜太長，要長話短說、簡明扼要，但要語言明暢通達，尤其是提問時，要切記抓住關鍵，不要主次不分。

二、課中的實踐嘗試

1.例1的課堂實錄

師：你讀取了哪些有用的數學信息？

生1：一共有2只小猴，48個桃。

師：你認為怎樣分配才公平公正？

生1：平均分，每只小猴分到的桃一樣多。

師：誰能設計一個問題，要求解答時必須用除法解決？

生2：48個桃平均分給2只小猴，每只小猴分到幾個桃？

（教師將這個問題板書，呈現時，務必著重突出“平均”這個關鍵詞）

師：那你說說到底該怎么列式呢？

生2：48÷2。

師：你的計算思路是什么？

生3：我是采用口算的辦法，先口算40÷2=20，再口算8÷2=4，最后將兩個商加起來，即20+4=24，于是推知48÷2=24。

師：如果你是一只急于吃到桃的小猴，想快點分到桃，你打算怎么分配？

生4：先分給每只小猴2籃桃，再給每只小猴補分4個桃，這樣一來，每只小猴就分到24個桃。

生5：先給每只小猴分4個桃，然后再給每只小猴補分2籃桃，這樣一來，每只小猴也分到24個桃。

師：現在假設你就是其中一只小猴，按照你的思路，你會先取整籃的桃，還是先取散放的桃？

生（齊）：先取整籃的桃。

師：那我們前后一共分了幾次桃？

生（齊）：兩次。

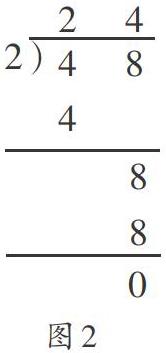
師：列出豎式會是什么形式？（板書如圖2）

解決這道題的方法呈現多樣性，具體如下：（1）口算;（2）擺小棒，分一分;（3）豎式計算，但在豎式計算中一定會錯漏百出。

以上教學過程中，教師增加了課堂的趣味性，幫學生重新整理思路。“現在假設你就是其中一只小猴，按照你的思路，你會先取整籃的桃，還是先取散放的桃？”將分配的過程落實到細節上，將分配的經過分成不同的程序，讓學生清清楚楚地感知到，是先分十位（整籃的桃），再分個位（散放的桃），而這是在豎式計算中不能展示的分配過程。向學生追問“那我們前后一共分了幾次桃？”，再次重申和強調分的流程是分階段的，然后對照豎式的格式，讓學生從豎式中探查到兩次分配的痕跡。由此看來，這句追問必不可少。

隨后，教師出示練習，學生上臺板演展示。

這是不可或缺的步驟，趁熱打鐵進行訓練，可以鞏固學生對除法豎式算理的理解，加深印象，這幾個豎式計算時都要分步展開，使學生的印象更加深刻，為接下來的學習打好基礎。

2.例2的課堂實錄

師：現在又加入一只小猴，桃的總數不變，怎么分才公平？你能設計出一個用除法解決的問題嗎？

生6：有48個桃，平均分給3只小猴，每只小猴分到多少個？

（教師將這個問題板書）

師：該怎樣列式？

生7：48÷3。

師：請大家借助桌上的小棒擺一擺、分一分，再寫出豎式。

（學生反饋的信息顯示，一般分的始末都能交代清楚）

師：前后一共分了幾次？先分配的是哪一部分？后分配的是哪一部分？

生8：前后一共分配兩次，先分的是十位上的數字，后分的是個位上的數字。

教師在教學例1時棄用了擺小棒的方法，目的是把重心轉移到例2上，讓學生自行研究、開發算法。通過自身實踐得到的經驗和結論，學生的印象會更加深刻，再加上教師的指引和提點，就能夠讓學生牢固掌握兩（三）位數除以一位數的豎式計算的方法，并諳熟算理。

3.小結

師：觀察黑板上的豎式，分辨一下它們都是從什么數位開始試商的？

生9：從最高位十位開始。

師：每次相除所得的商值對齊到哪個數位上？

生10：先拿被除數十位上的數對除數做除法運算，所得的一位數商對齊到被除數十位位置橫線上方，再拿被除數個位上的數對除數做除法運算，所得的一位數商對齊到被除數個位位置橫線上方。

4.練習鞏固

教師增設了一個小結的環節，將被除數由兩位數擴增至三位數，加強學生對所學知識的靈活運用能力和應變能力。

豎式的格式是一定的，是不容篡改和歪曲的，但是規定這樣的格式卻不是由誰的個人意志決定的，也不是由誰的個人習慣決定的，而是由多位數除以一位數的算理促成的，必須從高位開始依次除到低位。小猴分桃的情境恰好直觀地揭示出這一算理，先分整籃的桃，再分散放的桃，因為散放的桃要一個一個拿，不好分。這也正應和了先易后難的思維習慣。

（責編 李琪琦）