高超聲速飛行器保預設性能的反演控制方法*

李小兵，趙思源，卜祥偉，何陽光

(1. 空軍工程大學 防空反導學院， 陜西 西安 710051； 2. 空軍工程大學 研究生院， 陜西 西安 710051)

高超聲速飛行器(Hypersonic Flight Vehicles，HFV)作為一種新型的臨近空間戰略武器裝備，已成為近十年來的研究熱點。控制系統面臨著系統的不確定性、復雜子系統與非線性模型的耦合，因此HFV的飛行控制器設計成為一個具有挑戰性的研究課題[1-3]。同時，由于系統的不確定性，控制增益信號一般是未知的，給控制器的設計帶來了很多困難[4-5]。傳統的仿射模型控制器設計方法不能處理HFV非仿射模型，對控制器的動態性能和穩態精度提出了更高的要求[6-8]。

HFV在大跨度飛行包絡范圍內需要完成許多復雜的任務，因此有必要設計一種有效的控制方法。然而，復雜的飛行環境、未知的外部干擾和模型的不確定性使得HFV的魯棒控制具有挑戰性[9-11]。為了解決HFV飛行過程中的不確定項和干擾問題，文獻[12]并沒有使用動態高階微分器，而是設計了一種無模型跟蹤控制器。文獻[13]研究了HFV縱向運動模型的魯棒控制，保證了對模型不確定性的魯棒控制律。為了克服魯棒控制通常過于保守的缺點，文獻[14]設計了一種適用于HFV的滑模控制律。當模型參數受到擾動時，控制律仍能保證參考輸入的穩定跟蹤。文獻[15]研究了高階連續滑模控制器的設計，實現了HFV控制輸入的連續切換，避免了控制輸入高頻抖振的影響。在文獻[16-17]中，HFV容錯控制是為了保證執行器故障的穩定跟蹤而設計的。文獻[18]介紹了最小學習參數算法，估計了神經網絡權值矩陣的范數，降低了在線學習量。文獻[19]對模型進行了變換，將HFV模型分解為速度子系統和高度子系統，將高度子系統轉化為等效的純反饋系統，避免了傳統反演方法的缺點，引入了最小參數學習方法，減小了計算量。

國內外對HFV仿射控制的研究雖取得了很大的成果，但實際模型是非仿射的，且不宜被仿射化。由于上述控制策略只保證了控制系統的穩態性能，因此不考慮系統的動態性能。并且，對HFV高速飛行和控制系統快速飛行的動態性能要求也不能滿足。文獻[6] 設計了HFV預設性能反演控制器，因為控制律對預設性能函數的初值選擇提出了更高的要求，雖然速度和高度跟蹤誤差限制在預設范圍內，但可用性和實時性較差。在文獻[20]中，通過組合隱藏函數和均值定理，對仿射模型進行了變換，并通過RBF神經網絡對未知函數進行了逼近，提出了一種自適應變結構控制的非仿射控制方法。文獻[21]通過泰勒公式將HFV非仿射模型轉化為仿射模型，設計了自適應模糊神經非仿射控制律。本文利用中值定理[22]對HFV的非仿射模型進行變換，然后利用神經網絡估計未知函數，同時引入Nussbaum函數來處理以前未知的控制方向問題。

本文設計了一種新型HFV縱向運動跟蹤控制器，該控制器是基于HFV非仿射模型提出的保證預設性能的反演控制策略，旨在保證跟蹤誤差被限定在預設區域內。控制器的設計是建立在非仿射模型上的，這避免了模型簡化過程中的不確定并保證了控制策略的可行性。所設計的預設性能控制器實現了準確地對參考輸入的穩定跟蹤。由于控制策略的建立與準確的飛行器模型和函數估計值無關，因此增強了系統魯棒性的同時降低了在線計算量。最后，通過仿真實驗驗證了控制策略的實用性和優越性。

1 問題描述

1.1 HFV縱向平面運動學方程

本文采用Bolender和Parker的HFV面向控制的非線性模型[23-24]，其縱向平面受力情況圖1所示。HFV上所受的空氣動力可以表示為升力L、推力T、阻力D和俯仰力矩M，推力T作用在飛行器機體軸線上。同時，圖1也表示了HFV的航行速度V，航行高度h，航跡角γ，俯仰角θ，攻角α=θ-γ。由標準拉格朗日方程推導出的HFV縱向動力學模型可以表示為如下形式：

(1)

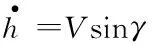
(2)

(3)

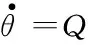
(4)

(5)

(6)

(7)

其中，部分系數表達式如下：

(8)

L、T、D、M只表示力的大小，其擬合式如下：

(9)

(10)

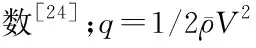
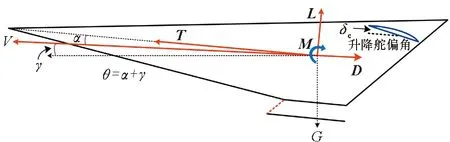
圖1 HFV受力示意圖Fig.1 Force map of HFV model

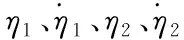
HFV巡航段飛行速度V的變化相對于俯仰角θ和俯仰角速率Q近似為慢變量[9]，為了便于設計控制器，通常將HFV模型分解為速度子系統(見式(1))和高度子系統(見式(2)～(5))，并分別進行控制器設計。

假設1所有的參考指令和它對于時間的一階及二階導數是有界連續的。

1.2 預設性能分析

定義連續函數ρ(t):R+→R+，若同時滿足以下兩個條件[25]，則該連續函數可被稱為預設性能函數。

1)ρ(t)是嚴格單調遞減的正函數；

基于上述定義，本文設計如下預設性能函數：

ρ(t)=(ρ0-ρ∞)e-lt+ρ∞

(11)

其中，ρ∞≤ρ(t)≤ρ0，ρ0>ρ∞>0，l>0為待設計參數。

跟蹤誤差e(t)需要滿足下述定義不等式：

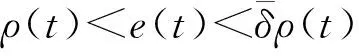
(12)

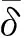
這就保證e(t)具有滿意的動態性能與穩態精度，且ρ(t)是有界的。在設計控制系統的過程中，直接對不等式約束式(12)進行處理的難度非常大，因此可以先將不等式約束轉化為等式約束再進行設計，這里定義一個誤差轉換函數S(ε(t))，則

(13)

將S(ε(t))選取為如下形式：

(14)

顯然，S(ε(t))具有嚴格遞增性，于是其逆函數ε(t)的一階動態方程為：

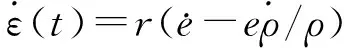
(15)

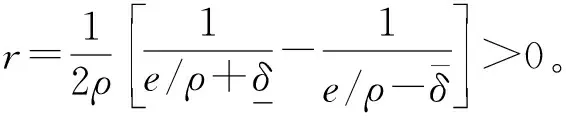
(16)

(17)

1.3 RBF神經網絡

引入如下徑向基函數(Radial Basis Function, RBF)神經網絡用來逼近模型不確定項：

φ(Z)=WTS(Z)

(18)

式中，φ∈R和Z∈Rn分別是神經網絡的輸出和輸入，W∈Rn為權值向量，S(Z)=[S1(Z),…,Sn(Z)]T是徑向基函數。通常情況下，將Si(Z)選取成如下高斯基函數：

(19)

式中，ai∈Rn為高斯基函數中心向量大小，bi∈R+為高斯基函數的寬度。

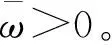
φ(Z)=W*TS(Z)+Δ(Z)

(20)

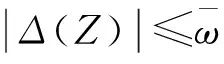
(21)

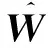
2 控制器設計與穩定性分析

2.1 指令濾波器

當采用反演控制方法設計控制器時，“微分項爆炸問題”必然會發生。本文將引入一組指令濾波器，而不是反復求導[26]。其表達形式如下：

(22)

其中，ηω>0為待設計參數，δi-1為虛擬控制信號。

定義估計誤差信號?i為如下形式：

?i=ωi-δi-1,i=2,3,…,n

(23)

則

(24)

zi=xi-δi-1,i=2,3,…,n

(25)

式中，xi為實際信號，在后文的設計中i代表HFV縱向模型中的γ,θ,Q。

2.2 速度控制器設計與穩定性分析

由于速度的動態變化比高度系統慢，所以當速度變化時，可以認為高度和高度角已經達到了其穩定狀態[4]。因此將速度子系統表達式寫為如下形式：

(26)

式中，fV是未知的不可微非仿射連續函數，Φ和V為速度子系統的輸入和輸出。根據中值定理，將式(26)改寫為如下形式：

(27)

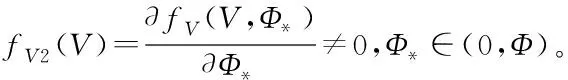
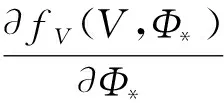
ρV(t)=(ρV0-ρV∞)e-lVt+ρV∞

(28)

根據式(12)可以得到：

(29)

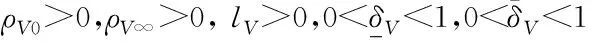
將式(29)轉化為：

(30)

綜合式(17)和式(27)，將轉換函數zV(t)對時間求導可得：

(31)

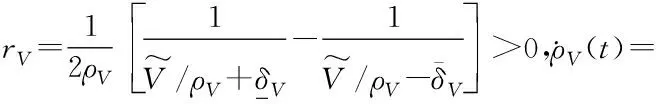
定義Lyapunov函數為：

(32)

式中，νV為動態信號，λV0為待設計參數。對式(32)求導可得：

(33)

根據Young′s不等式以及假設2，有

(34)

將式(34)代入式(35)，可得：

(35)

令

(36)

由于μV0(V)是非負的連續函數，則必存在一個連續的函數φV(ZV)，使得

zVφV≤zVφV(ZV)+λV

(37)

其中，ZV=[V,zV,rV]T∈R3，λV>0為待設計參數。

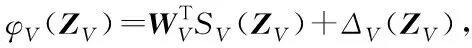
將速度控制律Φ設計為：

(39)

選取如下Lyapunov函數：

(40)

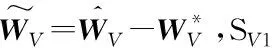
對式(40)求導可得：

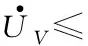
(41)

由于

(42)

則式(41)可進一步寫成

(43)

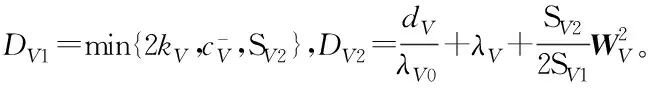
(44)

2.3 高度控制器設計與穩定性分析

為了便于控制器設計，根據式(2)～(5)將HFV高度子系統改寫為如下形式：

(45)

其中，fh、fγ、fθ和fQ是未知的不可微非仿射連續函數。根據中值定理將式(45)改寫為：

(46)

假設4參考指令href和它對于時間的一階及二階導數是有界連續的。

ρh(t)=(ρh0-ρh∞)e-lht+ρh∞

(47)

根據式(12)可以得到

(48)

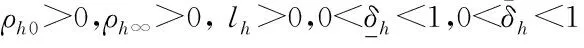
將式(48)轉化為：

(49)

綜合式(17)和式(46)，將轉換函數zh(t)對時間求導可得：

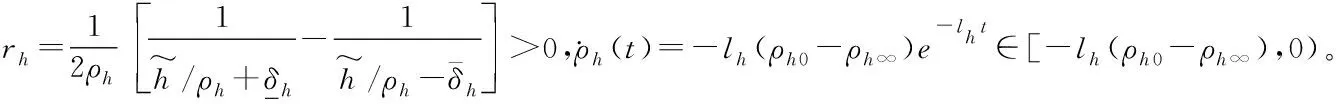
定義Lyapunov函數

(51)

式中，νh為動態信號，λh0為待設計參數。對上式求導可得：

(52)

根據Young′s不等式及假設3，有

(53)

將式(53)代入式(52)，可得：

(54)

令

(55)

由于μh0(h)是非負的連續函數，則必存在一個連續的函數φh(Zh)，使得

zhφh≤zhφh(Zh)+λh

(56)

其中，Zh=[h,zh,rh]T∈R3，λh>0為待設計參數。

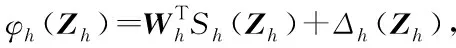
將虛擬控制律γd設計為：

(58)

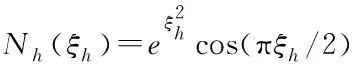
選取如下Lyapunov函數

(59)

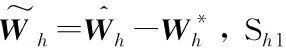
對式(59)求導可得：

(60)

由于

(61)

則式(60)可進一步寫成

(62)

(63)

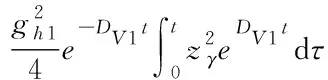
考慮系統式(46)，結合指令濾波器，可得：

zγ=γ-γd=γ-ωγ+?γ

(64)

進一步，有

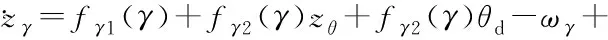
(65)

定義Lyapunov函數

(66)

對上式求導可得：

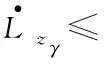
(67)

類似于速度控制器設計，可以得到

(68)

令

φγ=fγ1(γ)+ηω(ωγ-γd)

(69)

存在一個未知的連續函數φλ(Zλ)，使得：

(70)

其中，Zγ=[γ,zγ,ωγ,γd]T∈R4，λγ為待設計參數。

將式(70)代入式(68)，可得：

(71)

將虛擬控制律θd設計為：

(72)

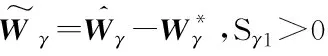
選取如下Lyapunov函數

(73)

對上式求導，并綜合考慮Uh和Lzγ可得：

(74)

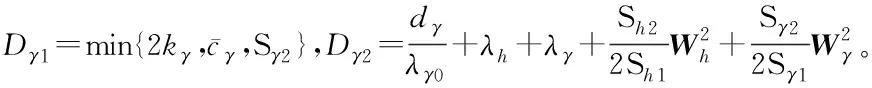
對式(74)兩邊同乘e-Dγ1t并積分，可得：

(75)

虛擬控制律Qd的設計過程及穩定性證明均和以上步驟類似，這里不再贅述。 直接給出將虛擬控制律Qd設計為如下形式：

(76)

考慮系統式(46)，結合指令濾波器，可得：

zQ=Q-Qd=Q-ωQ+?Q

(77)

進一步，有

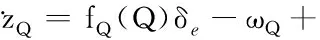
(78)

定義Lyapunov函數

(79)

對上式求導可得：

(80)

令

φQ=ηω(ωQ-θd)

(81)

存在一個未知的連續函數φQ(ZQ)，使得：

(82)

將實際控制律δe設計為：

(83)

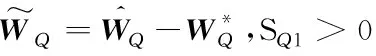
選取如下Lyapunov函數

(84)

對上式求導，并綜合考慮Uθ和LzQ可得：

(85)

對式(85)兩邊同乘e-DQ1t并積分，可得：

(86)

(87)

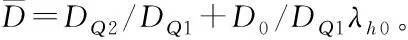
3 仿真與分析

針對HFV動力學模型進行速度與高度的閉環仿真實驗。速度與高度參考輸入均由圖3所示的二階參考模型給出。該二階參考模型的傳遞函數為[27]：

(88)

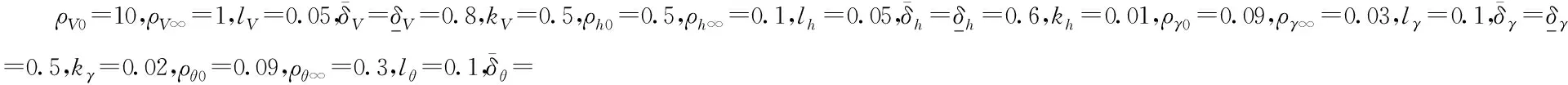
HFV飛行包線的剛體取值范圍可以見文獻[28]。 仿真中，HFV的初始狀態取值見表1。

通過MATLAB/Simulink搭建控制系統，采用步長為0.01 s的四階Runge-Kuta法進行驗證控制方法的有效性。要求臨近空間巡航階段HFV在速度階躍Vd=100 m/s,高度階躍hd=100 m作用下。控制任務是要求系統輸出能夠準確跟蹤給定的速度和高度參考指令并保證跟蹤誤差穩定在預設的區域內。為了檢驗控制律的魯棒性，仿真中給HFV模型氣動系數存在±40%的攝動量，定義：

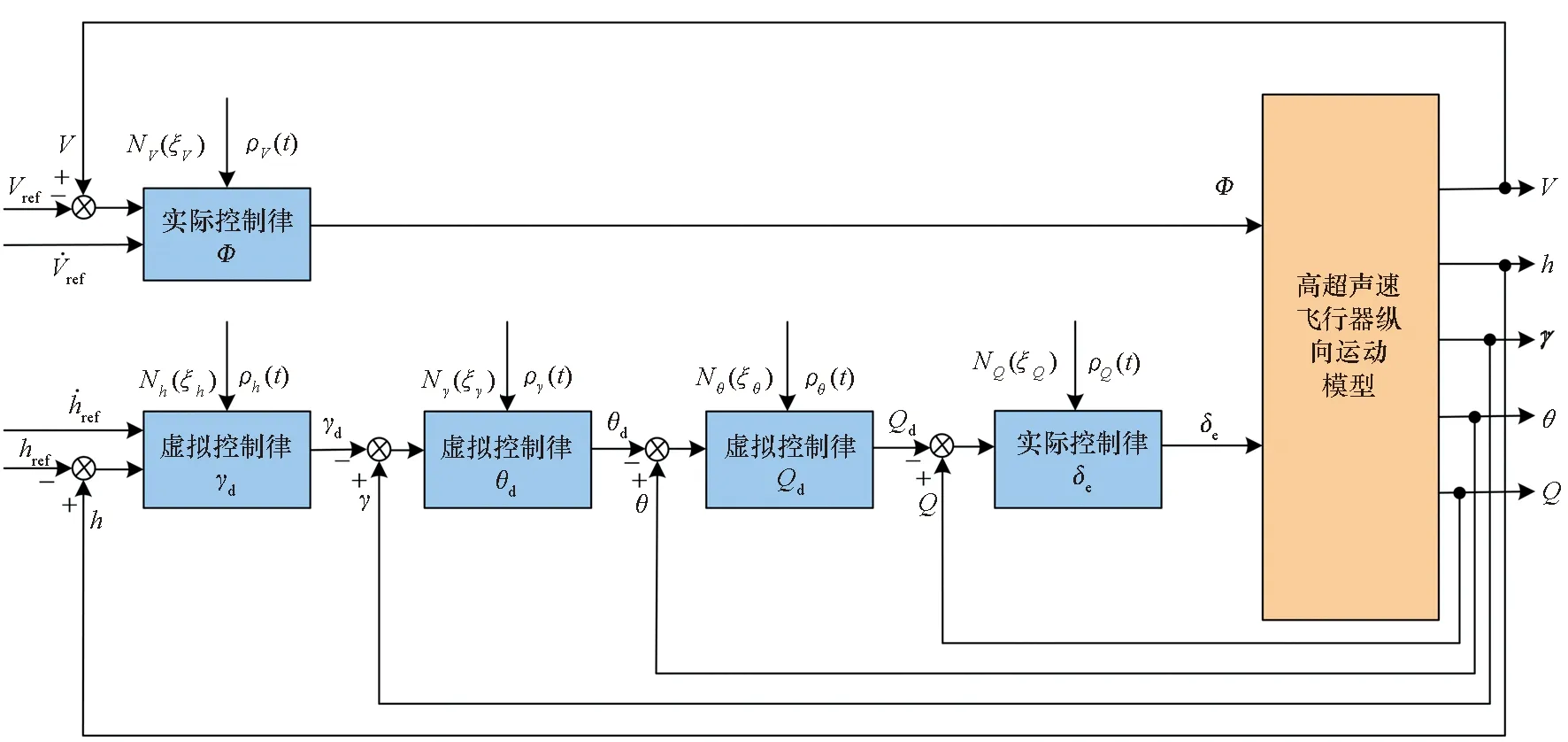
圖2 HFV控制結構圖Fig.2 Control structure of HFV

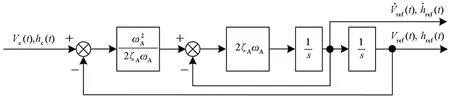
圖3 參考輸入二階模型結構Fig.3 Second-order model structure of reference

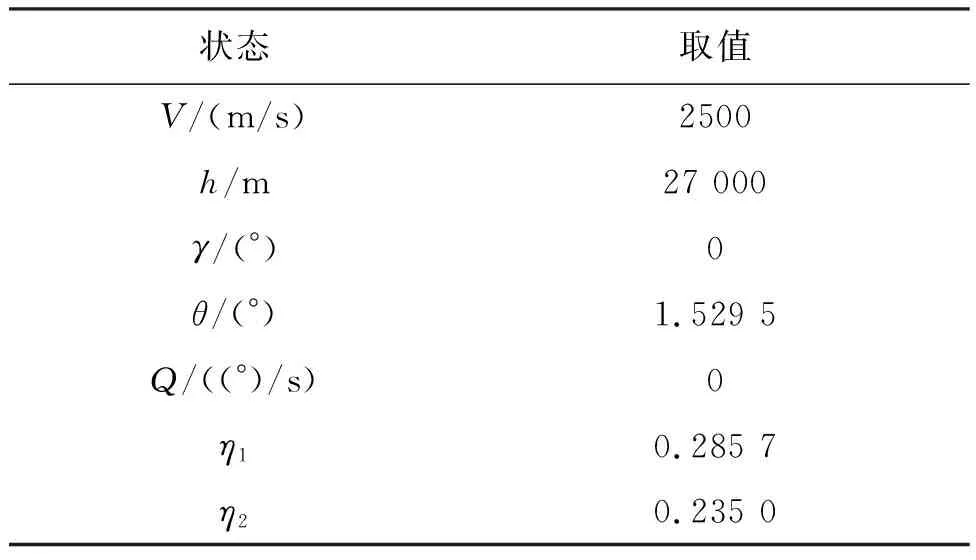
表1 HFV的狀態初值

(89)

式中，C0表示HFV氣動系數的標稱值。

為了驗證本文所提方法具有更好的使用價值，將保預設性能(Guarantee Prescribed Performance, GPP)方法與文獻[29]中神經反演控制(Neural Network Backstepping, NNB)方法進行對比仿真，仿真結果如圖4～9所示。在模型參數攝動的情況下，本文設計的GPP方法能保證速度跟蹤誤差和高度跟蹤誤差的穩態精度和較好的動態性能，實現速度跟蹤誤差的小超調收斂和高度跟蹤誤差的零超調收斂。由圖4～5可知，與文獻[29]中的NBB方法相比，該控制器的速度和高度跟蹤誤差能更快地收斂到零，這表明該控制器比文獻[29]中的NBB方法具有更好的動態性能；圖6～9顯示了兩個控制器的姿態角、彈性狀態和系統輸入都是平滑的，沒有高頻抖振。如此，設計的控制器可以保證速度跟蹤誤差的小超調收斂和高度跟蹤誤差的零超調收斂。同時，控制律對參數的存在具有魯棒性，控制系統的動態性能和穩態精度滿足預定性能的要求。

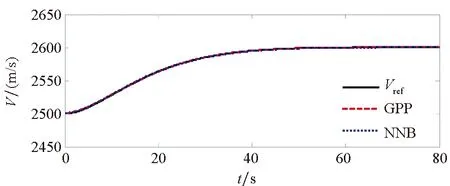
(a) 速度跟蹤曲線(a) Velocity tracking curve

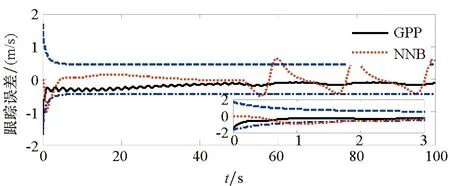
(b) 速度跟蹤誤差(b) Velocity tracking error圖4 速度跟蹤響應Fig.4 Velocity tracking performance

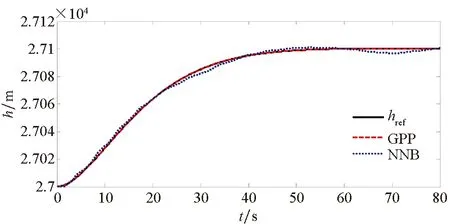
(a) 高度跟蹤曲線(a) Altitude tracking curve

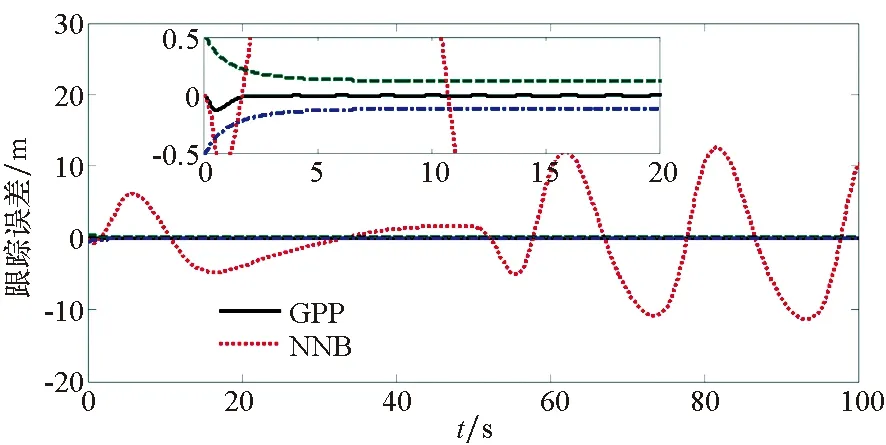
(b) 高度跟蹤誤差(b) Altitude tracking error圖5 高度跟蹤響應Fig.5 Altitude tracking performance

(a) 航跡角曲線(a) Path angle curve

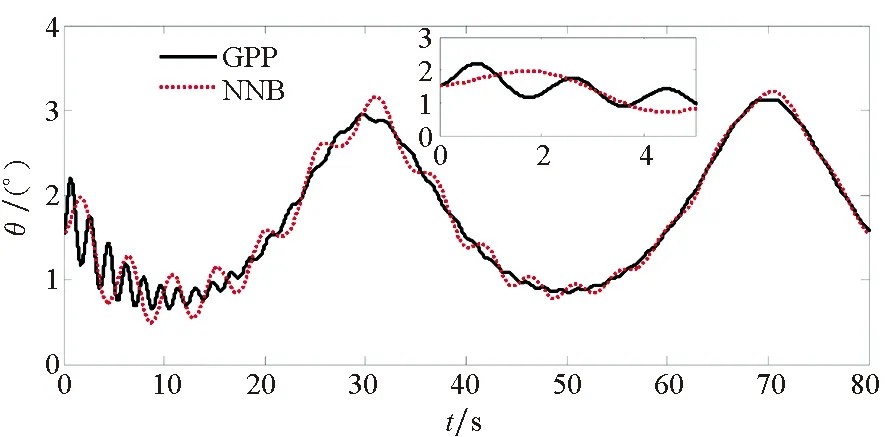
(b) 俯仰角曲線(b) Pitch angle curve

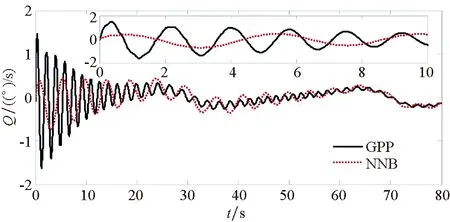
(c) 俯仰角速度曲線(c) Pitch rate curve圖6 高度角曲線Fig.6 Altitude angle curve

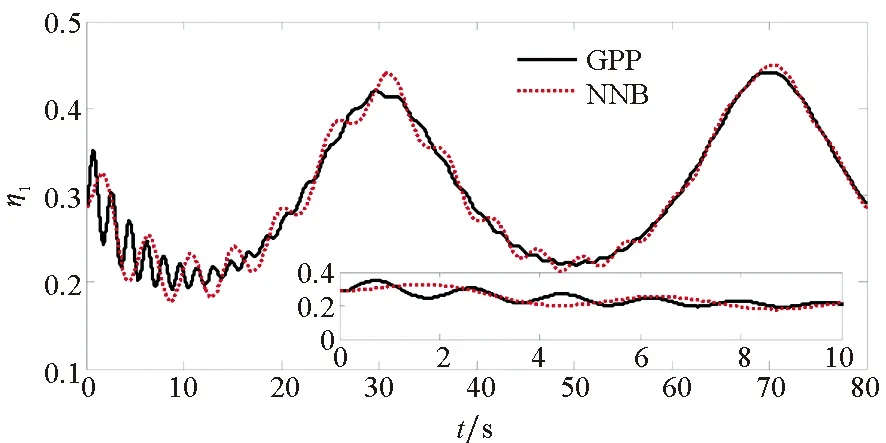
(a) 第一彈性狀態(a) The first flexible state

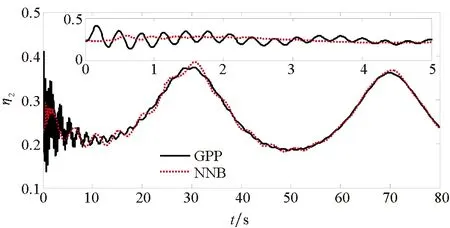
(b) 第二彈性狀態(b) The second flexible state圖7 彈性狀態Fig.7 The flexible states

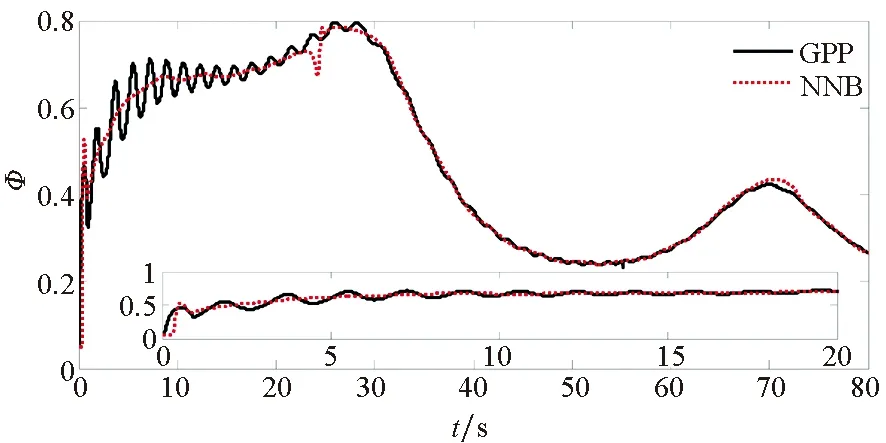
圖8 燃料空氣比Fig.8 Flue-to-air ratio

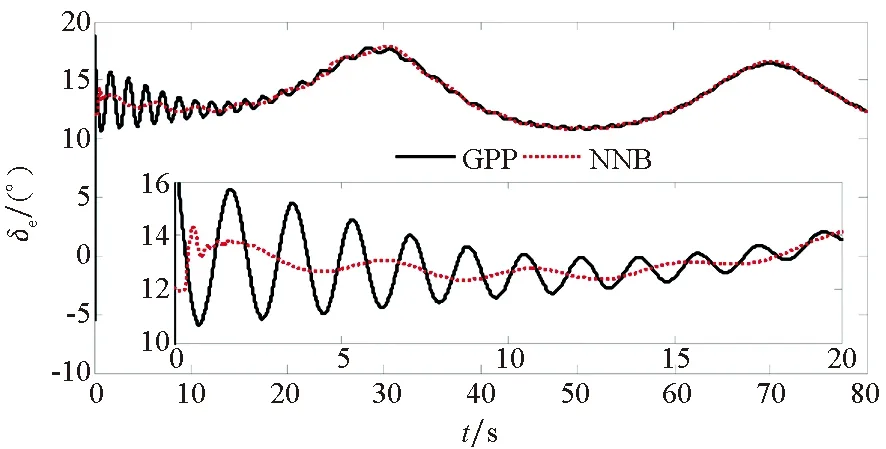
圖9 升降舵偏角Fig.9 Elevator declination

4 結論

本文在反演控制方法的結構下，為HFV設計了一種保證預設性能的控制方法。通過引入預設性能函數來限定跟蹤誤差的預設范圍，控制律的設計基于HFV的非仿射模型，保證了預期的動態性能。所設計的控制器不再需要精確的模型以及控制增益的信號，其魯棒性和實用性得到了很大的提升。通過引入動態信號，克服了原模型中存在未建模的動態，并引入一組指令濾波器，有效地規避了反演控制方法中的反復求導，運用Lyapunov方法證明了所有閉環系統的穩定性。最后，數字仿真結果表明了所設計的控制器對參考信號跟蹤的準確性及較好的可行性。