Volterra級數模型的非線性壓縮測量辨識算法*

邱 棚，姚旭日，李鳴謙，翟光杰

(1. 中國科學院國家空間科學中心， 北京 100190； 2. 中國科學院大學， 北京 100049)

一直以來，關于非線性系統的研究吸引了來自各個領域學者的關注。特別是在工程領域中，理想的線性系統是幾乎不存在的，大部分需要面對的都是非線性系統。一般認為，輸出與輸入不成比例的系統均是非線性的，如失真、自激振蕩、分叉、混沌等。本文重點研究弱非線性系統，比如功率放大器[1]、揚聲器[2]、生物過程[3]均屬此類。對于此類非線性系統，其模型是很難通過理論推導得到的。因而，需要通過對輸入輸出信號的辨識得到系統模型。

在系統辨識中，首要考慮的問題是如何表示非線性系統。到目前為止，還沒有一個通用的非線性系統表示方法。非線性系統的模型可以從以下幾個方式來獲得：獲得系統的頻域等價模型；將非線性環節表示為多個線性環節的卷積；將非線性系統展開為線性形式，再利用線性的辨識方法獲得非線性系統的近似等。本文采用后一種方法，利用多項式展開的方法來表示非線性對象。根據泰勒公式可知，如果系統的非線性環節足夠平滑并且沒有歷史記憶，那么就可將系統的輸出表示為輸入信號的多項式展開。但是，如果系統是有記憶的，就需要用Volterra級數來描述[4]。本文選用p階、記憶長度為L的Volterra核作為基礎，并利用多項式回歸的方法得到核的參數，從而使得展開項的和盡可能地接近原函數。近年來，Volterra級數以及其他多項式展開的方式在人臉識別[5]、語音識別[6]、文字識別[7]等非線性問題上都取得了成功。

系統辨識的第二個問題是如何準確估計出模型中的參數。鑒于Volterra級數中的未知參數可以表示為輸入輸出的線性組合，經典的最小二乘(Least-Square，LS)方法就可辨識得到[8]。但是，此方法會碰到“維數災難”的問題，即待辨識的參數數量將隨著模型階數的增加而呈指數增長。對于LS方法而言，就需要遠大于Θ(Lp)次的數據，辨識結果才能收斂。這不僅增加了辨識的成本，還會增大計算復雜度。一個可能的方法是，將該問題視為核回歸問題[9-10]。然而，Volterra級數的高階參數是稀疏度的，也就是說待辨識參數中只有個別位置是非零的。不過，多項式的階數、記憶長度以及非零項的位置和個數都是未知的，所以無法在辨識之前選定合適的數值。此外，在實際系統中，核回歸的方法由于輸入輸出數據存在誤差將導致過擬合，使得辨識結果變差。考慮到參數的稀疏性，有學者提出采用稀疏估計器來解決過擬合的問題，典型的如非負參數推斷(Non-Negative Garrote, NNG)[11]和遞歸最小二乘(Recursive Least Squares,RLS)估計器。文獻[18]給出了針對稀疏Volterra級數的EM-RLS算法，對參數的期望和分布進行計算，從而得到準確的辨識結果。另一個常見的稀疏估計器叫作最小絕對收縮和選擇算子(Least-Absolute Shrinkage and Selection Operator, LASSO)[13]。文獻[14]基于該算法，提出了針對Volterra級數的wLASSO(weight LASSO)估計器，并取得了良好的效果，而且wLASSO的性能已經在文獻[15]之中分析過了。除了利用稀疏性解決“維數災難”問題的方法以外，還有利用核的對稱性以減少待辨識參數的個數[8]。另外，還可以利用正交三角分解的方法來減少辨識計算量[16]。

近年來，Donoho[17]、Candès等[18]提出的壓縮感知理論是處理信號稀疏性的一種高效方法。根據采樣定理可知，對任何信號的測量都要求采樣頻率是信號帶寬的2倍以上。然而，壓縮感知理論指出，對稀疏信號的測量需要關注的是稀疏度，而不是信號帶寬。該定理目前已經被大量應用于有關成像的各個領域中，如高速流顯微鏡成像[19]、核磁共振成像[20]、合成孔徑雷達[21]、毫米波雷達信號處理[22]等。Volterra級數中的一階核可以視為一維的信號，其二階核也可視為二維的信號。依此類推，級數的各階核參數均可以視作高維信號，而且這些信號均是極度稀疏的。因而，利用壓縮感知理論，可以極大地提高測量的效率。

1 多項式級數展開

本節主要介紹非線性系統的Volterra級數展開方式。假設一個離散非線性時不變系統的輸出可表示為：

y(n)=f(x(n),x(n-1),…,x(n-l))

(1)

其中，x(n)代表系統在時刻n的輸入，而f(x)則是一個非線性函數。上式表示，系統的輸出與當前時刻之前的所有時刻都相關，即系統是有無限記憶的。但是，對于大部分系統而言，系統的響應都會隨著時間的推移而衰減。所以，在此假設系統的記憶是有限且合理的，也就是系統的輸出只與前L個時刻的輸入有關。本文只考慮由死區、飽和、諧波等導致的信號失真等弱非線性系統。理論上，Volterra級數是一個無窮級數，而本文允許展開級數與原系統存在截斷誤差，所以系統的輸出就可以利用P階的Volterra級數來表示：

(2)

式中：v(n)包含截斷誤差以及測量噪聲，而且該噪聲是一個零均值并且獨立于輸入信號的白噪聲；Hp[Χ1(n)]表示第p階的Volterra核，其具體形式如下:

(3)

式中，L代表Volterra級數的記憶長度，而且各階核的記憶長度是一致的。針對Volterra級數展開的收斂域以及使用范圍已經被廣泛研究，可以參考文獻[8]。本文的目的是利用系統的輸入輸出數據，以辨識得到可以準確描述系統的各階核參數hp(k1,…,kp)。

2 非線性壓縮測量辨識

非線性壓縮測量辨識算法將壓縮感知理論引入對非線性系統的辨識之中，并利用測量的方法對模型參數進行觀測。在測量的框架下，首先要確定被測信號的形式。在系統辨識中，被測信號包含了系統的全部特征，每一個信號都可以唯一地表示一個系統。對于線性系統來說，可以選擇系統的脈沖響應序列來表示，該信號包含了線性系統的全部動態和靜態特征。那么，對于非線性系統來說，是否存在一個信號是可以唯一地表達系統的呢？本文采用Volterra級數的各階核來表示。另外，在測量的角度下，可以認為表示系統的信號是客觀存在的，只不過需要特殊的觀測方法才能夠得到，或者是需要通過間接的方法來對其測量。本文的重點在于介紹測量在辨識非線性系統中的思想，因而只考慮二階Volterra級數的辨識問題，而更高階系統可以依此推廣。由于忽略了高階核，所以測量結果與原信號存在一定偏差，而這個偏差從測量的角度來看，是由于測量工具的局限性導致的。這就如同用米尺去測量毫米級的物體一般，一定會存在誤差。

假設非線性系統展開為二階Volterra級數，該系統輸出可以表示為：

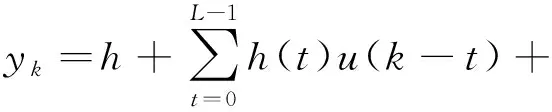
(4)

根據上文對Volterra級數的介紹可知，一個非線性系統的輸出可以寫為多維卷積的形式。對于一階Volterra核，可以將一維卷積改寫為向量相乘的形式，即：

(5)

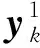
(6)

根據式(2)可知，二階Volterra核的輸出可以寫為線性二次型的形式，即：

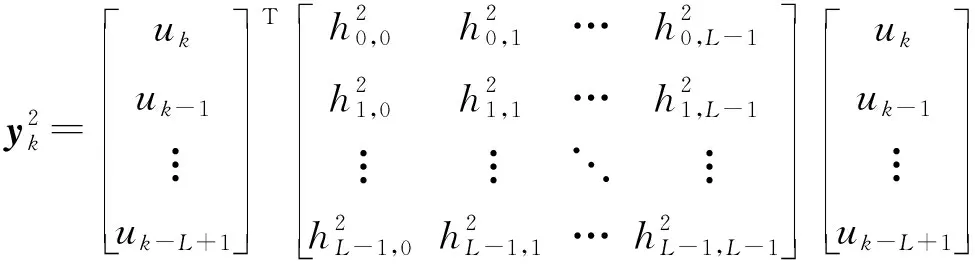
(7)

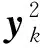
(8)

此時，將一階核和二階核先后排列成一個一維列向量，那么非線性系統輸出可以表示為：

Y=Y(0)+Y(1)+Y(2)=[U(0),U(1),U(2)][Hc,H1,H2]T

(9)

式中，U(0)是一個M×1的常數向量，Hc是一個1×1 的常數向量。H=[Hc,H1,H2]T是待測量信號，該信號長度N=L2+L。不過，由于二階核是關于對角線對稱的，因此可以將相同項合并，即信號長度縮減為N=(L2+3L+2)/2；U=[U(0),U(1),U(2)]是測量矩陣，該矩陣中的每一行都是一個測量向量，用于對信號H進行一次觀測。因而，矩陣U的性質直接決定了測量的準確性。壓縮感知理論給出了準確測量的要求，即只有當測量矩陣滿足有限等距約束(Restricted Isometry Property, RIP)性質時，才能保證測量是無損的。學者已經證明一般常見的獨立同分布的隨機矩陣都滿足RIP性質。不過，對于本文中使用的復雜隨機矩陣，要想得到RIP性質的充要條件是十分困難的。因而，可以通過證明得到滿足RIP性質的充分條件來得到對測量矩陣的要求。文獻[23]中給出了當輸入信號是符合均勻分布的隨機信號時的定理如下：

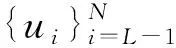
該引理表明，當利用符合均勻分布的測量矩陣對信號進行測量時，如果測量數是與S2lgN在同階大小時，恢復算法是有極大的概率從觀測值中重建出被測信號的。不過，此處只是給出了均勻分布的測量準則，而且該準則只是給出了一個相對寬泛的下限。此外，如果系統輸入選取的是其他隨機分布，就需要重新推導RIP定理。因而，本文嘗試間接地給出測量矩陣需要滿足的性質。根據RIP定理的定義可知，RIP性質描述的是從測量矩陣中任意抽取任意列組成的子矩陣能否完整地保存原信號的能量，即不對原信號過分放大也不過分衰減。因而，測量矩陣的子矩陣滿足RIP性質是一個必要條件。利用圓盤定理來解釋，可以認為RIP性質要求測量矩陣的Grammian矩陣R=UTU的特征值在[1-δS,1+δS]范圍內。概括來說，要想保證測量是準確，就需要滿足以下三個條件：

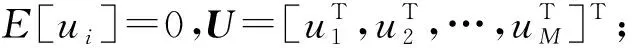
②E[Ri,i]=1,i=1,…,N；

③E[Ri,j]=1,i,j=1,…,N,i≠j。

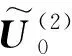
其中

(10)

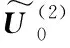
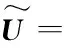
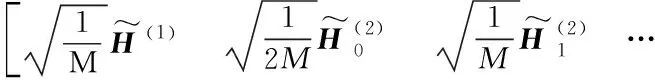
3 仿真

本節將測試非線性測量辨識算法在實際非線性系統中的辨識結果與真實系統的接近程度。從測量的角度來看，對測量結果影響最大的三個因素就是測量值的個數、測量噪聲以及測量向量的形式。因而，本文將測試這些參數對測量結果的影響。

本文選用一個常見的非線性系統，即Wiener-Hammerstein模型作為辨識對象。該模型是由一個線性環節、一個非線性環節和另一個線性環節串聯組成，如圖1所示。

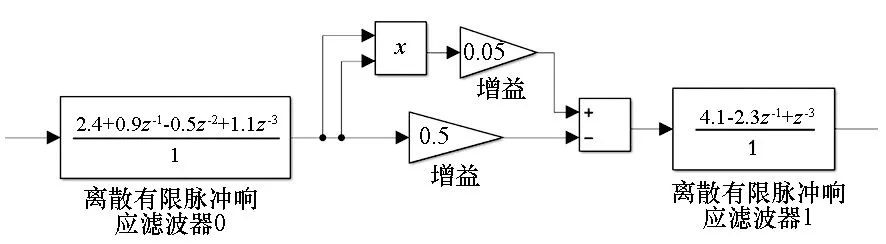
圖1 Simulink模型Fig.1 Simulink model

(11)

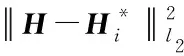
(12)

圖2呈現了兩種辨識算法在兩種測量數下的辨識結果。其中，一階核在圖2(a)中采用了折線來表示，而二階核則采用了三維柱狀圖來表示。本文定義辨識過程中采集到的系統輸出個數為測量數M，又定義測量數M與信號長度N的比率為測量比率(Measurement Ratio，MR)。圖2(a)是在MR為40%的情況下的辨識結果，圖中上半部分展現的是Volterra級數一階核的測量結果和原信號，圖2(a)下半部分展現的是二階核的測量結果以及原信號。其中，藍色代表原信號，黃色代表RLS的辨識結果，紅色代表非線性CMI的辨識結果。圖2(b)是在MR為60%的情況下的辨識結果，圖2(b)中定義同上。從這兩個圖中可以看到，本文提出的算法相比RLS算法辨識到的一階核和二階核的準確性有很大程度的提高。由于原信號是稀疏的，也就是只有靠近原點附近的項是非零的，非線性CMI方法的測量結果基本符合了這一特點，而RLS算法卻將原信號能量散布在了各項上。而且，隨著測量率的提高，可以明顯地看到非線性CMI方法的測量準確性有了進一步的提高。

(a) MR=40%

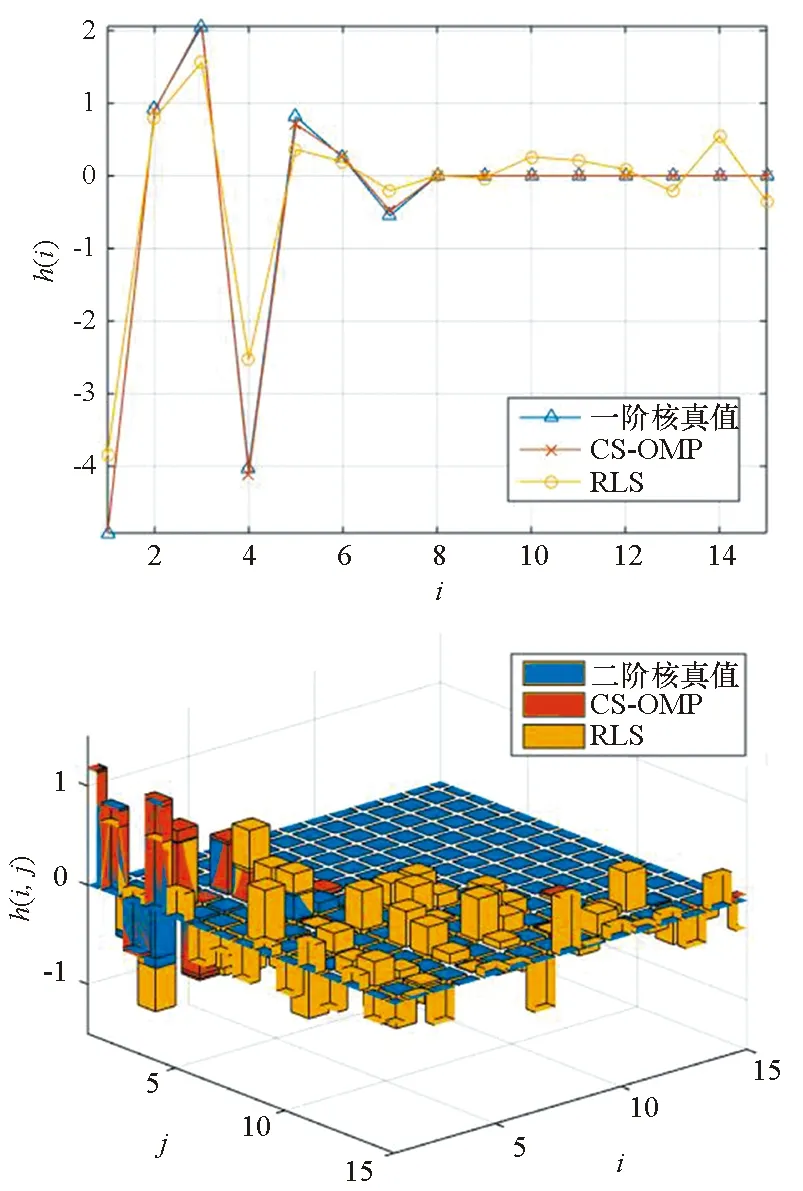
(b) MR=60%圖2 NCMI和RLS辨識得到的Volterra核Fig.2 Volterra core identified by NCMI and RLS

本文仿真了測量率從10%到200%的所有情況，并將測試結果繪制在圖3中。從圖中可以看到，當測量率達到66%時，非線性CMI的擬合程度已經達到94.13%，而遞推最小二乘算法的測量率達到177%時，其平均擬合程度才達到同樣水平。另外，當測量數大小接近于信號長度時，RLS法出現了較大的偏差。這主要是由于觀測存在誤差，而當測量矩陣接近方陣時，RLS算法的解空間越來越小，直到被壓縮到唯一解。此時，所有觀測噪聲都被納入系統模型之中，所以其偏差也就很大了。雖然，RLS算法隨著測量數的繼續增多，其結果的準確性也繼續提高，不過最終也只能達到與非線性CMI方法同樣的精度。也就是說，在該條件下，非線性CMI方法只需要90次測量就可以得到原信號，相比RLS能夠節約大概150次測量值。

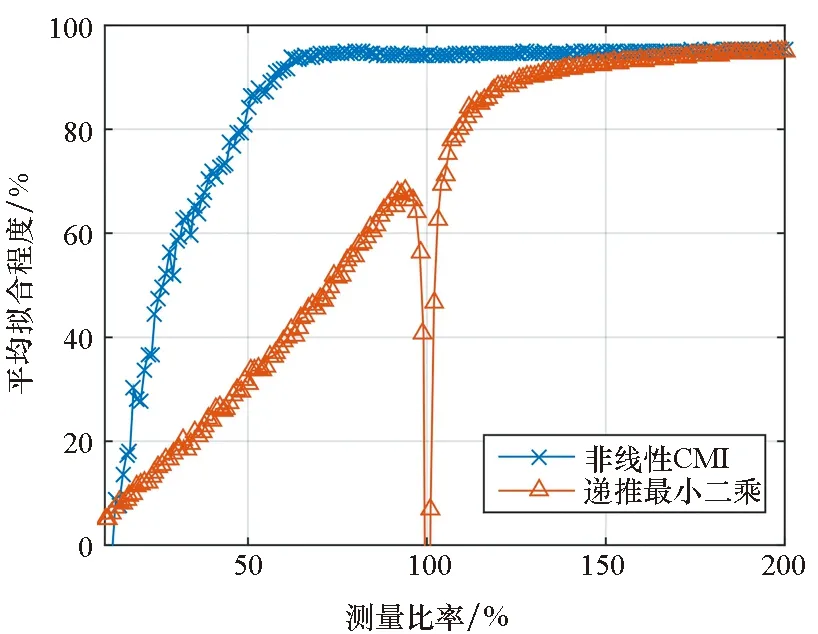
(a) 平均擬合程度與測量比率的關系(a) AFR of identification results under different MR

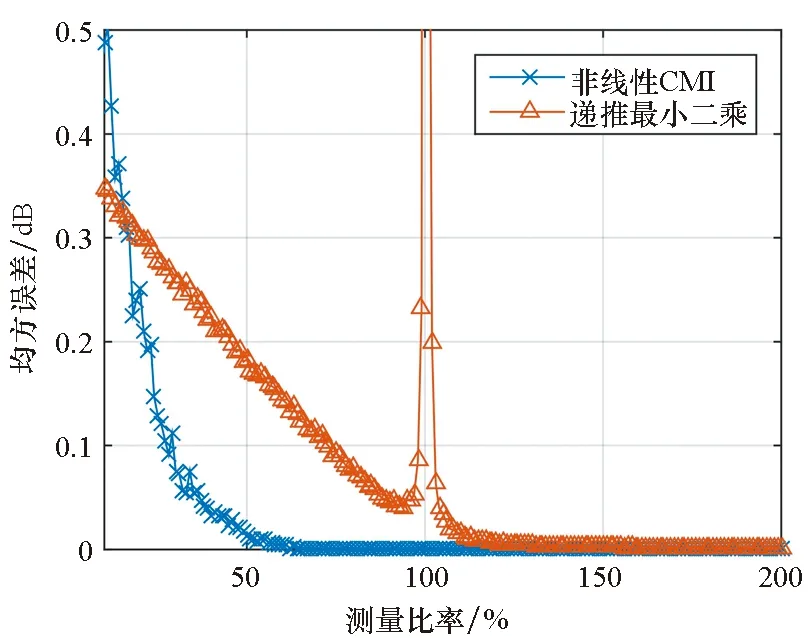
(b) 均方誤差與測量比率的關系(b) MSE of Identification results under different MR圖3 測量比率對NCMI和RLS的辨識影響Fig.3 Influence of NCMI and RLS identification results by MR

非線性CMI的測量結果在測量數達到90個時，就達到了最佳的測量結果。那么，如何確定這個數量，從而避免測量的浪費呢？在此，定義使得測量結果達到最佳的最小所需測量數為最小測量數。根據定理可知，最小測量數應該與稀疏度和信號長度有關，而稀疏度的影響遠超過信號長度。因此，本文假設Volterra核的記憶長度為30，階數為2，即信號總長度N為496。其中，非零項隨機地分布在整個信號上。圖4展示了針對不同稀疏度信號的最小測量數。根據定理可知，最小測量數應該與稀疏度的二次方成比例。但是，在線性系統中，該數值與稀疏度呈線性關系。因而，本文利用直線和拋物線分別對結果進行擬合，并且計算了兩種方法擬合結果與實際值的接近程度。其中，拋物線的平均接近程度為89.3%，而直線擬合的平均接近程度為77.9%。由此可見，最小測量數與稀疏度的二次方是同階的。換句話說，非線性CMI方法在測量過程中對信號的非零項個數更敏感。

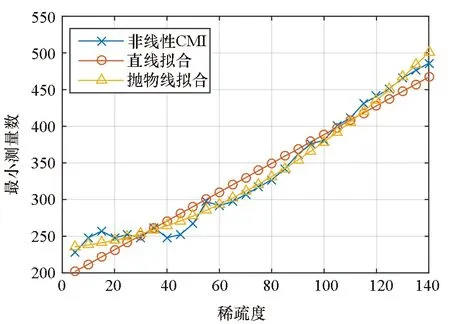
圖4 稀疏度對最小測量數的影響Fig.4 Influence of sparsity on minimum measurement number

在測量中，噪聲是不可避免的，因而在包含測量噪聲的條件下能否穩定地測量是至關重要的。對于測量算法來說，測量噪聲的絕對大小是沒有意義的，相對大小才是最重要的。因此，本文采用信噪比(Signal Noise Rate，SNR)作為指標，以測試噪聲對算法的影響。圖5展現了兩種算法在不同噪聲大小下的辨識準確度。可以看到，非線性CMI方法對噪聲具有一定的魯棒性，及時噪聲達到5 dB時，信號的平均擬合程度還能保持在69.3%的水平。

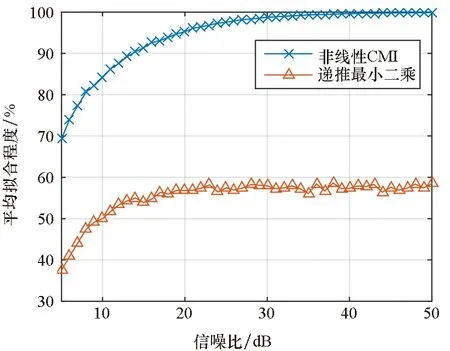
圖5 測量噪聲對辨識結果的影響Fig.5 Influence of measurement noise on identification results

除了測量數和測量噪聲以外，還有一個重要因素直接影響測量結果，那就是測量向量的形式。這是因為測量向量的形式直接決定了每次測量的方式以及測量獲得的信息多少，或者說壓縮感知正是憑借著精心設計的測量向量，從而實現高效采樣。由前文可知，選用的輸入信號是隨機地從一個高斯分布中取出的。由于一階核的測量向量是系統的輸入序列，因而一階核的測量向量是服從高斯分布的。對于二階核來說，可將核參數分為兩類，其中一類是兩個不同時刻的輸入序列相乘。由于兩個服從高斯分布的隨機變量相乘后仍然服從高斯分布，所以第一類的測量向量仍然服從高斯分布。第二類是兩個相同時刻的輸入序列相乘，因而觀測對角線信號的測量向量就不再服從高斯分布，而是服從卡方分布。圖6比較了這兩種分布對同一信號的測量結果。可以看出，雖然兩個分布的最佳測量結果是一致的，但是高斯分布比卡方分布的最小測量數要少得多。這主要是因為卡方分布的各項均是非負的，也就是服從該分布的測量空間減少了一半，那么肯定就需要更多的觀測才能達到同樣的效果。

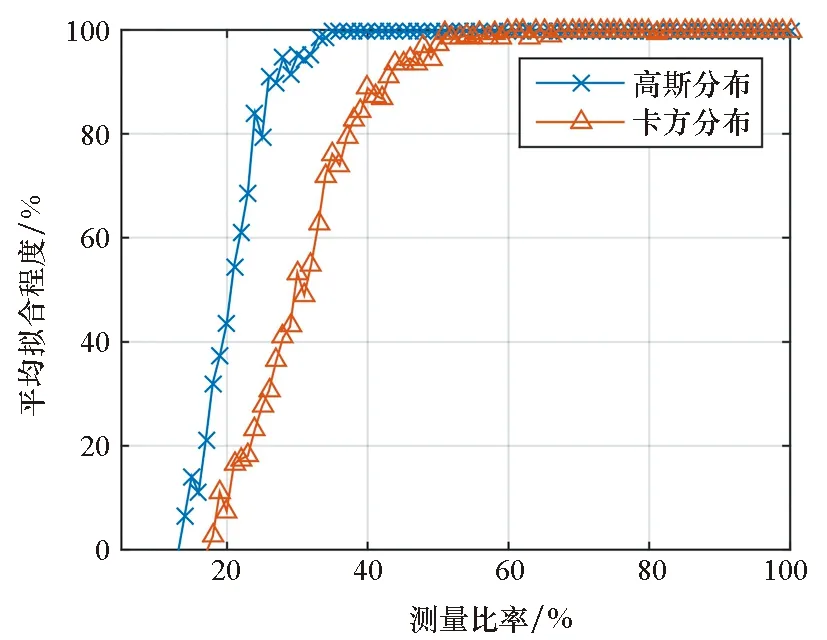
圖6 測量向量的分布對測量準確性的影響Fig.6 Influence of measurement vector distribution on accuracy

既然，Volterra二階核對角線元素的測量服從卡方分布，那么是否可以通過修改測量向量，從而提高測量效率呢？為了解決非負的問題，一個直接的方法是，將測量向量的各項減去常數，使得其均值為零。另外，如果某一列在測量中所占比例過大，那么也會影響到其他項的測量。因而，再對整個測量矩陣的每列分別做歸一化。相應地，在獲得測量結果后，要將這些修改復原才能得到原信號。圖7展示了沒有歸一化測量向量之前的測量結果，以及歸一化測量向量之后的測量結果。從圖中可以明顯地看到，在對測量向量進行歸一化后，最小測量數只需要120次測量，而此時信號的稀疏度為20。也就是說，這個最小測量數遠比定理中要求的S2lgN要小得多。由此可見，通過修改測量向量的形式從而減少觀測次數是可行的。

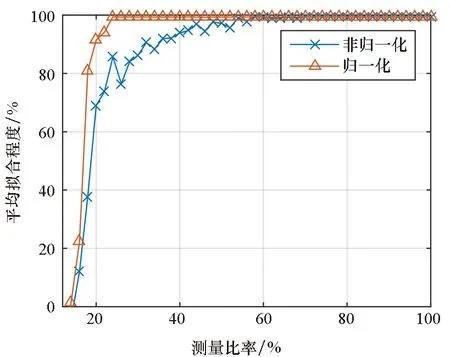
圖7 歸一化對測量準確性的影響Fig.7 Influence of normalization on accuracy

4 結論

本文的重要貢獻在于將壓縮測量算法的思想從線性領域推廣到非線性領域之中，即用測量的視角觀察非線性系統的辨識問題。首先，仿真也證明了本文提出的測量方法在沒有噪聲的情況下是可以無損地獲取系統模型，即使在有噪聲的條件下，也可以保證穩定的測量結果。其次，在測量的視角下，辨識算法更關注于信號本身的信息量或者說信號的稀疏度，而對信號長度不敏感。這就給解決“維數災難”問題指出了一條新的道路。隨后，本文在仿真中詳細分析了影響辨識結果的三個重要因素，即測量向量、測量數和測量噪聲。特別是，本文提出了一種測量向量均值歸零的方法，進一步縮減了最小測量數。這也就說明，通過設計合理的測量向量，是有可能進一步提高測量效率，使得測量數控制在稀疏度的常數倍范圍內。在同等測量次數下，利用本文提出的方法可以獲得更多的信息，即辨識模型的記憶長度和階數規模都可以更大。當然，這兩個參數越大，Volterra模型可近似的非線性系統也就越復雜。

本文還簡述了Volterra級數的物理含義。隨后，本文將Volterra級數重新排列為符合壓縮感知測量的形式，而且將原有測量矩陣重新排列為多個循環矩陣相連。這種方法不僅給RIP的證明提供了一個基礎，還簡化了辨識算法的程序設計。本文只是針對二階以內的Volterra級數模型進行了仿真，不過，根據本文的方法可以推廣到更高階核的辨識上，該方向也將是未來的研究重點。此外，本文使用的是高斯分布組成的隨機測量向量，隨后將繼續探索其他形式的測量向量，爭取進一步地縮減最小測量數，提高測量效率。另外，本文提出的方法不僅可以用于Volterra級數，還可以用于其他非線性核的線性組合表示的模型辨識問題之中。