基于子空間分解類算法的高精度頻率估計

多 濱，羅俊松，賈 勇，鐘曉玲，郭 勇

(成都理工大學信息科學與技術學院 成都 610059)

無線通信信號處理領域中實時高精度的頻率估計對全數字解調器的解碼具有十分重要的理論和實用價值。在眾多頻率估計算法中，快速傅里葉變換法是經典譜估計理論中的重要算法和理論基礎，尤其適用于確定性長信號的譜估計，具有算法復雜度低、計算量小、易于硬件實現的特點，但需要對信號實現整周期采樣，否則會導致嚴重的頻率泄露和柵欄效應，應用受到了極大的限制[1]。子空間分解類算法源于現代空間譜估計理論，一般分為兩類：一類是噪聲子空間類算法，典型代表為多重信號分類法(multiple signal classification,MUSIC)[2]；另一類是信號子空間類算法，典型代表為旋轉不變技術估計信號參數法(ESPRIT)[3]。求根MUSIC(RMUSIC)算法則是用求多項式根的方法避免了傳統MUSIC算法的譜峰搜索過程，極大地降低了計算復雜度，具有更高的頻率分辨率，但在極低的信噪比(signal to noise ratios,SNR)下，該算法估計精度略有不足[4-5]。ESPRIT算法作為信號子空間類算法也同樣具有較高的估計精度，通過兩次特征值分解就可以直接估計出接收信號的頻率，但計算量相對較大[6-10]。

目前，結合法作為提高頻率估計精度和降低硬件實現復雜度的有效方法得到了廣泛的關注。文獻[11]首先提出了一種將FFT和FFT結合的算法(本文稱為F-F算法)，提高了頻率估計精度，降低了計算量。文獻[12]將FFT和MUSIC相結合(本文稱為F-M算法)，用于間諧波的頻率估計，不僅解決了FFT算法的頻率泄露和柵欄效應問題，同時避免了耗時的譜峰搜索過程。文獻[13]將ESPRIT和RMUSIC(本文稱為E-RM算法)聯合，可用于解決數字解調器的頻率估計問題，通過計算復數矩陣向量的乘積，在一定程度上降低了計算復雜度，并保持較高的頻率估計精度。

高精度和實時性要求的矛盾一直都是頻率估計在高速全數字解調器中應用的瓶頸。因此，研究一種既保證高精度，又滿足低計算量的頻率估計算法，具有重要的應用前景。本文深入研究了基于子空間分解類算法、F-F、F-M和E-RM算法的實現特點，并針對上述技術的頻率估計精度仍有不足和計算量仍較高的問題，分別提出了將RMUSIC與FFT結合(本文稱為 R-F算法)和將ESPRIT與FFT結合(本文稱為E-F算法)的頻率估計算法，通過對信號頻率的預估計，再利用加窗插值FFT算法在已確定的細化域內完成精估計。針對這兩種算法在高低SNR下的不同性能，本文還提出了一種具有可選結構的RF-or-EF算法，通過事先設定的SNR閾值，能夠自適應地選擇R-F算法或E-F算法進行頻率估計，滿足各種SNR條件下的頻率估計需求。仿真結果表明，本文所提出的算法具有頻率估計精度高、實時性強、計算量小的特點，不會產生頻譜泄露，優于現有的頻率估計算法。

1 基于子空間分解的信號頻率估計

基于相關矩陣特征分解的信號頻率估計是現代信號頻率估計的重要內容，其中典型的代表有RMUSIC法和ESPRIT法。

1.1 基于RMUSIC算法的信號頻率估計

假設由K個復正弦波組成的信號為：

定義接收信號向量為r(n)=[r(n),r(n?1),···,r(n?M+1)]T，則有：

式中，

式中，n=1,2,···,L，L為樣本采樣點數；表示矩陣復共軛轉置。

由于aH(ωk)(k=1,2,···,K)與Ez正交，故可定義：

式中，zk=ejωk(k=1,2,···,K)是方程的根。根據求得的根即直接估計出信號頻率，其估計的頻率誤差比MUSIC算法小，精度更高[14-15]。

1.2 基于ESPRIT算法的信號頻率估計

ESPRIT算法是另一種基于子空間思想的信號頻率估計算法，即利用信號子空間的旋轉不變性求解出信號的特征參數。

假設解調器接收到的信號仍為式(2)所示向量。定義隨機過程并分別定義向量y(n)和矩陣 Φ 為：

式中，旋轉算子 Φ 滿足 ΦHΦ=ΦΦH=I，I是秩為M的單位陣。因此，由式(2)和式(6)可得：

由于s(n+1)=Φs(n)，所以式(8)可以表示為：

接收向量的自相關矩陣為：

對Rrr進行特征分解，得到Rrr的最小特征值λmin=λM=σ2(λ1≥ λ2≥···≥ λM)，由 式(10)和 式(11)，定義如下矩陣對 {Crr,Crv}：

若存在標量 λ和非零向量u，使得方程：

成立，則這樣的標量 λ稱為矩陣對 {Crr,Crv}的廣義特征值[7]。當矩陣Crr?λCrv是奇異時，該方程中的向量u有非零解，即行列式滿足：

故求解式(15)可以得到矩陣對 {Crr,Crv}的廣義特征值為

2 R-F高精度頻率估計算法

從上一節介紹可知，RMUSIC算法具有很高的頻率分辨率，且不需要搜索整個譜峰，但在低信噪比時分辨力還不夠。而FFT算法實現復雜度低、硬件易于實現，但對于信號非整周期采樣，則應用受到限制[16]。

基于上述問題，首先提出R-F高精度頻率估計算法，具體步驟如下：

1)根據L個樣本觀測值r(0),r(1),···,r(L?1)，確定接收信號表達式；

4)確定M-K個噪聲子空間的特征向量；

5)求解式(5)，得到接收信號頻率的初步估計值；

6)確定細化域。執行完步驟5)后，可以初步獲得信號頻率的粗略估計。因為真實頻率就在很小的范圍內，如果只在一個很小的區域內搜索，無疑會大大縮短搜索過程。由于RMUSIC算法精度相對較高，可以減小搜索范圍，降低了算法計算量，增強了實時性。因此，確定FFT算法的估計范圍為：

7)執行加窗FFT算法進行精估計，通過頻率細分在已經確定的狹小的區域內尋找譜峰位置。在搜索范圍S1上用FFT算法進行如下計算，確定待估頻率，其表達式為：

式中，x(n)和X(f)分別代表信號的采樣序列及其相應的變換系數；fs為采樣頻率。本文在FFT算法的基礎上，選取頻率檢測精度較高、頻譜泄漏抑制效果好且計算量較小的Hanning窗對信號進行截斷，由文獻[1]可知，信號x(n)經過加Hanning窗截斷后得到的序列為：

式中，wH(n)=0.5?0.5cos(2πn/N),n=0,1,2,···,N?1為所加Hanning窗，N為采樣點數。R-F算法實現時的程序設計流程如圖1所示。

由于Hanning窗函數的旁瓣衰減較大，通過對信號x(n)進行采樣截斷，能夠克服各頻譜之間所產生的干擾，從而大幅度減小柵欄效應和頻譜泄漏，不僅降低了頻率估計的計算量，還可較精確地估計出各種頻率信號的頻率。

可以任意設定細化域分辨率R3，但只有當R3選取恰當時，才能同時保證頻率估計的高精確性和低計算量。因此，S1范圍較大時，R3值可以取得較小，以降低計算量；S1范圍較小時，R3值可以設置得大一些，以提高估計精度，且具體的取值，需折中處理，取決于實際的需求。

R-F算法將頻率預估計和精估計分析過程有機地結合在一起，經過預估計后，確定了細化域，大幅度縮短了搜索頻率的過程，并通過加窗技術，濾除了其他頻率分量和高斯白噪聲，提高了頻率估計精度和頻域穩定性，降低了計算量。

3 E-F高精度頻率估計算法

為了進一步降低實現復雜度，并充分利用ESPRIT算法在低信噪比條件下頻率分辨率較高的特點[17]，結合計算量較小的FFT算法，本節提出了第二種高精度頻率估計算法，即E-F算法。

與R-F算法類似，E-F高精度頻率估計算法具體步驟如下：

1)根據L個樣本觀測值r(0),r(1),···,r(L?1)，確定接收信號表達式；

6)確定FFT算法的估計范圍為：

7)執行加Hanning窗FFT算法，確定最終頻率估計值。

4 EF-or-RF高精度頻率估計算法

在實際工程系統中，噪聲是無法避免的，因此必須分別考慮本文所提出的方法在不同SNR環境中的估計精度問題。基于R-F和E-F算法，提出一種EF-or-RF選擇性頻率估計算法，分別解決不同SNR下的高精度頻率估計問題。從前文可知，RMUSIC算法和ESPRIT算法分別在高SNR和低SNR條件下頻率分辨率較高。因此，該算法的基本思想是在接收到信號r(t)后，首先進行SNR判定，用SNR的先驗知識決策選擇E-F或R-F算法。頻域估計法是信噪比估計算法中的一種經典算法，通過對接收信號采樣，能夠在頻域中對信噪比進行直接估計[18]。然后，在SNR判定模塊中設置一個閾值，定義此閾值為T，如果SNR小于該閾值，則選擇R-F算法進行頻率估計，反之選擇E-F算法。具體操作為設置一個標簽F，如果SNR＞T，則F=0，表明選擇R-F算法；否則，F=1，表示選擇E-F算法。對于閾值T的選擇，如果T值較低，則導致大部分的判定都會趨向選擇E-F算法，那么在高SNR時，頻率估計性能精度不夠；而如果T值較高，則有可能在低SNR時更傾向于選擇R-F算法而沒有選擇E-F算法，故導致低SNR頻率估計精度不足。因此，該方法是將R-F算法與E-F算法有機地結合在一起，既滿足高SNR高精度頻率估計需求又能滿足低SNR高精度頻率估計需求，實現結構框圖如圖2所示。因SNR判定模塊中的頻域估計算法計算量相對較少，復雜度較低，有較高的估計精度，故圖2算法結構并不會引入額外的計算復雜度。

5 仿真結果與分析

本節主要通過MATLAB仿真軟件模擬不同SNR的無線信道環境，驗證數字解調器采用不同頻率估計算法對接收信號估計的精度。仿真參數設置如表1所示。

表1 仿真參數設置

5.1 頻率估計算法的精度比較

為了進一步確定R-F算法和E-F算法的精度，以及EF-or-RF選擇性高精度頻率估計算法的可行性，下面分別在SNR高、低兩種環境中將已有的幾種頻率估計算法與本文提出的算法進行比較，如表2和表3所示。

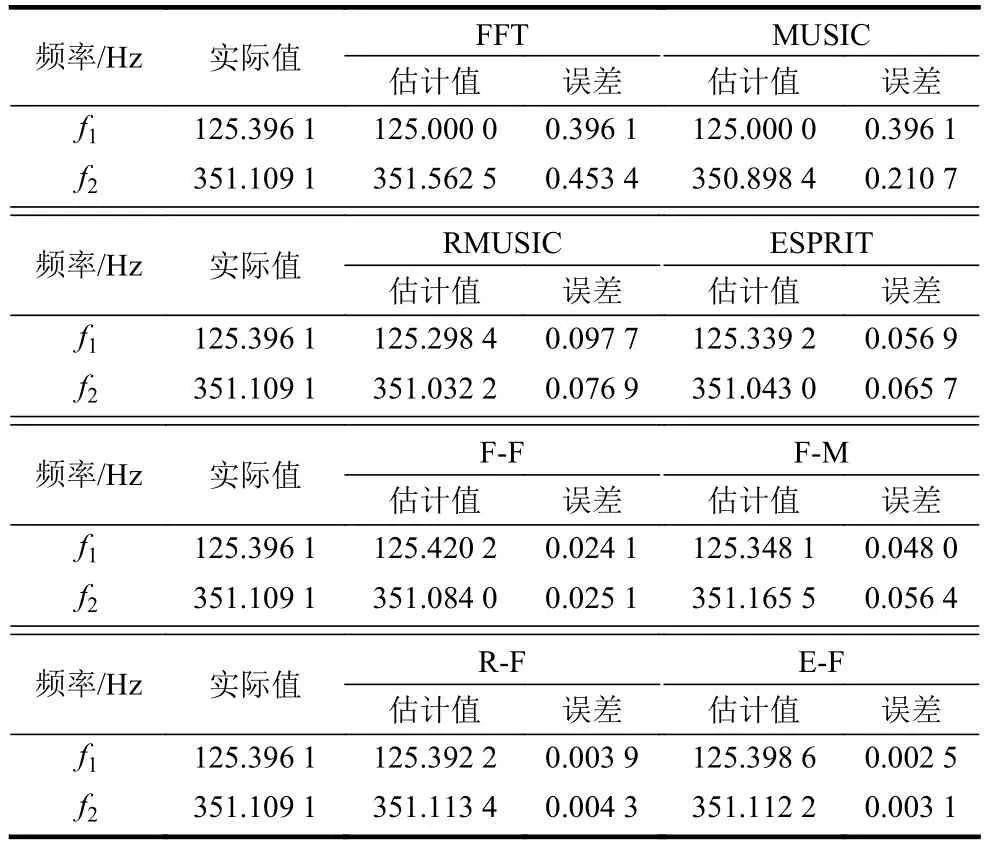
表2 SNR=-5 dB時，頻率估計值和估計誤差性能比較

表2中，由于噪聲功率非常大，傳統的FFT算法和MUSIC算法都無法準確地估計出f1和f2，頻率估計的精度不高，但ESPRIT算法的頻率估計誤差相對較低，這證實了相對于其他傳統的頻率估計算法，ESPRIT算法在低SNR下仍具有較好的頻率估計精度[18]。此外，相比于F-F和F-M算法，本文提出的R-F算法和E-F算法的估計精度更高，對于低SNR時的噪聲都有良好的抑制效果，對頻率的估計精度可達到小數點后2位，且E-F算法的估計誤差低于R-F算法。

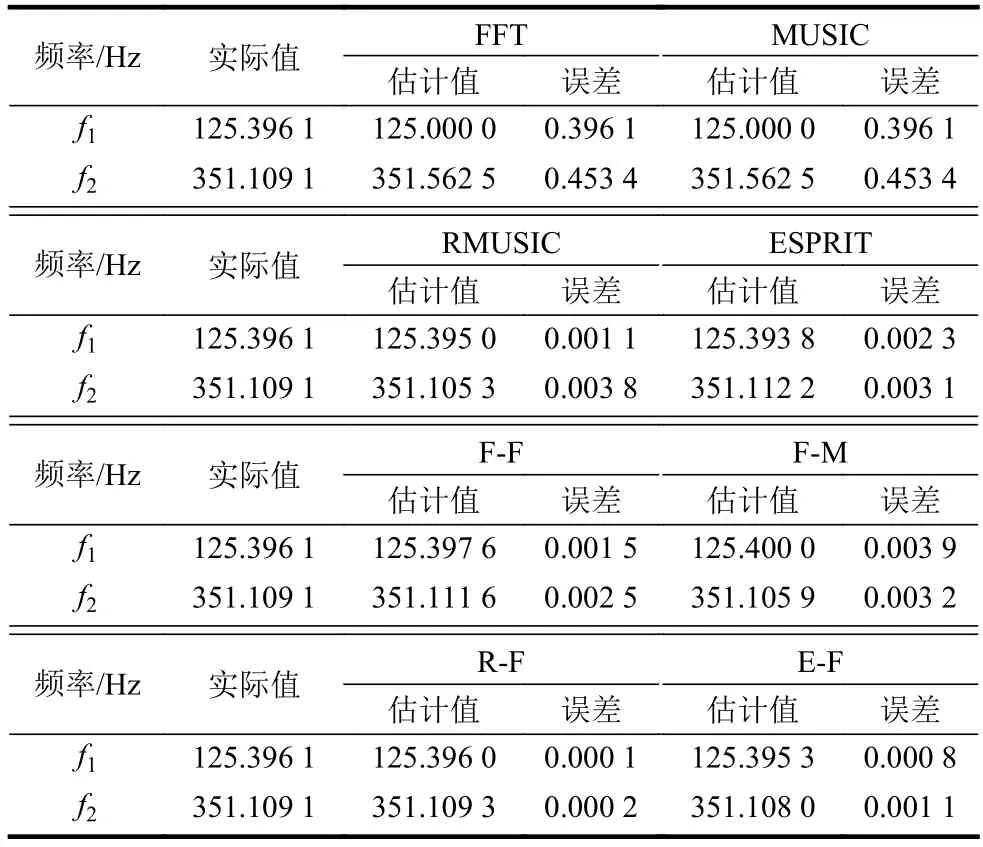
表3 SNR=25 dB時，頻率估計值和估計誤差性能比較

從表3中可以看出，由于計算點數不夠，FFT算法和MUSIC算法并不會隨著SNR的增加而提高估計精度。在高SNR條件下，RMUSIC算法和ESPRIT算法的估計誤差非常接近，且R-F與E-F兩種算法對頻率估計都非常理想，高于F-F算法和F-M算法的估計精度，但R-F算法的估計精度更高，幾乎可以達到小數點后4位的精度。

基于以上仿真結果可知，盡管R-F和E-F兩種算法都作了相似程度的細化域估計，但由于RMUSIC算法和ESPRIT算法的不同，導致它們對噪聲的敏感程度也不盡相同。在高SNR時，R-F算法的優勢非常明顯，故可以直接應用R-F算法就可基本達到小數點后4位的精度。但在低SNR的惡劣環境中，E-F算法的頻率估計性能優于R-F算法，具有較強的抗造能力。

5.2 性能分析

本節主要比較本文提出的R-F和E-F算法與F-M算法[12]和E-RM算法[13]在不同SNR條件下估計頻率f1的根均方誤差(root mean square error,RMSE)、計算復雜度和仿真處理時間。RMSE常被用來描述頻率估計算法的性能，計算方法如下[19]：

式中，N是獨立進行蒙特卡洛仿真的次數；是對f1第i次仿真頻率的估計值；f1是頻率的真實值。具體仿真參數仍如表1所示。

圖3描述了隨著SNR的變化，以上4種算法的RMSE性能。仿真結果表明，RMSE性能隨著SNR的增加而不斷降低，說明這幾種算法都對噪聲比較敏感，頻率估計精度也都會隨著SNR的增加而得到改善。從圖3還可以看出，本文提出的R-F和E-F算法的RMSE性能都明顯優于F-M算法，并且E-F算法在低SNR下略優于R-F算法，而R-F算法在高SNR下占據明顯的優勢。此外，通過與E-RM算法比較可以看出，在中低SNR下，E-RM提供了與R-F和E-F算法相近的性能，但在高SNR下，R-F算法的性能更好，原因是在細化域利用加窗FFT算法進行二次頻率搜索，可以獲得更加準確的頻率估計值。

在實際應用當中，頻率估計算法的精度是影響性能的重要因素，但算法的計算復雜度也同樣重要。一般來說，FFT算法的復雜度為O(LlogB)，其中B為可重疊窗函數的個數[20-21]。MUSIC算法和ESPRIT算法的復雜度分別為O(M2P+M2L)和O(M3+M2L)[22]。MUSIC算法需要頻譜搜索，且當估計頻率數P＞M時，比ESPRIT算法復雜度更高，而RMUSIC算法僅需要通過子空間分解來估計頻率，不需要頻譜搜索，其復雜度僅為O(M2L)。所以，F-M、R-F、E-F和E-RM這4種算法的復雜度分別為O(LlogB)+O(M2P+M2L)、O(LlogB)+O(M3+M2L)、O(LlogB)+O(M2L)和O(M3+M2L)+O(M2L)。從4種算法的復雜度比較可以看出，E-RM算法的復雜度最高，RF算法的復雜度最低。E-F算法更適用于M值較小和所需估計頻率數較大的情況。

表4給出了F-M算法、R-F算法、E-F算法和E-RM算法在不同的M值和SNR=10 dB時，估計頻率f1所需處理時間的比較。從表4可以看出，雖然增加M值也會在一定程度上提高頻率的估計精度，但各算法也會因為矩陣維度的增大而明顯增加計算量。在相同的M值和較小的P值條件下，本文提出的R-F的仿真耗時均小于F-M和E-RM算法，尤其是在M值較大時，差異更加明顯。盡管在中低SNR下E-RM算法的性能略優于E-F和R-F算法，但是本文提出的算法消耗更少的時間，計算更加有效，滿足實時性要求。

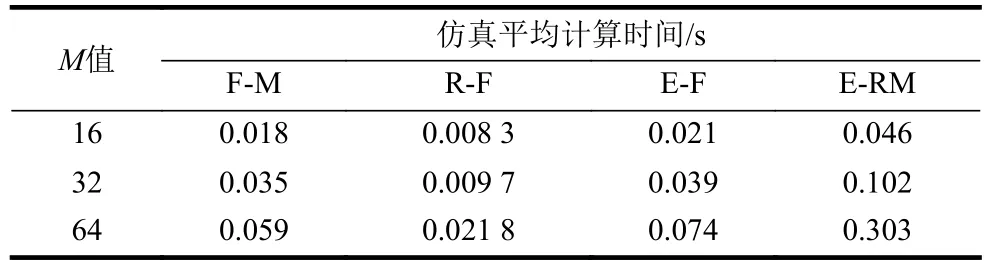
表4 不同算法耗時比較

本文提出的R-F和E-F算法能夠更快速更準確地估計出兩個甚至多個信號的頻率，實現高精度頻率估計。在此基礎上，通過R-F和E-F算法選擇性結合的設置，既能滿足高SNR高精度頻率估計的需求，又能滿足低SNR高精度頻率估計需求，適用于各種SNR條件下的全數字接收機高精度頻率估計。

6 結 束 語

本文結合子空間分解類算法的特點，提出了R-F算法、E-F算法和RF-or-EF算法，解決了高速全數字解調器對頻率估計算法的高精度和實時性需求。首先由RMUSIC算法或ESPRIT算法對頻率進行預估計，再根據預估計值確定細化域，最后基于加窗FFT算法的思想進行精估計。通過縮小的細化域，減少了頻率估計的計算量，算法流程精簡，易于硬件實現。此外，通過R-F和E-F算法的選擇性結構，可以滿足不同信噪比條件下的高精度頻率估計需求。仿真結果表明，本文提出的算法能夠精確地估計出接收信號的頻率，與已有的頻率估計算法相比，具有更高的頻率估計精度，更低的計算時間，在低信噪比下也能相對準確的估計出信號頻率，抗噪性能強。