Mathematica軟件在高等數學教學中的應用研究
劉熙娟,劉 云
(塔里木大學 信息工程學院,新疆 阿拉爾 843300)
一、引言
高等數學是各類高等院校多種專業(包括許多文科專業)開設的一門重要基礎理論課,對學生后續課程的學習以及思維素質的培養起著非常重要的作用。高等數學課程教學的目的在于讓學生掌握數學的基本理論、方法和技能,同時還要培養學生自覺運用高等數學的理論知識解決實際應用問題的數學能力。然而高等數學中大量復雜的計算往往使學生望而生畏,部分學生對數學的抽象性感到困惑,對枯燥的理論推導感到厭煩,從而對高等數學的學習失去信心。傳統的數學教育過分強調形式化的邏輯推導,缺乏體現數學與其他學科的橫向聯系,使得充滿活力、充滿生機、充滿美感的數學成了內容多負擔重的習題、結論和公式的堆積,也難以將數學知識運用到實際生活中去。在高等數學教學中若能采用一些數學軟件解決機械的數值計算與符號演算,把更多的精力用于加強“本質”性問題的學習,讓學生親身體會數學知識在生產、經營和管理活動中的應用,使得高等數學課程從“學數學”向“用數學”轉變,從“理論教學”到“應用教學”轉變,充分領略數學的“工具性”與“應用性”,同時革新教學手段和教學方法,定能充分調動學生的學習興趣,加深對理論知識的理解,培養應用數學的能力,以期達到教學效果的最優化。
Mathematica的出現為高等數學的學習提供了輕松的氛圍,它是集文本編輯、數學計算、邏輯分析、圖形、動畫于一體的高度優化的專家系統,是目前比較流行的數學軟件之一。Mathematica軟件的原始系統是由美國物理學家Stephen Wolfram領導的一個小組于1987年研究開發的。由于Mathematica軟件界面直觀,便于安裝,且提供了很好的幫助功能,新手容易上手,因此比較適用于高等數學的實驗教學。基于此,本文主要從具體實例出發,以高等數學為切入口,利用Mathematica軟件解決高等數學中遇到的一些具體問題。
二、Mathematica軟件的舉例說明
下面就如何借助Mathematica軟件的可視化交互功能,在高等數學符號演算、數值計算和繪圖功能等幾個方面的應用進行簡要闡述。
1.符號演算。高等數學中常見的符號演算問題,如求極限、求導數、求積分等,用Mathematica軟件來解決更能體現其優越性。
這是未定式極限問題,需用兩次洛必達法則才能求出結果,而且在計算中容易出錯。若用Mathematica軟件,只需輸入命令:Limit [(Sin [1/x]+Cos[1/x])^x,x->+Infinity)],即可得結果:e。
不定積分是積分學的基礎,要準確地計算一個復雜函數的不定積分,需要相當復雜的步驟,但是如果借助Mathematica軟件,往往可以達到事半功倍的效果。這是一個三角函數有理式的積分,需要先借助三角形萬能公式把sinx和cosx轉化成同一個三角函數,再做變量代換,最后化簡求積分,過程枯燥、煩瑣,但是在Mathematica軟件中,只需輸入命令:Integrate[(1+Sin[x])/(Sin[x]+Sin[x]×Cos[x]),x];Simplify[%],即可得結果:
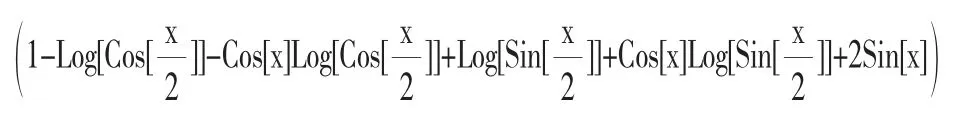
2.數值計算。Mathematica能求微分方程(組)的準確解,能求解的類型基本覆蓋了人工可求解的范圍,功能很強,但不如人靈活,輸出的結果與教材上的答案可能在形式上有所不同。此外,Mathematica求數值解也很方便,而且有利于作出解的圖形。
在Mathematica軟件中,命令如下:

可得結果:

用Mathematica軟件還可得到該微分方程在平面中表示的圖形,如圖1。
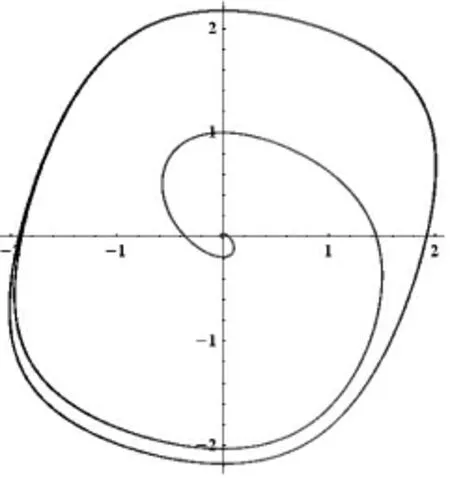
圖1

說明:上例是求一個著名方程組的數值解的問題,通過求數值解容易得到它的相圖,In[4]繪制了解的相軌線如圖1所示,由圖可知原點是奇點,極限環的形狀也可以觀察到。
3.圖形處理。在高等數學的教學中發現,空間圖形的繪制是個難題,學生對這一問題的困惑主要在于無法畫出其圖形,但是借助數學軟件這個問題就變得很有吸引力了。
例4.畫出雙曲線x2+y2-z2=1的圖形及其在3個坐標面上的投影。
在重積分的運算中,經常用到空間立體的投影區域,這需要很強的空間想象力。這類題目,如果不借助數學軟件,則無法獲得其草圖,如果借助數學軟件,這個投影區域則一目了然。當然還可以通過設置參數,使圖形更加的美觀。在Mathematica軟件中,該題命令及結果如下:


圖2
三、結論
將通用數學軟件Mathematica融入高等數學教學過程中,可以克服傳統教學中講解內容抽象、手工繪圖不準確、教學內容難以擴展等方面的不足。尤其是對于一些基礎薄弱的學生來說,這一軟件的應用可以幫助他們擺脫“聽天書”的困境和折磨,使得抽象的數學變得生動有趣,有利于提高學生學習數學的熱情與積極性。數學軟件與理論課程的整合不僅為視頻教學提供了豐富的表現手段,更為優質資源的創建提供了支撐和保障。利用數學軟件輔助教學是數學教學發展的需要,也是培養創新型實用型人才的需要,這對于提高教學質量、推動教學改革具有極其重要的理論意義與實際意義。

