多充液貯腔航天器耦合動力學與姿態控制

劉 峰，岳寶增，唐 勇

(北京理工大學宇航學院，北京 100081)

0 引 言

隨著現代航天器內的液體推進劑的質量占比不斷提高，液體晃動動力學問題和有關的控制研究已經成為航天器總體設計中的核心問題之一[1-2]。在軌充液航天器內的液體晃動特別是大幅液體晃動具有比較低的固有頻率，很有可能與航天器上的大型柔性附件及控制系統發生動力學耦合共振，這可能導致航天器結構的破壞或者姿控系統失效而使航天器姿態翻滾[3-4]。因此，現代航天工程中迫切需要建立準確、高效且適用性強的液體大幅晃動類航天器耦合系統動力學模型。

考慮到推進劑包含燃燒劑和助燃劑兩種以上不同液體，航天器上往往需要攜帶多個卡西尼腔(或者球腔)。與單腔不同，各個貯腔尺寸及安裝位置差異、推進劑消耗不均、不同液體特性等諸多因素，使得多個貯腔內的液體晃動與航天器主體之間的動力學耦合特性更為復雜。而關于這方面現有的研究極少，更多的研究工作有待進一步的完善。本文所建立的四充液貯腔航天器耦合動力學模型具備較強的適用性，模型中不僅考慮了航天器主體軌道平動與姿態轉動，而且還包含有諸如貯腔的幾何尺寸、布放位置、充液比及液體物理特性等反映耦合系統動力學特征的重要的工程參數。

Berry和Tegart[5]首次提出了等效液體晃動質心面模型，并基于此模型編制了相應的大幅晃動(Large amplitude slosh, LAMPS)Fortran程序，通過大量二維情形的低重力晃動試驗驗證了LAMPS程序在預測液體晃動力上的準確性。另一方面，文獻[6-7]將二維質心面模型發展到三維情形，考慮單個貯腔作水平橫向簡諧運動時，通過對比由Fluent軟件模擬得到的液體晃動力驗證了質心面模型用于航天器貯腔大幅液體晃動分析的有效性；隨后，采用牛頓-歐拉法將質心面模型整合到充液航天器耦合姿態動力學模型中，編制相應的Fortran程序對單貯腔航天器姿態機動問題進行了仿真計算，并與歐洲航天局2005年發射的液體晃動實驗衛星(單貯腔衛星)的在軌測量結果進行了對比，驗證了質心面模型應用于大幅晃動類充液航天器耦合動力學建模的可靠性。此外，文獻[8] 進一步改進和發展了質心面模型。盡管如此，等效液體晃動質心面模型在等效液體黏性耗散力以及液體運動約束等方面尚有很大的研究空間[5]。

本文結合中國某型號航天器預研要求，基于已有的質心面等效模型，采用拉格朗日方法，系統地建立了任意復雜激勵下四貯腔航天器剛-液耦合動力學精確模型，盡管在準確度上可能不及CFD-剛體耦合動力學模型[9]，但是由于該模型所需求解的自由度遠遠低于CFD-剛體耦合動力學模型，能夠實現與航天器控制系統進行快速高效的實時數據交互。然后，編制了相應的MATLAB仿真計算程序，考慮失重環境下航天器受復雜激勵情形，通過對比Flow3D求解所得的液體推進劑產生的晃動力及晃動力矩結果，驗證了所建模型的可靠性；同時，得到了特定工況下質心面模型的等效摩擦特性系數隨貯腔充液比的經驗關系。最后，考慮此類航天器在進行三軸穩定姿態機動時，液體晃動將可能對航天器的姿態運動帶來強烈的擾動。為此，基于本文建立的耦合動力學模型，初步設計了相應的姿態機動補償控制器，結果顯示該補償控制器能很好地抑制航天器姿態角速度的振蕩。

1 四充液儲箱航天器剛-液耦合動力學建模

1.1 質心面模型與儲箱布局介紹

1975年，Berry和Tegart[5]提出了一種適用于求解微重力環境下液體晃動力的大范圍運動及大幅晃動模型，該模型將貯腔內的所有液體等效為點質量并沿特定的約束表面運動，因此也稱為質心面模型。如圖1所示，針對航天器工程中主要采用的兩類液體貯腔：卡西尼腔和球腔，質心約束表面(質心面)為一旋轉橢球面，在腔體坐標系下質心面的曲面方程有如下表示：

(1)

特別地，對于球腔，有a=b。

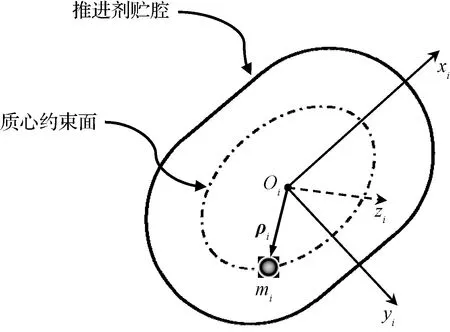
圖1 質心面模型示意圖Fig.1 Illustration of the constraint surface model forliquid sloshing

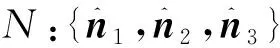
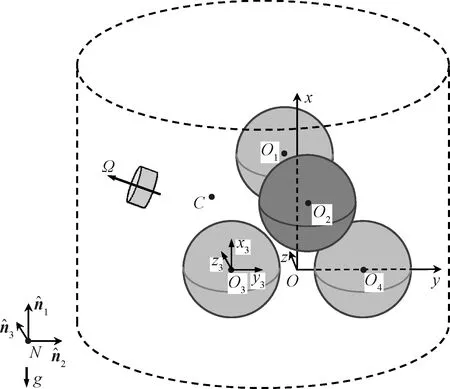
圖2 航天器四貯腔布局與坐標系Fig.2 Four tanks layout in spacecraft and frames

1.2 系統運動描述

1)航天器相對于慣性參考系的轉動

采用航天器整體坐標系相對于慣性參考系發生的轉動來描述航天器的姿態運動，并使用無奇異的歐拉四元數描述法來定義航天器姿態矩陣

(2)

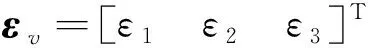
設航天器的轉動角速度矢量在整體系中的坐標矩陣為

并由此規定任意矢量在整體系中的坐標表示方法。

由四元數表示的航天器姿態運動學方程則由如下關系式定義：

(3)

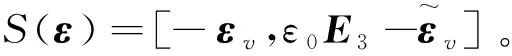
此外，重力加速度矢量在整體系下的坐標表示為：

(4)

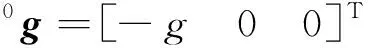
2)航天器相對于慣性參考系的平動

航天器主剛體質心在慣性參考系下的位置和速度所對應的坐標矩陣分別記為

(5)

(6)

于是主剛體質心的絕對速度矢量在整體系下的坐標表示為

(7)

3)液體等效質心點的運動

記第i個液體質心點相對于慣性系的位置矢量在整體系下的坐標表示為

1ri=1rOi/N+1ρi

(8)

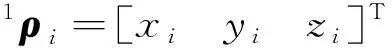
式(8)對時間求絕對導數，可得質心點的絕對速度在整體系中的坐標表示：

記Ri=1rO/C+1rOi/O+1ρi，質心點的絕對速度在整體系中的坐標矩陣最后可表示為

(9)

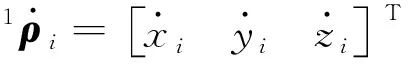
1.3 剛-液耦合系統動力學方程

本文采用混合坐標意義下的Lagrange方程[10-11]建立四充液貯腔航天器耦合動力學模型。建模過程需要計算航天器主剛體、儲腔內液體及動量輪組成的耦合系統的動能和勢能。設航天器主剛體的質量為mhub，關于其質心坐標系的慣性張量為Ihub；動量輪的慣性張量為Iw。

系統的動能由如下定義式給出

(10)

式中：mi是第i個質心點的質量，數值上等于對應貯腔內液體總質量；Ω是動量輪相對整體系的轉動速度。

將式(9)代入式(10)并整理成矩陣形式：

(11)

只考慮系統的重力勢能

(12)

將式(4)、(5)、(8)代入式(12)得到系統勢能的矩陣形式：

(13)

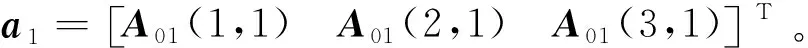
于是，該耦合系統的Lagrange函數有如下表述：

(14)

1)航天器主剛體平動的動力學方程

以航天器主剛體質心的位置坐標和速度坐標表示的Lagrange方程為

(15)

式中：F是航天器系統受到的外力的合力在慣性參考系中表示的坐標矢量，其作用點位于主剛體質心。當不計入航天器主剛體及貯腔的質量時，由牛頓第二定律，F即表示四個貯腔內液體對航天器主剛體總的等效作用反力。

把式(11)、(13)同時代入式(14)后再代入式(15)，最終得到描述航天器沿軌道平動的動力學方程：

(16)

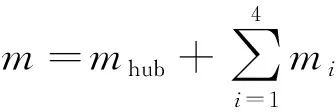
2)航天器主剛體轉動的動力學方程

偽速度(ω)下的廣義Lagrange方程為

(17)

式中：M是航天器系統受到關于主剛體質心的外部作用力矩的合力矩在整體系中表示的坐標矢量。當不計入航天器主剛體及貯腔的慣量并不考慮動量輪作用時，由力矩平衡關系，M即表示四個貯腔內液體對航天器主剛體總的等效作用反力矩。

最終得到描述航天器姿態轉動的動力學方程：

(1ω)×[Imb(1ω)+Iw(1ω+1Ω)+

(18)

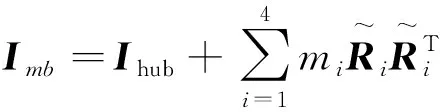
3)質心點運動的動力學方程

以第i個質心點的位置坐標和速度坐標表示的Lagrange方程為

(19)

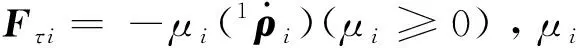
最終得到的描述質心點運動的控制方程為：

(20)

此外，動量輪的輸出方程有如下表述：

(21)

1.4 求解質心面約束力

對于第i個貯腔，質心面在腔體坐標系下的曲面方程如式(1)表示，當質心點被約束在質心面上運動(聯系運動)時，其沿曲面外法向ni的速度投影應始終為0，即有

(22)

并且有

(23)

式(22)對時間求微分可得聯系運動的約束條件為

(24)

將式(23)代入式(24)，得

(25)

再將式(20)代入式(25)，可得質心點受到的法向支持力大小為

(26)

2 復雜激勵下等效晃動力與等效晃動力矩驗證

為了驗證基于等效液體晃動質心面模型，根據我國某型號航天器預研的需要建立四充液貯腔航天器耦合動力學模型，這里，在航天器主剛體質心處施加全自由度的加速度激勵，將液體所產生的作用于主剛體質心的晃動力及晃動力矩的模型計算結果與Flow3D計算結果進行對比。其中Flow3D計算方案主要包括：推進劑處理為不可壓縮、黏性流體；使用單相流模型，氣體部分僅提供環境壓力，其密度相對液體很小，不進行動量計算；考慮表面張力；液固界面采用Navier滑移邊界條件；先計算得到表面張力作用下穩態時的液面構型，再以此為初始條件導入給定激勵進行計算。

給定主剛體質心同時受到1000 s的三維平動加速度激勵與三維角加速度激勵，它們的時程圖分別如圖3和圖4所示。

圖3 三維平動加速度激勵時程Fig.3 Acceleration excitation in three directions

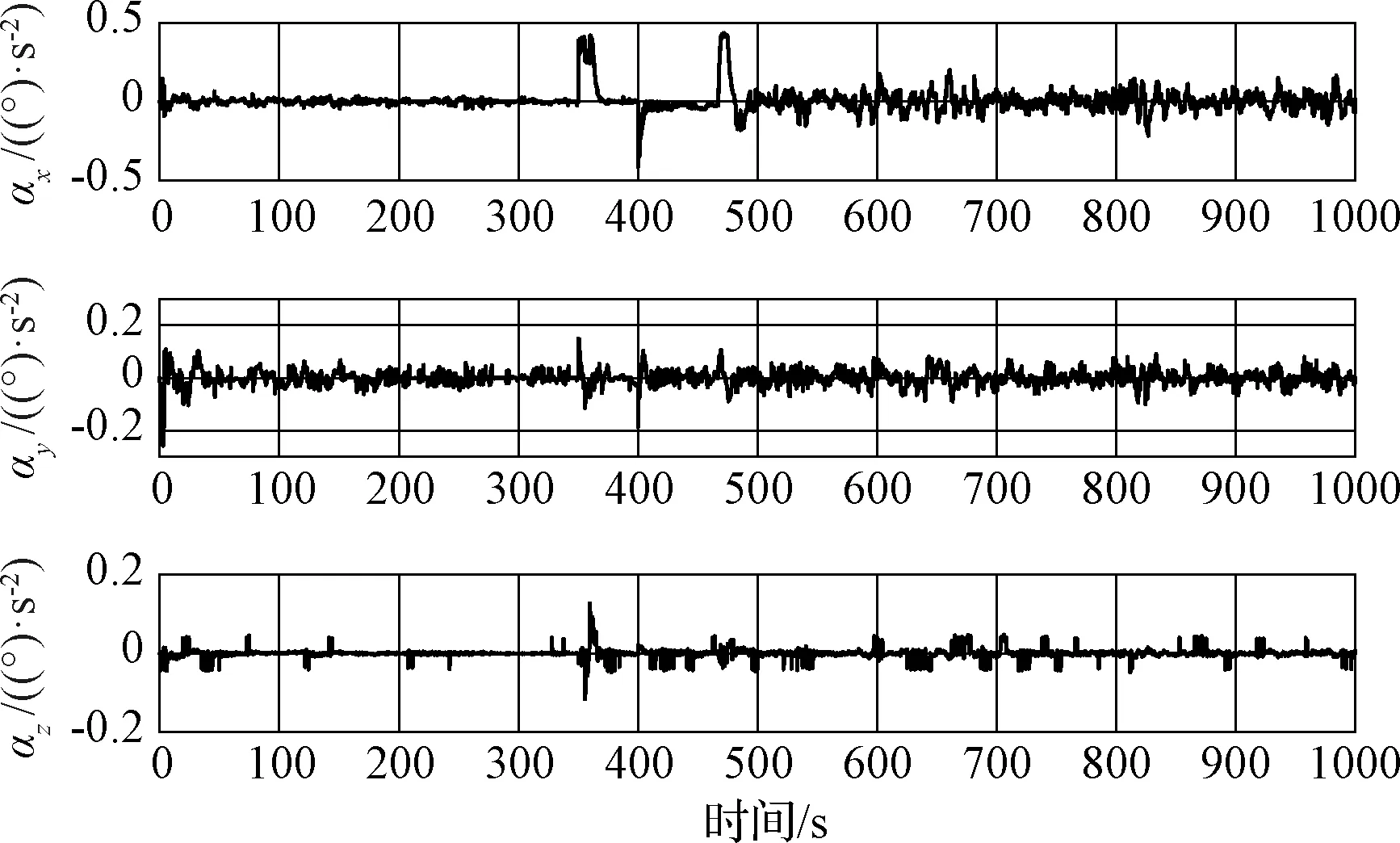
圖4 三維角加速度激勵時程Fig.4 Angular acceleration excitation in three directions

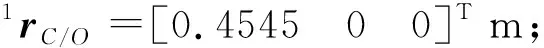
表1 推進劑特性參數Table 1 Characteristic parameters of propellant

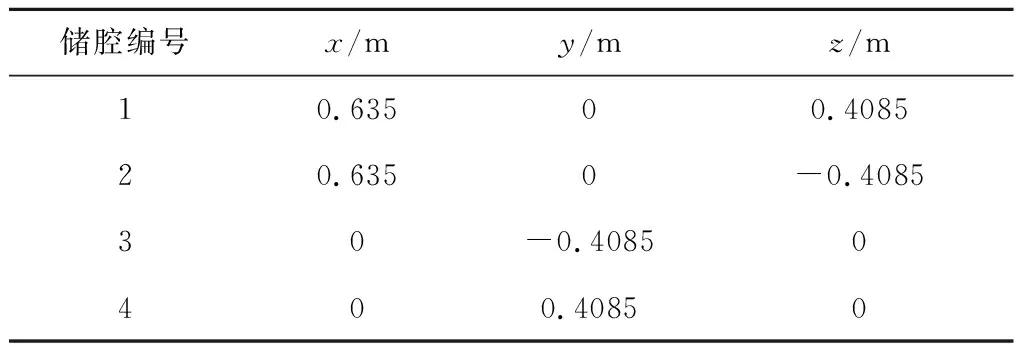
表2 充液儲腔球心位置坐標Table 2 Coordinates of the center of the tanks

本文給出了以下兩種工況下的晃動力和晃動力矩的對比結果：工況1為各推進劑貯腔充液比均為20%(圖5、圖6)；工況2為各推進劑貯腔充液比均為60%(圖7、圖8)。計算結果表明，充液比較高時，模型的計算結果更為準確，主要原因是由于當貯腔內液體越少時，同等水平激勵下晃動的幅度越大，并且Flow3D計算顯示液體出現更為明顯的破碎。總的來說，晃動力和晃動力矩的對比結果體現出較高的吻合度，說明本文建立的四充液貯腔剛-液耦合動力學模型具有應用于航天工程實際的重大價值。

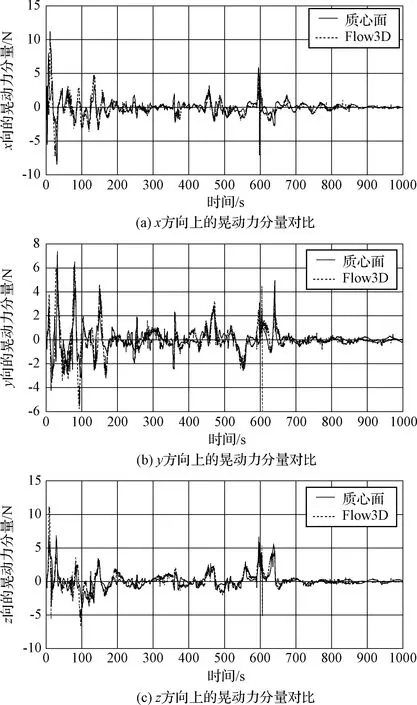
圖5 晃動力:質心面模型vs.Flow3D(工況1)Fig.5 Slosh force: model results vs. Flow3Dresults(Case 1)

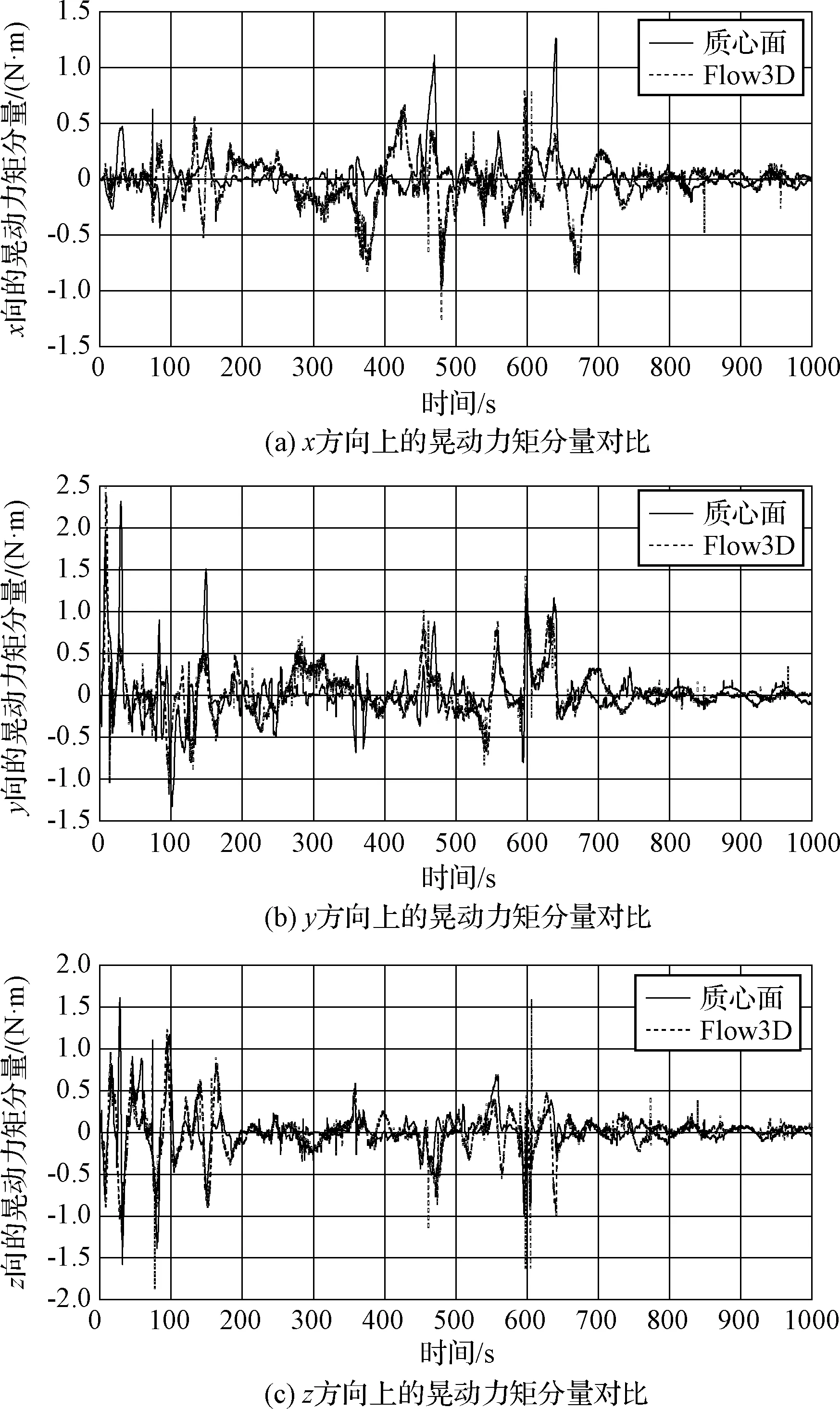
圖6 晃動力矩:質心面模型vs.Flow3D(工況1)Fig.6 Slosh torque: model results vs. Flow3D results(Case 1)

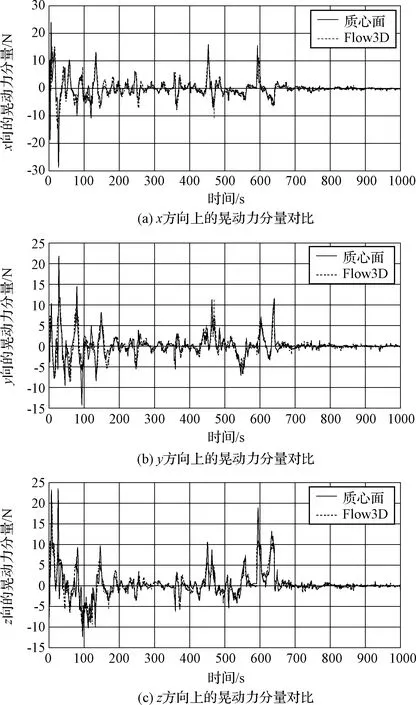
圖7 晃動力:質心面模型vs.Flow3D(工況2)Fig.7 Slosh force: model results vs. Flow3Dresults(Case 2)

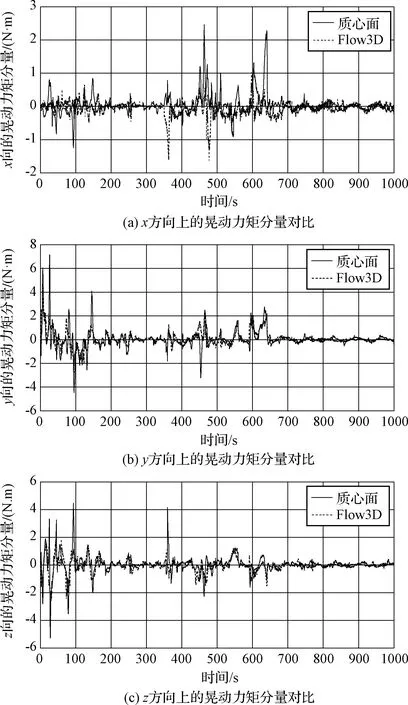
圖8 晃動力矩:質心面模型vs.Flow3D(工況2)Fig.8 Slosh torque: model results vs. Flow3D results(Case 2)

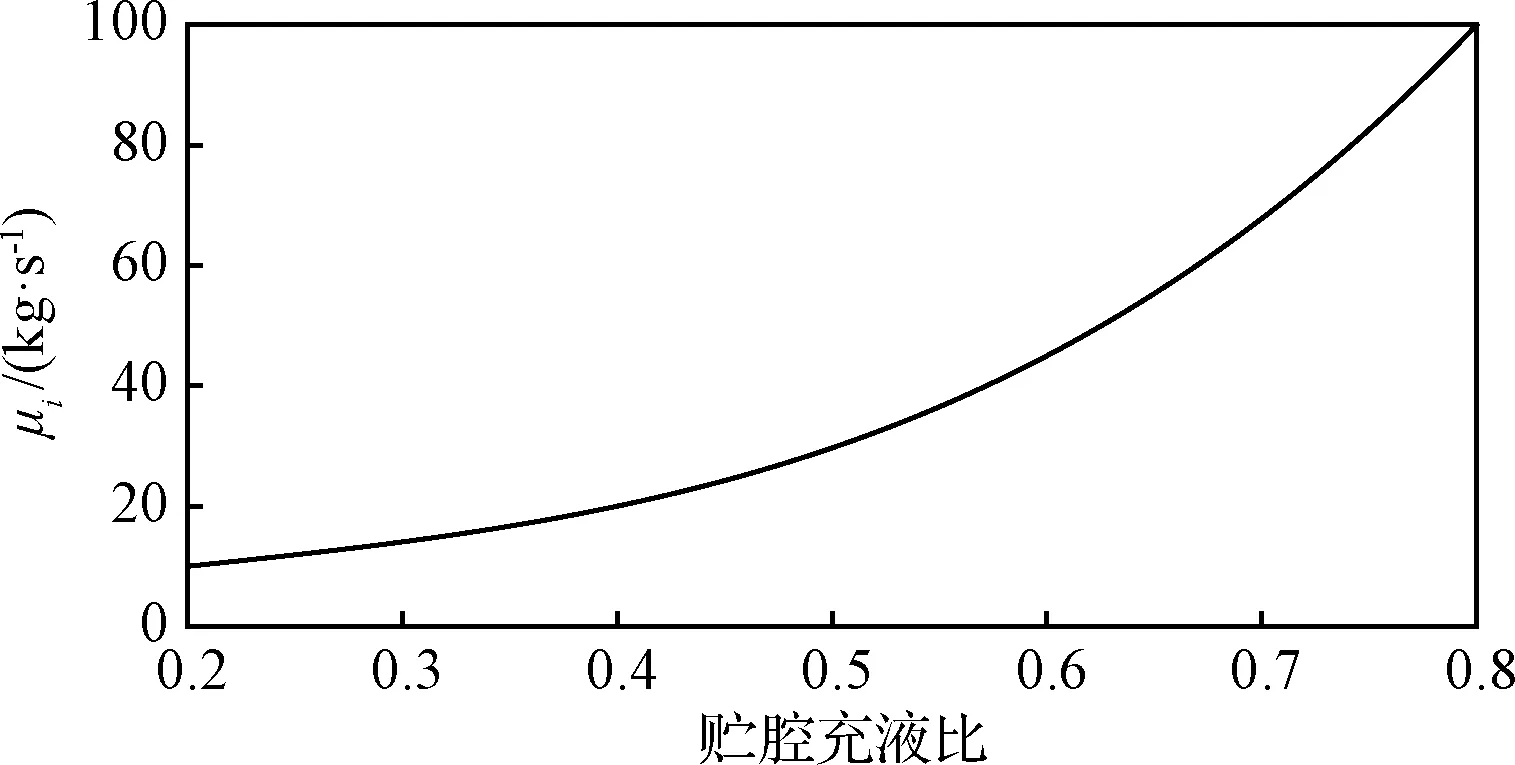
圖9 等效摩擦特性系數與充液比經驗關系Fig.9 Empirical relationship between μi andliquid-filled ratio

通過更多充液比工況下的對比研究，對于這里所給的球腔尺寸、液體黏性特性以及加速度環境，本文得到了質心面模型中的等效摩擦特性系數μi與充液比的近似經驗關系如圖9所示。

此外，本文基于質心面等效模型建立的多貯腔航天器剛-液耦合動力學模型在評估液體晃動力和晃動力矩時的計算效率遠高于Flow3D計算流體動力學仿真軟件。使用3.4 GHz的PC機，計算時長為1000 s，編制MATLAB四階-五階Runge-Kutta(ode 45)算法解算本文所建立的動力學模型只需2 h左右，而使用Flow3D仿真軟件則需3天甚至更多時間(主要取決于計算網格尺寸相關)。

3 三軸穩定姿態機動設計

本節中，不考慮航天器軌道運動，啟動動量輪對航天器進行文獻[4]中的“rest-to-rest”形式(初始角速度與末態角速度均為零)的姿態機動，并研究機動過程中的剛-液耦合動力學特性。假定各個貯腔的充液比均為60%；航天器主剛體不受到任何外部作用力矩，即M=0。

研究發現，當航天器處于完全失重環境，且不受到任何強干擾(或激勵)作用時，對航天器進行三軸穩定姿態機動過程中，主體姿態運動與液體晃動之間的動力學耦合效應不顯著。進一步考慮在軌航天器的如下工況，即航天器主發動機點火(認為是一種強干擾)產生一個持續的推力使得航天器獲得一個恒定的加速度，即航天器將處于一個等效的重力加速度環境，假定g=1 m/s2。航天器主剛體關于其質心坐標系的慣性張量為Ihub=diag(2700,1300,2300) kg·m2。

圖10為采用文獻[4]中的線性PD控制器：

Tw=kpεv+kd(1ω)

取kp=250,kd=2000，進行三軸穩定姿態機動時的航天器主體角速度響應。結果顯示姿態機動過程中，貯腔內液體晃動將對航天器的姿態運動帶來強烈的擾動，這種影響的主要原因是推進劑大幅晃動將造成航天器整體的慣性特性顯著變化，同時產生較大的晃動擾動力和擾動力矩。這有可能引起航天器的結構破壞，甚至造成航天器姿態翻滾等嚴重后果，在工程實際中應設法解決或避免。

為此，初步設計了相應的姿態機動補償控制器：

同樣取kp=250,kd=2000，圖11為機動過程中相應的角速度響應。結果表明，該類控制器能很好地抑制航天器姿態角速度的振蕩，從而能有效避免實際工程中的潛在風險。

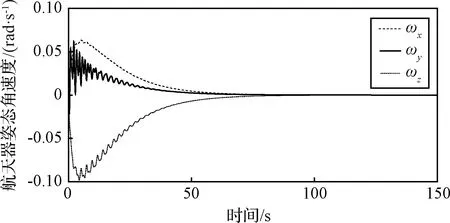
圖10 PD控制下三軸穩定姿態機動角速度響應Fig.10 Angular velocity response under PD controller

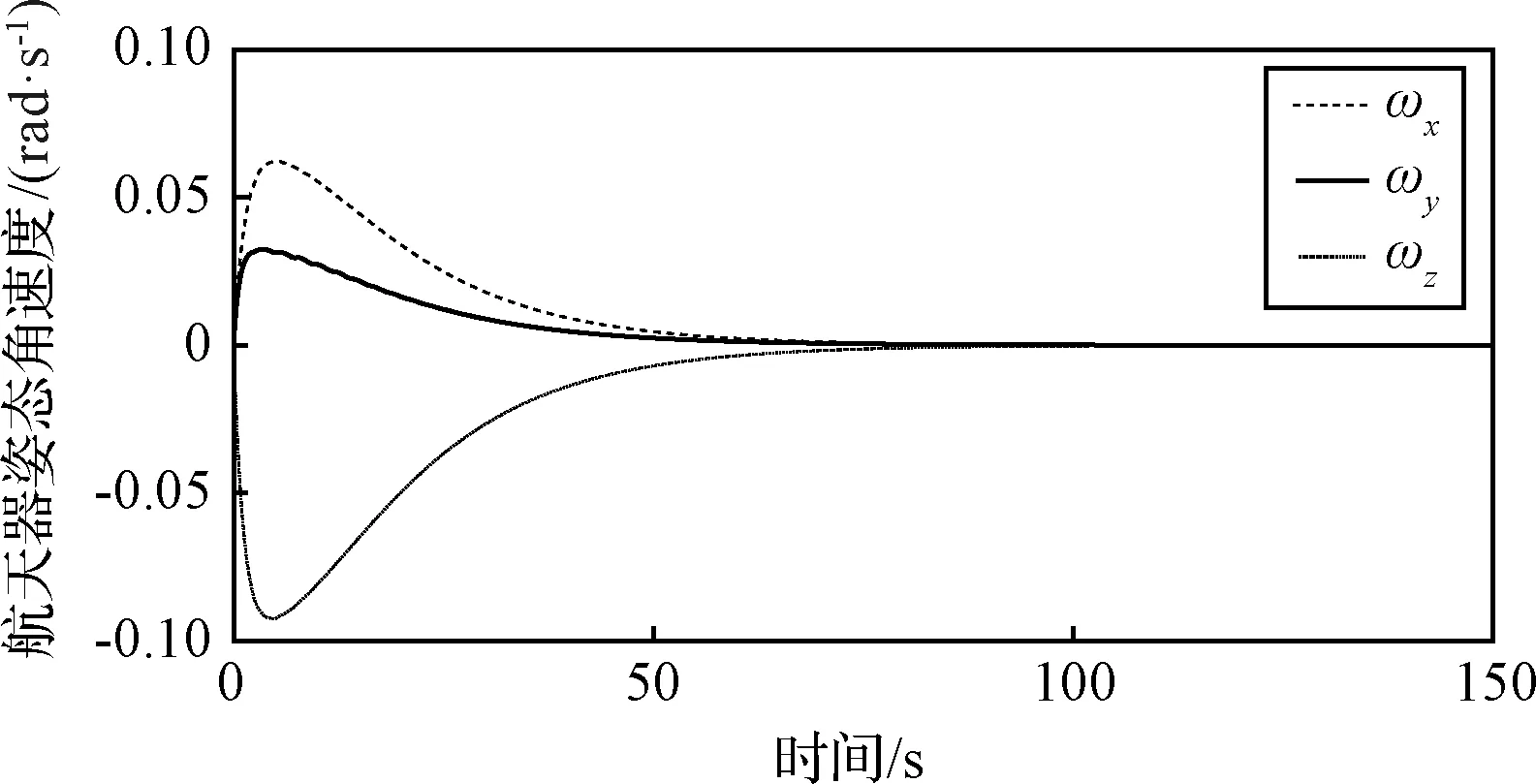
圖11 補償控制下三軸穩定姿態機動角速度響應Fig.11 Angular velocity under compensation controller

4 結 論

本文基于已有的質心面液體晃動等效力學模型，采用拉格朗日方法，系統地建立了計及航天器質心平動、姿態轉動與多貯腔內液體推進劑大幅晃動的剛-液耦合動力學精確模型。通過對比Flow3D求解所得的完全失重、復雜激勵下液體產生的晃動力及晃動力矩結果，驗證了所建模型的可靠性；同時，得到了特定工況下質心面模型等效摩擦特性系數與充液比之間的經驗關系，具體呈現為二次函數的近似關系。最后，基于本文中建立的耦合動力學模型，研究了該類航天器在進行三軸穩定姿態機動時的推進劑晃動與航天器主體姿態運動之間的動力學耦合特性，主要表現為推進劑大幅晃動造成航天器整體的慣性特性顯著變化，同時產生較大的晃動擾動力和擾動力矩，從而給航天器姿態運動帶來明顯的振蕩影響；為此，本文設計了一類抑制姿態振蕩的補償控制器，并且計算結果驗證了該控制器的有效性。