視覺測振技術在柔性太陽翼模態試驗中的應用
臧 旭,吳 松,郭其威,黃建民,宋漢文
(1. 復旦大學航天航空系,上海 200433;2. 上海宇航系統工程研究所,上海 201109;3. 同濟大學航空航天與力學學院,上海 200092)
0 引 言
柔性太陽翼發射前折疊收攏,入軌后通過中心伸展機構帶動柔性基板展開,具有頻率低、模態密集、阻尼特性復雜等動力學特性[1]。柔性太陽翼動力學參數是航天器姿態和振動控制系統設計中的主要參數,其準確性和可靠性對航天器在軌穩定運行具有重要意義[2]。有限元建模分析和模態試驗是獲取結構動力學特性的重要手段[3],柔性太陽翼結構復雜,有限元建模時采取大量等效和簡化,導致其參數辨識結果必然存在誤差。因此,模態試驗是準確獲取太陽翼動力學特性的重要途徑。傳統模態試驗(Experimental modal analysis,EMA)采用力錘及激振器作為激勵源,采用蜂蠟或膠水將力和加速度傳感器固定在被測結構表面,同時測量所施加的激振力和輸出響應,構造頻響函數,辨識結構模態參數[4]。
隨著機器視覺的迅速發展,視覺測振技術作為一種全新的非接觸、無損、全場測量手段,被廣泛運用于超低頻、大尺寸結構動態測試中[5],其具有高效、高精度、遠距離測量的特點。Laible等[6]利用發動機噴氣羽流對國際空間站2A太陽翼進行激勵,并通過兩臺相機獲取了太陽翼的在軌振動響應曲線。在超低頻大型航天器結構模態試驗中,激勵數據通常測量成本過高或根本不可測。工況模態辨識方法(Operational modal analysis,OMA)假設輸入為白噪聲,可僅依據輸出信號獲取結構動力學參數,是柔性機構地面模態測試及在軌參數辨識最常用的辨識方法,主要包括特征系統實現算法(Eigensystem realization algorithm,ERA)[7]、多參考最小二乘復頻域法(PolyMax)[8]等。
柔性太陽翼在軌處于真空、零重力環境,而地面模態試驗中空氣和重力的影響顯著且難以消除。本文針對柔性太陽翼地面模態試驗,通過基于視覺測振的OMA方法獲取太陽翼振動頻率、振型等動力學參數,并結合基于基恩士位移傳感器的EMA辨識結果及考慮地面模態試驗中空氣、重力影響的有限元分析結果,驗證了視覺測振模態辨識方法的有效性和準確性。
1 視覺測振技術
視覺振動測量中,圖像是振動測量信息的載體,本試驗基于圖像特征跟蹤法[9],為保證測量精度和可靠性在太陽翼上粘貼圓形反光標記(待測點),通過雙目CCD攝像機跟蹤太陽翼上圓形標記的位置變化信息,并對測量數據進行預處理,將被測物體的可視化圖像轉換為用于整翼模態辨識的振動信息。
1.1 圖像信息提取
圖1(a)為振動測量中的一副原始圖像,受輸入轉換器件及周圍環境等因素的影響,使圖像包含了一些背景和反光區,但從圖1(b)灰度直方圖可以看出原始圖像的灰度主要集中在30和180附近兩邊,即標記區域和其周圍背景的灰度相距較遠。為此本文采用固定的閾值變換對原圖像進行處理,即指定100為閥值,圖像中某像素的灰度值小于閾值,則將該像素的灰度值設置為0,否則設置為255,處理后的圖像如圖1(c)所示。
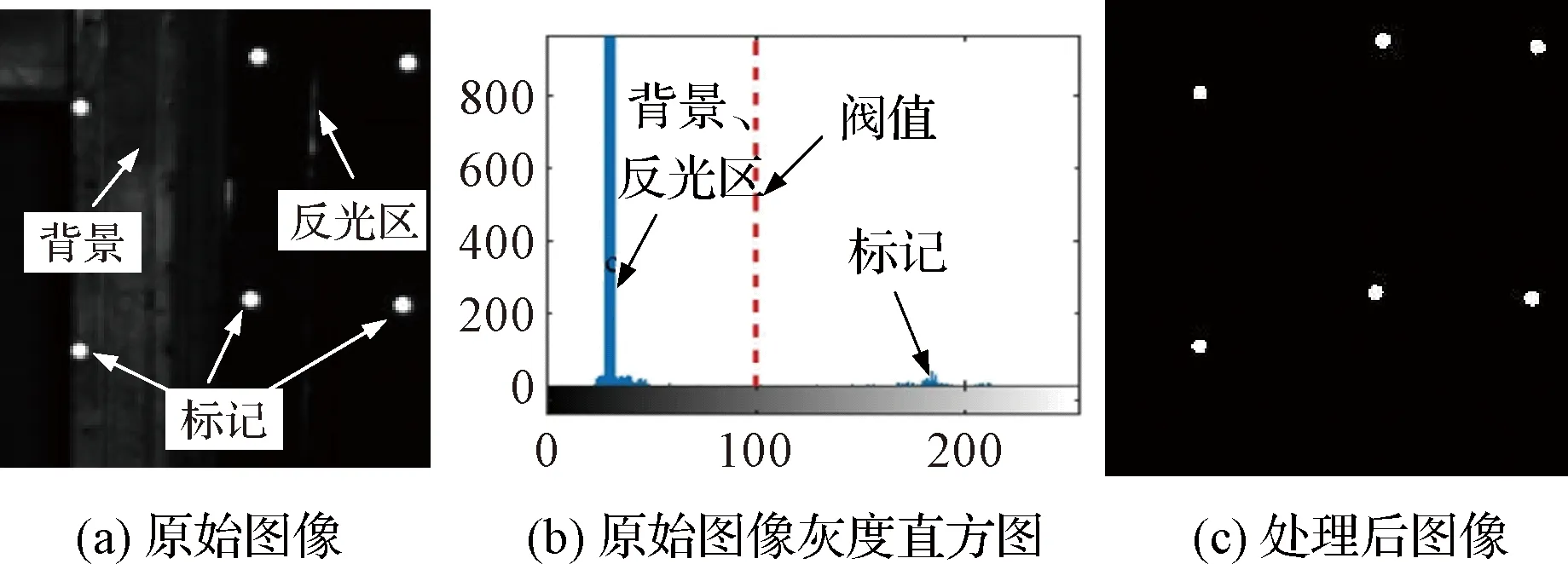
圖1 圖像處理過程Fig.1 Image processing process
將處理后圖像根據形心計算公式得到每幅圖像中光斑的形心位置(xc,yc),即可得到圓形反光標記的運動信息。圖像中光斑的形心位置(xc,yc)的計算式為:
(xc,yc)=
(1)
式中:f(i,j)為位于(i,j)位置的像素點的強度值,xij和yij為像素中心的x和y坐標值,M為行像素點的數目值,N為列像素點的數目值。相鄰兩幀圖像之間,待測點在x,y方向上的振動大小Δx和Δy分別為:
(2)
式中:x1,y1和x2,y2分別為振動前后兩幀圖像中光斑的形心位置。
1.2 三維空間坐標重建
在視覺測振中,每臺相機將被測物體的三維物理空間坐標反映在二維圖像坐標中,圖像承載了被測物體的所有信息。為獲取被測物體在物理空間中的振動信息,需同時利用兩臺相機對其進行拍攝。首先,根據視場內的固定靶點對相機主點坐標(圖像中心坐標)、焦距、比例因子和鏡頭畸變等內部參數,及相機像空間坐標系相對于世界坐標系的三維位置和方位關系等外部參數進行標定,獲取從圖像空間到物理空間的轉換關系,如圖2所示。
根據立體圖像中靶點、待測點和相機間的空間位姿關系,通過雙目多約束的聯合測量算法獲取被測物體的待測點在物理空間中的三維振動信息,其具體測量流程如圖3所示。
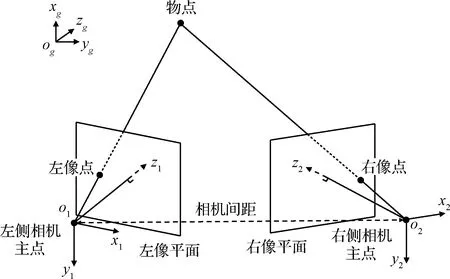
圖2 空間點三維重建Fig.2 Spatial point 3D reconstruction
1.3 位移數據零均值處理
圖像數據在經過繁瑣復雜的坐標系轉換后,最終得到每個待測點在空間絕對坐標下的振動位移數據。但這些位移數據具有一定的非穩態漂移和靜態變形如圖4(a)所示,不符合振動模態辨識中零均值數據的要求。經過簡單的零均值處理后,振動位移數據仍有較大幅值的零頻率信號,由于一般的濾波算法會造成一定的相位畸變,本文采用經驗模態分解(Empirical mode decomposition,EMD)法[10],將振動位移數據按頻率由高到低進行分解,使復雜信號分解成有限個本征模函數(Intrinsic mode function,IMF)(見圖4(b)),且每個IMF都滿足:1)函數在整個時間范圍內,局部極值點和過零點的數目必須相同,或最多相差一個;2)在任意時刻點,局部極大值的包絡(上包絡線)和局部最小值的包絡(下包絡線)平均必須為零。去除低頻的IMF分量,并將其它各階IMF進行求和,作為重構振動位移數據用于模態參數辨識。
2 柔性太陽翼地面模態試驗
為最大限度抵消重力對結構的影響,對太陽翼進行倒立垂直懸掛根部固定。試驗中在寬頻激勵下通過基于基恩士位移傳感器的EMA方法和基于雙目相機視覺測振的OMA方法進行模態參數辨識,兩種方法相互校驗,獲取太陽翼模態參數,試驗流程如圖5所示。
2.1 試驗方案及實施過程
參試柔性太陽翼由主框架和兩塊柔性陣面組成(見圖6(a)),整翼長度8 m,單塊柔性陣面尺寸為6.5 m×2 m,整翼寬度為5 m,除陣面外主體結構采用鋁合金材料,整翼總質量為175 kg。試驗時采用APS-110激振器,為太陽翼提供低頻大位移激勵,并在激振器頭部串聯一個力傳感器獲取試驗激勵數據(見圖6(c))。在太陽翼背面通過基恩士位移傳感器,獲取其振動位移數據(見圖6(d))。在太陽翼正面粘貼直徑20 mm的圓形反光標記,并通過兩臺Baumer TXG50 CMOS相機進行圖像采集,如圖6(b)所示。
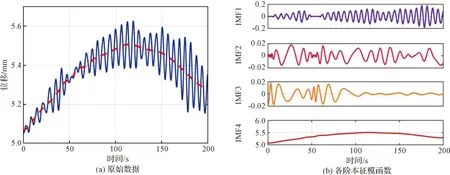
圖4 位移數據EMD分解Fig.4 The signal decomposition using EMD method
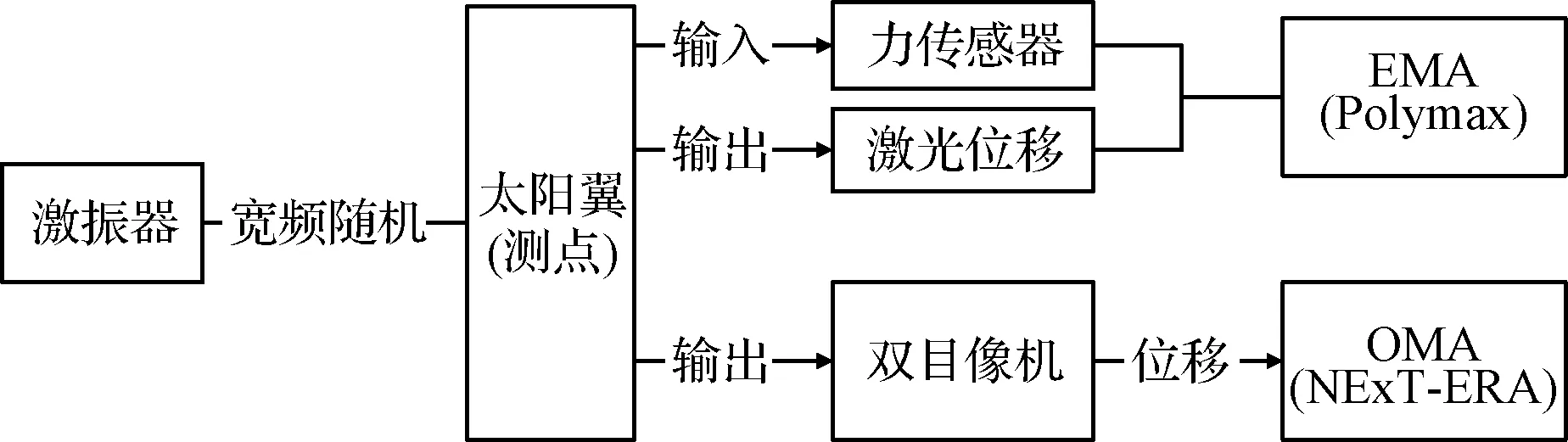
圖5 柔性太陽翼模態試驗流程圖Fig.5 Solar array modal test flow chart

圖6 試驗現場示意圖Fig.6 Test site diagram
試驗過程中通過11個基恩士激光位移傳感器對測點的位移響應信號和激勵力信號進行逐行采集,進而獲得其頻響函數,測點如圖7(a)所示;與此同時,兩臺相機對太陽翼上所有的測點進行同步采集,測點如圖7(b)所示。在激光位移傳感器獲得一行響應數據的同時,相機可采集太陽翼所有測點的響應數據。在完成一次完備的EMA模態分析試驗的同時,獲得了多組圖像數據,極大地提高了數據采集的效率。
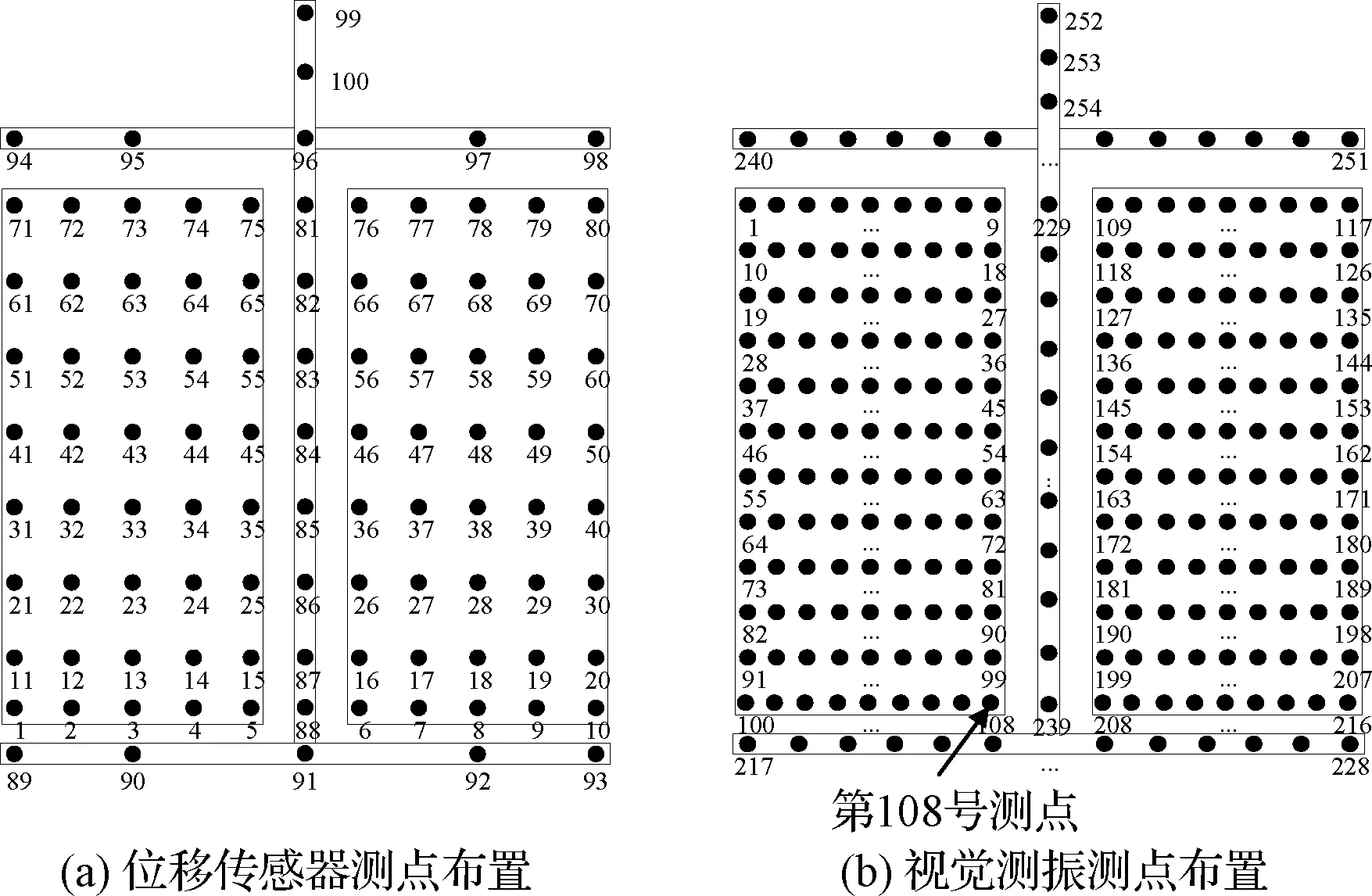
圖7 試驗測點布置圖Fig.7 The arrangement of the measurement points
2.2 測試數據預處理
從相機圖像中提取的各待測點位移原始數據是疊加了剛體位移后的絕對坐標,本文采用EMD分解對原始測試數據進行預處理,將其轉化為相對坐標下近似零均值的隨機位移數據。以太陽翼左側陣面右下角角點第108測點為例,具體位置如圖7(b)所示。
將第108測點原始數據進行EMD分解,分解后各階IMF時域和頻域功率譜密度(Power spectral density,PSD)曲線如圖8所示。去除后三階IMF,相當于執行了0~0.05 Hz的高通濾波,并將其它各階IMF求和作為濾波后的重構振動位移數據進行模態參數辨識,圖9為第108測點原始、重構和濾除數據的對比,重復以上步驟得到每個待測點在靜平衡位置處的零均值無相位畸變的振動位移數據。
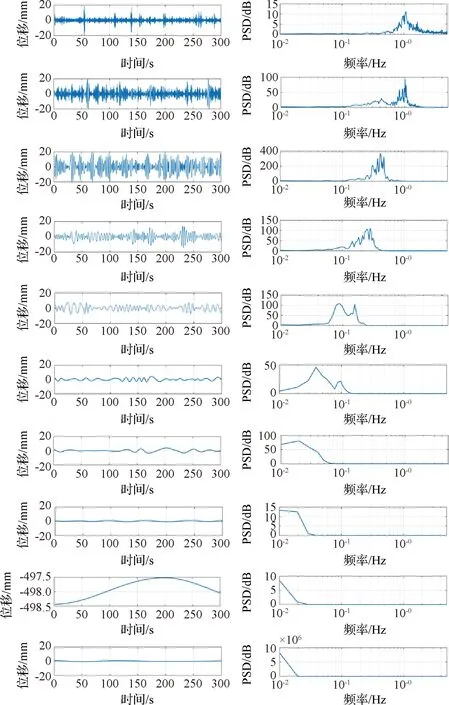
圖8 第108測點位移EMD分解(共10階,由上自下為1~10階。左側為時域;右側為頻域)Fig.8 The displacement signal decomposition using EMDmethod at point 108 (10 orders kept, from top to bottom: the1st~10th orders. Left: time domain; Right: frequency domain)
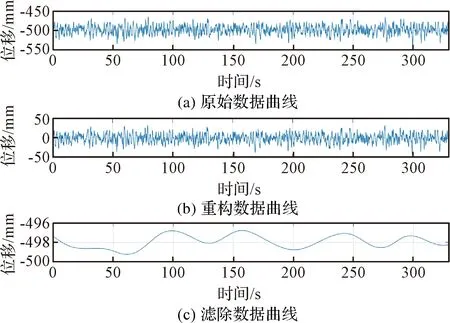
圖9 第108測點信號濾波效果Fig.9 Filter effect of displacement signal at point 108
2.3 模態參數辨識方法
模態參數辨識主要包括兩個部分:傳統試驗模態辨識部分(EMA法)、圖像采集信號的細化處理和僅由輸出響應的工況模態辨識部分(OMA法)。
1)EMA模態辨識
在太陽翼背面,通過11個基恩士位移傳感器,自上而下逐行對所有測點的位移響應信號進行測量,同步根據力傳感器獲取激勵信號,獲取所有測點的頻響函數。柔性陣面上測點的頻響函數如圖10所示,框架上測點的頻響函數如圖11所示,因試驗中2 Hz以后的頻響函數數值很小,故將頻響函數圖截取到2 Hz進行展示,并利用PolyMax法進行參數辨識[11]。
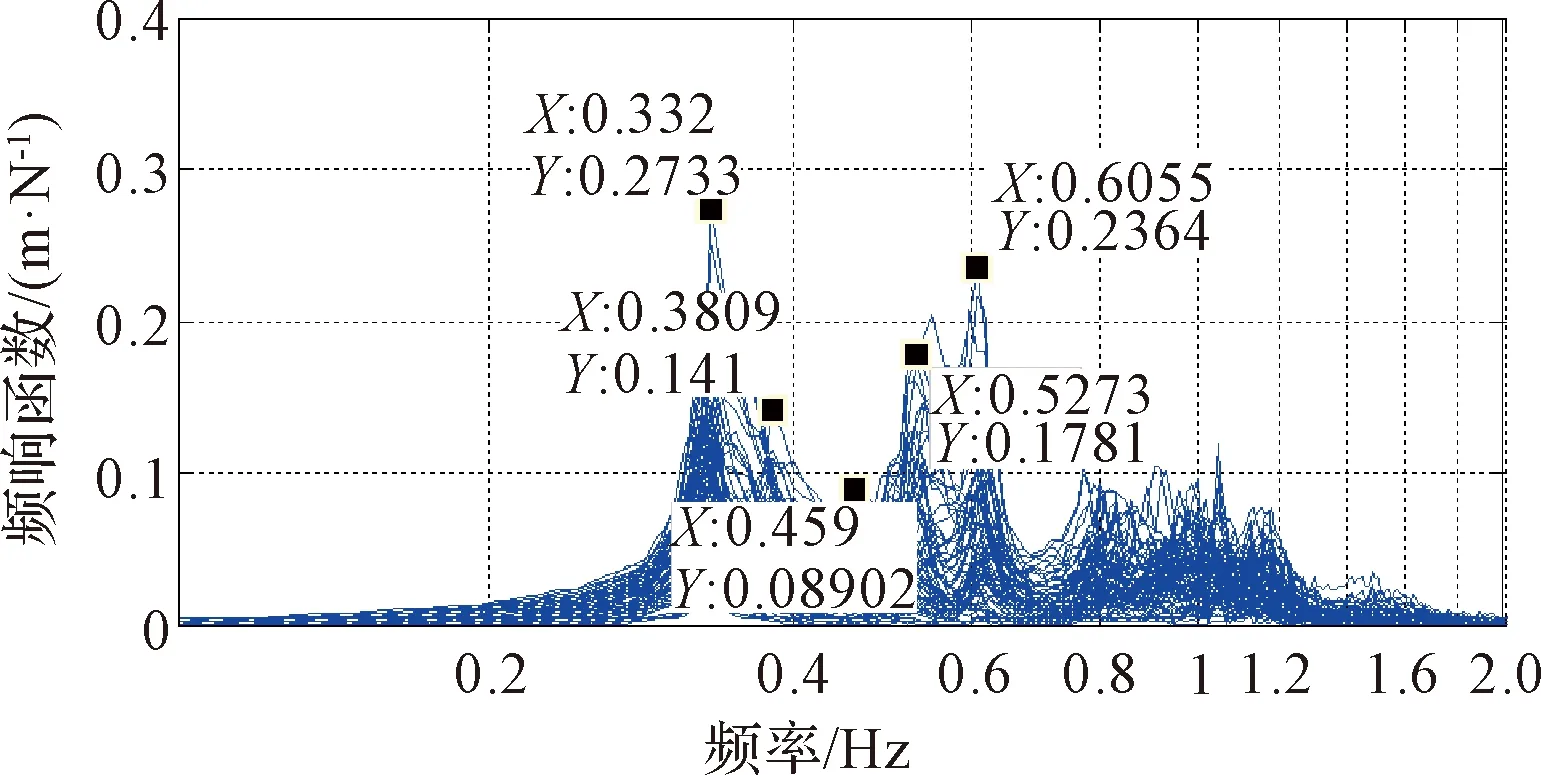
圖10 柔性陣面測點頻響函數Fig.10 Array points frequency response functions
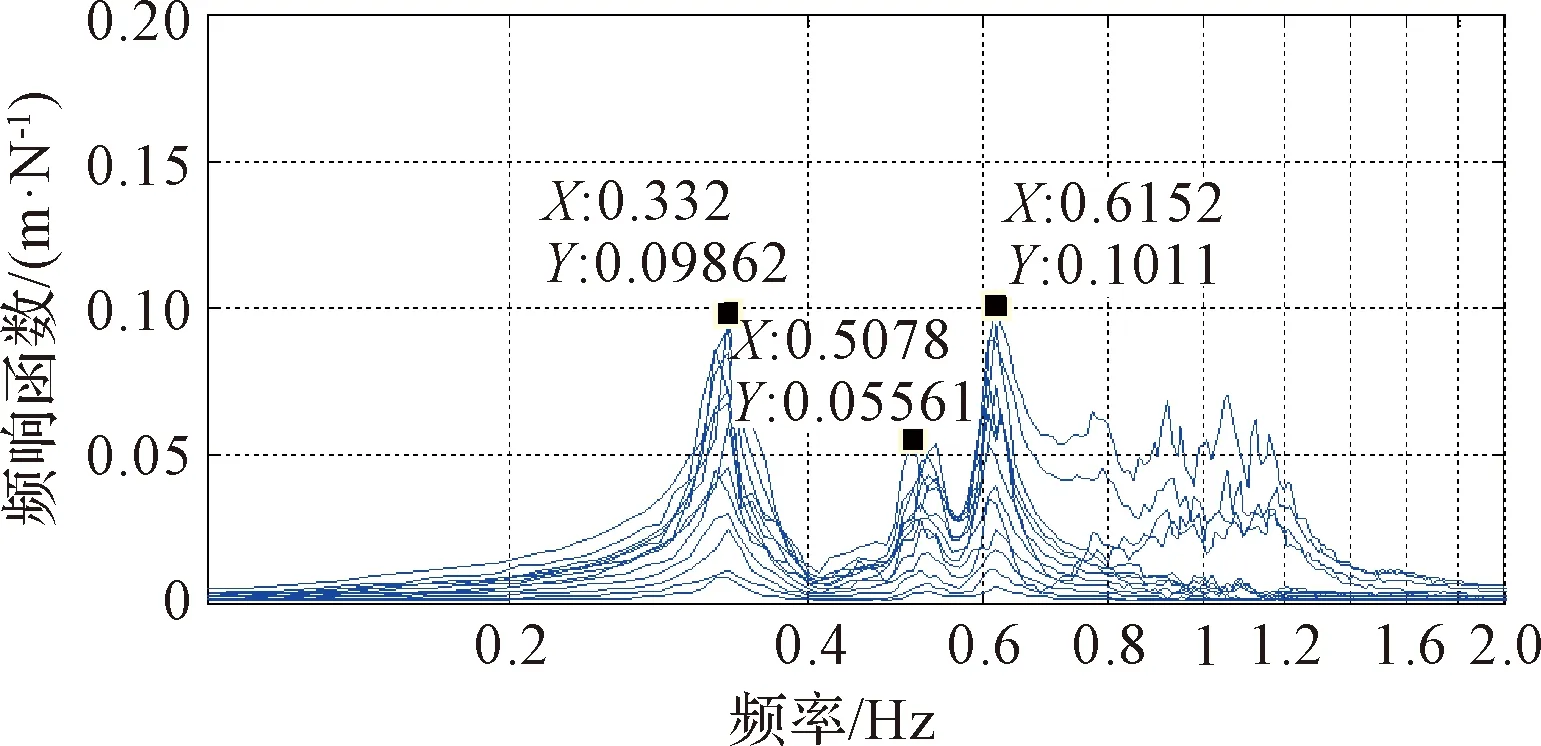
圖11 框架測點頻響函數Fig.11 Frame points frequency response functions
2)OMA模態辨識
試驗前先通過粘貼在固定工裝上的兩排靶點(見圖8(a))對相機的內部參數和外部參數進行標定。然后,在太陽翼正面通過雙目CCD攝像機跟蹤太陽翼上254個圓形標記的圖像信息,圖像采集頻率為10幀每秒。從圖像數據中提取所有待測點的位移響應初始數據,并通過EMD方法進行分解、重構,將原始數據轉換為靜平衡位置處的零均值振動位移數據。利用自然激勵技術(NExT)與特征系統實現算法(ERA)相結合的方法[12],先將處理后的振動位移數據進行相關計算,得到維數為254的相關函數矩陣R254×254,再通過自然激勵技術,任意一列相關函數等價于原系統在初始條件下的自由衰減響應,進一步利用相關函數代替自由衰減響應,輸入ERA算法進行模態參數辨識,具體過程如圖12所示。
2.4 試驗結果
基于基恩士位移傳感器的EMA方法和基于雙目相機視覺測振的OMA方法,辨識得到的柔性太陽翼前五階模態頻率如表1所示,前五階振型如圖13所示。從表1可以看出,基于雙目相機視覺測振的OMA方法的辨識結果與常規EMA方法的辨識結果一致度較高,各階偏差小于3.4%。
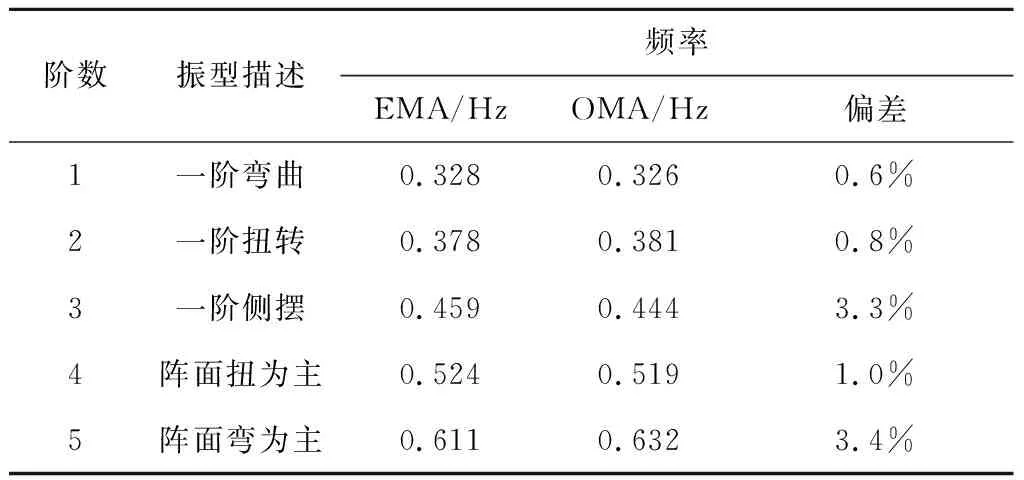
表1 柔性太陽翼前5階模態頻率Table 1 The first 5 natural frequencies by EMA and OMA

圖12 基于NExT-ERA算法的工況模態辨識流程Fig.12 OMA modal analysis procedure by NExT-ERA method
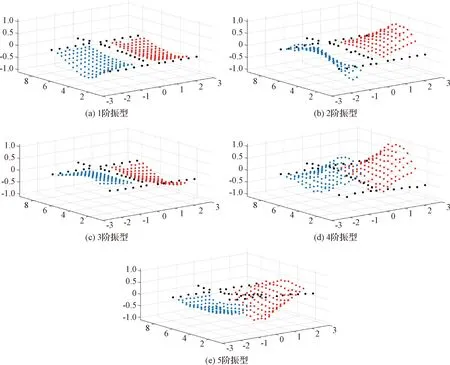
圖13 柔性太陽翼模態振型圖Fig.13 Modal shape diagram of solar array
3 柔性太陽翼模態數值仿真
利用有限元軟件MSC.PATRAN/NASTRAN建立柔性太陽翼有限元模型如圖14所示,其中主框架采用梁單元模擬,柔性陣面采用殼單元模擬,太陽翼張緊力通過間隙(Gap)單元施加在柔性陣面上。為準確模擬太陽翼地面模態試驗環境,須考慮空氣影響[13]及地面重力帶來的邊界效應影響[14]。
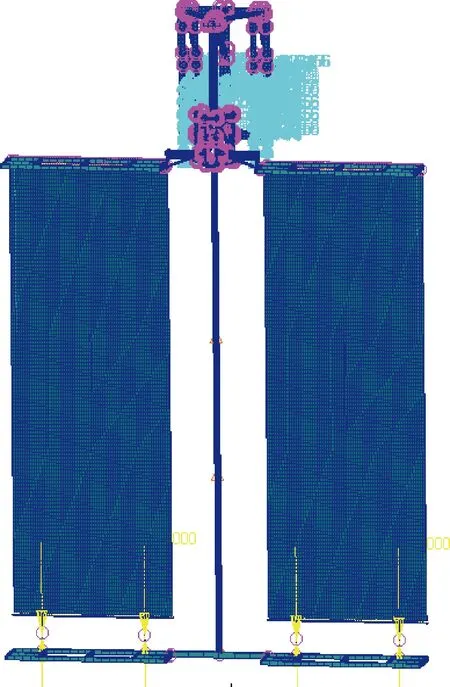
圖14 柔性太陽翼有限元模型Fig.14 Finite element modal of solar array
空氣的影響實質上是氣固耦合問題,由于空氣的附件剛度極小,因此其對太陽翼模態測試的影響主要表現為空氣附加質量導致測試頻率低于固有頻率。空氣影響可通過虛質量法進行仿真模擬,其預示結果如表2所示,空氣對柔性翼彎曲和扭轉頻率影響較大,其中一階彎曲模態頻率下降約24%,空氣對側擺頻率的影響可以忽略。

表2 空氣對柔性太陽翼模態頻率的影響Table 2 Influence of air on solar array modal frequency
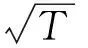
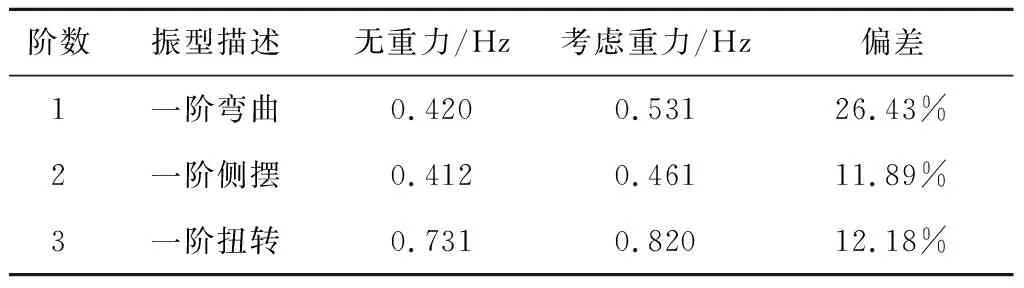
表3 重力對柔性太陽翼模態頻率的影響Table 3 Influence of gravity on solar array modal frequency
將同時考慮空氣及重力影響的柔性太陽翼模態分析結果與試驗結果進行對比,如表4~5所示。仿真分析頻率與基于基恩士位移傳感器的EMA方法和基于雙目相機視覺測振的OMA方法辨識頻率偏差均小于5%。
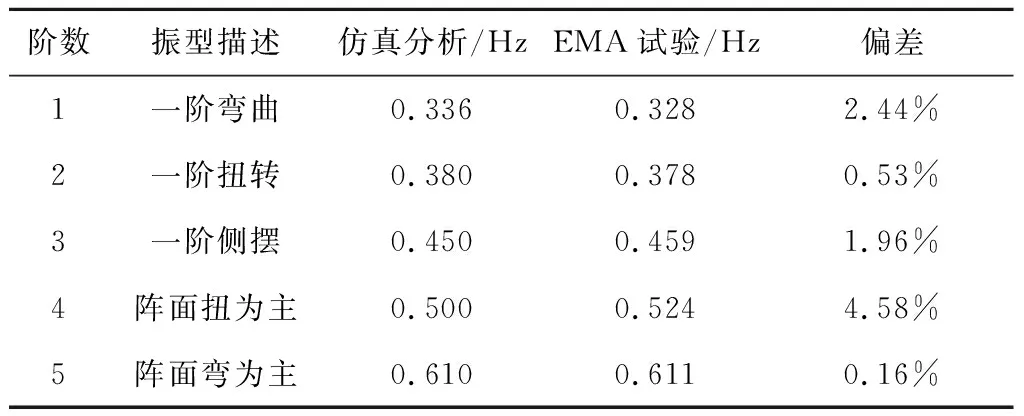
表4 柔性太陽翼仿真分析與EMA試驗頻率對比Table 4 Comparison of solar array’s simulation analysis andEMA test frequency
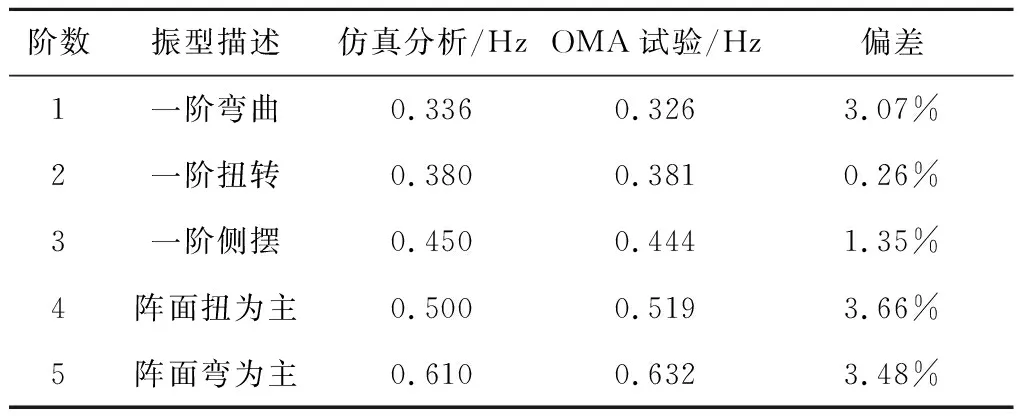
表5 柔性太陽翼仿真分析與OMA試驗頻率對比Table 5 Comparison of solar array’s simulation analysis andOMA test frequency
4 結 論
與傳統模態試驗方法相比,使用視覺測振技術測量結構振動信息具有非接觸、實時性強、精度高以及信息量大等顯著特點,本文通過兩臺CCD攝像機進行圖像特征跟蹤,并基于NExT-ERA算法的工況模態辨識方法,獲取了柔性太陽翼模態頻率、振型等動力學參數,結論如下:
1)基于雙目相機視覺測振的OMA方法模態試驗結果與基于基恩士位移傳感器的EMA方法試驗結果和有限元分析結果吻合較好,驗證了視覺測振系統的準確性、有限元建模的等效性及分析方法的有效性。
2)地面模態試驗中空氣及重力影響不可避免,地面模態試驗與有限元分析相互校驗是準確預示柔性太陽翼固有模態參數的重要途徑。

