自然形高空氣球上升過程形狀預測

楊澤川，羅汝斌，廖 俊，蔣 祎，袁俊杰，王 寧，李 珺

(1. 中南大學航空航天學院，長沙 410083；2. 北京宇航系統工程研究所，北京 100076)

0 引 言

高空氣球是一種可在臨近空間高度范圍工作、搭載多種任務載荷系統的多用途浮空平臺，具有駐空時間長、效費比高、安全性好等優點，在預警探測、偵察監視、導航通信等領域有廣泛的應用前景[1-2]。

高空氣球作為一種無動力浮空器，其動力學特性對于高空浮空器的快速部署至關重要。因此，很多學者針對高空氣球上升段動力學特性進行了研究。文獻[3]建立了氣球上升過程的運動模型和熱模型，計算了氣球上升的軌跡，并與飛行數據相比較，有較好的吻合。文獻[4]通過建立氣球上升過程中溫度微分方程和運動微分方程，運用兩節點模型計算了標準大氣模型下高空氣球的上升軌跡、上下表面及球內溫度變化等情況。文獻[5]采用大渦模擬的方法研究了不同球體間距對“球形囊體型”浮空器氣動特性的影響。文獻[6-7]精確模擬了高空超壓氣球的運動特性和熱力學特性，并分析了蒙皮膜的輻射特性和云對氣球熱力學的影響，研究不同大氣模型對高空氣球升空過程中的高度、氦氣溫度的變化曲線，分析了不同大氣模型對氣球熱動力學性能的影響。上述研究表明，在上升過程中，高空氣球的體積、速度等特性受到多因素的影響，進而影響浮空器的部署時間，因此，有必要針對浮空器上升過程中的體積以及速度等進行詳細研究。

文獻[8]對高空氣球上升階段與駐空過程中的動力學進行了仿真，上升速度曲線由于氦氣“超冷”現象呈現雙“V”形變化。文獻[9]仿真了零壓氣球的飛行軌跡，通過真實飛行數據驗證了仿真的正確，研究了影響氣球在漂浮區域高度穩定性的有效參數，對充氣量進行預測估計，使氣球在不需要壓艙物的情況下保持爬升的穩定性。文獻[10]建立了一種新的描述氣球熱力學和動力學特性的動態模型，分析了初始放飛條件對氣球飛行性能的影響，其中氣球的充氣量是影響上升速率最主要的因素。文獻[11]通過采用零壓氣球受力平衡方程分析了平流層高空氣球在升空過程中體積變化情況，并通過有限元方法驗證了數值計算的準確性，研究結果表明體積和充氦量是高空氣球的重要設計指標，其直接決定著高空氣球的升空高度與載荷攜帶能力。

研究高空氣球升空過程中的體積變化情況，對于高空氣球的總體設計具有重要的實用價值。氣球在上升過程中體積的增大會造成蒙皮應力的增大，不合理的氣球體積以及充氦量設計可能會導致氣球在上升階段就由于蒙皮的應力過大而撕裂[12]。針對自然形高空氣球，國內外諸多學者進行了氣球的形狀預測以及蒙皮應力情況的研究。明尼蘇達大學的研究者將氣球的形狀建模成一個非線性微分方程系統，這個非線性方程系統的解被稱為Σ形狀。文獻[12]使用該模型做了大量的數值計算，這些方程的邊界條件是基于有效載荷、氣球膜重量、體積和漂浮高度等。文獻[13]使用“平行打靶法”求解上升階段中對稱的自然形氣球非線性幾何方程，該方法假設氣球由圓錐體和一個固定角組合而成，并且氣球蒙皮上沒有周向應力，證明了“平行打靶法”可以很好地求解Σ形狀等式。文獻[14]構造了“切向增量法”，將氣球的加強頭部層考慮進模型，忽略蒙皮的彈性形變和褶皺，成功地預測了不對稱氣球在漂浮階段的形狀，與“平行打靶法”的結果很好地吻合。

對于氣球形狀的研究，Frank baginski提出氣球系統的能量最小并且滿足材料的約束，通過這種方法得到的氣球形狀叫做EM形狀(Energy Minimizing Shape)[15]。文獻[15-16]根據氣球系統的能量最小化原理，將氣球實際觀察中的特征(如褶皺等)考慮進模型，對上升階段高空氣球的軸對稱形狀、非對稱形狀進行建模，模型的計算結果能夠很好地反映氣球形狀，并且還利用“差分原理”計算氣球形狀，發現該方法計算的對稱EM形狀與求解標準Σ形狀能很好地吻合；而對于不對稱形狀氣球，該方法計算出的氣球形狀與實際觀察中出現的氣球形狀特征很接近。文獻[17]基于殼體有限元法對科學氣球進行結構分析，分析了科學氣球不同飛行高度下外形和蒙皮應力分布情況。

國內方面，文獻[18]通過推導考慮多種因素的一般球形理論得到了地面不同充氣體積下球體的二維形狀，對不同因素在球形設計過程中的影響進行了詳細的分析，并設計了地面試驗驗證氣球形變和應力分析數值結果。文獻[19]采用有限元方法，通過選擇適當的單元算法、接觸算法和流固耦合參數，初步給出了半充氣自然形球體形狀。文獻[20]通過考慮大氣環境因素和浮升氣體溫度的影響，簡單預測了氣球在地面和漂浮高度的幾何外形和蒙皮張力。文獻[21]利用肥皂泡理論分析氣球膨脹的全過程，通過最小能量理論進行應力分析和剪裁設計，對氣球不斷上升過程中體積擴大、增加內壓過程進行研究，分析其形狀變化和膜應力變化特征。

自然形高空氣球在上升過程中體積隨上升高度的增加而變化，這是由于外界大氣溫度、密度和壓力隨上升高度的增加而變化，氣球受到的熱輻射影響氣球內浮升氣體的溫度，導致氣球內浮升氣體壓力的變化和氣球膜內外壓差的變化，氣球的幾何外形隨壓差的變化而改變。實際上，氣球的蒙皮應力由氣球的曲率半徑決定，因此需要準確且可靠的理論方法來預測氣球上升過程的蒙皮應力，本文考慮氣球在上升過程中的熱輻射，利用最小勢能法通過數值迭代計算了自然形氣球在上升過程中的形狀和應力情況，研究了浮升氣體充氣量、氣球內外溫差對氣球形狀和應力分布的影響。該方法簡潔方便，且可獲得較為精確的預測結果，為高空氣球的工程應用及概念設計等問題奠定基礎。

1 理論模型

1.1 氣球熱力學模型

根據熱力學方程，氣球內部浮升氣體的體積及壓力都受到氣體溫度的影響。為了研究高空氣球形狀以及蒙皮應力狀況，有必要針對高空氣球的熱特性進行分析。高空氣球在升空過程中，外部受氣體對流、太陽輻照、地面紅外輻射等多種環境熱流因素的影響，內部受蒙皮內表面間的輻射換熱、表面自然對流換熱等因素影響[22]，內、外熱環境通過蒙皮進行耦合換熱，引起氣球溫度場的瞬態非均勻變化。本文在分析平流層熱環境的基礎上，考慮高空氣球內部浮升氣體溫度受多種輻射熱源以及表面對流等復雜因素影響[23]，建立了高空氣球的熱力學模型，研究了浮升氣體的熱性能。

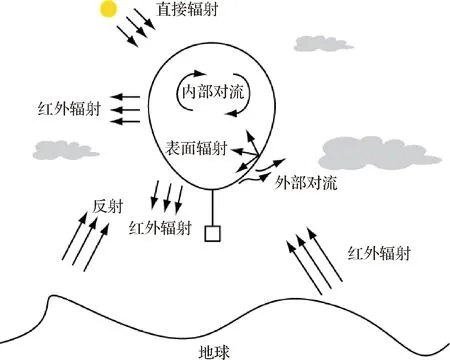
圖1 高空氣球熱環境因素Fig.1 Thermal environment of the high altitude balloon

高空氣球的各個部分受到不均勻的太陽輻射，將氣球蒙皮劃分成小網格，由N個灰體表面組成封閉系統，則蒙皮單元的穩態平衡方程為：

qout,ab-qout,em+qin,ab-qin,em+qcv,ex+qcv,in=0

(1)

式中：qout,ab為蒙皮單元外表面吸收的輻射熱流，qout,em為蒙皮單元外表面發射的輻射熱流，qin,ab為蒙皮單元內表面吸收的輻射熱流，qin,em為蒙皮單元內表面發射的輻射熱流，qcv,ex為蒙皮單元外部對流，qcv,in為蒙皮單元內部對流。

蒙皮單元外表面吸收的輻射熱流qout,ab=qs+qAlb+qAms+qIR,e。其中，太陽直接輻射熱流qs為：

qs=αsτsEscosβ

(2)

式中：αs為蒙皮外表面對太陽光的吸收率，τs為大氣對太陽輻射的透射率，Es為太陽常數，取值1358 W/m2[8]，β為蒙皮單元外法線與太陽光線的夾角[24]。

大氣對太陽輻射的透射率τs為：

τs=(e-0.65ν+e-0.95ν)/2

(3)

式中：ν為空氣質量比。

反照輻射熱流qAlb為：

qAlb=σfρeIAlbsinθ

(4)

式中：σf為指示因子，白天取值為1，夜晚取值為0，ρe是地球反照率，IAlb為地面反射輻射強度，具體計算見文獻[25]，θ為光線與地平線的夾角。

大氣散射輻射熱流qAms為：

(5)

式中：α為太陽高度角，φ為蒙皮面單元法向量與重力方向的夾角[25]。

地球紅外輻射熱流qIR,e為：

qIR,e=αexτairqeFw,e

(6)

式中：αex為蒙皮外表面紅外輻射吸收率，與蒙皮外表面的發射率相等，τair為空氣紅外透射率，qe為地球紅外輻射熱流，取值為220 W/m2[24]，Fw,e為蒙皮表面對地球的角系數。

蒙皮單元外表面發射的輻射熱流qout,em為：

(7)

式中：εex為蒙皮外表面發射率，σ為波爾茨曼常數[25]，Tair為外界大氣溫度，εsky為天空發射率，具體計算見文獻[22]。

對于蒙皮內表面單元i，其發射的輻射熱流qin,em為：

(8)

式中：εin為蒙皮內表面發射率，Xi,j為微元面i對微元面j的角系數，見參考文獻[26]，qin-j,em為蒙皮內表面單元j發射的輻射熱流。

蒙皮單元內表面吸收的輻射熱流qin,ab為：

(9)

蒙皮單元外部對流qcv,ex為：

qcv,ex=hex(Tair-Tfilm)

(10)

蒙皮單元內部對流qcv,in為：

qcv,in=hin(Tgas-Tfilm)

(11)

式中：hex為該蒙皮單元外表面與氣流的對流換熱系數，hin為該蒙皮單元內表面與高空氣球內部浮升氣體的自然對流換熱系數，Tgas為高空氣球內部浮升氣體溫度。

蒙皮單元外表面與氣流的對流換熱系數hex為[24]：

(12)

式中：Re為雷諾數，Prair為空氣普朗特數，λair為空氣導熱系數，L為高空氣球特征長度。

蒙皮單元內表面與高空氣球內部浮升氣體的自然對流換熱系數hin為[25]:

hin=C(Gr·Prgas)nλgas/L

(13)

式中：C，n為常數[25]，Gr為格拉曉夫數，Prgas為浮升氣體普朗特數，λgas為浮升氣體導熱系數。

(14)

式中：ρgas為浮升氣體密度，g為重力加速度，μgas為浮升氣體動力黏度，R0為氣球半徑。

高空氣球內部浮升氣體平均溫度Tgas的控制方程為：

(15)

式中：cgas是浮升氣體的比熱容，Mgas是浮升氣體的質量，S為氣球整個表面，dA是高空氣球蒙皮單元面積。

1.2 氣球幾何外形

由于氣球囊體材料具有非線性、黏彈性、各向異性和不能抗壓等特點[27]，當氣球部分填充浮升氣體時，氣球的底部形成復雜的非軸對稱的褶皺部分，而對于氣球上部分，基本呈軸對稱形式[14]。在之前的氣球研究中，自然形氣球研究普遍采用的優化方案是基于以下假設[18]：(1)關于中心軸軸對稱；(2)圓周應力為零；(3)蒙皮材料不能伸長。本文對于自然形氣球采取上述假設(1)和(3)，對于在沒有攜帶載荷情況下的軸對稱氣球，它的幾何形狀可以看成一個半徑為R0，球心為C0的球體；而當氣球在攜帶載荷的情況下，氣球趨于一個球-圓錐體，由球體與圓錐體相切組成[20]，如圖2所示。

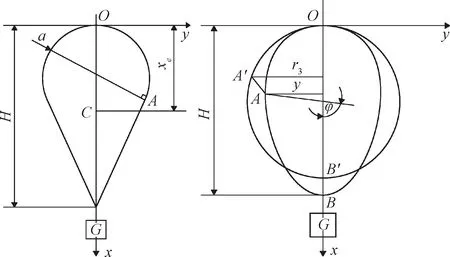
圖2 氣球坐標示意圖[23]Fig.2 Balloon coordinate diagram

可以將氣球的剖面曲線寫為：

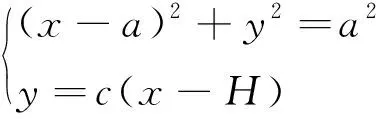
(16)

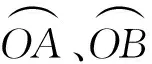
因此，在經向方向材料約束方程寫為：

(17)

(18)

同時還有幾何關系：

(19)

將氣球剖面曲線代入到材料的約束方程(17)、(18)，就能得出切點A的位置yA，xA，氣球質心的位置xC，氣球的豎直方向的總長度H，以及上半部分球的半徑a，從而得到氣球的體積為：

(20)

1.3 最小勢能法

最小勢能原理是指在所有可能的變形中，其實際存在的變形使得物體的總勢能取最小值[28]。氣球系統的總勢能由兩部分組成，一部分是氣球系統的重力勢能，另一部分是浮升氣體的壓力勢能。

通過簡化模型，氣球系統的重力勢能由浮升氣體的質量，氣球蒙皮的質量以及攜帶載荷的質量產生，表達式為：

E=-(Mgas+m0)gxC-mGgH

(21)

式中：m0為氣球蒙皮的質量，mG為氣球攜帶載荷的質量；xC為氣球系統的質心的坐標。

根據氣球系統的受力平衡，就能得到浮升氣體的質量：

Mgas=Vρ-(m0+mG)

(22)

式中：ρ為外界大氣的密度。

浮升氣體的壓力勢能表達式為：

W=Δp·V·lnV

(23)

其中，Δp為球內外的壓差，根據理想氣體狀態方程，可以得到Δp為

(24)

式中：Rmix為浮升氣體常數，p2為氣球外部大氣壓強。

氣球系統的總勢能為：

Π=W+E=Δp·V·lnV-

((Mgas+m0)gxC+mGgH)

(25)

將氣球的幾何外形方程求得的參數代入到總勢能方程中，這樣式(25)就是關于參數c的表達式，通過求得總勢能的最小值，就能解得參數c，求得相應的氣球剖面曲線，就能得到不同高度的氣球形狀。

1.4 蒙皮應力

通過簡化模型，不考慮氣球在上升過程中出現的褶皺、多余材料等造成氣球水平剖面半徑變化，氣球需要滿足材料在圓周方向的約束。應力分布情況如圖3所示。

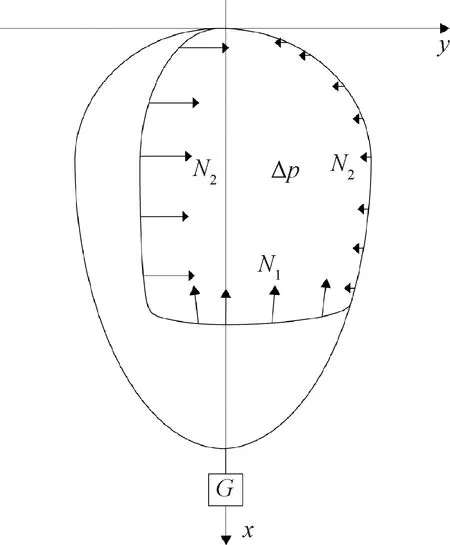
圖3 氣球應力示意圖Fig.3 Balloon stress schematic

因此，經向應力N1的平衡方程為：

2πr3N1sinφ=Δpπy2+G

(26)

2πr3是氣球在沒有承受載荷時水平剖面周長，G為氣球豎直方向的重力。簡化方程(26)，得到：

(27)

同理，分析氣球豎直剖面，氣球的緯向應力N2為：

(28)

故經向應力N1、緯向應力N2為關于y，r3和φ的表達式，y和r3的關系由材料的經向約束方程(17)、(18)得到，因此，只要求得氣球的形狀就能得到氣球的經向應力和緯向應力。

2 算例結果與分析

2.1 計算實例

由上述所建立的模型，編寫高空氣球上升過程的數值仿真程序，整個仿真程序的結構如圖4所示。本文所用的高空氣球規格參數，基本參數見表1[20]。

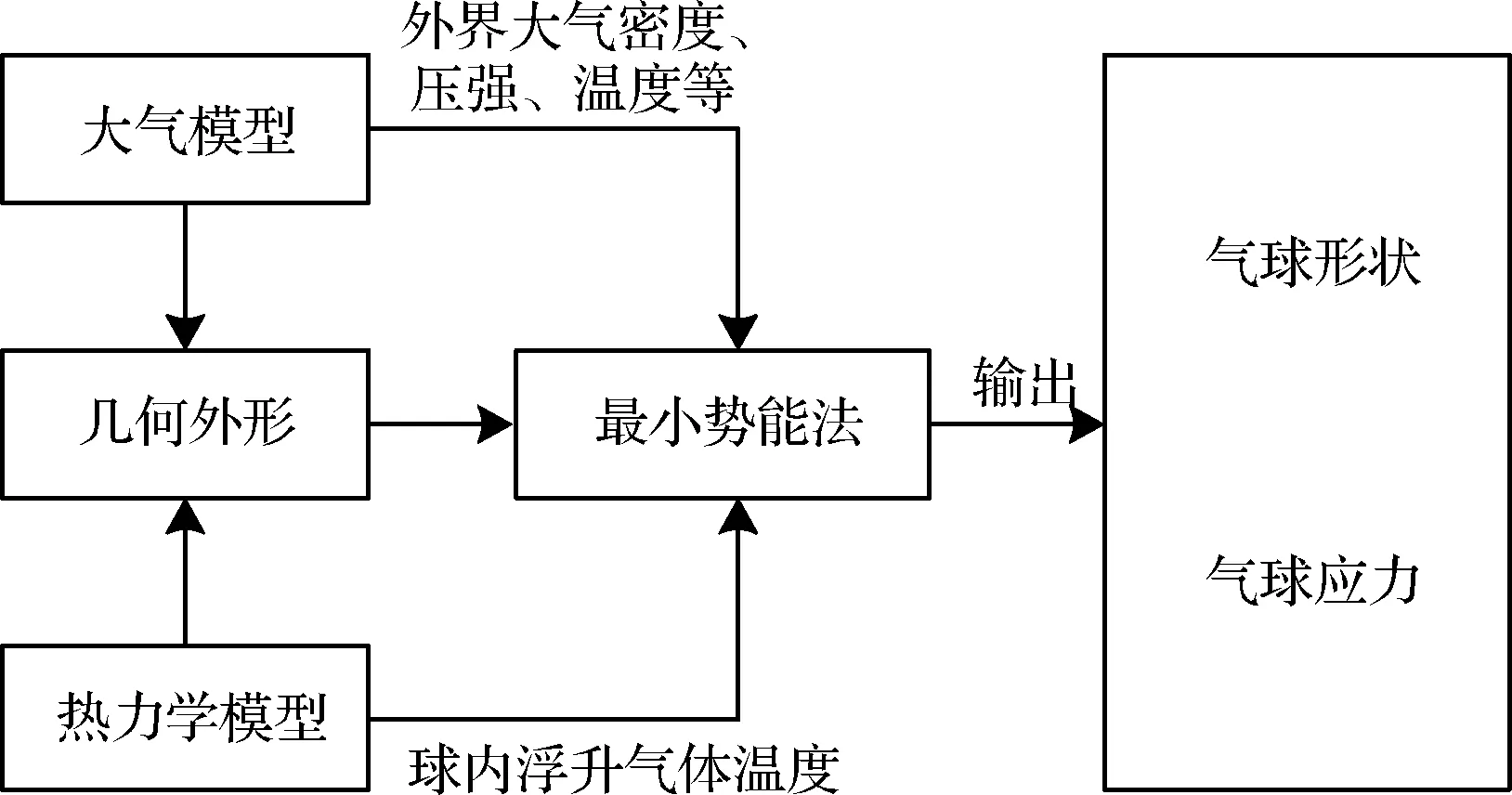
圖4 仿真程序結構圖Fig.4 Simulation program structure

表1 氣球系統參數[20]
Table 1 Balloon system parameters

參數值氣球初始半徑R0/m17.5氦氣氣體常數Rmix/(J·kg-1·K-1)1511.4載荷重量G/N10520氣球蒙皮重量m0g/N4618 氣球蒙皮厚度/mm0.12 蒙皮面密度/(g·m-2)120

2.2 仿真結果

2.2.1模型校驗

為了校驗以上提出的高空氣球熱力學模型，將仿真結果與文獻[25]中的結果進行對比，采用文獻[25]中的超壓氣球物性參數，分析氣球在抵達31.5 km左右高度時的內部浮升氣體溫度變化，可以得到圖5。上午6時之前氦氣溫度維持在240 K左右，隨后開始上升，中午12時達到最大，隨即下降，該模型計算結果與對比值最大相差0.5 %，與文獻[25]中結果吻合較好。

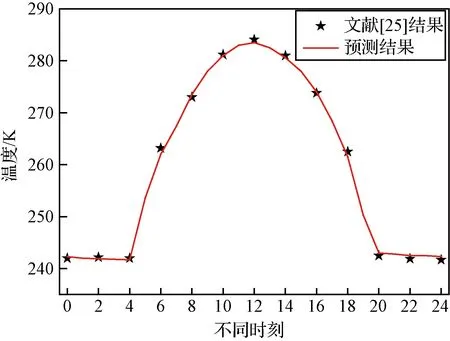
圖5 不同時刻氦氣平均溫度Fig.5 Average temperature of the helium at different times

選用Wen等[14]所設計的氣球的參數，利用最小勢能法和文獻中所計算的應力情況進行對比，驗證簡化幾何模型下的最小勢能法結果的準確性。

表2 氣球參數[14]Table 2 Balloon parameters

圖6展示了利用表2氣球參數經過最小勢能法計算氣球的應力情況與文獻[14]的結果進行對比，文獻[14]選取浮力系數為0.06，利用最小勢能法得到的氣球經向應力N1可以吻合文獻[14]的計算結果。

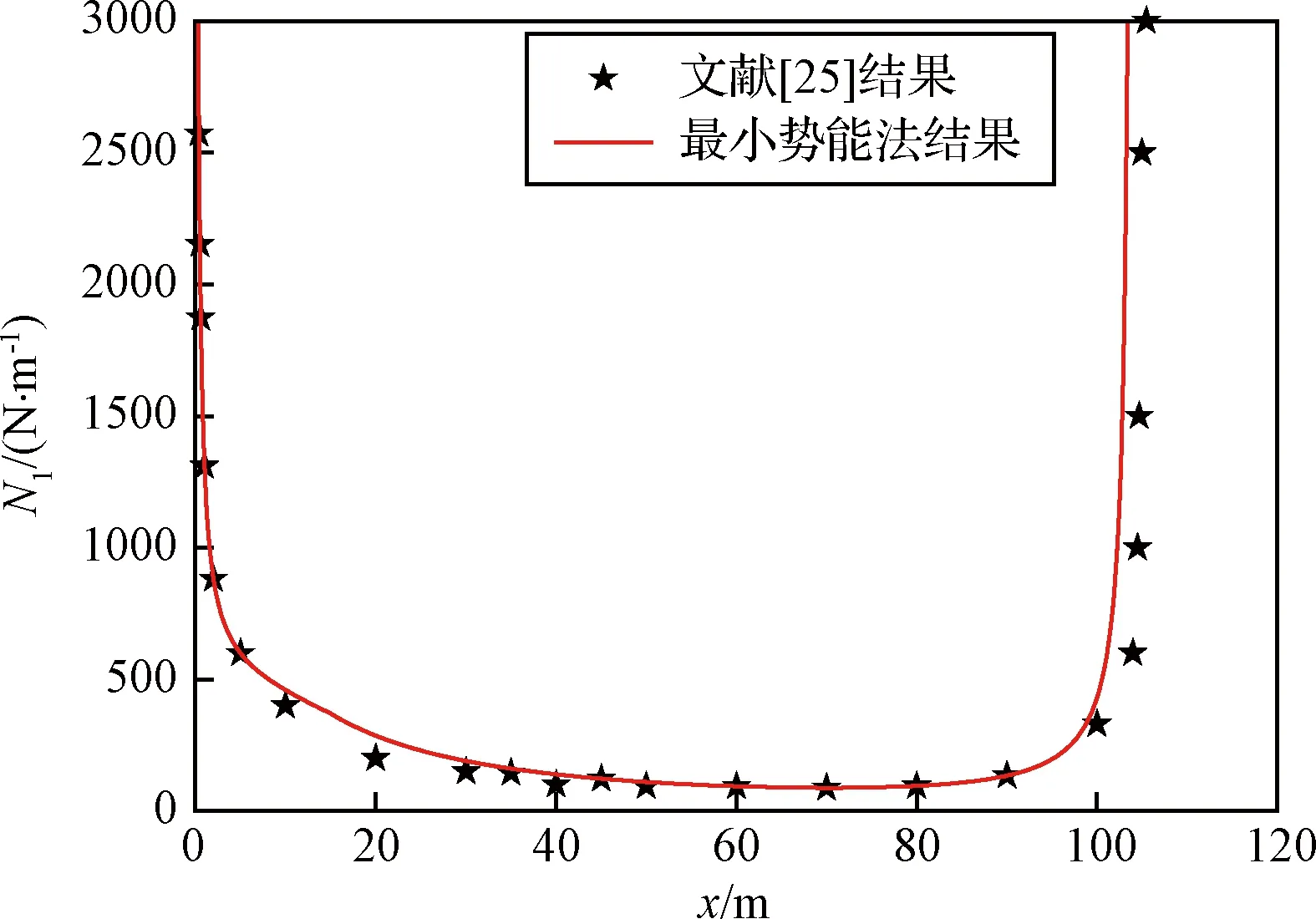
圖6 蒙皮應力對比圖Fig.6 Comparison of film stress

2.2.2上升過程氣球形狀及應力

將氣球參數代入到氣球熱力學模型中，可得到氣球在上升過程中不同高度的內部氦氣溫度Tgas，再將氣球系統的各項參數代入到氣球總勢能表達式(25)中，通過求氣球總勢能的最小值，得到氣球上升過程中不同的c值，確定氣球上升過程中的形狀及應力。圖7是氣球在上升過程中的形狀，隨著高度的增加，c值逐漸增大，氣球下部分的圓錐體的母線越來越平緩，氣球由開始的水滴形逐漸變化成球形。

圖7 不同高度氣球形狀圖Fig.7 The balloon shape at different height

圖8是上升過程中蒙皮的經向應力N1的變化曲線。圖9是上升過程中蒙皮的緯向應力N2的變化曲線。經向應力N1比緯向應力N2的數量級大，因此，很多自然形氣球的應力分析時忽略緯向應力。經向應力N1呈現“馬鞍”形，氣球的頂部和氣球的底部經向應力與氣球中間部分的經向應力相差很大，在現在的氣球設計過程中，氣球頂部和氣球底部都加多層蒙皮材料來承受氣球的經向應力；氣球的緯向應力N2與經向應力N1分布不同，氣球的緯向應力N2的極值在氣球的半徑最大處，并且數值很小，在上升過程中隨高度的增加，緯向應力N2逐漸減小。

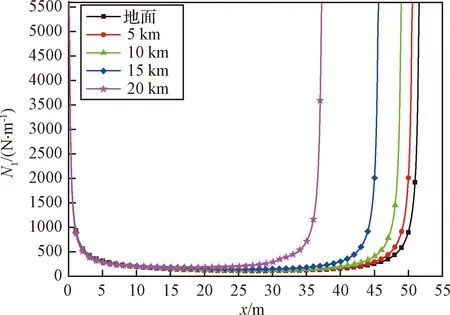
圖8 上升過程氣球經向應力圖Fig.8 Balloon meridional direction stress curves duringthe ascent

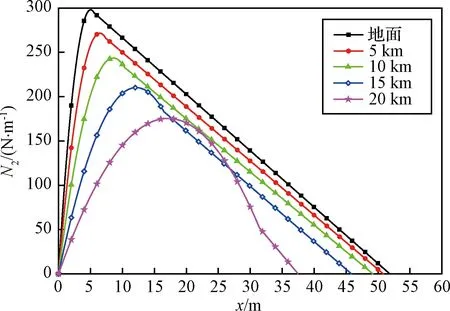
圖9 上升過程氣球緯向應力圖Fig.9 Balloon circumferential direction stress curvesduring the ascent

2.2.3不同充氣量的氣球形狀及應力分布

選取氣球在03:00時的準穩態計算氣球在不同充氣量下氣球形狀和經向應力N1的分布情況，氣球的充氣量由氣球所攜帶的載荷決定，本文選取相差200 kg的5個載荷量，為252～1052 kg之間，分析在20 km漂浮下氣球的形狀及經向應力N1分布情況，如圖10、圖11所示。

圖10是氣球在不同充氣量下20 km氣球的形狀，隨著氣球攜帶載荷量的增加，氣球上半部分圓球體的半徑a變大，而氣球整個豎直長度H變小，而出現變化的位置位于圓球體與圓錐體相切點，攜帶載荷量大的氣球下部分的圓錐母線斜率較小，導致氣球豎直長度H變小，攜帶載荷量小的氣球下部分的圓錐母線斜率較大，導致氣球豎直長度H變大。

圖11是氣球在不同充氣量下20 km的經向應力N1分布情況，在不同的充氣量下，經向應力N1服從“馬鞍”形分布，在氣球的頂部和氣球的底部較大，氣球中間部分數值較小，在本文選取的充氣量中，氣球的頂部部分應力大小基本相同，而區別出現在氣球的底部，氣球的經向應力N1急劇上升到最大，且底部的最大值與氣球攜帶的載荷量的大小有關，載荷越大，氣球底部的應力值越大，氣球膨脹得越厲害，氣球容易破裂。

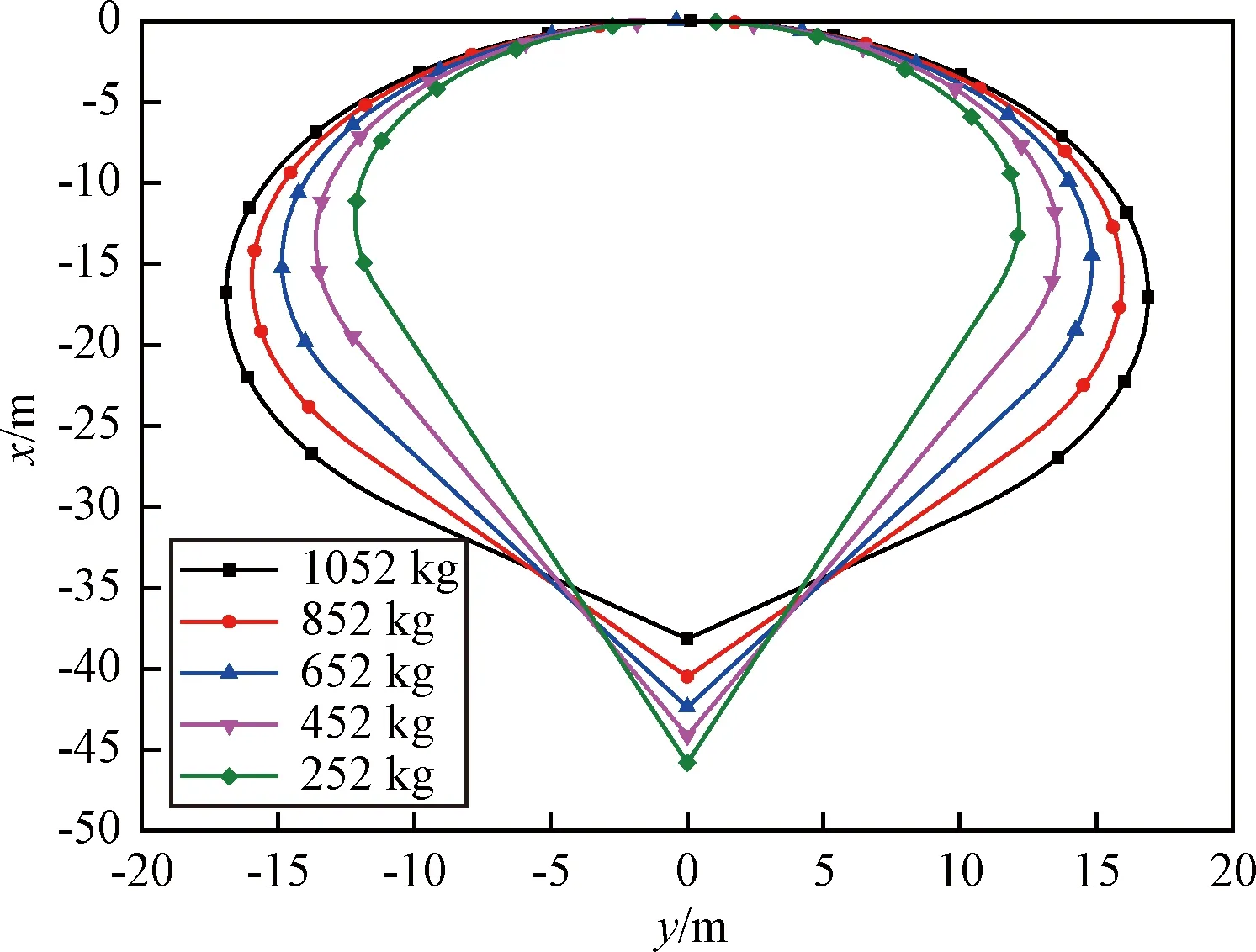
圖10 不同載荷量下氣球形狀圖(20 km)Fig.10 Balloon shape under different load (20 km)

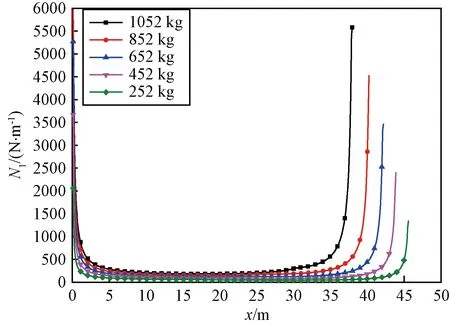
圖11 不同載荷量下氣球經向應力圖(20 km)Fig.11 Balloon meridional direction stress curves underdifferent load (20 km)

2.2.4不同時刻的氣球形狀及應力分布

選取氣球攜載1052 kg在不同的時刻下計算氣球在20 km的形狀及應力分布，在不同的時刻下根據熱力學模型計算得到球內外溫差，球內外溫差的不同導致球內外壓差的不同，壓差使得氣球的形狀及應力分布規律不同。

圖12是不同時刻下20 km氣球形狀圖，在20 km高度時，氣球內外溫差受太陽輻射影響隨時刻變化，氣球形狀也隨溫差發生變化，溫差越小，氣球越圓，呈球形；圖13是不同時刻下20 km氣球經向應力N1分布情況，在20 km不同時刻下，氣球頂部和中部經向應力N1大致重合，在氣球的底部經向應力N1出現不同。

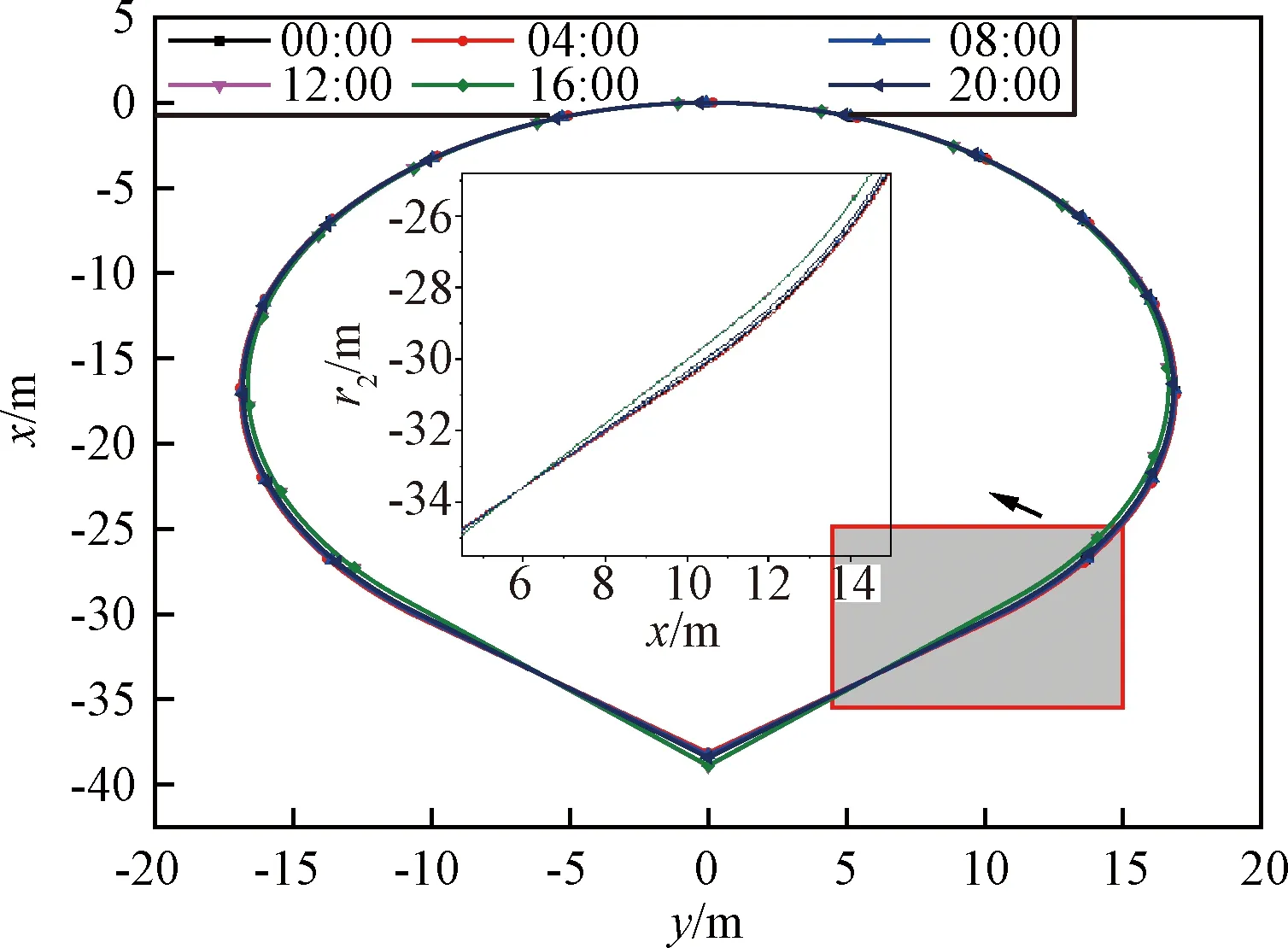
圖12 不同時刻下氣球形狀圖(20 km)Fig.12 Balloon shape at different times(20 km)

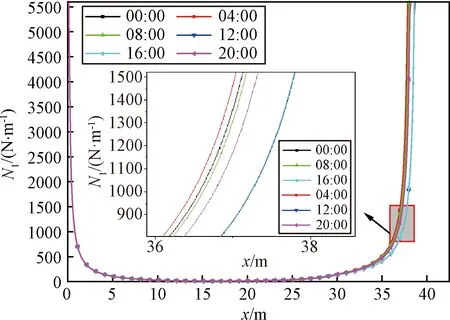
圖13 不同時刻下氣球經向應力圖(20 km)Fig.13 Balloon meridional direction stress curves atdifferent times(20 km)

3 結 論

本文建立了自然形高空氣球的熱力學模型和幾何模型，采用最小勢能法對自然形高空氣球上升過程的形狀和應力進行仿真研究，還比較了不同充氣量、不同時刻下氣球形狀及應力分布情況，得出相關結論，為氣球設計及工程應用中初步判斷氣球的形狀及應力情況提供了一種較為有效的計算方法。

1)自然形高空氣球在上升過程中由于外界環境的變化導致氣球內外壓差的變化，氣球的體積不斷變大，氣球的豎直長度逐漸減小，氣球的形狀也逐漸變成“圓球”形；氣球的經向應力不斷增大，緯向應力逐漸減小。

2)自然形氣球的經向應力分布呈“馬鞍”形，極值分布在氣球頂部和氣球底部，并且數量級較大；而緯向應力極值分布在氣球半徑最大處，數值較小，因此緯向應力對自然形高空氣球的影響較小，可以忽略。 3)不同充氣量下，在氣球的頂部和氣球的底部較大，氣球中間部分數值較小，而區別出現在氣球的底部，載荷越大，氣球底部的極值越大，氣球容易破裂；而不同時刻工況下，氣球在20 km處形狀及應力受不同時刻的影響較小。