基于電壓穩定性的配電網中電源可接入容量計算

黃宏盛，鄭 濤，彭 坤，王騰達，施文煇

（國網浙江嘉興供電公司，浙江 嘉興 314033）

0 引 言

由于電力系統電壓失穩造成的電力系統大面積的停電事故時常發生，對人們的生活以及社會經濟造成嚴重的影響[1]。針對配電網中電源可接入容量計算，保障電力系統的電壓穩定研究，對于減少事故的發生具有重要的經濟價值和社會意義。本文針對配電網中的電源可接入容量計算方法進行研究。

1 基于電壓穩定性的配電網中電源可接入容量計算

1.1 計算模型構建

在構建計算模型時，要考慮各個配電網結構與發電裝置并網的情況。電源并網的位置以及容量會影響配電網中網絡損耗的變化情況，以及造成電壓偏高等電能質量問題，影響配電網電壓的穩定。圖1為電源可接入容量計算模型圖。

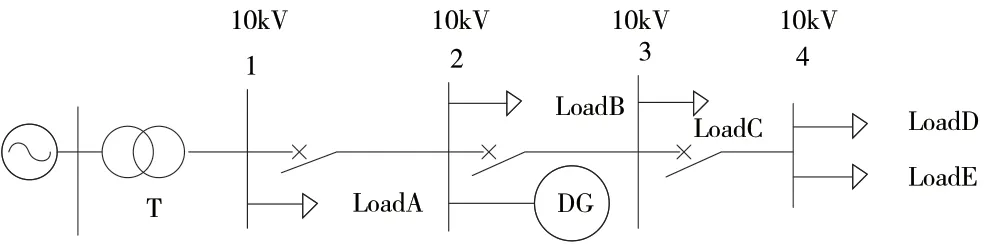
圖1 電源可接入容量計算模型圖

由于配電網中，有功功率與無功功率的變化情況都會對配電網中的電壓分布產生較大的影響[2]，因此電源接入點位置的電壓可通過如下公式進行計算：

其中，U2表示為配電網拓撲結構中節點2的電壓；U3表示為節點3位置的電壓；P表示節點2到節點3位置輸出的有功功率；Q表示為點2到節點3位置輸出的無功功率；R表示為線路2→3的電阻；X表示為線路2→3的電抗。在圖1的計算模型中，在節點1、2、3、4上均可接入電源。電源接入配電線路的首段對各節點的電壓影響較小，接入節點的位置越靠近末端，電源對于節點電壓的支撐能力越強。隨著容量的增加，接入點的電壓不斷增加，一旦超出了極限數值，會出現末端節點上的電壓遠高于前端節點上電壓的情況。

1.2 目標函數選定

在配電網中，電源輸出的無功功率和有功功率會影響整個配電網出輸出功率的大小，并且限制了輸出無功功率的積極性。假設配電網中電源以單位功率因數進行運作，即電源只輸出有功功率，則配電網中的電源可接入容量的最大值目標函數設定為：，其中N表示為接入到配電網中的電源個數；Pi表示為在某一節點i(1,2,3…)上電源輸出的有功功率。該目標函數的意義在于，配電網中的電源接入容量小于目標函數時，電力系統的運行能夠保證電壓的穩定性，當電源接入的容量超過目標函數時，電力系統將難以保證輸電網中電壓的穩定性。

1.3 約束條件設計

本文構建的數學模型需要滿足兩個約束條件，一是等式約束條件，二是不等式約束條件。等式約束條件為節點的潮流方程約束，其公式表示為：

其中，Pi表示為電源在某一節點i上注入的有功功率；Qi表示為電源在某一節點i上注入的無功功率；Ui表示為節點i的電壓幅值；Uj表示為節點j上的電壓幅值；Gij表示為電力系統導納矩陣的實部；Bij表示為電力系統導納矩陣的虛部；θij表示為節點i和節點j的電壓相角差。

電源接入到輸電網中的方式，可分為單一電源供電放射性網絡以及分布式電源供電多電源結構。在實際的配電網運行過程中，電壓需要保持在一定的合理范圍內，配電網中允許結點電壓的上限一般設置在1.06～1.08 p.u.。隨著配電網中電源不斷的接入，在配電線路上通過的電流可能會超出電壓穩定的所能承受的極限范圍，因此針對配電網中電源最大的接受能力，并考慮到輸電網電壓的穩定性，對于接入電壓的容量限制約束條件為：minUi≤Ui≤maxUi，其中minUi表示為節點i上電壓的下限；maxUi表示為節點i上電壓的上限。對于支路的容量約束條件為R1≤maxR1，其中R1表示為電源電流經過支路1時的功率；maxR1表示為支路上功率允許的最大容量，且對于支路的容量不設下限條件。

1.4 算法流程優化

對于配電網中的電源可接入容量進行計算，首先應對搜尋的方向個數進行設置，選取各個電源輸出有功功率的初始解，判斷各初始解是否滿足上文設定的約束條件，若不滿足約束條件，則直接將該初始解剔除；若滿足，則對其初始擾動以及初始步長進行設定。按照設定的方向分別進行搜尋，若能夠滿足搜尋的約束條件，則將其設定為新的基點，若不滿足則對下一個方向進行搜尋。在對各個方向進行搜尋的過程中，若所有方向都不能滿足上述約束條件，則考慮搜尋步長的設置是否合理，可將搜尋步長縮短至原來的1/2倍，再次進行搜尋。若仍無法進行搜尋，則考慮初始擾動設置是否合理，將初始擾動設置為原來的1/2倍，重復上述流程，直到找出擾動值達到滿意的精度，完成對電源可接入容量的計算。

2 實驗驗證

為了驗證本文方法的應用價值，將其與傳統的計算方法進行對比實驗。

2.1 實驗準備

構建模擬配電網電路系統，在電路中共設150個調節節點，并在末端節點與前一節點之間增加變壓器；將其變壓器分接頭調制4.5%，保證在負荷額定值與未接入電源時的配電網中節點電壓不低于0.85；為保證實驗的準確性，在配電網中不增加調壓器裝置的設置；為符合實際的配電網運行情況，在模擬配電網中，設定在隨機的幾個節點之間的開關為斷開狀態，其余為閉合狀態；實驗設定節點上的電壓上限為1.25 V，電壓下限為0.85 V。各個支路上的電源可接入容量上限設置如表1所示。

通過各個參數的設定，建立對比實驗。設傳統方法為對照組，本文方法為實驗組，在保證其他外界干擾條件及環境配電環境均相同的情況下，完成實驗對比。

2.2 實驗結果及分析

記錄兩組方法的計算結果，并隨機選取5個節點與上文設定的電源可接入容量上限進行比對，判斷兩種方法結果是否滿足上述條件，比較兩種方法計算的準確率。實驗結果如表2所示。

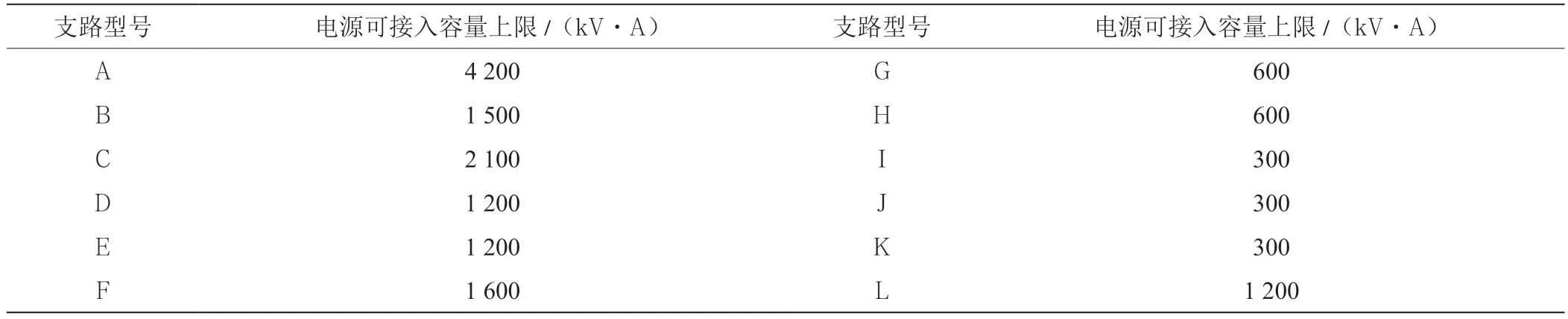
表1 電源可接入容量上限設置

表2 實驗結果對比

通過表2可以看出，實驗組計算的結果更加接近實驗前設置的數值，且實驗組的準確率明顯高于對照組。由此可以證明，本文計算方法準確率更高，能夠為配電網電源接入容量的控制提供更加準確的決策參考。

3 結 論

本文基于電壓穩定性對配電網中電源的可接入容量計算方法進行優化，考慮到電壓的水平以及支路的容量對電源接入容量的限制問題，提出了新的求解方法，并通過實驗驗證該方法的可行性和有效性，希望為未來配電網的發展和規劃提供幫助。