基于試驗和數值模擬耦合計算的汽油機缸內RGF檢測方法對比及分析

廖誠，劉敬平，任承欽，劉琦，李慶宇，付建勤

(1.湖南大學先進動力總成研究中心，湖南長沙，410082；2.湖南大學汽車車身先進設計制造國家重點實驗室，湖南長沙，410082)

在可預見的很長一段時間內，高效內燃機在交通運輸、工程機械、農業等領域將繼續發揮其難以替代的作用[1]。高效內燃機受限于特有的結構和工作過程，其發動機在工作過程中存在著“最小容積”，已燃氣體在排氣過程不可能徹底排干凈，同時，由于氣門正時和進排氣口壓力波動變化，氣道處的氣流成分和方向(正流或逆流)都發生變化，故進氣門關閉時的缸內氣體成分是一系列綜合物理過程的結果，其決定了燃燒時混合氣的成分。因此，缸內狀態參數(殘余廢氣系數、氣體成分、缸內壓力等)作為燃燒的重要初始條件，控制著整個燃燒過程，進而控制發動機經濟性、動力性和排放性等性能[2]。作為節能汽車核心部件的內燃機，必須對其進行定量化、精確化研究[3]。為了實現發動機的精準控制，必須對缸內參數進行精準而且實時檢測。參數缸內殘余廢氣系數(RGF)決定了充氣系數、混合氣稀釋度和火焰溫度以及火焰傳播速度等發動機關鍵控制參數[4-6]。人們對RGF檢測進行了大量研究，主要采用3種方法：1)直接檢測法；2)簡化預測模型；3)結合傳感器檢測的預測模型。GIANSETTI等[7-10]對直接測量法進行了研究，該方法檢測準確度較高，但需要停缸檢測，繁瑣而且耗費高，難以應用于實時檢測中。在簡化預測模型方面，KARAGIORGIS等[10-13]提出簡化預測模型，分析了影響RGF 的運行和設計參數，結合流動力學和熱力學建立簡單的預測模型，這種方法計算快，但精度有待提高。結合實測和數值仿真的方法進行RGF 檢測具有高精度和高實用性的特點，LIU 等[14-18]提出在線檢測法，其最明顯的特點是將信號實測替代數模仿真以解決時間問題，再耦合到簡化的數值模型中，使計算速度滿足實時檢測要求，既考慮了壓力波動效應與流動現象，又能比較準確地預測發動機的循環進氣量。經研究發現發動機循環進氣量的模擬計算結果與實測結果相對誤差可控制在2%以內[14]。但該方法的缺點是需要3個動態壓力傳感器和電荷放大器，價格昂貴，安裝困難，對測試系統的要求很高。基于此，本文作者提出3種簡化檢測方法：兩傳感器-動態排氣法(2PA-e 法)、兩傳感器-動態進氣法(2PA-i法)和單傳感器法(1PA法)，并連同三傳感器法(3PA 法)對1 臺增壓直噴發動機進行RGF 檢測和分析。

1 檢測方法

1.1 方法介紹

缸內RGF 檢測方法的基本思想是采用信號實測與數模仿真動態耦合求解，即基于先進傳感器測試技術，采用實測動態壓力和溫度信號與氣體動力學、熱力學過程數值仿真耦合求解的方式獲取發動機關鍵運行及性能參數。

三傳感器檢測方法(3PA 法)的示意圖及各種傳感器布置方式見圖1[19]。在發動機進、排氣道靠近氣閥處(離氣閥約100 mm)和氣缸內分別安裝1個高精度、高頻響應的瞬態壓力傳感器(時間常數為微秒級)，在進、排氣系統靠近氣閥處分別安裝1 個高頻響應的溫度傳感器(時間常數為毫秒級)，以此來測取相應位置的壓力與溫度。然后，將實測的壓力和溫度進行處理，變換為模擬計算可接受的數據形式，以此作為邊界條件實時耦合到只包含發動機氣缸和進排氣道的仿真數模中(見圖1中的陰影部分)，在此基礎上，通過自行開發的數值計算程序對發動機進排氣道內的一維非定常/非等熵流動和缸內熱力學過程進行仿真計算。

圖1 發動機瞬變過程參數檢測方案示意圖[19]Fig.1 Schematic diagram of engine transient parameter detection

對3PA 法簡化為：1) 兩傳感器-動態排氣法(2PA-e法，即將進氣高頻動態壓力傳感器p1替換為低頻穩態壓力傳感器；2) 兩傳感器-動態進氣法(2PA-i法，即將排氣高頻動態壓力傳感器p1替換為低頻穩態壓力傳感器；3)單傳感器法(1PA 法，即將進氣高頻動態壓力傳感器p1和排氣高頻動態壓力傳感器p2都替換為低頻穩態壓力傳感器)。通過簡化，可以使試驗成本大幅度降低，同時還可以提升數模計算速度，滿足實時檢測要求。

1.2 計算模型搭建

將一維氣體動力學方法(進、排氣道以及氣閥處)、0 維熱力學方法(缸內)與實測信號參數(進、排氣道管端邊界處壓力、溫度)動態耦合求解。

發動機進排氣過程可以采用一維非定常、非等熵(考慮摩擦、傳熱和管道截面變化等損失)流動方法來描述。考慮如圖2所示的控制面ABCD，若面積變化很小，且假定管內流動為一維，則相應的連續性方程、動量守恒方程和能量守恒方程可以通過如下推導得到，其中，Ff為控制體ABCD上的剪切力。

連續性方程可以表達為

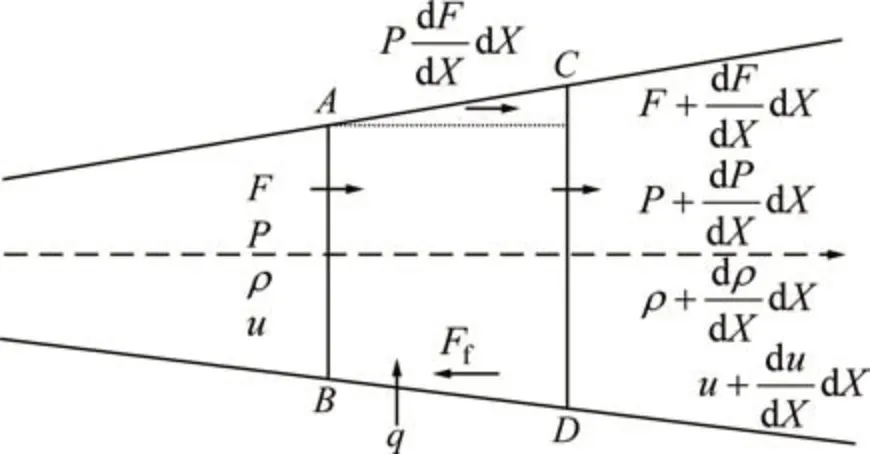
圖2 控制體示意圖Fig.2 Diagram of control body

式中：ρ為氣體密度，kg/m3；u為氣體流速，m/s；F為管道橫截面積，m2；X和t分別為長度(m)和時間(s)。

動量方程可以表達為：

式中：P為控制體內的氣體壓強，Pa；D為當量直徑，m；f為壁面摩擦因數。

能量方程可以表達為

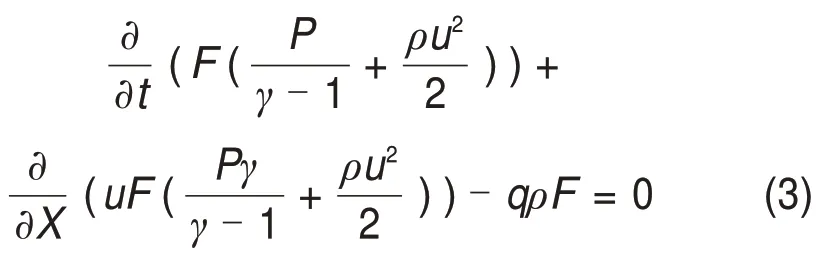
式中：γ為比熱比；q為熱流量，W。

氣體狀態方程的表達式為

式中：R為氣體常數；kJ/(kg?K)；T為氣體溫度，K。

上述流動控制方程組(偏微分方程組)無法通過解析方式求解，因此，只能采用數值求解方法求解。本文根據一種改進的、帶FCT1 技術的兩步Lax_Wendroff格式進行計算[20]。

2 試驗準備

文中涉及的汽油機的技術參數如下：發動機類型為增壓、直噴發動機；缸徑為76 mm；行程為82.6 mm；壓縮比為10；額定轉速為5 500 r/min。

對發動機進行穩態試驗工況點設置：轉速分別為2 000 和4 000 r/min，負荷p范圍為0.05 MPa至最大負荷，負荷間隔為0.10 MPa。為了描述過渡工況下缸內殘余廢氣系數(RGF)的變化情況，在發動機試驗臺上進行Load Step 試驗，即進行固定轉速下發動機怠速(或小負荷)到全負荷工況的試驗測量，試驗工況點轉速分別為1 000 r/min 和2 000 r/min。同時，為了保證實測參數精度，對主要參數測量誤差進行控制：1) 轉矩誤差在所測值的±0.05%之內；2) 轉速誤差在所測值的±0.5%以內；3)油耗量誤差在所測值的±0.12%之內；4)冷卻液流量誤差在所測值的±1%之內；5)排氣溫度誤差在所測值的±1%之內。主要測試儀器見表1。

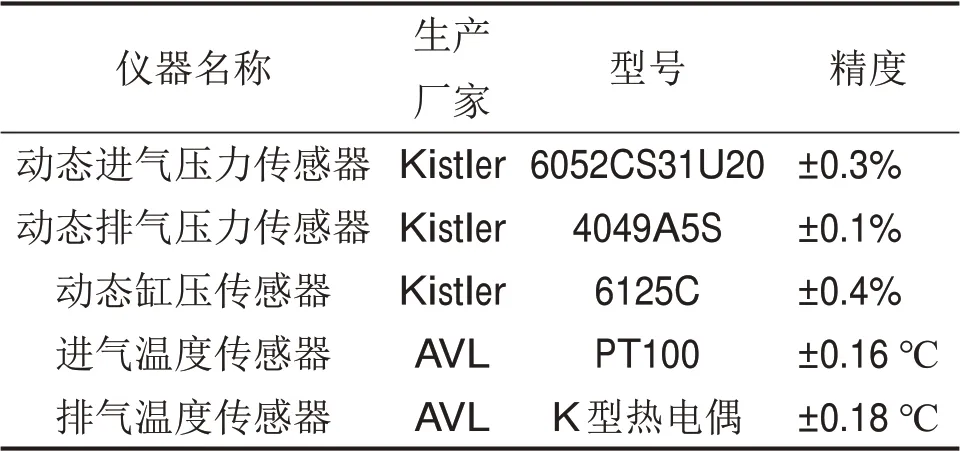
表1 主要測試儀器及精度Table 1 Main instruments and precisions

然后，通過一維氣體動力學數值式求解器直接讀取燃燒分析儀實測的瞬態缸壓、進排氣壓力傳感器實測的瞬態壓力和高頻響熱電偶輸出的溫度，在此基礎上，對包括進排氣閥在內的氣道-氣缸系統中的流動過程和熱力過程進行模擬計算。

3 結果分析

3.1 穩態結果分析

3.1.1 穩態對比

在發動機臺架上，對發動機穩態性能進行試驗，得到不同轉速和負荷下發動機的各項檢測參數，然后耦合到數值模型中，計算出不同方法下的RGF。 當轉速分別穩定在2 000 r/min 和4 000 r/min 時，3PA 法、2PA-e 法、2PA-i 法和1PA法這4 種方法所得RGF 隨平均有效壓力(p)的變化分別如圖3和圖4所示。從圖3和圖4可見：將動態壓力傳感器中的1 個(進氣或排氣壓力傳感器)或2 個(進氣和排氣壓力傳感器)替換成穩態壓力傳感器后，RGF 計算精度有一定程度降低，但整體變化趨勢一致，其中，兩傳感器-動態排氣法(2PA-e法)精度與三傳感器法(3PA法)精度接近，此兩者精度比兩傳感器-動態進氣法(2PA-i法)和單傳感器法(1PA法)的精度高。

圖3 轉速為2 000 r/min、不同負荷下缸內殘余廢氣系數(RGF)Fig.3 RGF under different loads at 2 000 r/min

圖4 轉速為4 000 r/min、不同負荷下缸內殘余廢氣系數(RGF)Fig.4 RGF under different loads at 4 000 r/min

在轉速為2 000 r/min 時(見圖3)，這4 種方法的精度在中低負荷下相差不大，當負荷p>13×105Pa時，2PA-i法和1PA法的精度大幅度下降。由圖3可以得到：1)與3PA 法相比，2PA-e 法精度最大降幅出現在p=3×105Pa 時，為4.42%，其余負荷下的精度降幅都不超過2%；2)當p<13×105Pa 時，2PA-i 法和1PA 法的精度最大降幅分別為8.24%和8.42%(當p=12×105Pa時)；當p>13×105Pa時，2PA-i法和1PA法的精度降幅超過90%。從圖4可見：在轉速為4 000 r/min 時(見圖4)，這4 種方法的精度在高負荷下相差很小，而在中低負荷下，2PA-e法、2PA-i 法和1PA 法的精度都略有下降，最大降幅分別為6.32%，6.12% 和10.30%(出現在p=10×105Pa時)。

3.1.2 差異分析

發動機RGF 受進氣壓力、進排氣壓差和氣門重疊期等運行參數的影響，進氣壓力(負荷)增大，說明進入氣缸總的工質的質量增大，RGF 隨之下降，反之亦然；進排氣壓差影響工質的流向以及流速，進而影響RGF；氣門重疊期影響倒流進氣缸或進氣管的廢氣量，從而影響RGF。

上一循環留在氣缸的廢氣質量(排氣門關閉時刻)可以表達為未排出的廢氣量加上氣門重疊期內倒流進氣管的廢氣量，表達式為

式中：mRG為殘余廢氣質量，kg；ms為排氣沖程內未排出的廢氣質量，kg；mb為氣門重疊期內倒流到進氣門的廢氣質量，kg。

選取幾個典型工況點進行分析：轉速為2 000 r/min，負荷為3×105Pa；轉速為2 000 r/min，負荷為14×105Pa；轉速為4 000 r/min，負荷為10×105Pa。分析運行參數為進氣閥處壓力、進氣流量、氣體成分比例，其中，在計算模型中，定義進氣管的135 mm 處為進氣閥處，排氣管的0 mm處為排氣閥處。氣體成分比例的定義為新鮮充質量與工質總質量的比例，當該比值為0時，說明通過某截面或留在某空間的所有工質都是廢氣；當比值為1時，說明通過某截面或留在某空間的所有工質都是新鮮空氣。

圖5 轉速為2 000 r/min、負荷為3×105Pa時進氣閥處參數隨曲軸轉角變化關系Fig.5 Parameters change with crank angle through the inlet valve at 2 000 r/min and 3×105Pa

當轉速為2 000 r/min、負荷為3×105Pa 時，進、排氣閥處參數隨曲軸轉角變化關系分別如圖5和圖6所示。從圖5(a)可見：將動態傳感器替換成穩態傳感器，影響的是計算模型的壓力邊界條件，由于都采用動態進氣壓力傳感器，故2PA-i法進氣壓力和3PA法進氣壓力在進氣開始前基本保持相同且呈現波動狀態，而2PA-e法和1PA法的進氣壓力則基本平穩；進氣門開啟后，剛開始進氣時，由于這4種方法的進氣閥處壓力基本相同，故倒流進進氣道的廢氣量也基本相同，見圖5(b)中標示處；在進氣過程后期，雖然這4 種方法的壓力呈現差異，但此過程流入流出氣缸的工質都是新鮮空氣(結合圖5(c))，故留在氣缸的廢氣量不再變化。從圖6可見：由于都采用動態排氣壓力傳感器，2PAe法排氣壓力和3PA法排氣壓力基本保持一致，且在4種方法下，流過排氣閥的流量差異不大，故排氣過程計算對不同方法的精度影響不大。根據以上分析可知，這4種方法的進氣和排氣過程沒有產生明顯差異，故用這4 種方法計算的此工況點的RGF相差不大。

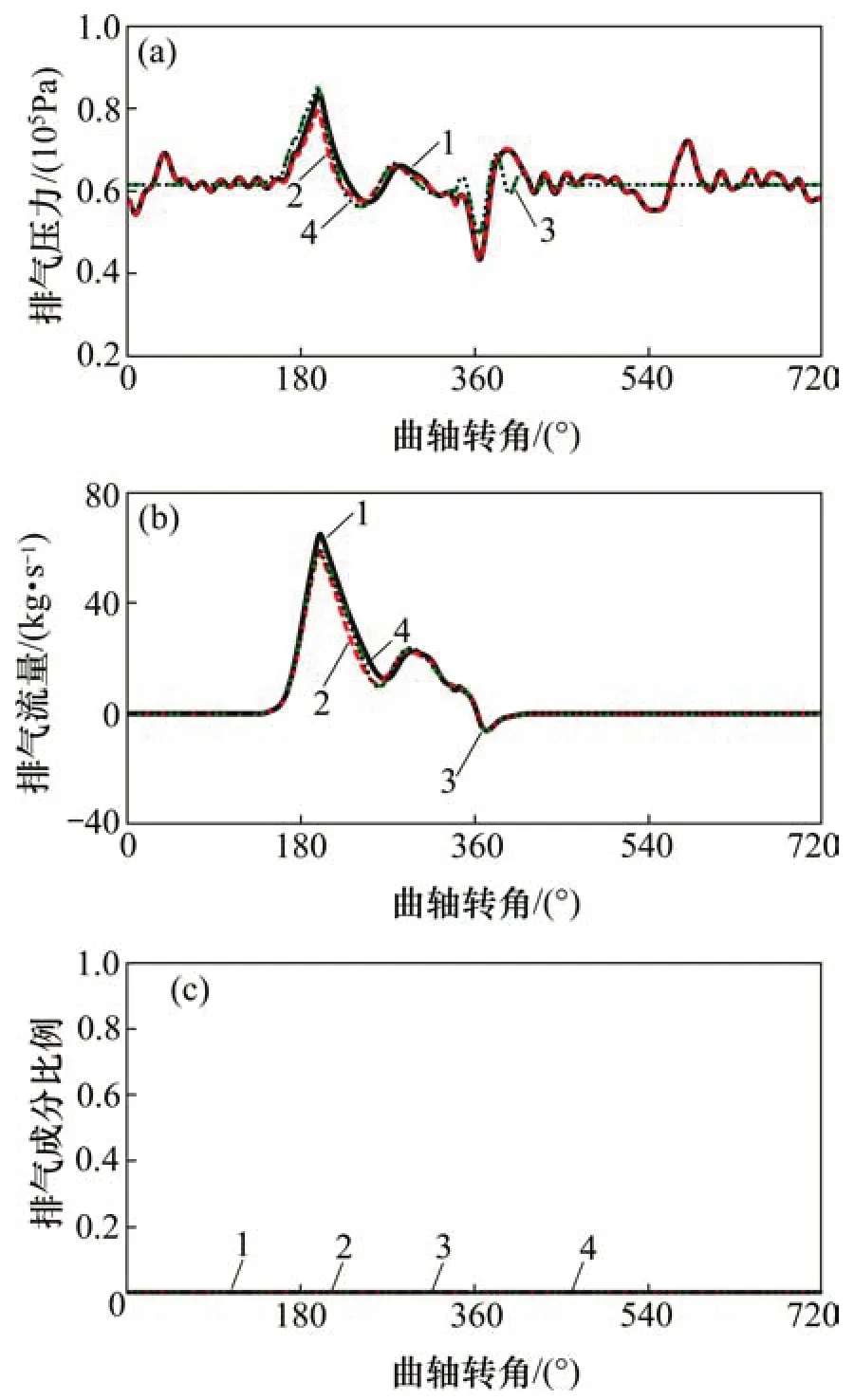
圖6 轉速為2 000 r/min、負荷為3×105Pa時排氣閥處參數隨曲軸轉角變化Fig.6 Parameters change with crank angle through outlet valve at 2 000 r/min and 3×105Pa

當轉速為2 000 r/min、負荷為14×105Pa 時，進、排氣閥處參數隨曲軸轉角變化關系分別如圖7和圖8所示。從圖7和圖8可見：當負荷增大時，進排氣壓力波的波動幅值大大增加，排氣壓力的范圍為1.2×105～3×105Pa，而在低負荷時，排氣壓力范圍僅僅為0.8×105～1.2×105Pa。由于這4種方法都是采用相同的缸壓傳感器測量，根據上面分析，排氣沖程內未排出的廢氣量(留在氣缸內的廢氣量)相差不大，故這里主要分析進氣開始時倒流入進氣管的廢氣量。結合圖7和圖8可以得到：因為檢測方法存在差異，在氣門重疊期內，以穩態排氣壓力傳感器測試的數據傳導到排氣閥處的壓力波沒有產生較大的變化幅度，而這與排氣閥處急劇變化的壓力波真實值相差較大，這便是產生精度差異的主要原因。通過影響進排氣壓差，使得2PA-i法、1PA法與2PA-e法、3PA法倒流進進氣管的廢氣量相比大大增加，即RGF 大幅度提升，使得此工況點計算的數據失真嚴重。

當轉速為4 000 r/min、負荷為10×105Pa 時，進、排氣閥處參數隨曲軸轉角的變化分別如圖9和圖10所示。從圖9和圖10可見：由于高轉速下進排氣壓力波的波動頻率增大，即使測量點換成平穩的壓力，經過幾次來回傳導，在氣閥處的壓力也將呈現疊加放大效應，因此，穩態壓力傳感器與動態壓力傳感器相比，其壓力邊界數據傳導的誤差沒有低轉速時的大。

圖7 轉速為2 000 r/min、負荷為14×105Pa時進氣閥處參數隨曲軸轉角變化Fig.7 Parameters change with crank angle through inlet valve at 2 000 r/min and 14×105Pa

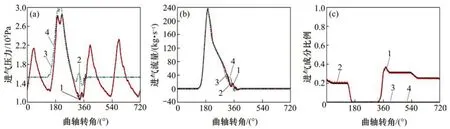
圖8 轉速為2 000 r/min、負荷為14×105Pa時排氣閥處參數隨曲軸轉角變化Fig.8 Parameters change with crank angle through outlet valve at 2 000 r/min and 14×105Pa

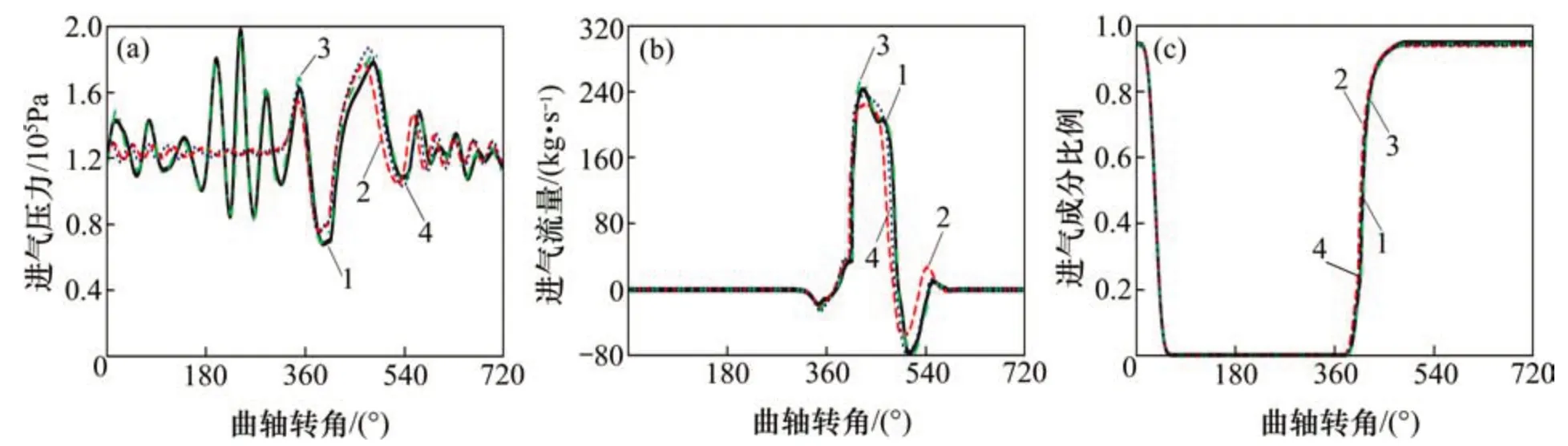
圖9 轉速為4 000 r/min、負荷為10×105Pa時進氣閥處各個參數隨曲軸轉角變化Fig.9 Parameters change with crank angle through inlet valve at 4 000 r/min and 10×105Pa

圖10 轉速為4 000 r/min、負荷為10×105Pa時排氣閥處各個參數隨曲軸轉角變化Fig.10 Parameters change with crank angle through outlet valve at 4 000 r/min and 10×105Pa

3.2 瞬態結果分析

在發動機臺架上，將發動機轉速分別穩定在1 000 r/min 和2 000 r/min，進行過渡工況模擬(Load Step試驗，從高負荷到低負荷)，并根據上述檢測方法，計算每個循環的RGF，如圖11和圖12所示。從圖11和圖12可見：在過渡工況下，由于進排氣壓力波沒有穩定，2PA-e法、2PA-i法和IPA法這3 種方法計算的RGF 與三傳感器法(3PA)相比呈現一定的波動性；在過渡工況下，這3種方法在過渡循環工況中的RGF 趨勢一致性吻合較好，特別是2PA-e 法，精度與3PA 的基本吻合，并且比2PA-i法和1PA法的高。

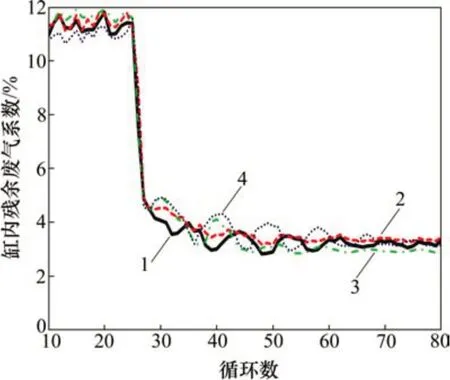
圖11 轉速為1 000 r/min、過渡工況下缸內殘余廢氣系數(RGF)隨循環數的變化Fig.11 RGF changes with cycle number in transition condition at 1 000 r/min

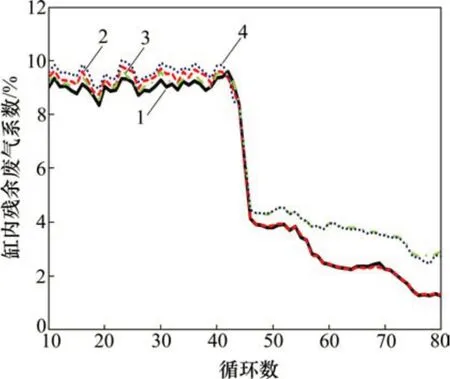
圖12 轉速為2 000 r/min、過渡工況下缸內殘余廢氣系數(RGF)隨循環數的變化Fig.12 RGF changes with cycle number in transition condition at 2 000 r/min

4 結論

1)在三傳感器法(3PA法)的基礎上，提出簡化的檢測方法，即兩傳感器-動態排氣法(2PA-e 法)、兩傳感器-動態進氣法(2PA-i法)和單傳感器法(1PA法)，并分別采用4種方法對1臺增壓直噴發動機缸內殘余廢氣系數(RGF)進行檢測試驗。結果表明，所提出的這3種方法與3PA法相比計算精算都有所下降，但變化趨勢一致，2PA-e法與3PA法精度接近，比2PA-i法和1PA法的高。

2) 在 轉 速 為2 000 r/min 時，2PA-e 法、2PA-i法、1PA法和3PA法這4種方法的精度在中低負荷下相差不大，當負荷p>13×105Pa 時，2PA-i 法和1PA 法的精度大幅度下降，2PA-e 法和3PA 法檢測的精度相比較最大降幅為4.42%；在轉速為4 000 r/min時，這4種方法的精度在高負荷下基本吻合，在全負荷下相差不大，2PA-e法和3PA法檢測的精度相比較，最大降幅6.32%。

3)這4種檢測方法的精度差異主要體現在是否有壓力波的影響上，進而影響氣閥處的壓力，使得進排氣壓差出現誤差，最后影響進氣開始時倒流入進氣管的廢氣量，導致計算缸內殘余廢氣系數(RGF)存在差異，即氣門重疊期倒流入進氣管的廢氣量差異是導致RGF計算差異的主要因素。

4)在過渡工況下，由于進排氣壓力波沒有穩定，2PA-e法、2PA-i法和1PA法這3種方法計算的RGF與3PA法相比呈現一定的波動性，這3種方法在過渡循環工況中趨勢一致性好，特別是2PA-e法，其精度與3PA 法的精度基本吻合，且比2PA-i法和1PA法的精度高。