基于非局部均值去噪和快速譜相關(guān)的滾動軸承早期故障診斷方法

萬書亭，彭勃

(華北電力大學機械工程系，河北保定，071003)

滾動軸承作為旋轉(zhuǎn)機械的重要“關(guān)節(jié)”，是機械系統(tǒng)的重要零部件之一，當其出現(xiàn)故障時會影響到整個設備的安全運行[1-4]。滾動軸承早期故障時，傳感器采集到的振動信號沖擊分量較弱，經(jīng)常被強背景噪聲淹沒，給診斷過程帶來了難度。滾動軸承早期故障診斷一直是研究人員和學者們關(guān)注的焦點和難點。小波變換[5]、盲源分離[6]和經(jīng)驗模態(tài)分解[7]等分解重構(gòu)方法雖然能夠有效地分離噪聲和原始信號，但也會導致信號局部信息失真和細節(jié)丟失。BUADES等[8]利用信號的自相似性提出了用于圖像去噪的非局部均值(NLM)算法。TRACEY 等[9]和胡新海等[10]應用NLM 算法分別處理ECG 信號和地震信號，去噪后的信號均具有較大的信噪比。Lü等[11]在經(jīng)典NLM算法的基礎上提出了一維NLM 快速算法，并與包絡譜分析法相結(jié)合，成功提取出滾動軸承故障特征。VAN 等[12]將NLM，EMD 和包絡檢測相結(jié)合，利用NLM 算法首先對原始信號進行去噪處理降低背景噪聲，然后利用EMD 將去噪信號分解為有限個本征模態(tài)分量(IMF)，最后對第一個IMF 分量進行包絡譜分析，提取滾動軸承故障特征。熊國良等[13]將NLM和譜峭度(SK)相結(jié)合，首先利用SK算法對原始信號進行分析，并據(jù)此構(gòu)造出帶通濾波器實現(xiàn)初步降噪，然后應用NLM 算法進一步去除帶內(nèi)噪聲，最后從濾波信號的包絡譜中提取故障特征頻率。滾動軸承表面局部缺陷產(chǎn)生的周期性沖擊使其振動信號具有循環(huán)平穩(wěn)特征，將循環(huán)平穩(wěn)理論應用于軸承故障診斷領域[14-16]。譜相關(guān)分析方法是最有效的基于循環(huán)平穩(wěn)理論的方法之一。與經(jīng)典的譜分析方法不同，譜相關(guān)可以增強分析信號中蘊含的周期性成分。平均周期圖(ACP)是軸承故障檢測中廣泛使用的譜相關(guān)估計方法[17]。周徐寧等[18]將ACP 與隱馬爾可夫模型相結(jié)合實現(xiàn)了滾動軸承故障診斷。ANTONI等[19-20]對有關(guān)軸承信號的譜相關(guān)技術(shù)進行了研究，針對傳統(tǒng)譜相關(guān)技術(shù)計算效率較低的問題提出了快速譜相關(guān)(FSC)方法。針對如何抑制滾動軸承早期故障振動信號中噪聲和諧波干擾，增強并提取微弱故障特征，本文作者首先利用NLM 算法處理原始振動信號，降低背景噪聲。然后，對降噪信號進行快速譜相關(guān)分析，增強信號中的周期成分，獲得快速譜相關(guān)譜及其對應的增強包絡譜。最后，識別增強包絡譜中幅值突出的頻率成分，準確判斷故障類型。通過對仿真故障信號、實驗故障信號進行分析，驗證了本文提出方法的有效性。

1 理論背景

1.1 非局部均值去噪

自然圖像中存在大量的類似成分，基于加權(quán)平均法搜尋類似成分去除隨機噪聲的NLM 算法被提出[11]。因NLM 算法可以有效保留信號中的細節(jié)信息和尖銳邊緣，被用于解決一維信號處理問題。假設1個一維信號x(t)被1個高斯白噪聲信號n(t)污染，則含噪聲信號為

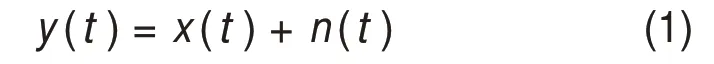
NLM算法是通過計算y(t)中全部相似塊的加權(quán)平均(t)對原始x(t)進行估計進而實現(xiàn)去噪。(t)的計算過程如下：

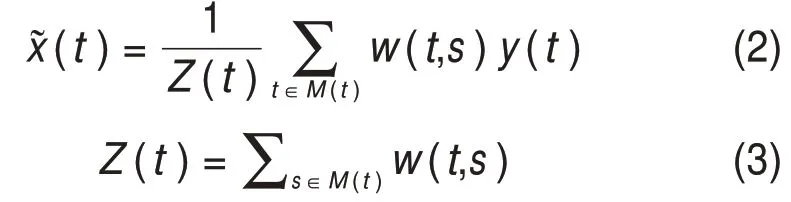
式中：w(s,t)為以t和s為中心的2 個搜索塊之間的相似度；t為以點t為中心的搜索塊；M(t)為搜索域中全部點的集合；Z(t)為歸一化常數(shù)，表示全部搜索塊相似度之和。w(s,t)需要滿足如下2個條件：

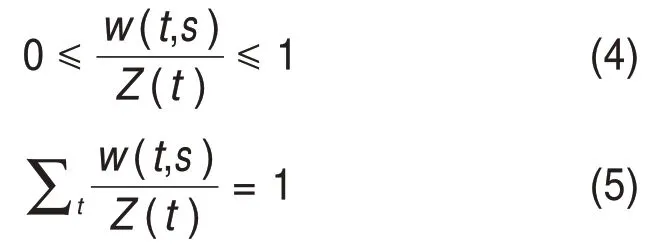
w(s,t)的計算過程如下：

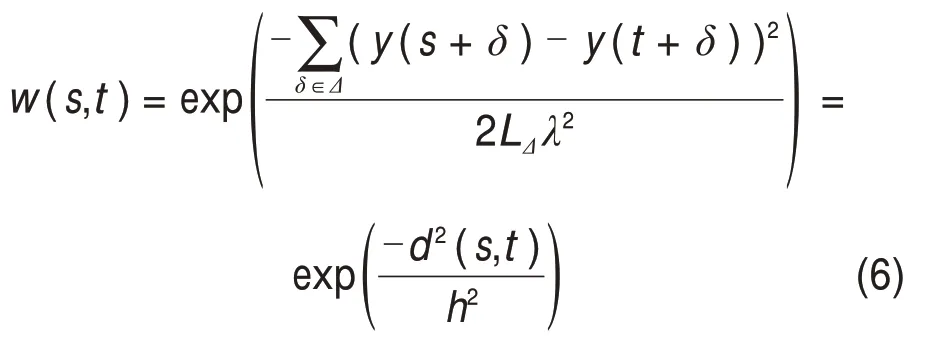
式中：λ為濾波器帶寬參數(shù)；Δ為以t為中心的搜索塊；LΔ為以s為中心的搜索塊；d2(s,t)為以t和s為中心的2個搜索塊之間歐氏距離的平方和，其數(shù)值越小，表示相似度越大；d2決定w(s,t)的衰減速度，進而控制濾波器的性能。

1.2 快速譜相關(guān)

FSC算法是由ANTONI等[20]提出的，其可以降低計算譜相關(guān)的時間且不影響效率。假設x(tn)是一個循環(huán)平穩(wěn)信號，其譜相關(guān)性定義為

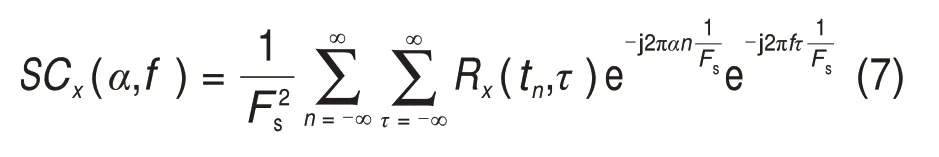
式中：Fs為采樣頻率；tn為時間瞬間，tn=n/Fs；Rx(tn,τ)為x(tn)的循環(huán)自相關(guān)函數(shù)；τ為時間延遲；α為循環(huán)頻率；f為信號頻率。譜相關(guān)是2 個頻率變量的二維傅里葉變換，反映了信號相對于頻率和循環(huán)頻率的功率分布。

為了提高計算譜相關(guān)效率，引入短時傅里葉變換。信號x(tn)的短時傅里葉變換(STFT)分析過程如下：

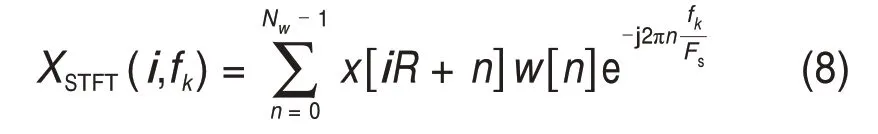
式中：Nw為STFT的窗長；R為STFT 中的塊移位；w(n)為窗函數(shù)；x[n]為x(tn)的縮寫形式；fk為離散頻率，fk=kΔf，k=1,2,…,Nw-1；Δf為頻率分辨率，Δf=Fs/Nw。

STFT的相位校正過程如下：

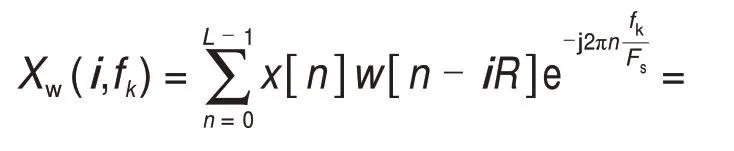
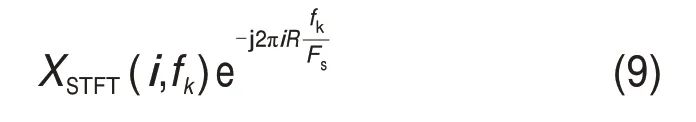
式中：Xw(i,fk)為信號x(tn)在iR/Fs處的復包絡；|Xw(i,fk)|2為頻帶的能量流。

基于STFT的循環(huán)譜計算過程為

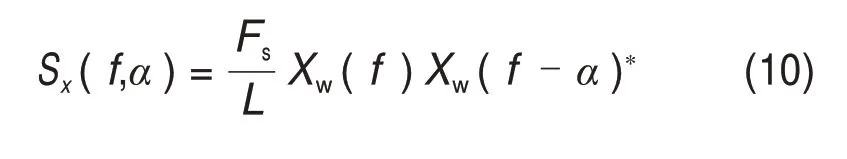
式中：L為信號x(tn)的長度。

假設f=fk=kΔf和α=pΔf+δ，可以推斷f-α=fk-α≈fk-p和α≈pΔf。基于此，式(3)可以寫為

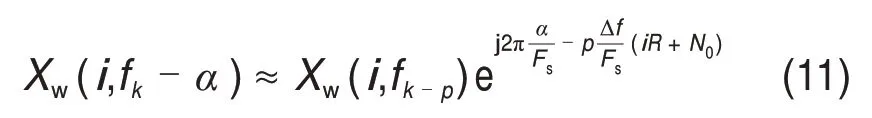
式中：p為最接近給定循環(huán)頻率α的STFT 頻率指數(shù)；δ為余數(shù)。

將式(11)和式(9)代入式(10)，得：

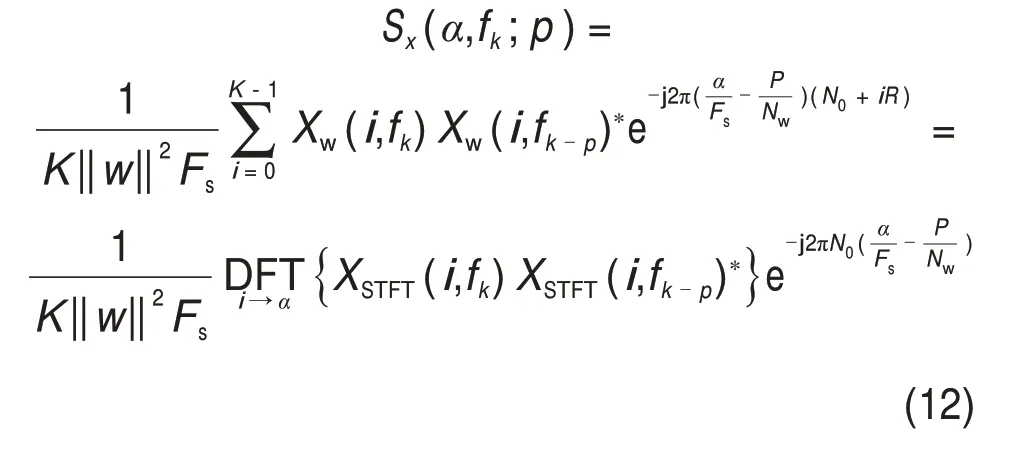
式中：DFT表示離散傅里葉變換。

當p=0 時，信號x(tn)的周期為T，其循環(huán)頻率α=1/T，能量在頻帶[fk-Δf/2,fk+Δf/2]內(nèi)周期性流動；當p≠0 時，Xw(i,fk)Xw(i,fk-p)*表示能量在頻帶[fk-Δf/2,fk+Δf/2]與頻帶[fk-p-Δf/2,fk-p+Δf/2]之間流動。

快速譜相關(guān)的定義為：

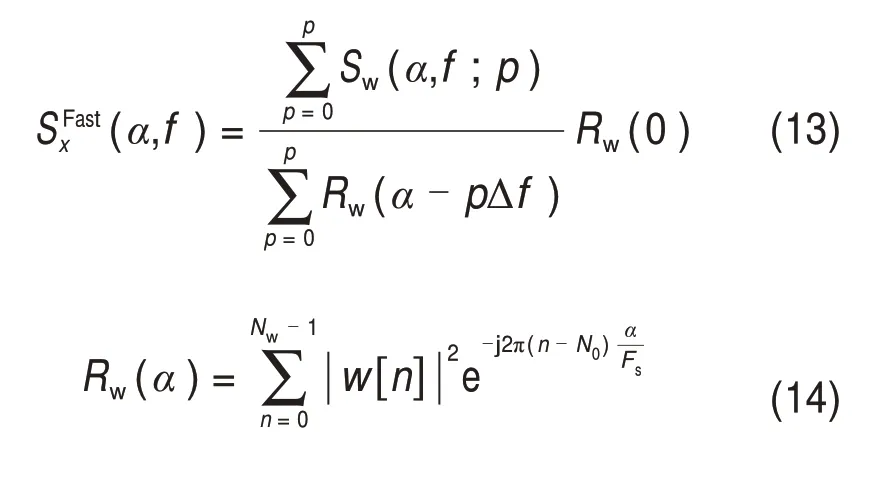
式中：Rw(α)為核函數(shù)；Rx(0)=||w||2。

快速譜相關(guān)函數(shù)定義為

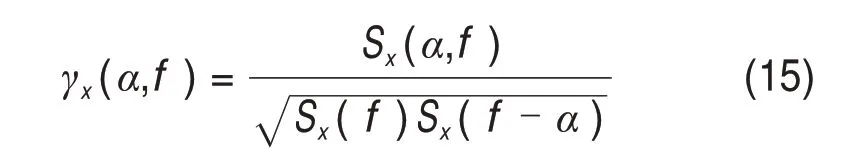
增強包絡譜定義為

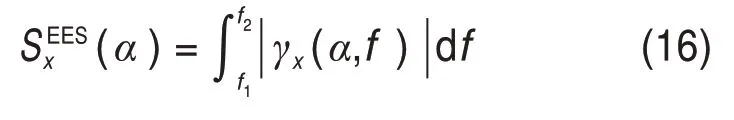
2 基于NLM-FSC 的滾動軸承早期故障診斷

NLM 算法具有良好的提高信號信噪比性能，F(xiàn)SC算法具有增強信號中周期成分的特性，本文提出了基于NLM-FSC 的滾動軸承早期故障診斷方法，診斷過程如圖1所示。

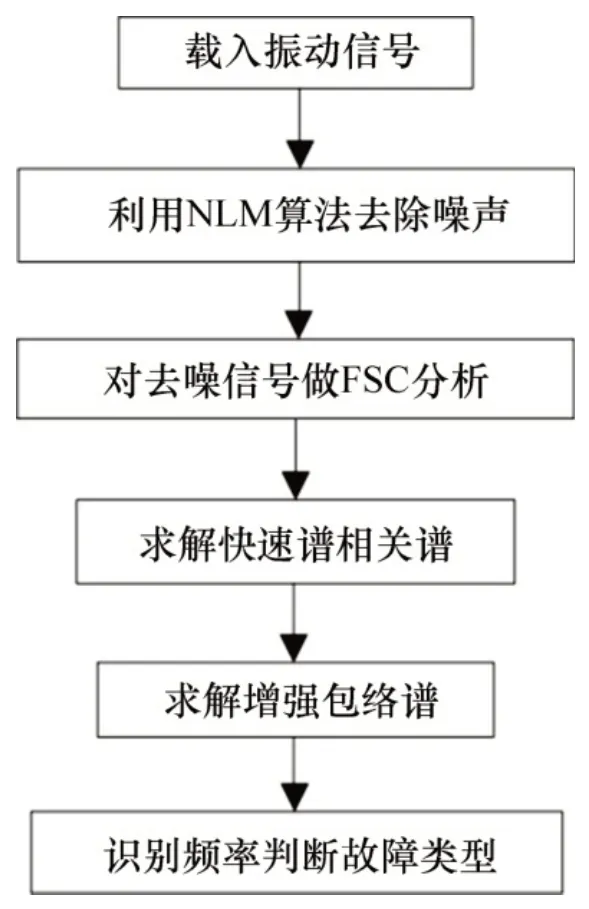
圖1 NLM-FSC方法診斷流程圖Fig.1 Diagnostic flow chart of NLM-FSC method

3 仿真信號分析

采用滾動軸承故障模型[21]疊加高斯白噪聲的方式來仿真內(nèi)圈早期故障，數(shù)學模型如下：

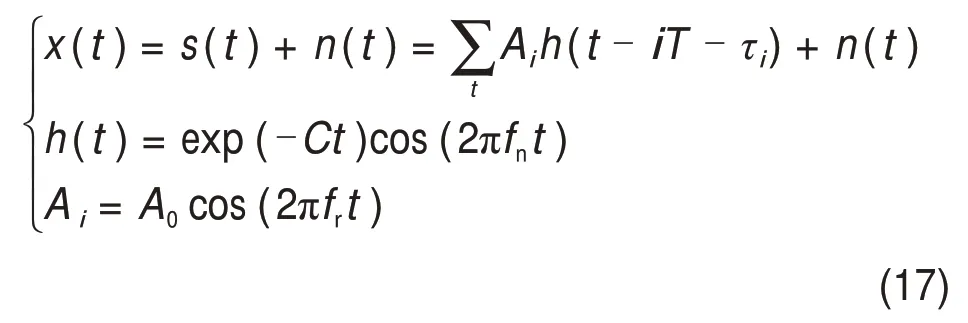
式中：s(t)為內(nèi)圈缺陷產(chǎn)生的周期性沖擊分量；n(t)為高斯白噪聲；A0為信號振幅；fn為系統(tǒng)共振頻率；fr為軸轉(zhuǎn)動頻率；τi為第i次沖擊相對于沖擊周期T的波動，且服從μ=0，σ2=0.5%×fr的正態(tài)分布；fi為內(nèi)圈故障特征頻率，且fi=1/T；C為系統(tǒng)衰減系數(shù)。仿真信號所需參數(shù)如表1所示。表1中Fs為信號的采樣頻率；N為信號為采樣點數(shù)。仿真信號的信噪比(SNR)為-12 dB。

表1 內(nèi)圈故障仿真信號參數(shù)Table 1 Parameter of inner race fault simulation signal

圖2(a)所示為滾動軸承內(nèi)圈早期故障仿真信號的時域波形。從圖2(a)可見；周期性沖擊分量被強噪聲掩蓋，不能觀察到故障信息。對仿真信號進行包絡解調(diào)，圖2(b)所示為仿真信號的包絡譜。從圖2(b)可見有3 倍的內(nèi)圈故障頻率(3fi)的諧波出現(xiàn)。

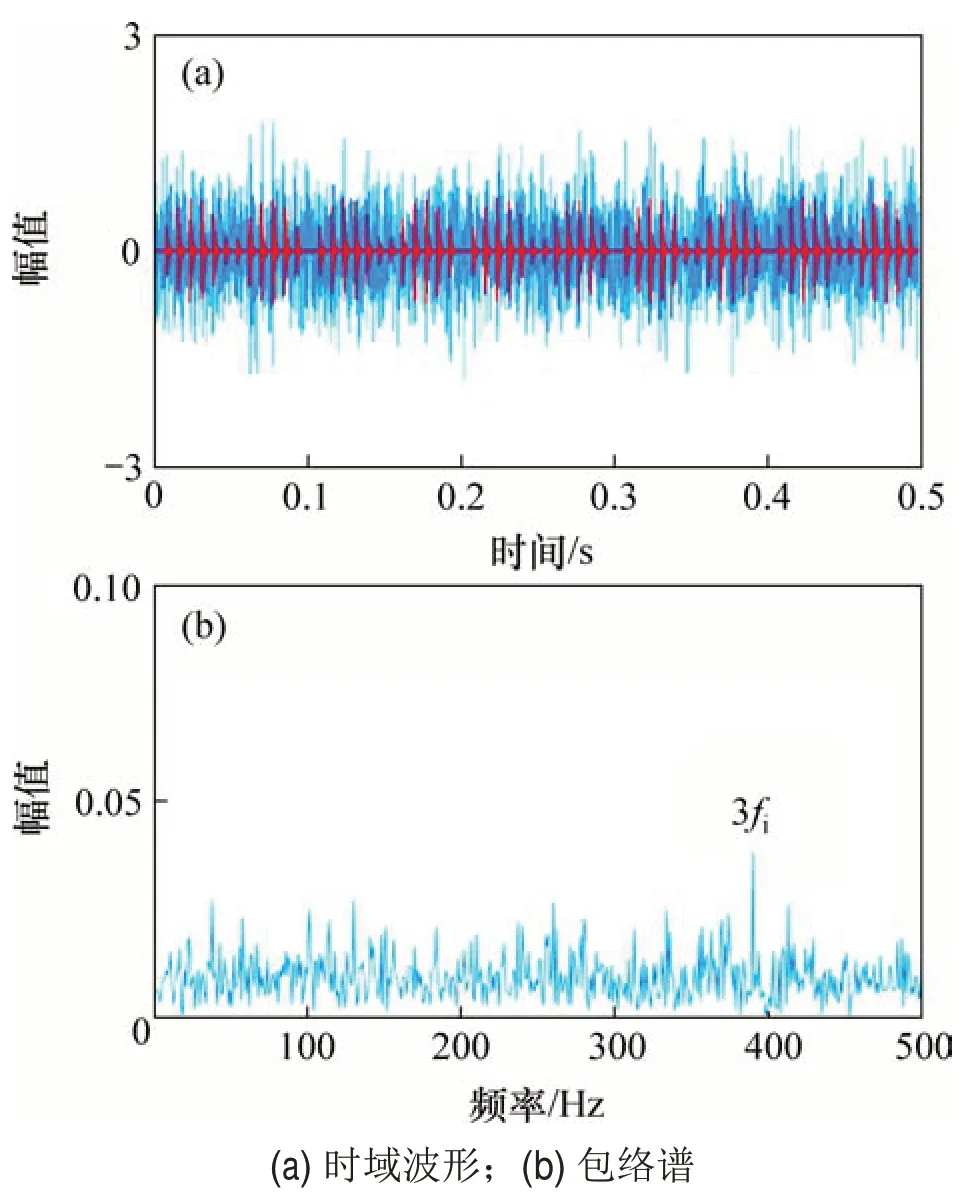
圖2 仿真信號時域波形及其包絡譜Fig.2 Time domain waveform and envelope spectrum of simulation signal

使用本文方法對仿真信號進行分析。首先，對故障信號進行NLM去噪，去噪后信號時域波形如圖3(a)所示。然后，對去噪后信號進行快速譜相關(guān)分析，圖3(b)所示為去噪信號的快速譜相關(guān)譜，在故障特征頻率處出現(xiàn)明顯的能量集中。圖3(c)所示為相關(guān)譜對應的增強包絡譜，有明顯的內(nèi)圈故障頻率(fi)及其2 倍頻(2fi)和3 倍頻(3fi)的諧波出現(xiàn)，且噪聲頻率被明顯抑制。利用本文方法可以有效地提取信號的故障特征頻率，準確判斷故障為內(nèi)圈故障。

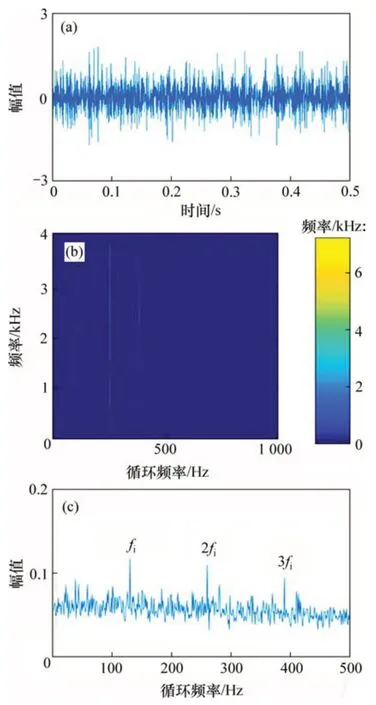
圖3 本文提出方法的分析結(jié)果Fig.3 Analysis results of proposed method

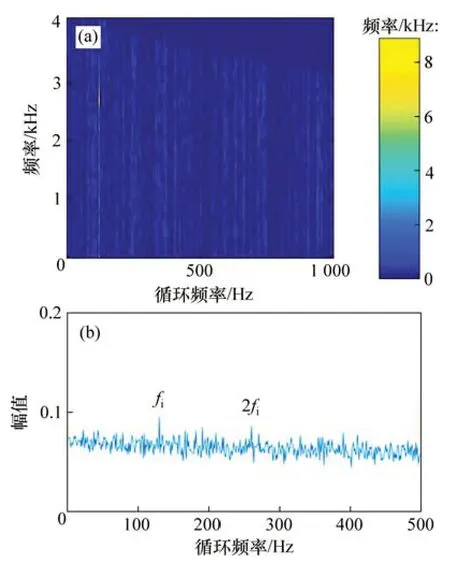
圖4 快速譜相關(guān)方法的分析結(jié)果Fig.4 Analysis results of FSC method

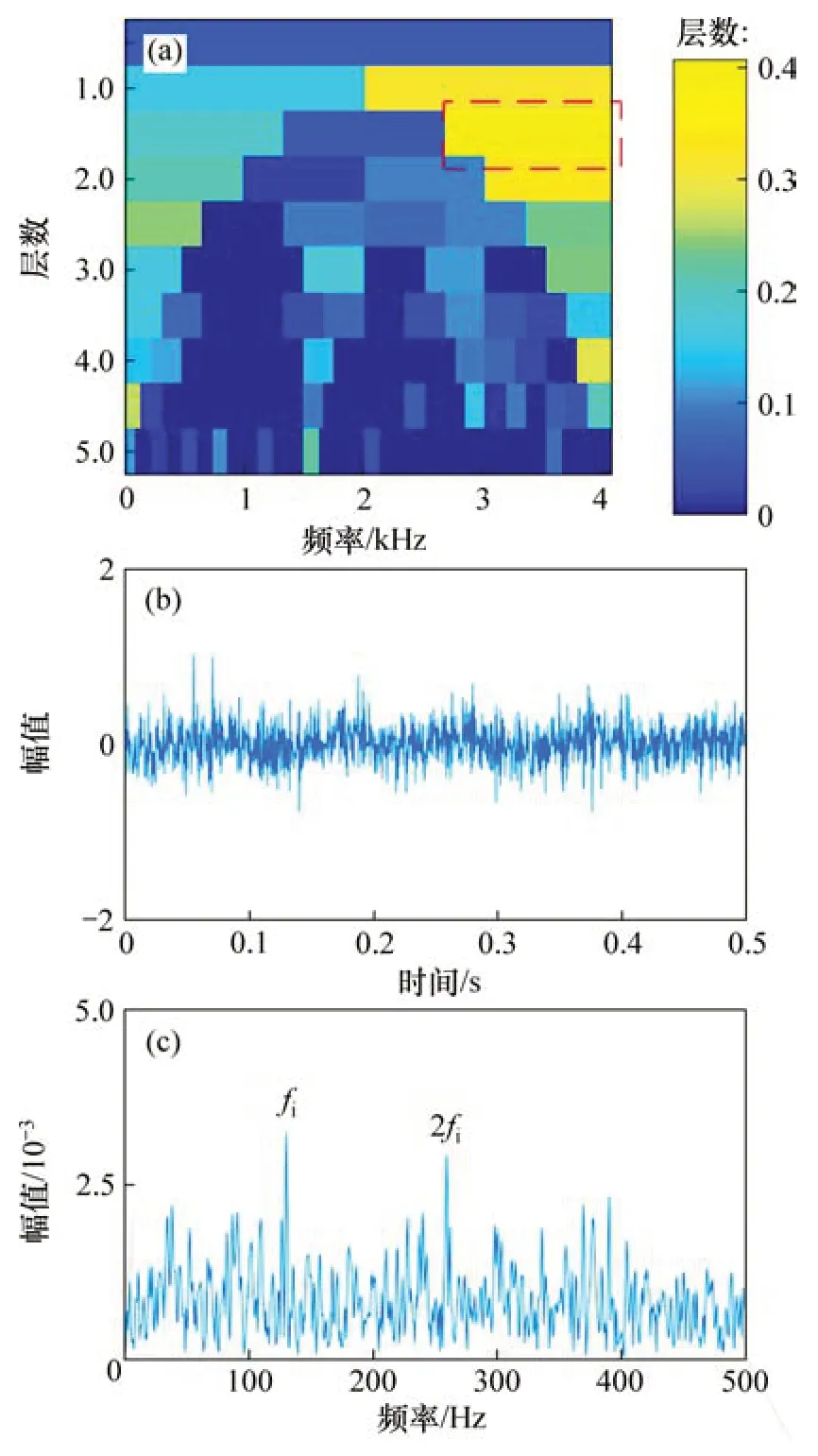
圖5 SK-NLM方法的分析結(jié)果Fig.5 Analysis results of SK-NLM method

為了驗證本文方法的優(yōu)越性，使用快速譜相關(guān)方法，譜峭度結(jié)合非局部均值去噪方法(SKNLM)以及非局部均值去噪結(jié)合經(jīng)驗模態(tài)分解方法(NLM-EMD)分別對內(nèi)圈故障仿真信號進行分析。圖4(a)和圖4(b)所示分別為仿真信號的快速譜相關(guān)譜及其對應的增強包絡譜。從圖4可見：內(nèi)圈故障頻率(fi)及其2 倍頻(2fi)諧波出現(xiàn)，但特征頻率幅值與噪聲頻率相比并不突出。根據(jù)文獻[12]中的診斷過程，首先對仿真信號進行譜峭度分析，圖5(a)所示為對應的峭度圖。根據(jù)最大峭度(圖5(a)中被虛線圈出)構(gòu)造出中心頻率為3 412 Hz、帶寬為1 365 Hz的帶通濾波器對仿真信號進行一次去噪。然后，利用NLM方法對信號進行二次降噪。圖5(b)和圖5(c)所示分別為二次去噪信號的時域波形和包絡譜。從圖5(b)和5(c)可見：內(nèi)圈故障頻率(fi)及其2 倍頻(2fi)諧波出現(xiàn)，但噪聲頻率沒有明顯被抑制。根據(jù)文獻[13]中的診斷過程，首先利用NLM 方法對信號進行降噪處理，結(jié)果如圖6(a)所示。然后，利用EMD 算法分解降噪后信號得到一系列IMF 分量，選擇IMF 1 分量進行包絡解調(diào)分析。圖6(b)和圖6(c)所示分別為IMF 1分量的時域波形和包絡譜。包絡譜中有2 倍和3 倍的內(nèi)圈故障頻率(2fi和3fi)的諧波出現(xiàn)，但諧波幅值與噪聲頻率幅值接近，容易被誤診為噪聲。上述分析結(jié)果表明：相較于FSC方法、SK-NLM 方法以及NLM-EMD 方法，本文方法可以抑制噪聲干擾，有效提取故障特征，準確診斷故障類型。

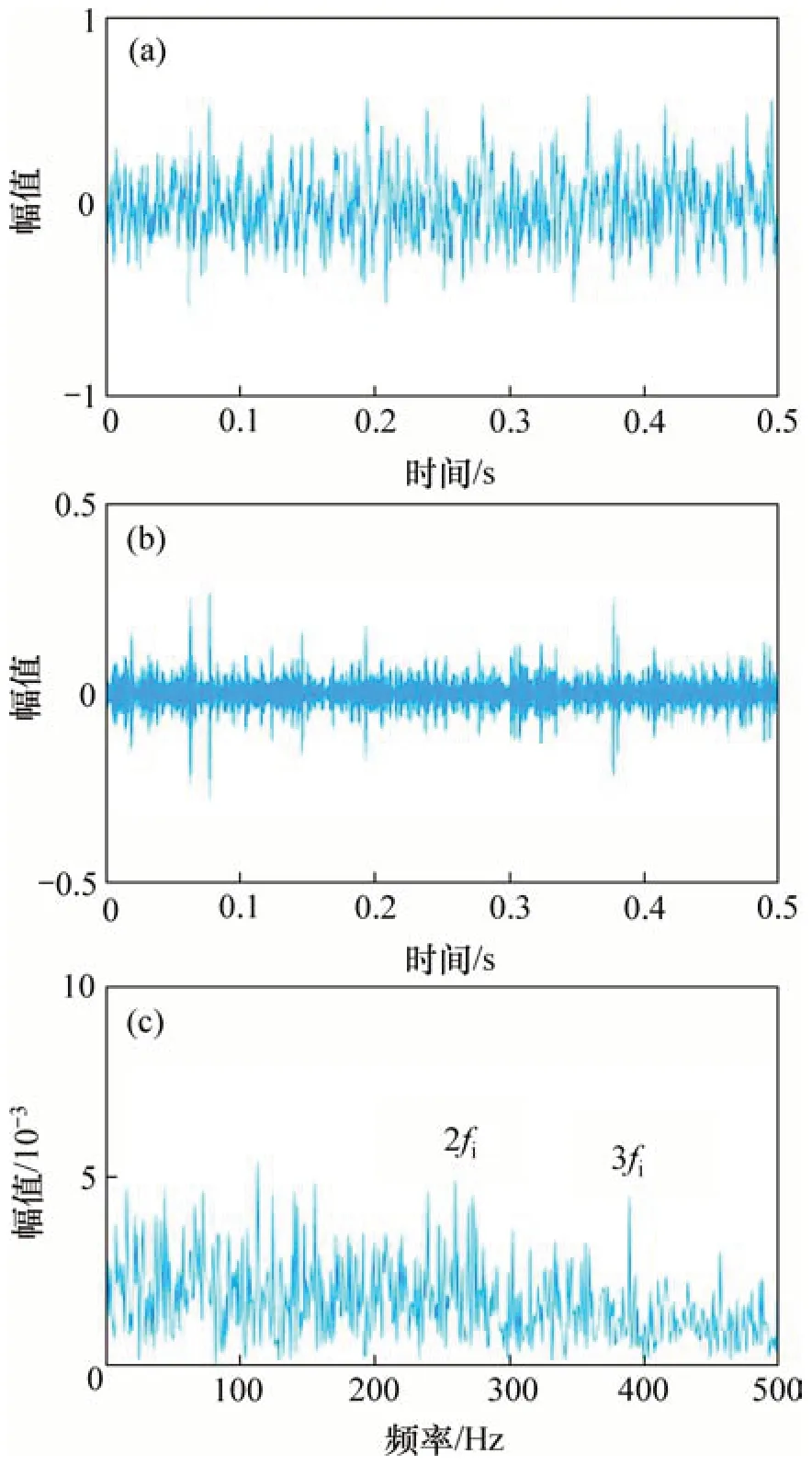
圖6 NLM-EMD方法的分析結(jié)果Fig.6 Analysis results of NLM-EMD method

4 實驗信號分析

為進一步說明本文方法在實際應用中的可行性，在QPZZ-II 型旋轉(zhuǎn)機械故障試驗臺上開展了滾動軸承外圈微弱故障實驗[22]。圖7所示為實驗臺的整體外觀。從圖7可見：旋轉(zhuǎn)軸通過聯(lián)軸器和皮帶輪與驅(qū)動電機連接。壓力加載裝置和轉(zhuǎn)子盤固定在旋轉(zhuǎn)軸上。正常軸承固定在左側(cè)軸承座上，故障軸承固定在右側(cè)軸承座上。實驗對象為SKF 6203型滾動軸承，其結(jié)構(gòu)參數(shù)如表2所示。采用線切割技術(shù)在外環(huán)上加工出寬度為0.1 mm、深度為0.2 mm 的凹槽，模擬滾動軸承的外圈微弱故障，如圖8所示。傳感器固定在右軸承座上，采集振動信號。實驗時，驅(qū)動電機轉(zhuǎn)頻fr為24 Hz，采樣頻率fs為12.8 kHz。將表2所示參數(shù)和軸轉(zhuǎn)頻代入式(18)，計算得到外圈故障特征頻率fo≈88 Hz。

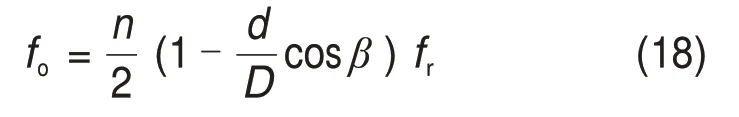
式中：n為滾動體個數(shù)；d為滾動體直徑；D為節(jié)圓直徑；β為接觸角。

圖7 QPZZ-II型實驗平臺Fig.7 QPZZ-II experiment platform

表2 SKF 6203型軸承結(jié)構(gòu)參數(shù)Table 2 Bearing structure parameter of SKF 6203

圖8 軸承外圈故障Fig.8 Bearing outer race fault

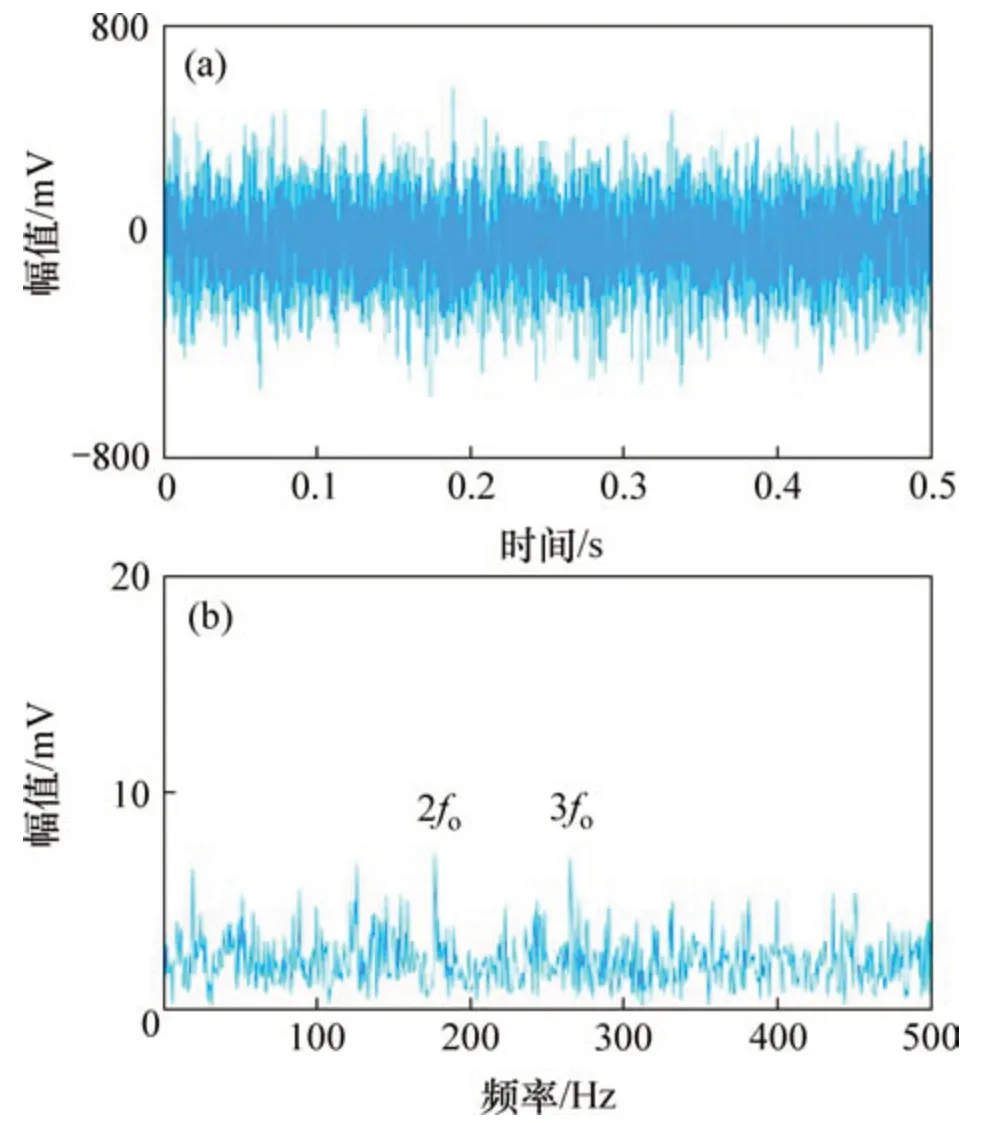
圖9 實驗信號時域波形及其包絡譜Fig.9 Time domain waveform and envelope spectrum of experiment signal

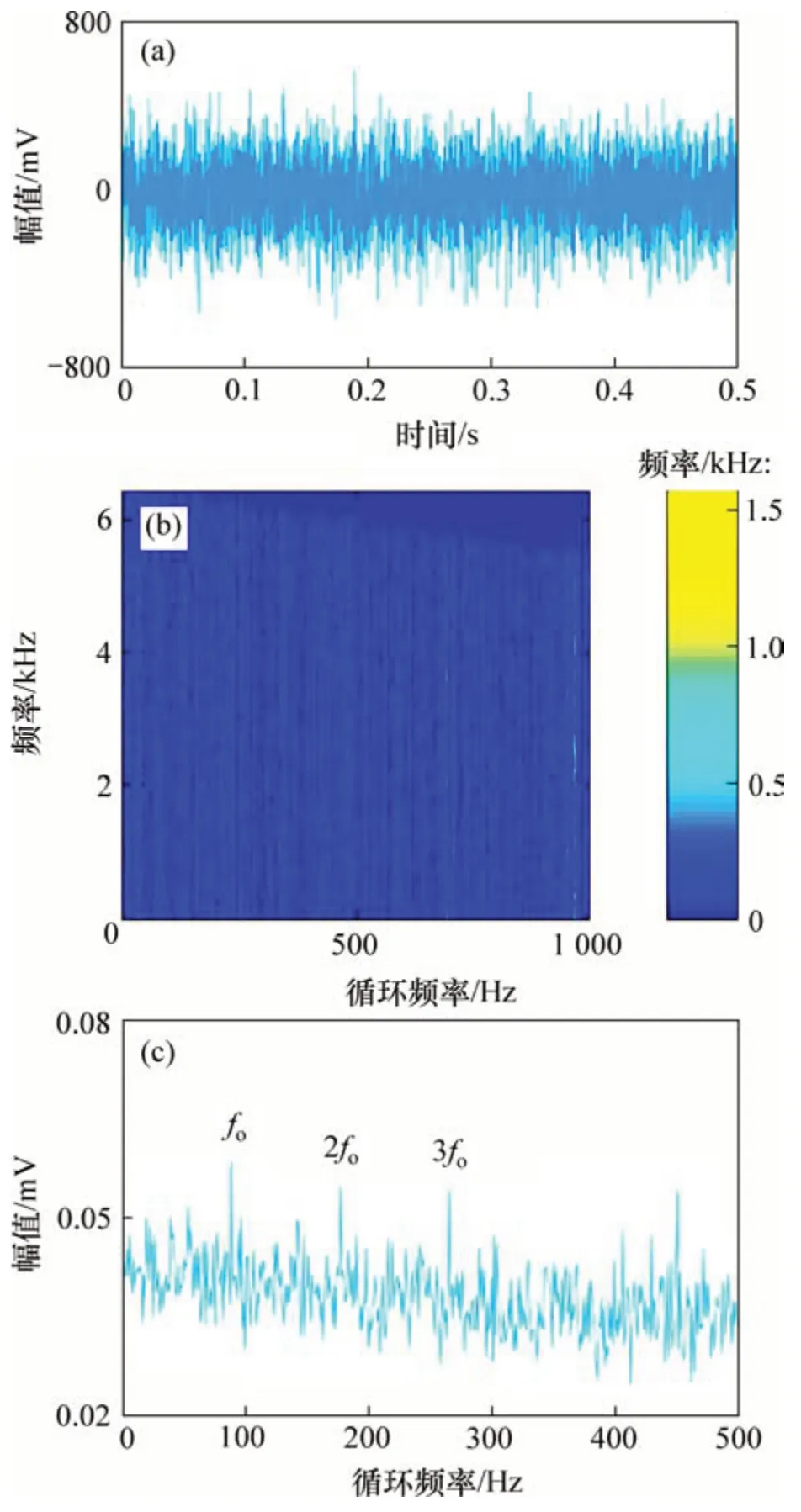
圖10 本文提出方法的分析結(jié)果Fig.10 Analysis results of proposed method

圖9(a)和9(b)所示分別為實驗采集的振動信號時域波形及其包絡譜。包絡譜中有2倍和3倍的外圈故障頻率(2fo和3fo)的諧波出現(xiàn)，但諧波幅值不突出，容易誤診為噪聲頻率。使用本文方法對實驗信號進行分析。圖10(a)，(b)和(c)所示分別為NLM去噪后信號時域波形、去噪信號的快速譜相關(guān)譜以及相關(guān)譜對應的增強包絡譜。由圖10(c)可知：外圈故障頻率(fo)、2 倍頻(2fo)和3 倍頻(3fo)的諧波被有效提取，且幅值突出不會被誤診為噪聲頻率。分別使用FSC 方法，SK-NLM 方法以及NLMEMD 方法對實驗信號進行分析，說明本文方法的優(yōu)越性，圖11、圖12和圖13所示分別為FSC 方法、SK-NLM方法和NLM-EMD方法的分析結(jié)果。由圖11(b)可知：FSC方法可以提取出2倍和3倍的外圈故障頻率(2fo和3fo)的諧波，但特征頻率幅值與噪聲頻率相比并不突出，容易導致誤診。由圖12(c)和圖13(c)可知：SK-NLM方法和NLM-EMD方法無法提取出外圈故障頻率及其諧波。經(jīng)分析可知：造成SK-NLM 方法無法提取故障特征是由于譜峭度方法容易受到隨機沖擊噪聲的干擾，構(gòu)造出的帶通濾波器只對隨機沖擊敏感，不能濾出周期沖擊信號。對濾出的窄帶信號進行NLM 降噪，也無法提取出故障特征(即周期沖擊頻率)。造成NLM-EMD方法無法提取故障特征是由于NLM算法對強噪聲信號(如軸承早期故障振動信號)的處理效果不理想，加之EMD 算法自身存在模態(tài)混疊和端點效應等缺點，導致無法實現(xiàn)特征提取。上述分析結(jié)果表明，相較于快速譜相關(guān)方法、SKNLM方法以及NLM-EMD方法，本文方法可以抑制噪聲干擾，有效提取故障特征，準確診斷故障類型。

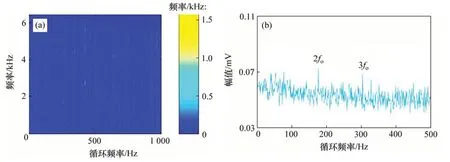
圖11 快速譜相關(guān)方法的分析結(jié)果Fig.11 Analysis results of FSC method

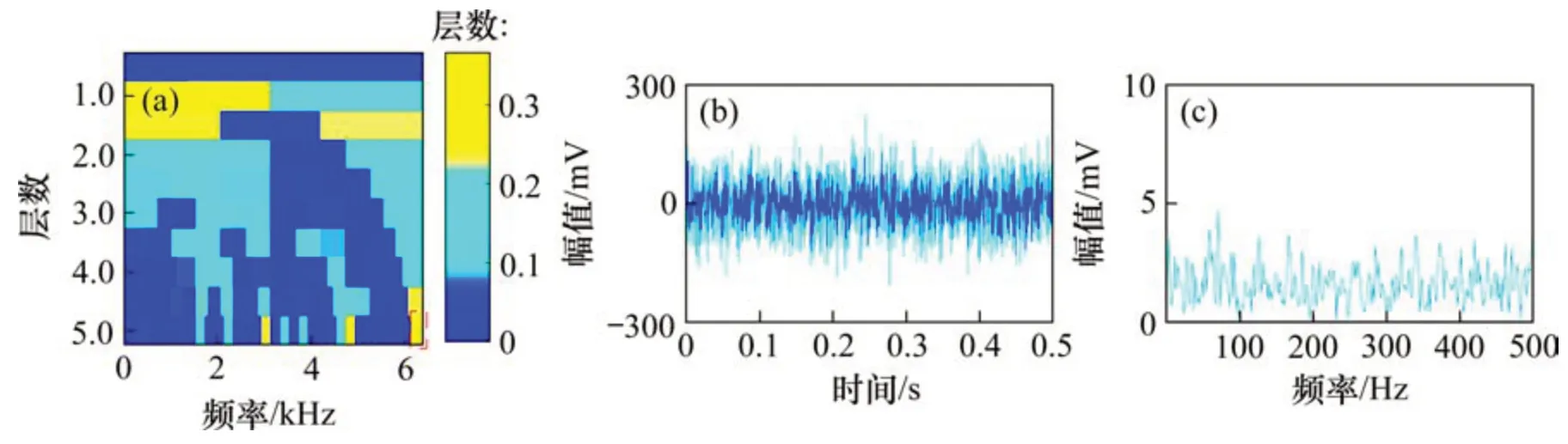
圖12 SK-NLM方法的分析結(jié)果Fig.12 Analysis results of SK-NLM method

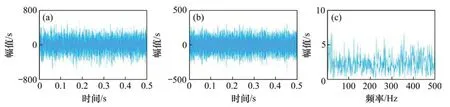
圖13 NLM-EMD方法的分析結(jié)果Fig.13 Analysis results of NLM-EMD method

5 結(jié)論

1)提出基于NLM-FSC的滾動軸承早期故障診斷方法，利用非局部均值去噪算法降低噪聲干擾，提高信號信噪比，結(jié)合快速譜相關(guān)算法增強信號中的周期成分，有效提取出微弱故障特征，準確判斷故障類型。

2)使用本文方法對仿真故障信號、實驗故障信號進行分析，結(jié)果表明所提出的方法是有效的。

3)將FSC 方法、SK-NLM 方法和NLM-EMD方法進行對比分析，結(jié)果表明所提出方法的分析效果優(yōu)于直接使用FSC 方法的分析效果，并且可以避免由于SK 算法易受隨機沖擊噪聲干擾以及NLM 算法處理信噪比低、信號效果差而造成的誤診。