斜拉索損傷對在役斜拉橋體系可靠度的影響

顏東煌，郭鑫,2

(1.長沙理工大學(xué)土木工程學(xué)院，湖南長沙，410114；2.長沙理工大學(xué)長沙理工大公路工程試驗檢測中心，湖南長沙，410007)

斜拉橋具有跨越能力大、經(jīng)濟性能好、外觀優(yōu)美等優(yōu)點，是中大跨度橋梁的首選橋型。我國建設(shè)了一大批混凝土斜拉橋，主跨最大達1 088 m。然而，在役斜拉橋運營期間出現(xiàn)了一系列耐久性問題，如拉索腐蝕、錨頭銹蝕、索力損失等。其中，由于拉索腐蝕導(dǎo)致的拉索壽命較低的現(xiàn)象是威脅斜拉橋運營安全的主要問題，且拉索全部更換的造價往往達到施工成本的5倍以上，甚至超出全橋造價。準(zhǔn)確評估斜拉索腐蝕情況下斜拉橋結(jié)構(gòu)體系的安全性，為拉索更換提供理論基礎(chǔ)。許多研究者通過斜拉索腐蝕疲勞試驗研究了拉索腐蝕后的力學(xué)性能[1]、疲勞強度[2]和剩余壽命[3]。在斜拉索腐蝕后的抗力概率模型方面，F(xiàn)ABER等[4]在平行鋼絲腐蝕疲勞試驗的基礎(chǔ)上，研究了拉索的剩余承載力與強度概率模型，認(rèn)為腐蝕疲勞復(fù)合因素作用下鋼絲數(shù)量與長度效應(yīng)對拉索強度均值的影響分別達10% 和8%。LAN 等[5-6]采用Monte Carlo 抽樣方法對斜拉索疲勞壽命概率特征進行研究，發(fā)現(xiàn)斜拉索的疲勞壽命由短索的斷裂控制。蘭成明等[7]采用PSN曲線和等效損傷路徑方法研究了斜拉索疲勞壽命的概率分布函數(shù)，認(rèn)為鋼絲數(shù)量增加會減小其疲勞壽命的變異性，而疲勞壽命均值基本不受影響。由于斜拉橋是超靜定結(jié)構(gòu)體系，單根拉索的斷裂并不致使橋梁倒塌，因此，人們對斜拉索腐蝕后斜拉橋的安全問題進行了研究。LI等[8]研究了高強鋼絲腐蝕疲勞對斜拉橋剩余承載力的影響，據(jù)此評估了南京長江三橋的承載力。劉沐宇等[9]研究了斜拉索疲勞損傷對斜拉橋可靠度的影響。魯乃唯等[10]采用聯(lián)合智能算法分析了斜拉橋運營期的主要失效路徑，認(rèn)為首要失效路徑是邊跨拉索斷裂導(dǎo)致索塔彎曲破壞，其次是中跨拉索斷裂導(dǎo)致跨中主梁破壞。LU 等[11]提出了基于支持向量回歸的斜拉橋時變體系可靠度分析方法。然而，斜拉索的腐蝕疲勞損傷對斜拉橋體系可靠度影響機理尚未明確，為此，本文作者對在役斜拉橋的斜拉索腐蝕疲勞損傷對其體系可靠度的影響進行研究。首先，建立腐蝕拉索疲勞損傷后的剩余強度概率模型；其次，提出一種能夠捕捉拉索強度退化對斜拉橋體系失效路徑影響的高效分析方法；最后，以某雙塔混凝土斜拉橋為例，分析斜拉索腐蝕對其體系可靠度的影響規(guī)律。研究結(jié)果可為在役斜拉橋的安全評定與換索決策提供依據(jù)。

1 平行鋼絲索的靜力強度

斜拉索的靜力強度模型需要考慮2 方面的因素[12]：首先是單根細(xì)長鋼絲的多點坑蝕導(dǎo)致的材料強度下降問題即長度效應(yīng)問題；其次是平行鋼絲數(shù)量增加導(dǎo)致其強度下降的因素（即丹尼爾效應(yīng)問題）。

1.1 單根鋼絲的靜力強度

將單根鋼絲沿其長度方向劃分為若干個單元，則該鋼絲的強度與單元的數(shù)量和鋼絲的長度有關(guān)，形成一個串聯(lián)系統(tǒng)。顯然，單根鋼絲的強度由其最薄弱的節(jié)段所決定。

鋼絲材料的缺陷或者腐蝕等因素引起的損傷對鋼絲靜力強度的影響均可通過相關(guān)系數(shù)ρ表示(0<ρ<1)。ρ接近于1表示鋼絲缺陷較少，ρ接近于0表示鋼絲缺陷較多。引入相關(guān)長度參數(shù)Lρ，Lρ=lL0(其中，L0為試驗樣本鋼絲的長度；l為系數(shù)，l大于1 表示相關(guān)長度大于試驗樣本長度，即串-并聯(lián)模型中的單元數(shù)量可減小；l小于1 表示相關(guān)長度大于試驗樣本長度，即串-并聯(lián)模型的單元數(shù)量應(yīng)增加)。

假定某鋼絲可劃分為m個單元，且單元之間具有一定的相關(guān)性，則鋼絲的強度可表示為

式中：Zi為第i個單元的強度。FABER 等[4]進行鋼絲靜力試驗時發(fā)現(xiàn)鋼絲強度服從Weibull 分布FZi(z)：

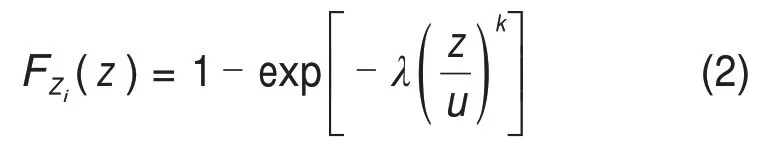
式中：z為斜拉索的強度；λ，u和k分別為Weibull分布函數(shù)的尺度、位置和形狀參數(shù)。上述參數(shù)可采用鋼絲樣本的靜力強度試驗結(jié)果，由最大似然估計方法得出近似解。

1.2 平行鋼絲索的靜力強度

當(dāng)斜拉索鋼絲的數(shù)量足夠大時，平行鋼絲索的強度服從正態(tài)分布，拉索強度均值可表示為

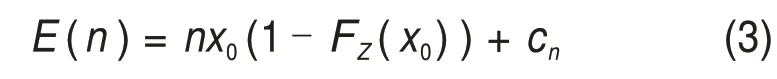
式中：n為鋼絲數(shù)量；cn=0.966an1/3；a3=σu為均斜拉索鋼絲的極限強度；L為拉索總長。相應(yīng)地，標(biāo)準(zhǔn)差Dn可表示為

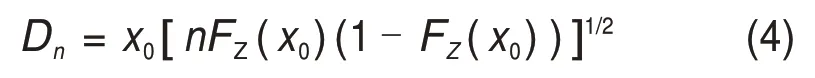
式中：cn為由于拉索數(shù)量引起的附加相關(guān)項，當(dāng)n大于150 時，該數(shù)值可忽略；而當(dāng)n小于150 時，cn可表示為數(shù)量效應(yīng)的修正系數(shù)[13]。

需說明的是：斜拉索損傷的量化與其損傷程度有較大關(guān)系，拉索運營期腐蝕損傷程度有多種劃分方法[14]，JTG/T-H21—2011“公路橋梁技術(shù)狀況評定標(biāo)準(zhǔn)”給出了5 個等級的鋼絲分級及描述。為了研究腐蝕對斜拉索強度退化概率的影響，本文采用前4 個損傷等級，即鋼絲狀態(tài)處于“完好”至“密集蝕坑”之間。

1.3 算例分析

假定拉索鋼絲樣本數(shù)量為30個[4]，樣本極限強度均值σu=1 788.7 MPa，Weibull 模型的分布參數(shù)k=72.62，假定比例因子ξ(即L/L0)分別為1，3 和10，則拉索鋼絲數(shù)量從10 根變化至300 根的斜拉索強度退化模型如圖1所示。

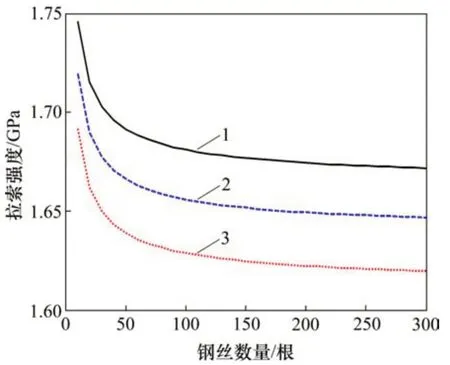
圖1 鋼絲數(shù)量對斜拉索強度的影響Fig.1 Influence of number of wire on cable-stay strength

由圖1可知：斜拉索強度隨著鋼絲數(shù)量增加有所下降，且隨著比例因子ξ增加而下降；當(dāng)ξ=10時，鋼絲數(shù)量由10 根增加至300 根導(dǎo)致斜拉索強度下降4.3%。在1根斜拉索的鋼絲數(shù)量為300根的情況下，比例因子ξ由1提高至10將導(dǎo)致斜拉索強度下降約3%。

LI 等[15]對運營20 a 的69 根腐蝕平行鋼絲索與13 根未腐蝕平行鋼絲索進行疲勞試驗研究，采用樣本長度l0=0.5 m的鋼絲，鋼絲樣本的強度概率密度曲線如圖2所示。基于文獻[4]中的鋼絲樣本的強度概率模型，考慮長度為232 m、數(shù)量n=243 根的某實橋斜拉索。該斜拉索設(shè)計強度σb=1 766 MPa，則由式(3)和式(4)可得到該斜拉索的強度退化概率模型如圖3所示。

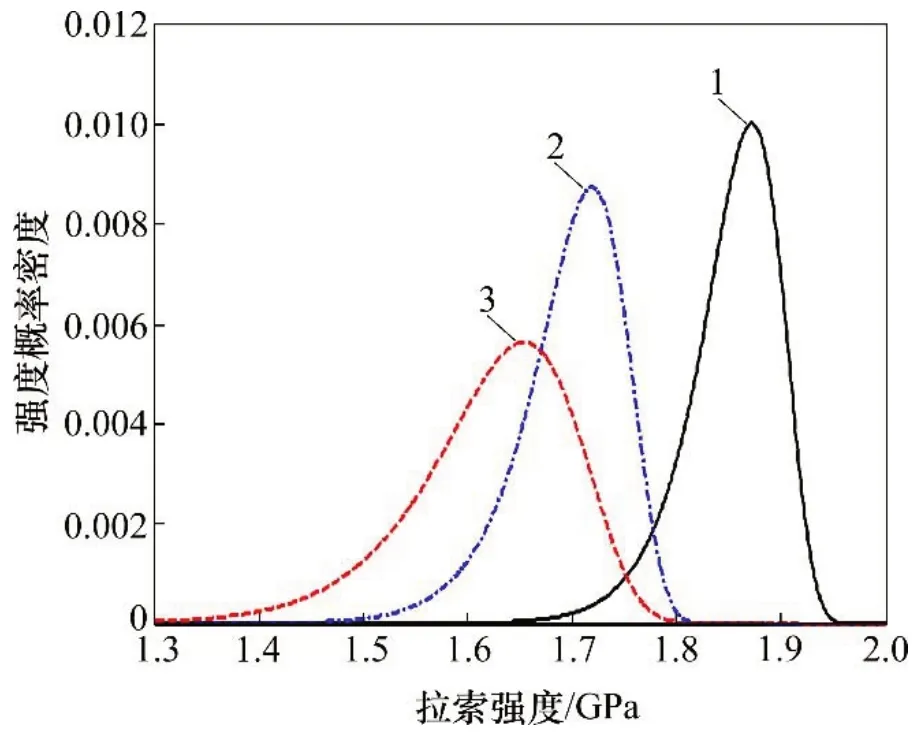
圖2 短鋼絲樣本的試驗強度概率密度曲線Fig.2 Probability density curves of tested strength of short cable specimem

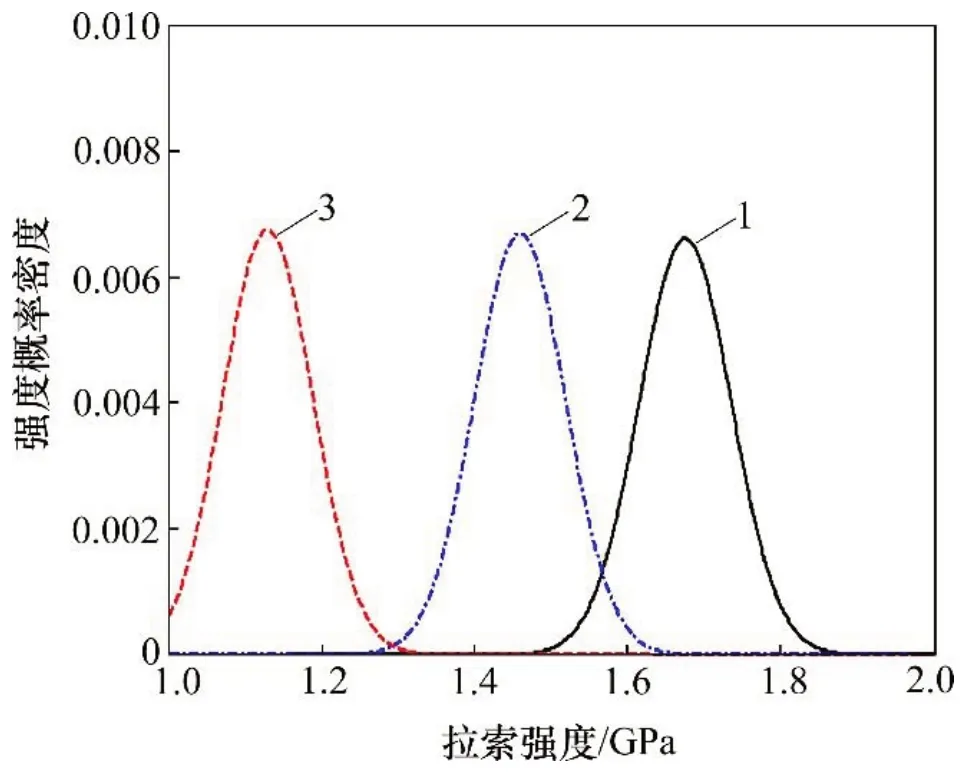
圖3 斜拉索的強度概率模型Fig.3 Probabilistic model of cable strength

圖3中，σc,c，σu,c和σn,c分別表示腐蝕拉索、未腐蝕拉索和新索的抗拉強度。拉索運營20 a 后，腐蝕拉索和未腐蝕拉索的強度相對新拉索分別下降32%和13%，而標(biāo)準(zhǔn)差下降幅度不到2%。由此可知，拉索數(shù)量和長度效應(yīng)導(dǎo)致的拉索強度變異系數(shù)相對于均值而言可忽略不計。

2 斜拉橋時變失效路徑搜索方法

2.1 斜拉橋結(jié)構(gòu)體系特征

斜拉橋是由斜拉索、主梁、索塔等多個構(gòu)件組成的超靜定結(jié)構(gòu)體系。斜拉橋的體系失效是一連串構(gòu)件失效所致，因此，關(guān)鍵失效路徑的各單元強度退化將改變失效路徑。

考慮斜拉索強度時變特性導(dǎo)致的結(jié)構(gòu)體系時變失效路徑搜索的關(guān)鍵點如下[16]。

1)斜拉橋結(jié)構(gòu)體系的非線性行為。斜拉索的垂度效應(yīng)與梁柱效應(yīng)具有非線性行為，斜拉索不僅強度退化，而且其彈性模量也將發(fā)生改變。采用非線性功能函數(shù)捕捉結(jié)構(gòu)的非線性行為將影響計算精度與效率。

2)一種搜索斜拉橋結(jié)構(gòu)體系主要失效路徑的高效方法。斜拉橋結(jié)構(gòu)超靜定次數(shù)較多，失效路徑多，關(guān)鍵失效路徑是影響效應(yīng)效率的關(guān)鍵所在。

3)如何考慮斜拉索的時變抗力退化參數(shù)對斜拉橋結(jié)構(gòu)體系時變可靠度的影響，識別拉索強度退化如何導(dǎo)致結(jié)構(gòu)體系失效路徑轉(zhuǎn)移。

2.2 基于更新響應(yīng)面的失效路徑搜索方法

針對上述關(guān)鍵點，本文基于文獻[17]所提出的更新支持向量方法，采用一種更新響應(yīng)面方法與β約界法相結(jié)合的實用分析方法，用于搜索斜拉橋時變體系的失效路徑。相對于更新支持向量方法而言，本文所提出的更新響應(yīng)面方法更加簡單、明確，但對線性的捕捉精度可能比更新支持方向方法的低。該方法的分析流程如圖4所示，其中，T和Ts分別表示當(dāng)前步驟計算時間和橋梁設(shè)計壽命。

圖4所示流程圖的關(guān)鍵步驟如下：

1)通過結(jié)構(gòu)的參數(shù)敏感分析，篩選影響結(jié)構(gòu)主要失效模式的關(guān)鍵隨機變量，如荷載、拉索彈模、混凝土容重等。

2)采用二次序列響應(yīng)面方法擬合隨機變量與橋梁關(guān)鍵構(gòu)件響應(yīng)之間的函數(shù)關(guān)系，由Monte Carlo抽樣方法計算各關(guān)鍵構(gòu)件的可靠指標(biāo)。

3)采用β 約界方法搜索關(guān)鍵構(gòu)件的失效單元，并對失效單元進行處理。若構(gòu)件發(fā)生脆性破壞，則刪除失效單元；若構(gòu)件發(fā)生塑性破壞，則增加塑性鉸。

4)基于斜拉橋新結(jié)構(gòu)更新響應(yīng)面，重復(fù)步驟2)和3)，直至結(jié)構(gòu)體系失效，再構(gòu)建結(jié)構(gòu)的失效樹。

5)考慮斜拉索腐蝕導(dǎo)致的抗力退化概率模型，更新斜拉索參數(shù)，返回步驟1)。

6)計算時間達到斜拉索設(shè)計年限(20～30 a)時結(jié)束。

采用如圖4所示的更新響應(yīng)面方法分析斜拉橋體系可靠度的優(yōu)勢在于：

1)采用二次序列響應(yīng)面函數(shù)來擬合斜拉橋構(gòu)件的荷載效應(yīng)，可捕捉其一定程度的非線性效應(yīng)，如拉索垂度效應(yīng)、梁柱效應(yīng)及大變形等，詳細(xì)內(nèi)容見文獻[18]。

2)采用β約界方法搜索潛在失效單元，并以更新響應(yīng)面的方法擬合單元失效后的新結(jié)構(gòu)功能函數(shù)，捕捉到單元失效后結(jié)構(gòu)體系的特性。

3)考慮斜拉索抗力退化，再次更新斜拉橋有限元模型，重新對失效構(gòu)件進行篩選分析。雖然計算較繁瑣，但可捕捉斜拉索抗力退化對結(jié)構(gòu)體系可靠度的影響。

3 雙塔混凝土斜拉橋可靠度研究

3.1 工程背景

某斜拉橋的跨徑為(210+420+210) m，結(jié)構(gòu)體系為剛構(gòu)體系，雙塔混凝土π型主梁結(jié)構(gòu)[18]。主梁為C60混凝土材料，主塔為C50混凝土材料，斜拉索為鋼絞線。主梁與斜拉索均為34 對，橋面寬度為30 m，雙向6 車道，按照公路-I 級汽車荷載設(shè)計。橋梁的結(jié)構(gòu)尺寸如圖5所示。圖5中：為中跨第1 至第34 號拉索，為邊中第1 號至第34號拉索，表示邊跨第1號至第34號主梁，表示中跨第1號至第34號主梁；P1與P2為索塔的彎曲失效控制點，P3為主梁彎曲失效控制點。

3.2 確定性結(jié)構(gòu)分析

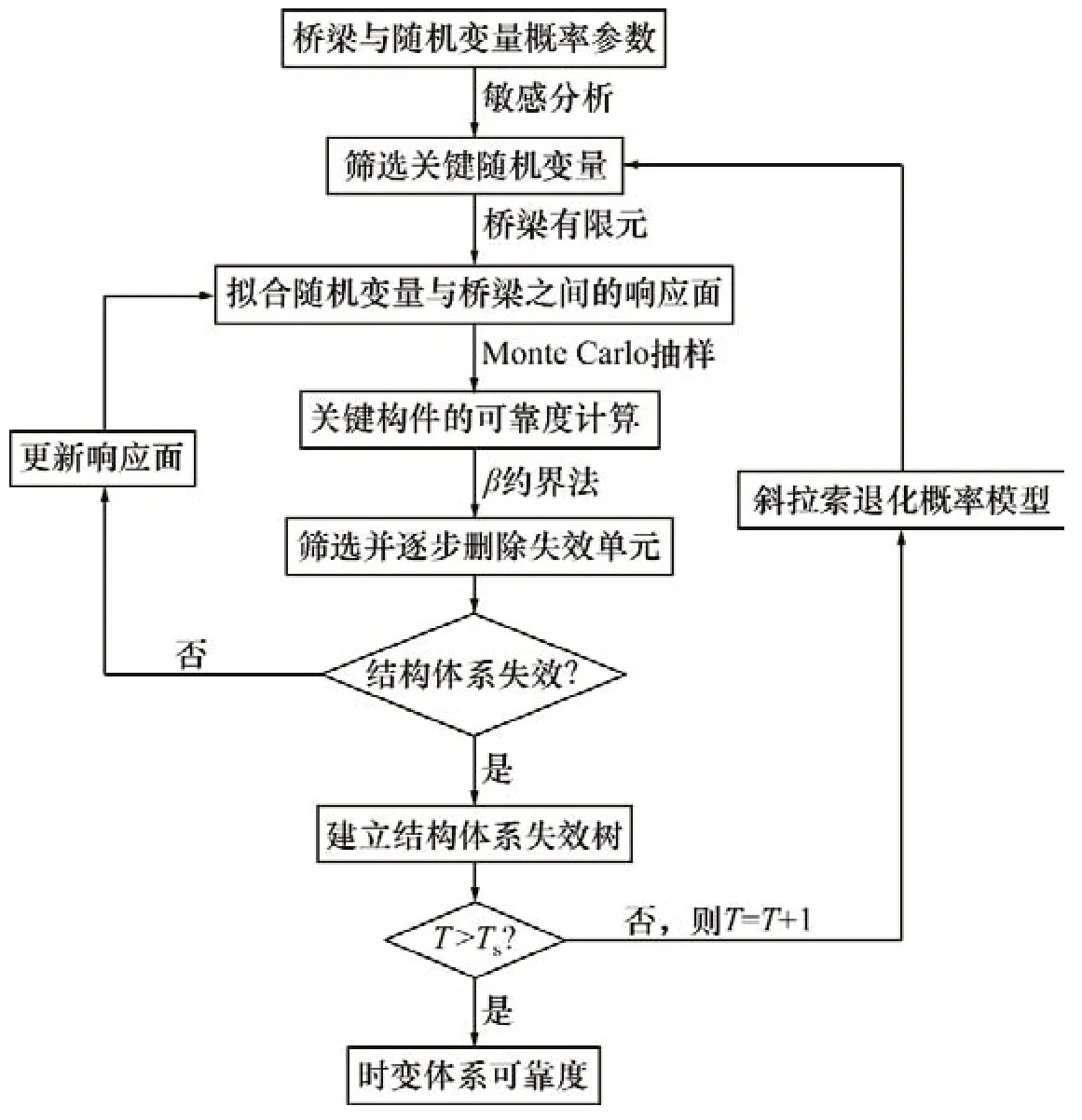
圖4 考慮斜拉索損傷的斜拉橋失效路徑搜索流程Fig.4 Flowchart for searching failure sequences of cable-stayed bridges considering cable damage

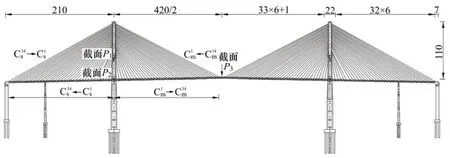
圖5 斜拉橋結(jié)構(gòu)尺寸與單元劃分圖Fig.5 Structural dimension and elements division of cable-stayed bridge

采用有限元軟件ANSYS 建立橋梁的有限元模型，如圖6所示，其中，斜拉索采用LINK180 單元，主梁與索塔均采用BEAM188單元。考慮最不利車輛荷載以均布荷載的形式加載至橋梁。根據(jù)文獻[18]中分析結(jié)果，斜拉橋最易失效的拉索是最長索。文獻[19]的研究結(jié)果表明銹蝕斷絲對斜拉索的力學(xué)性能有較大影響。針對本斜拉橋，選取中跨34 號拉索為例，分析該斜拉索斷裂之后相鄰拉索33，32和31號拉索索力及主梁與索塔關(guān)鍵截面彎矩的變化。

圖6 斜拉橋有限元模型Fig.6 Finite element model of cable-stayed bridge

在ANSYS 前處理模塊刪除C34m拉索，并在34號主梁施加與索力和拉索角度相同的集中力；然后進入瞬態(tài)分析模塊，在0 s 進行當(dāng)前狀態(tài)分析，在0.1 s施加與索力數(shù)值相同、方向相反的集中力，以模擬斷索效應(yīng)；記錄25 s以內(nèi)的關(guān)鍵構(gòu)件效應(yīng)時程曲線，如圖7所示。

基于圖7所示的動力時程曲線，將靜力和動力效應(yīng)最大值與原始效應(yīng)值進行對比，得到拉索失效引起的靜力與動力增大系數(shù)如表1所示。表1中，δs與δd分別表示C34m拉索斷裂后關(guān)鍵構(gòu)件的靜力與動力增大系數(shù)。由表1可以看出：斜拉索斷裂不僅導(dǎo)致相鄰構(gòu)件的內(nèi)力增加，而且其動力放大效應(yīng)不可忽略，如C44m拉索斷裂導(dǎo)致C33m拉索索力的靜力效應(yīng)增加0.07，而動力效應(yīng)最大值達到0.11，為靜力效應(yīng)的84%；離失效拉索較近的構(gòu)件的放大系數(shù)大，而離失效拉索較遠的構(gòu)件的放大系數(shù)較小。

3.3 響應(yīng)面擬合與更新

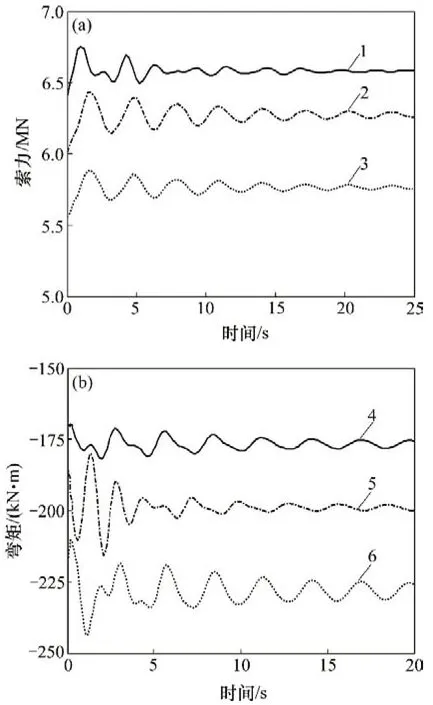
圖7 跨中34號單側(cè)斜拉索失效后關(guān)鍵構(gòu)件響應(yīng)時程曲線Fig.7 Time-history curves of response of the key components considering Cm34 cable failure

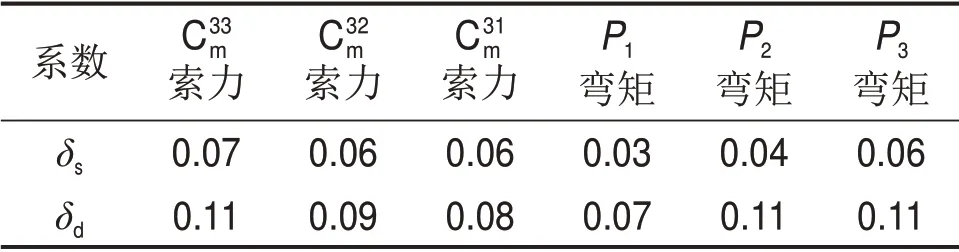
表1 C3m4 拉索斷裂后關(guān)鍵構(gòu)件內(nèi)力放大系數(shù)Table 1 Amplification factor of inter-force of critical members due to C3m4 cable rupture

采用如圖4所示的基于響應(yīng)面方法的失效路徑搜索方法擬合斜拉索索力的響應(yīng)面，其關(guān)鍵步驟為：首先，由均勻設(shè)計的1批樣本點數(shù)據(jù)計算結(jié)構(gòu)的非線性效應(yīng)；由二次序列響應(yīng)面擬合樣本曲面，形成如圖8所示的響應(yīng)面；在有限元模型中刪除潛在失效構(gòu)件，繼續(xù)進行結(jié)構(gòu)分析與響應(yīng)面擬合。根據(jù)上述步驟即可捕捉到斜拉索逐步失效導(dǎo)致的結(jié)構(gòu)非線性效應(yīng)。為了分析C34m拉索斷裂前后的C33m拉索索力的響應(yīng)面，選取拉索截面面積As、汽車均布荷載Q為隨機變量，采用20個樣本的U202均勻設(shè)計樣本方案，擬合C33m拉索索力更新前后的響應(yīng)面，如圖8所示，其中，為索力，U20-2 表示均勻設(shè)計表中對應(yīng)的樣本數(shù)量為20 個，參數(shù)為2個。

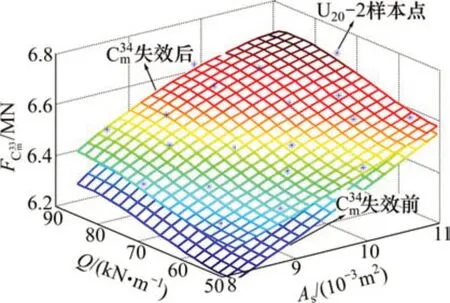
圖8 C34m 拉索失效前后的C33m 拉索索力響應(yīng)面Fig.8 Response surfaces of stay cable force of C33m cable affected by C34m cable failure

由圖8可知：斜拉索索力響應(yīng)面邊緣呈現(xiàn)非線性特征，僅采用20 個樣本點即可捕捉到該非線性響應(yīng)。雖然斜拉橋在正常使用狀態(tài)下的非線性特征不顯著，但在極限狀態(tài)下的結(jié)構(gòu)行為表現(xiàn)出一定的非線性。此外，采用更新響應(yīng)面方法可捕捉到拉索斷裂引起的內(nèi)力變化。

基于更新響應(yīng)面方法，逐步更新結(jié)構(gòu)關(guān)鍵構(gòu)件的失效構(gòu)件響應(yīng)面，直到搜索到斜拉橋結(jié)構(gòu)體系的全部失效路徑，并計算相關(guān)系數(shù)。該斜拉橋在第20年的結(jié)構(gòu)體系失效樹如圖9所示，圖中βs,i表示第i個失效路徑的可靠指標(biāo)。

結(jié)合圖3所示的斜拉索強度退化概率模型與圖9所示失效樹，考慮斜拉索的“疲勞”和“腐蝕-疲勞”這2種損傷狀態(tài)，斜拉橋的結(jié)構(gòu)體系可靠度的時變趨勢如圖10所示。

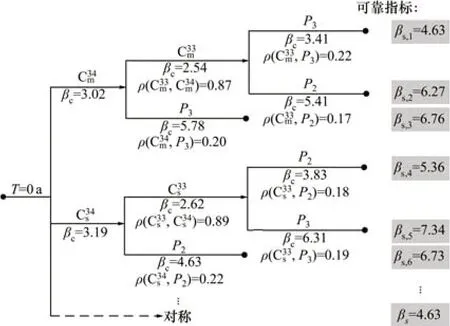
圖9 斜拉橋結(jié)構(gòu)體系失效樹Fig.9 Fault tree of structural system of cable stayed bridge

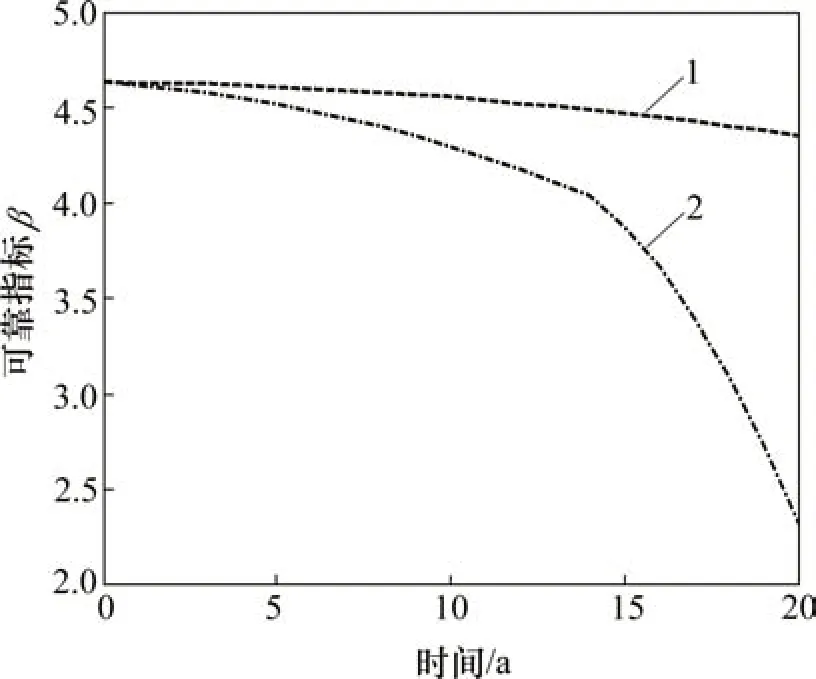
圖10 斜拉橋時變體系可靠度Fig.10 Time-variant system reliability of cable-stayed bridge

由圖10可知：在“疲勞”和“腐蝕-疲勞”這2種損傷作用下，該斜拉橋在第20年的結(jié)構(gòu)體系可靠指標(biāo)由4.62分別下降至4.42和和2.46，表明腐蝕與疲勞2種損傷的復(fù)合作用導(dǎo)致斜拉橋體系可靠度下降趨勢較顯著。

4 結(jié)論

1) 腐蝕和未腐蝕拉索在20 a 后的抗拉強度均值分別下降32%和13%，而標(biāo)準(zhǔn)差下降幅度均小于2%，表明基于串-并聯(lián)模型可捕捉鋼絲長度和數(shù)量效應(yīng)對拉索強度概率分布均值和標(biāo)準(zhǔn)差的影響。

2)單根拉索斷裂可導(dǎo)致相鄰拉索索力靜力效應(yīng)增加7%，而動力效應(yīng)達到11%，基于更新響應(yīng)面方法采用20 個均勻設(shè)計樣本點即可捕捉到該非線性效應(yīng)。

3)在“疲勞”和“腐蝕-疲勞”這2 種損傷作用下，該斜拉橋在第20年的結(jié)構(gòu)體系可靠指標(biāo)由4.62分別下降至4.42和和2.46，表明腐蝕效應(yīng)對斜拉橋運營期體系可靠度影響顯著。