量子力學(xué)教學(xué)中Mathematica的簡單應(yīng)用

蒲 瑾

（西華師范大學(xué)物理與空間科學(xué)學(xué)院 四川南充 637002）

一、引言

量子力學(xué)是在20世紀(jì)初建立起來的以微觀粒子運(yùn)動規(guī)律為研究對象的一門重要理論。隨著量子理論的深入研究，其對現(xiàn)代物質(zhì)文明的發(fā)展發(fā)揮了舉足輕重的作用。我們不僅已經(jīng)見證了量子理論與麥克斯韋方程組偉大的結(jié)合，結(jié)果使得電磁場本質(zhì)的研究大放異彩，而且量子理論在量子信息科學(xué)、量子化學(xué)、量子生物學(xué)、材料科學(xué)、天體物理等領(lǐng)域中也被廣泛地應(yīng)用。因此，如何讓高等院校物理專業(yè)學(xué)生學(xué)好量子力學(xué)，是高校量子力學(xué)教師非常值得研究的一個重要課題[3-5]。

本文以一維諧振子和氫原子作為實(shí)例，闡述Mathematica軟件在量子力學(xué)教學(xué)中的應(yīng)用，復(fù)雜、抽象的公式被簡單地圖形化、可視化。這樣，學(xué)生對量子力學(xué)物理本質(zhì)的認(rèn)識更加深刻，有助于增強(qiáng)學(xué)生的學(xué)習(xí)信心、激發(fā)學(xué)習(xí)動力。

二、在量子力學(xué)教學(xué)中Mathematica的應(yīng)用實(shí)例

由于簡諧運(yùn)動在自然界中廣泛地存在，它往往是被看做復(fù)雜運(yùn)動的簡單近似，因此，在理論和應(yīng)用上研究諧振子運(yùn)動都具有非常重要的意義[1-2]。設(shè)一維線性諧振子的勢能為V(x)=mω2x2/2，則體系的薛定諤方程為：

很顯然，由于束縛態(tài)的邊界條件引起諧振子能量的量子化，并且其能級的分布是均勻的，即相鄰能級間距為?ω。歸一化的能量本征函數(shù)為：

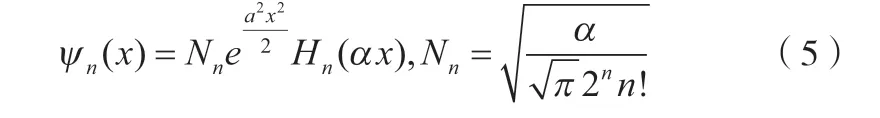
式中Hn(αx)是Hermite多項(xiàng)式。利用Mathematica編寫程序繪制出本征函數(shù)ψn(x)和概率密度ωn(x)的分布圖像，如圖1所示。圖中取α=1，實(shí)和虛曲線分別表示本征函數(shù)和概率密度。圖中可以直觀地反映出量子力學(xué)中線性諧振子的運(yùn)動規(guī)律，有助于學(xué)生深刻理解這部分知識。同時，程序編寫非常簡單，直接調(diào)用程序中HermiteH[n,x]就可以輕松畫出Hermite多項(xiàng)式。以n=3為例，Mathematica輸入程序如下：

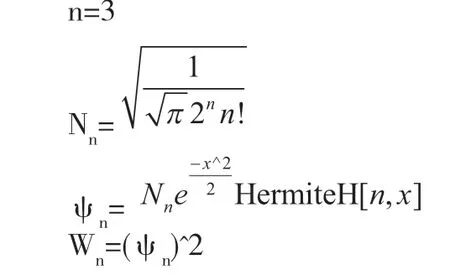
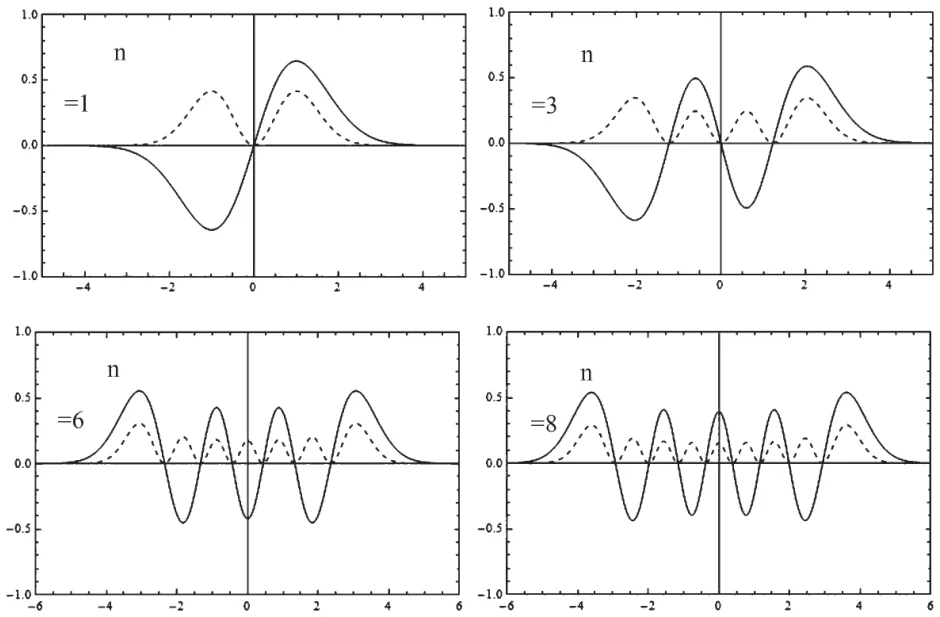
圖1 能量本征函數(shù)和概率密度圖

氫原子不僅可以通過薛定諤方程嚴(yán)格求解，而且是量子力學(xué)發(fā)展史上最突出的成就之一[1-2]。同時，氫原子是最簡單的原子，是研究復(fù)雜原子和分子結(jié)構(gòu)的基礎(chǔ)[1-2]。讓學(xué)生掌握通過薛定諤方程求解氫原子的能級和波函數(shù)的方法是非常重要的，但這個求解的過程比較復(fù)雜，講解起來學(xué)生覺得非常枯燥，且結(jié)果也非常抽象。因此，讓學(xué)生利用Mathematica來將結(jié)果圖形化，激發(fā)學(xué)生自主探究，達(dá)到提高學(xué)習(xí)效果的目的，就顯得非常重要。對于氫原子來說，原子核與電子之間的Coulomb勢為V(r)=-e2/r，則在自然單位下，具有一定角動量的氫原子徑向方程可表示為：

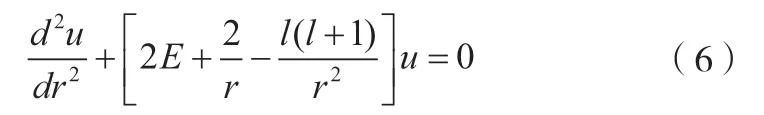
利用束縛態(tài)邊界條件，方程（6）化為一個合流超幾何方程。為了得到物理上的解，將無窮級數(shù)解F（-n+l+1，2l+2，2r/(na)）中斷為一個多項(xiàng)式，從而得到氫原子能級為En=-e2/(2an2)，其中a為玻爾半徑，主量子數(shù)n=1，2，3，…，角量子數(shù)l=0，1，2，…，n-1。徑向函數(shù)為：

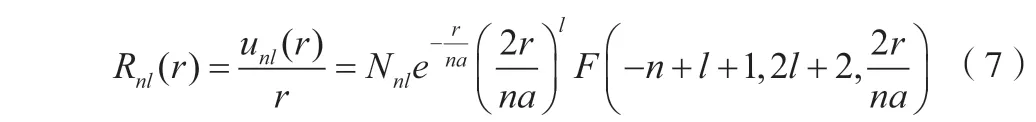
其中Nnl是歸一化因子。于是，利用Mathematica可以畫出氫原子中電子的徑向概率分布，如圖2所示。以n=3，l=1為例，采用原子單位，Mathematica輸入程序如下：

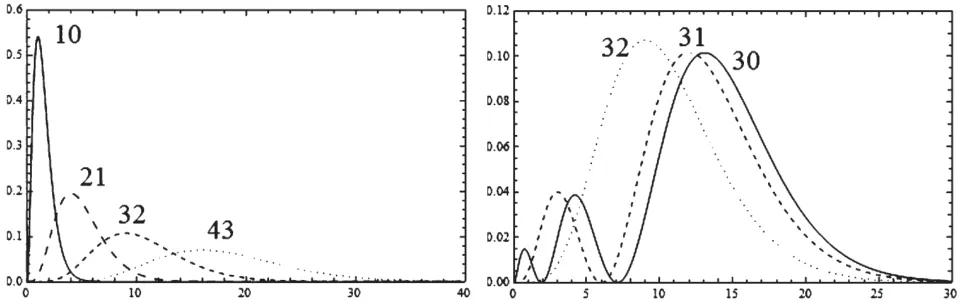
圖2 氫原子中電子的徑向概率分布圖

通過讓學(xué)生自己畫圖和觀察圖形，讓學(xué)生理解量子力學(xué)中電子的位置呈概率分布，即電子并無嚴(yán)格軌道的概念。同時，通過觀察徑向概率分布曲線隨量子數(shù)n和l的變化關(guān)系，進(jìn)一步理解氫原子結(jié)構(gòu)的特征。比如，徑向波函數(shù)的節(jié)點(diǎn)數(shù)目在不包括無窮遠(yuǎn)點(diǎn)與原點(diǎn)時，滿足nr=(n-l-1)關(guān)系[1-2]。在給定n時，l=n-1，nr=0的軌道對應(yīng)的徑向概率分布的最概然半徑滿足r=n2a[1]。

三、結(jié)束語

量子力學(xué)中存在許多的復(fù)雜計(jì)算和抽象結(jié)果，都可以利用Mathematica進(jìn)行快速計(jì)算和圖形化展示。本文只列舉了較突出的一維諧振子和氫原子的問題，事實(shí)上，還可以利用Mathematica在量子力學(xué)教學(xué)過程中進(jìn)行更多的科學(xué)計(jì)算和精準(zhǔn)繪圖。這樣，量子力學(xué)的教學(xué)過程將更加有趣和生動，讓教師有更充足的時間去加強(qiáng)量子理論本質(zhì)的講解。同時，可以通過課后練習(xí)，讓學(xué)生動手去利用Mathematica進(jìn)行實(shí)際操作，從而提高教學(xué)質(zhì)量。