縮小樣本空間
——解決條件概率問題的鑰匙

龔衛東(特級教師)

條件概率的概念及相關計算公式在高中數學《選修2-3》中以較小的篇幅進行了簡單介紹,但卻是高中數學學習的難點,高考中偶有涉及,學生得分情況不盡人意．主要原因是學生沒有深刻領會“條件”發生后的影響,將樣本空間與條件發生前的樣本空間混為一談,如著名的三門問題,生男孩女孩問題等．

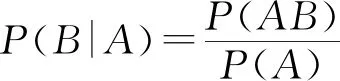
圖1

對定義給出的公式如果不能透徹理解,生搬硬套,就會產生很多疑問,從而得出如“抓鬮先后概率不同”等荒謬結論．本文結合教學實際經驗,給出基于韋恩圖(如圖1)總結解決條件概率問題的方法，即根據條件,縮小樣本空間,在新樣本空間中求后發生事件的概率．

例1從一副不含大小王的52張撲克牌中不放回地抽取2次,每次抽1張,已知第一次抽到A,求第二次也抽到A的概率.

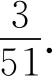
例2老王向老張介紹“這是我女兒”,老張問“你有幾個孩子?”老王答“3個”.求老王有兒子的概率.

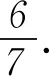
例3(2014年新課標卷Ⅱ理5) 某地區空氣質量監測資料表明,一天的空氣質量為優良的概率是0.75,連續兩天為優良的概率是0.6,已知某天的空氣質量為優良,那么隨后一天的空氣質量為優良的概率是( )．

A. 0.8 B. 0.75

C. 0.6 D. 0.45

解析 設一天的空氣質量為優良是事件A,連續兩天為優良是事件B,如圖1，本題所求的事件中，B一定是A的真子集，A是B的條件,則

例4(2015年北京卷文17) 某超市隨機選取1 000位顧客,記錄了他們購買甲、乙、丙、丁四種食品的情況,整理成統計表，如表1所示.其中“√”表示購買,“×”表示未購買.

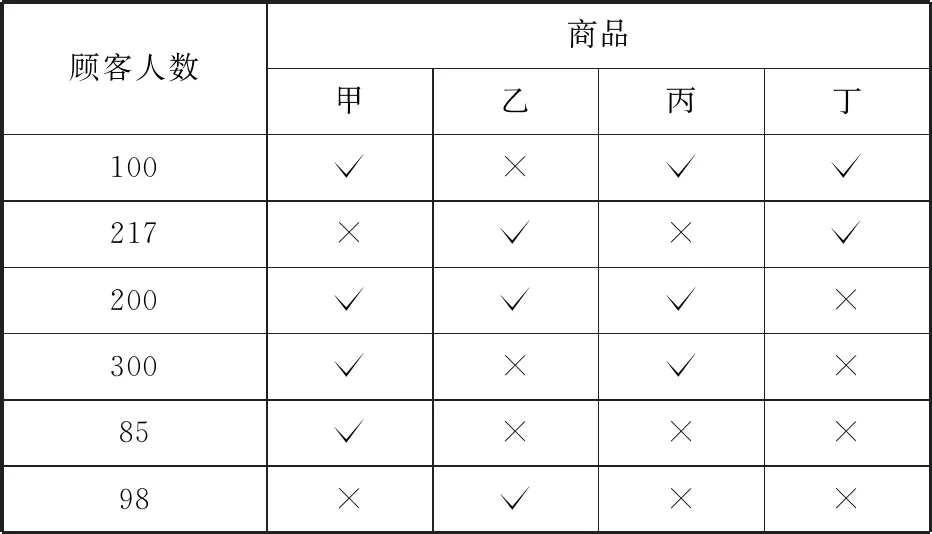
表1

(1)估計顧客同時購買乙和丙的概率；

(2)估計顧客在甲、乙、丙、丁中同時購買3種商品的概率；

(3)如果顧客購買了甲,則該顧客同時購買乙、丙、丁中哪種商品可能性最大？

解析 (1)0.2； (2)0.3(具體求解過程略).

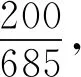
因此,顧客購買了甲,該顧客同時購買丙的可能性最大.

例5(2016年全國卷Ⅱ理18)某險種的基本保費為a(單位:元),繼續購買該險種的投保人稱為續保人,續保人本年度的保費與其上年度的出險次數的關聯如表2所示.

表2

設該險種一續保人一年內出險次數與相應概率如表3所示.

表3

(1)求一續保人本年度的保費高于基本保費的概率;

(2)若一續保人本年度的保費高于基本保費,求其保費比基本保費高出60%的概率.

解析 (1)設A表示事件:“一續保人本年度的保費高于基本保費”,則事件A發生當且僅當一年內出險次數大于1,故

P(A)=0.2+0.2+0.1+0.05=0.55.

(2)設B表示事件:“一續保人本年度的保費比基本保費高出60%”,則事件B發生當且僅當一年內出險次數大于3,故

P(B)=0.1+0.05=0.15.

又P(AB)=P(B),故

例6有一批種子的發芽率為0.9,出芽后的幼苗成活率為0.8,在這批種子中隨機抽取一粒,則這粒種子能成長為幼苗的概率是( ).

解析 本題中,設“發芽率”為事件A,出芽后的幼苗成活率0.8是條件概率P(B|A),“這粒種子能成長為幼苗”的含義是“發芽且長成幼苗”,其概率是P(AB),代入公式可得P(AB)=0.72,故選A.

由此可見,利用韋恩圖能夠幫助學生很好地理解條件的作用,條件越多,新樣本空間越小,后發事件在新樣本空間中的概率就會變大．以上問題基本囊括高中階段條件概率涉及的問題類型,基于韋恩圖,深刻理解條件,主動縮小樣本空間,就獲得了解決條件概率問題的鑰匙．