統計解題中經典錯解剖析
王小莉
統計是高中數學的重要內容,每年的高考中都有涉及,在求解與統計相關的問題時,學生常常會由于審題不嚴、考慮不周、忽視甚至挖掘不出題目的隱含條件等原因出現解題錯誤.本文就一些常見的問題加以剖析,以期幫助同學們避免出現同樣的錯誤.
1 對個體的入樣可能性理解不透
例1中央電視臺動畫城節目為了對本周的熱心觀眾給予獎勵,要從2 014名小觀眾中抽取50名幸運小觀眾.先用簡單隨機抽樣從2 014人中剔除14人,剩下的2 000人再按系統抽樣方法抽取50人,則在2 014人中,每個人被抽取的可能性( ).
A. 均不相等
B. 不全相等
錯解選A或D.
剖析對于選項A,常有學生誤認為剔除14人,被抽取到的機會就不相等了,從而錯選A;對于選項D,有的學生會認為被抽取的機會相等,但利用剔除后的數據計算,從而錯選D.

點睛系統抽樣具有等可能性,即每個個體被抽到的可能性相等.
2 忽略分層抽樣的特點
例2某單位有老年人28人,中年人54人,青年人81人,為了調查他們的身體情況,需從中抽取一個容量為36的樣本,則適合的抽樣方法是( ).
A. 簡單隨機抽樣
B. 系統抽樣
C. 直接運用分層抽樣
D. 先從老年人中剔除1人,再用分層抽樣

剖析如果用簡單隨機抽樣先從老年人中剔除1人,老年人被抽到的概率顯然比其他人群小了,這不符合隨機抽樣的特征——每個個體入樣的概率相等.注意錯解中明確地說“先從老年人中剔除1人”這和從總體中隨機剔除1人是不一樣的.

點睛分層抽樣的一個很重要的特點就是每個個體被抽到的概率相等.當按照比例計算出的值不是整數時,一般是采用四舍五入的方法取值,若四舍五入后得到的樣本容量與要求的不相同,則可根據問題的實際意義適當處理,使之相同,但不能改變分層抽樣的本質.
3 誤將頻率分布直方圖的縱坐標當作頻率
例3中小學生的視力狀況受到社會的關注.某市有關部門從全市6萬名高一學生中隨機抽取400名學生,對他們的視力狀況進行一次調查統計,將所得到的有關數據繪制成頻率分布直方圖,如圖1所示,從左至右五個小組的頻率之比為5∶7∶12∶10∶6,則該市6萬名高一學生中視力在[3.95,4.25)內的學生約有多少人?
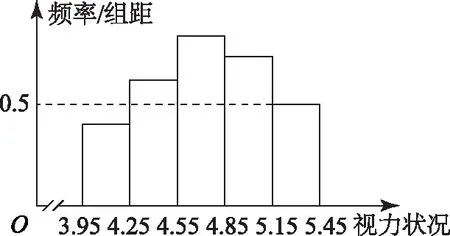
圖1

剖析表面上看本題的回答似乎正確無誤,其實答案是錯誤的,其錯因在于沒有看懂所提供的頻率分布直方圖中數據的含義,誤將該頻率分布直方圖中的縱坐標(頻率與組距的比)當成了頻率,從而導致問題的解答出錯.

點睛解答本題時需注意縱坐標為頻率/組距.繪制頻率分布直方圖的注意事項如下:
1)計算極差,需要找出這組數的最大值和最小值,當數據很多時,可選一個數當參照.
2)將一批數據分組,目的是要描述數據分布規律,要根據數據多少來確定分組數目,一般來說,數據越多,組數越多.
3)列頻率分布表時,可通過逐一判斷各個數據落在哪個小組內,以“正”字計數法確定各個小組內數據的個數.
4)畫頻率分布直方圖時,縱坐標表示頻率與組距的比值,一定不能標成頻率.
4 對莖葉圖的畫法規則認識不夠
例4某市對上下班情況作了抽樣調查,在上下班時間各抽測了12輛機動車的車速如下(單位:km·h-1).
上班時間:30,33,18,27,32,40,26,28,21,28,35,20;
下班時間:27,19,32,29,36,29,30,22,25,16,17,30.
用莖葉圖表示以上數據.
錯解機動車行駛速度的莖葉圖,如圖2所示.

上班下班[5]81679876102257953203026[5]04
圖2
剖析莖葉圖需要對于重復出現的數據進行重復記錄.
正解機動車行駛速度的莖葉圖如圖3.

上班下班[6]81679887610225799532030026[6]04
圖3
點睛畫莖葉圖需要注意將每個數據分為莖和葉兩部分,將表示莖的數字按照由小到大的順序由上到下排列,在寫每行葉子的時候,重復出現的數字也應該按原次數寫入葉子部位,不能只按一次寫入.
5 忽略方差的統計意義
例5甲、乙兩種冬小麥試驗品種連續5年的平均單位面積產量如表1(單位:t·km-2).

表1
若某村要從中引進一種冬小麥大量種植,給出你的建議.
錯解由題意得
甲、乙兩種冬小麥的平均產量都等于10,所以引進兩種冬小麥的任意一種都可以.
剖析上述錯誤在于只對兩種冬小麥的平均產量做了比較,而忽略了對冬小麥產量穩定性的討論.
正解由題意得

點睛平均數反映的是樣本個體的平均水平,方差和標準差則反映了樣本的離散程度.對于形如“誰發揮更好、誰更穩定、誰更優秀”之類的問題,除比較數據的平均值外,還應該比較方差或標準差的大小,以作出更為公正、合理的判斷.
6 弄錯回歸方程中的位置
例6某班5名學生的數學和物理成績如表2.

表2
(1)畫出散點圖;
(2)求物理成績y對數學成績x的線性回歸方程.
錯解(1)散點圖如圖4所示.

圖4
(2)計算得
66×64+63×61=25 054,
732+662+632=27 174,
所以


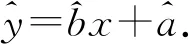

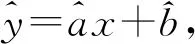
7 忽略求回歸方程的前提——線性相關
例7假設某設備的使用年限和所支出的維修費用如表3中統計資料所示.

表3
能否用線性回歸模型描述兩個變量間的關系?

剖析沒有先判斷兩個變量是否具有線性相關關系.
正解畫出散點圖,如圖5所示,

圖5
從散點圖上看,這些點的分布幾乎沒有什么規律,故不能用線性回歸模型描述兩個變量之間的關系.

8 沒有準確掌握公式中參數的含義
例8有甲、乙兩個班級進行一門考試,將學生考試成績按照優秀和不優秀統計后,得到列聯表(如表4).

表4 班級與成績列聯表
試問能有多大把握認為“成績與所在班級有關系”?
參考公式及數據:
其中n=a+b+c+d.

表5
錯解計算得K2的觀測值為
因為56.86>6.635,所以有99%的把握認為“成績與所在班級有關系”.
剖析由于對2×2列聯表中a,b,c,d的位置不清楚,所以在代入公式時代錯了數值,導致計算結果錯誤.
正解計算得K2的觀測值為
因為0.653<3.841,所以沒有充分證據認為“成績與所在班級有關系”.
點睛獨立性檢驗中,參數K2的公式復雜,計算量大,要弄清公式的特點,熟記公式,避免因粗心而出現錯誤.
鏈接練習
已知數據x1,x2,x3,…,xn是上海普通職工n(n≥3,n∈N*)個人的年收入,設這n個數據的中位數為x,平均數為y,方差為z,如果再加上世界首富的年收入xn+1,則這n+1個數據中,下列說法正確的是( ).
A. 年收入平均數大大增大,中位數一定變大,方差可能不變
B. 年收入平均數大大增大,中位數可能不變,方差變大
C. 年收入平均數大大增大,中位數可能不變,方差也不變
D. 年收入平均數大大增大,中位數可能不變,方差可能不變
鏈接練習參考答案
B.

