主慣導速度誤差短周期波動對子慣導傳遞對準影響分析

楊靖寶，鄧芳瑾，楊松普，王 琳

（1.中國人民解放軍91404部隊，秦皇島066001；2.天津航海儀器研究所，天津300131）

0 引言

隨著海軍慣性裝備的大量改換裝，艦艇逐漸列裝旋轉調制式激光陀螺慣性導航系統。艦艇作為武器作戰平臺，除了要完成自身的導航定位，還需要給艦載武器系統提供姿態、速度和位置基準，供武器系統進行對準。主慣導輸出導航信息精度及穩定性，子慣導的慣性元件精度和傳遞對準方法是影響傳遞對準精度的主要因素。國外關于傳遞對準技術的研究開始較早，目前已趨于成熟。Kain等[1]在傳統速度匹配方法的基礎上加以改進，首次提出了 “速度+姿態”的匹配方法，將傳遞對準的時間縮短至10s以內，同時保證了1mrad以內的姿態精度。Wendel等[2]在將主慣導、子慣導姿態矩陣的乘積作為姿態匹配量的基礎上，右乘主慣導、子慣導之間的方向余弦矩陣（預估值），該方法被稱為最優姿態匹配法。國內各大高校對傳遞對準技術的研究主要集中在對準改進方案的設計、干擾下傳遞對準最優濾波器、傳遞對準中桿臂效應誤差、傳遞對準設計的可觀測性等方面。陳凱等[3]對姿態角匹配、姿態匹配、姿態矩陣匹配和最優姿態匹配4種姿態匹配量之間的相互關系進行了研究，并證明了其統一性。

“速度+姿態”的匹配對準方法即利用姿態信息進行粗對準，利用速度信息進行精對準，是目前艦載武器系統普遍使用的一種傳遞對準方法。“速度+姿態”對準方法對主慣導的速度誤差有兩個方面的要求:一是速度信息精度；二是速度誤差穩定性。雖然旋轉調制式激光陀螺慣性導航系統具有定位精度高的優點，但其在旋轉的同時會造成其姿態、速度和位置具有較大的短周期波動誤差[4-11]，在滿足艦載武器系統短時間傳遞對準方面有著原理性的缺陷。劉為任等[12]提出了一種基于不同旋轉控制策略的雙慣導數據融合方法，估計并補償了主慣導慣性元件的誤差，從而減小了主慣導速度誤差的波動幅度。

本文基于子慣導對準時間短（對準時間小于10min）的特點，對旋轉調制式激光陀螺慣性導航系統速度誤差的短期特性對子慣導對準精度的影響建立了數學模型，提出了主慣導速度誤差的一次項系數與子慣導初始對準水平姿態誤差呈線性關系，主慣導速度誤差的二次項系數與子慣導初始對準航向誤差呈線性關系，并通過仿真及實驗對其進行了驗證。該實驗結果定量地說明了速度誤差短周期波動對子慣導短時間對準航向誤差及水平姿態誤差的影響，在制定旋轉控制策略、設計傳遞對準方案時有較大的參考價值。

1 速度誤差短周期波動對子慣導短時間對準影響模型

1.1 東向速度誤差對子慣導短時間對準影響

當子慣導對準時間小于10min時，將速度誤差相對時間的模型建立為二次項方程，東向速度誤差的表達式如下

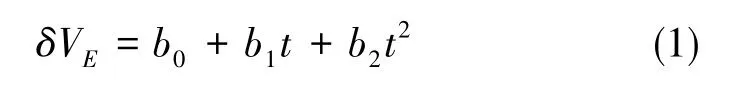
式（1）中，δVE為東向速度誤差，t為時間。

對準過程中，東向速度誤差模型如下[13-14]

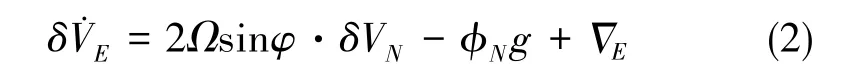
式（2）中，Ω為地球自轉角速度，φ為緯度，δVN為北向速度誤差，φN為橫搖角，g為地球重力矢量，為東向加速度計零位。

橫搖角誤差模型如下[13-14]

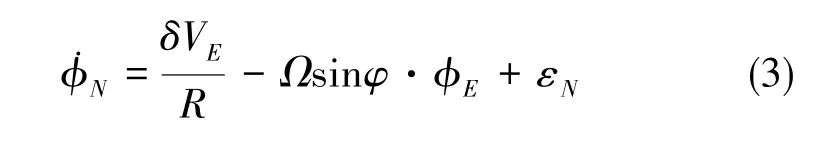
式（3）中，R為地球半徑，φE為縱搖角，εN為北向陀螺零偏。

由于地球自轉角速度Ω約為7×10－5rad/s，傳遞對準過程中速度誤差約為0.1m/s～0.2m/s，緯度的正弦值sinφ也要小于1.0，三者的乘積要小于1×10－5， 與加速度計零位的 10－4量級相比可以忽略不計，因此可將式（2）簡化為

通過式（9）可以看出，在子慣導初始對準過程中，東向速度的一次項波動相當于在子慣導中引入了等效東向加速度計零位。根據慣性導航系統初始對準穩態誤差值可知，子慣導初始對準橫搖角度誤差穩態值βs與東向速度的一次項系數的量值關系如式（11）[13-14]所示，橫搖角一次微分與北向陀螺相等，不影響初始對準結果。因此，可以不考慮東向速度的二次項系數。

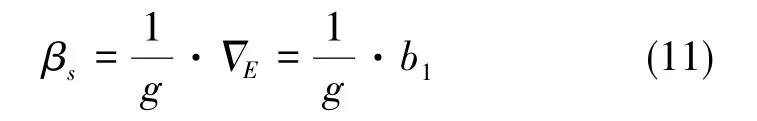
1.2 北向速度誤差對子慣導短時間對準影響

同樣地，北向速度誤差相對時間的模型建立為二次項方程，北向速度誤差表達式為

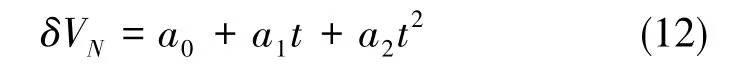
對準過程中，北向速度誤差為

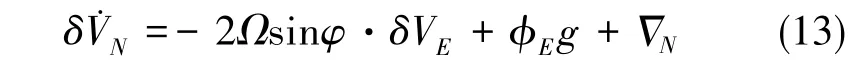
式（13）中，為北向加速度計零位。

縱搖角誤差模型為

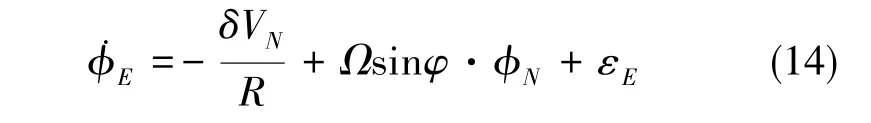
式（14）中，εE為東向陀螺零偏。

與對式（2）和式（3）的分析方式相同， 式（13）和式（14）可以簡化為

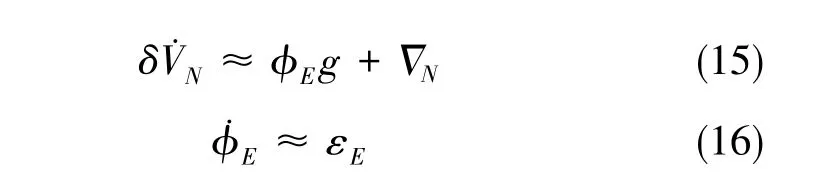
通過對式（12）分別求一次導和二次導，得到

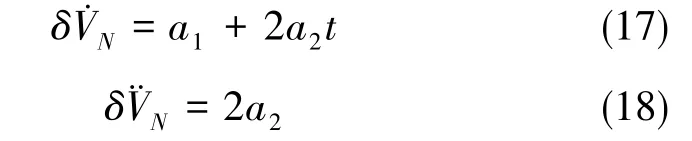
對式（15）相對時間求一次導，有

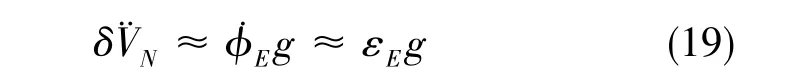
對比式（15）和式（17）， 有

由式（20）可知，北向速度的一次項波動與北向加速度計零位相等。根據慣性導航系統初始對準穩態分析可知，北向速度一次項影響子慣導縱搖角對準誤差穩態值αs， 量值關系如下[13-14]

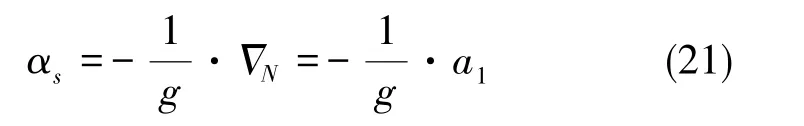
對比式（18）和式（19）， 有

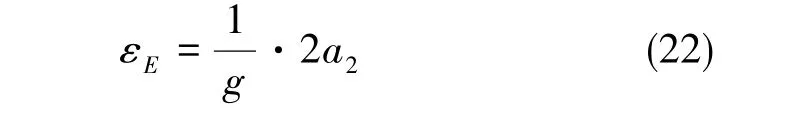
由式（22）可知，北向加速度計二次項波動與等效東向陀螺零偏正相關。根據慣性導航系統初始對準穩態分析可知，由北向速度二次項波動引起的子慣導初始對準航向誤差穩態值γs的表達式為

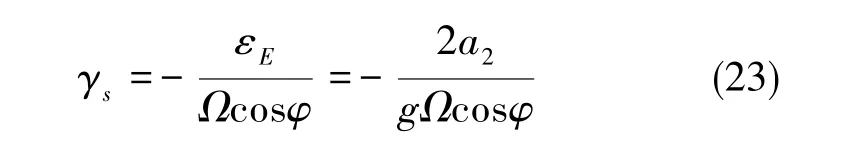
2 數字仿真分析

在航向90°、 經度117.1446°、 緯度39.1818°、不設定子慣導陀螺和加速度計誤差的情況下，通過Matlab模擬對生成雙軸系統（主慣導）和純捷聯系統（子慣導）的數據進行純數字仿真，對上述定量分析過程進行驗證，將子慣導對準時間設為8min。

2.1 北向速度二次項系數仿真

假設誤差源只有速度誤差二次項、其他各項為0，當a2取不同值時，仿真得到的航向誤差如表1和圖1所示，同時將設定的二次項波動系數、緯度值代入式（23），將得到的理論值列入表1。通過表1的仿真值與理論值對比可以看出，所推導的二次項波動系數與子慣導對準航向精度基本一致， 式（23）是成立的。

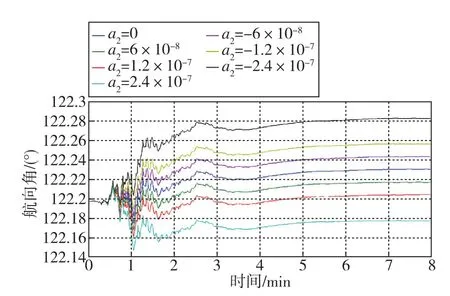
圖1 a2取不同值時的航向誤差曲線Fig.1 Heading error curves when a2takes different values

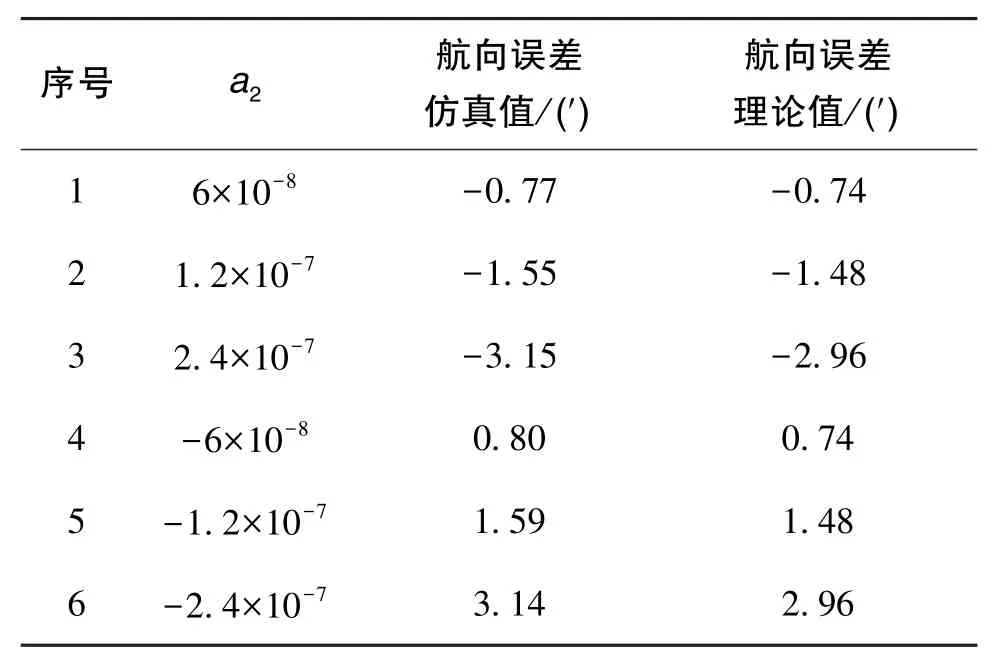
表1 a2與航向誤差的關系Table 1 Relationship between a2and heading error

數字仿真結果表明，主慣導速度誤差的二次項系數a2與子慣導初始對準航向誤差呈線性關系。

2.2 北向速度一次項系數仿真

假設誤差源只有速度誤差一次項、其他各項為0，當a1取不同值時，仿真得到的縱搖誤差如表2和圖2所示，同時將設定的一次項波動系數代入式（21），將得到的理論值列入表2。通過表2的仿真值與理論值對比可以看出，所推導的一次項波動系數與子慣導對準縱搖角精度基本一致，式（21）是成立的。

圖2 a1取不同值時的縱搖誤差曲線Fig.2 Pitch error curves when a1takes different values

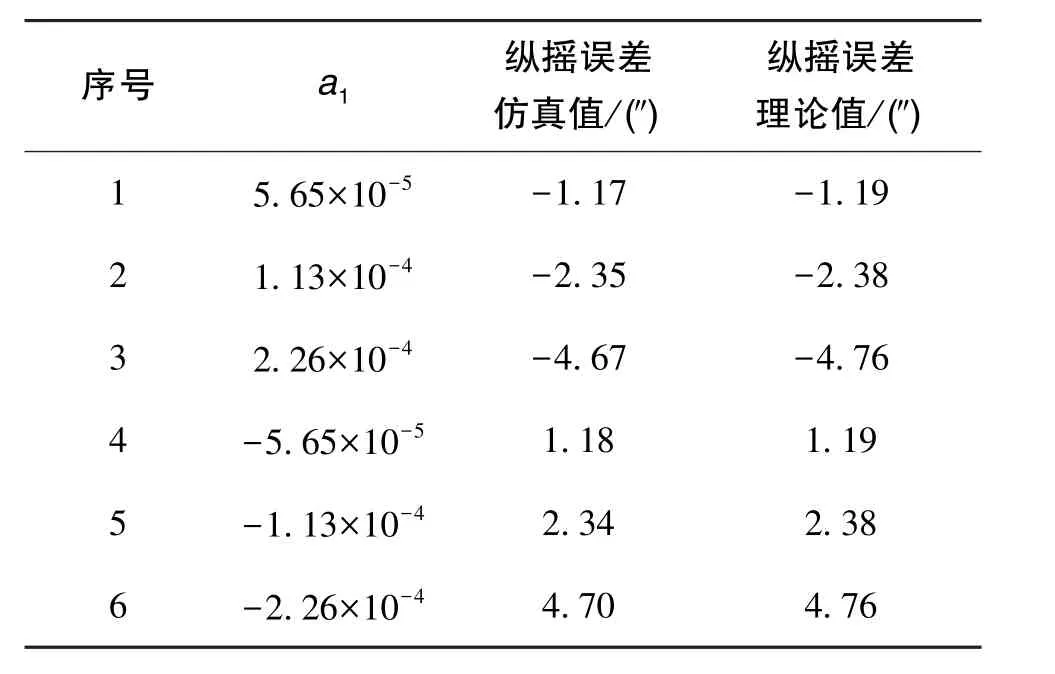
表2 a1與縱搖誤差的關系Table 2 Relationship between a1and pitch error

數字仿真結果表明，主慣導速度誤差的一次項系數a1與子慣導初始對準水平姿態誤差呈線性關系。

3 半實物實驗

利用雙軸激光慣導和船用光纖捷聯慣導的靜態實測數據進行了60次的8min傳遞對準（1min粗對準，7min精對準）仿真實驗，對數字仿真的結論進行驗證，實驗數據如表3、表4所示。

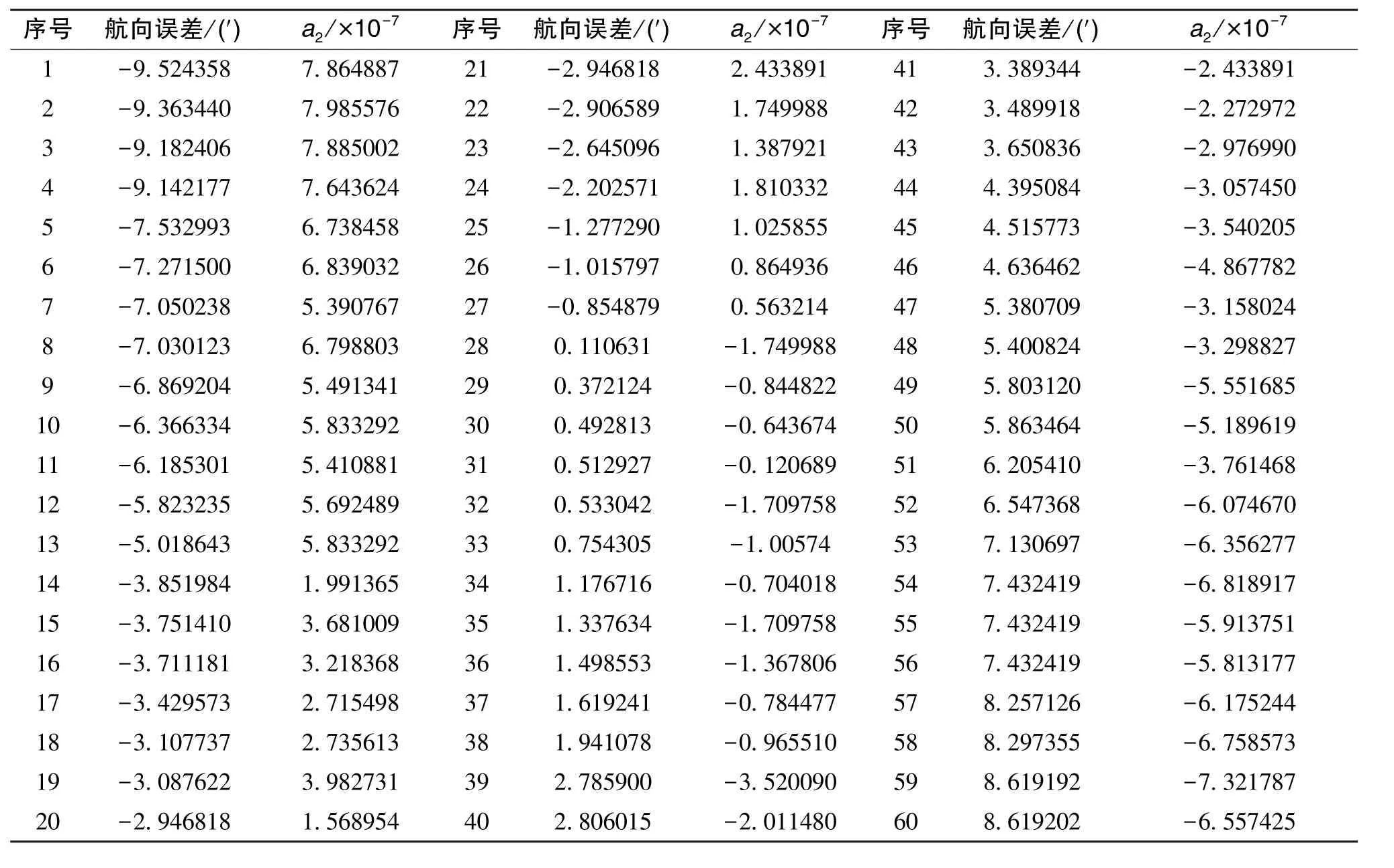
表3 a2與航向誤差關系（60個樣本）Table 3 Relationship between a2and heading error （60 samples）

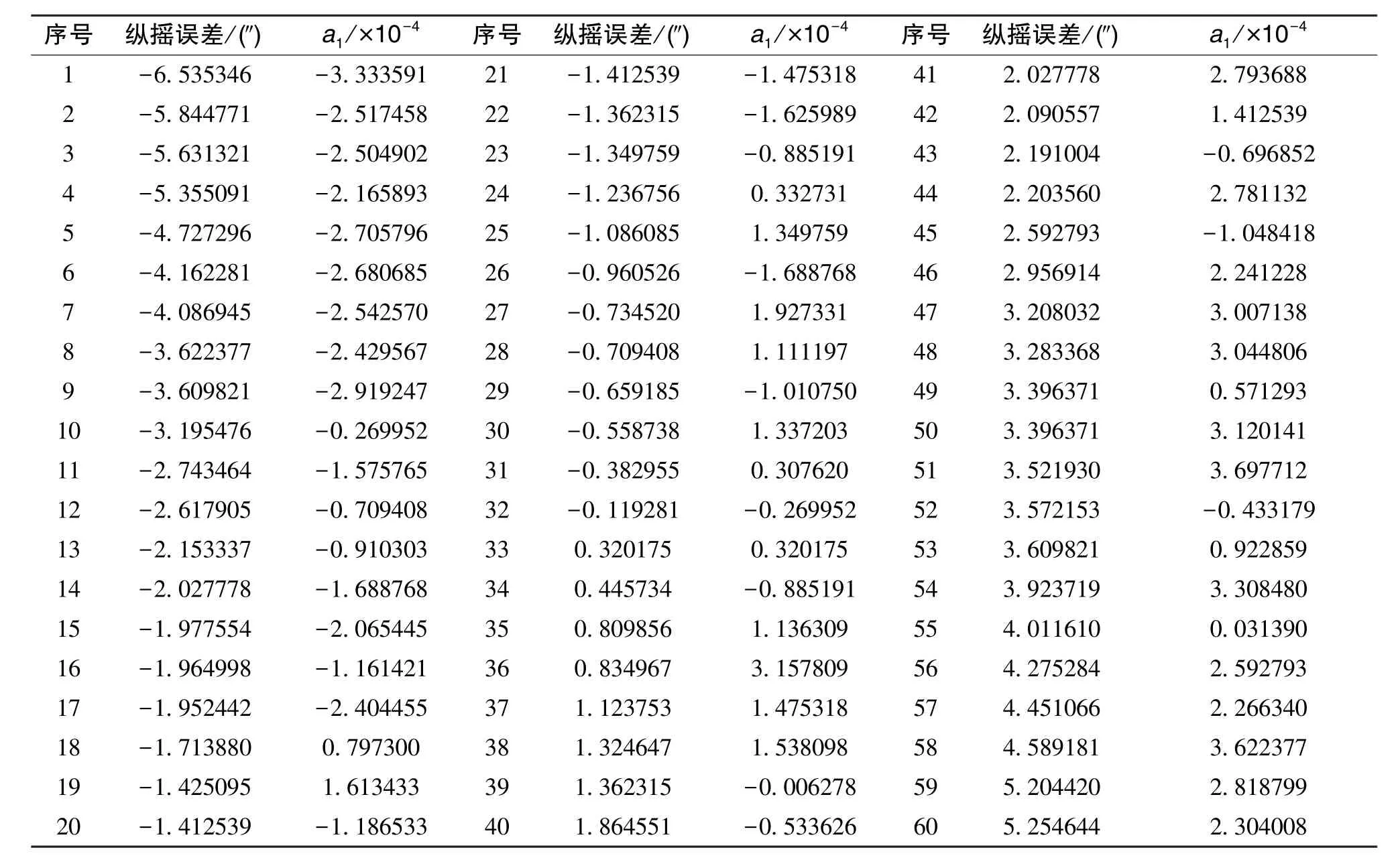
表4 a1與縱搖誤差關系（60個樣本）Table 4 Relationship between a1and pitch error （60 samples）

對60次對準過程中的主慣導北向速度誤差分別進行二次項擬合，二次項系數a2與對準結束時刻航向誤差的關系如圖3所示，一次項系數a1與對準結束時刻縱搖誤差的關系如圖4所示。

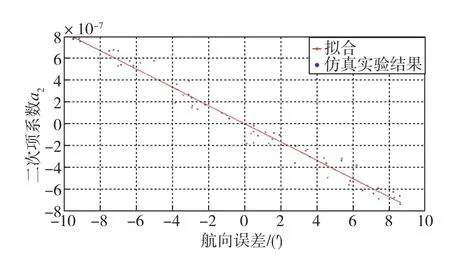
圖3 a2與航向誤差關系（60個樣本與擬合直線）Fig.3 Relationship between a2and heading error（60 samples and the fitting line）

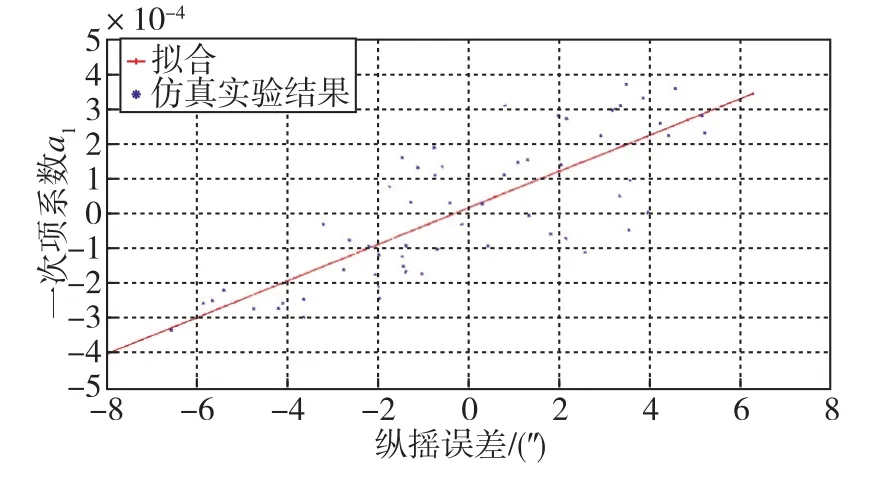
圖4 a1與縱搖誤差關系（60個樣本與擬合直線）Fig.4 Relationship between a1and pitch error（60 samples and the fitting line）

對各點進行線性擬合，由擬合曲線可以看出，二次項系數與子慣導航向對準結果基本呈線性關系，一次項系數與子慣導縱搖對準結果基本呈線性關系， 式（21）和式（23）的結論是正確的。

4 結論

本文理論推導了主慣導速度誤差一次項波動和二次項波動對子慣導初始對準水平姿態誤差和航向誤差的影響，給出了量化關系。在傳遞對準過程中，主慣導速度誤差的一次項系數與子慣導初始對準水平姿態誤差呈線性關系，主慣導速度誤差的二次項系數與子慣導初始對準的航向誤差呈線性關系，數字仿真和半實物仿真證明了推導的正確性。