GPS移動基準站差分定位算法

周金龍，孫永榮，吳 玲，曾慶化

（南京航空航天大學自動化學院導航研究中心，南京211106）

0 引言

相對定位指的是利用兩臺或以上GPS接收機同步觀測相同衛星，以確定基線在協議坐標系中的相對位置和基線向量[1]。傳統相對定位建立在基準站固定（即基準站精確位置已知）的基礎上，移動站在通過數據鏈獲得基準站的差分數據后，進行動態差分定位。但是，該定位模式受限于基準站位置固定、通信覆蓋范圍有限等問題[2]，這些問題使其在空中加油、飛機編隊飛行等特殊場合中難以適用。為此，本文針對移動基準站差分定位開展了研究。

喻國榮[3]針對動對動定位過程中整周模糊度求解及周跳探測與修復這兩個核心問題展開了相關研究，討論了動對動定位中的模糊度搜索準則與檢驗方法，并提出了一種模糊度雙空間搜索算法，實現了厘米級定位精度。王智等[4]在Buist[5]研究的基礎上，提出了一種艦船三天線動對動定位模型，并最終獲得了厘米級定位結果。Lachapelle等[6]通過多天線約束來提升整周模糊度搜索效率。目前，研究最為成熟的動對動相對定位技術是美國的海基聯合精密進近與著陸系統（Sea Based Joint Precision Approach and Landing System， SB-JPALS）[7]。

本文利用載波相位和偽距觀測值的雙差組合求解測站間精確的相對位置，以此來大幅度消除觀測值之間的空間相關誤差，削弱衛星鐘差、接收機鐘差、電離層延遲誤差和對流層延遲誤差[8-9]，從而獲得高精度的相對定位結果。最后，利用接收機采集到的導航原始數據進行實測數據驗證。分析結果表明:本文所采用的GPS無固定基準站差分定位算法可達到厘米級的動對動相對定位精度。

1 無固定基準站差分定位算法

1.1 單差/雙差觀測方程

差分相對定位主要采用偽距和載波相位觀測值，其不同測站間的單差觀測方程如下

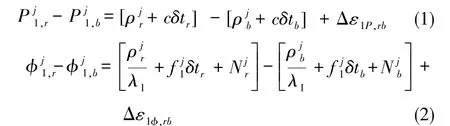
在式（1）、 式（2）中，c為光速；分別為移動站、基準站接收載波L1關于衛星j的偽距觀測值；分別為移動站、基準站接收載波L1關于j衛星的載波相位觀測值；分別為移動站、基準站的位置與衛星之間的幾何距離；δtr、δtb分別為移動站接收機、基準站接收機的鐘差；λ1為載波L1的波長；為載波L1的頻率；分別為基準站、移動站關于衛星j的整周模糊度； Δε1P，rb為偽距單差測量噪聲； Δε1φ，rb為載波相位單差測量噪聲。

將式（1）和式（2）進行偽距/載波相位組合，可得

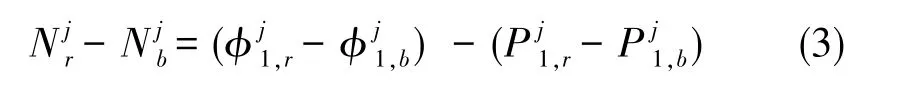
進而可以獲得單差模糊度浮點解。

通過以上單差觀測方程，可以進一步構建雙差觀測方程。兩顆衛星信號頻率相同，則雙差觀測方程的最終形式為

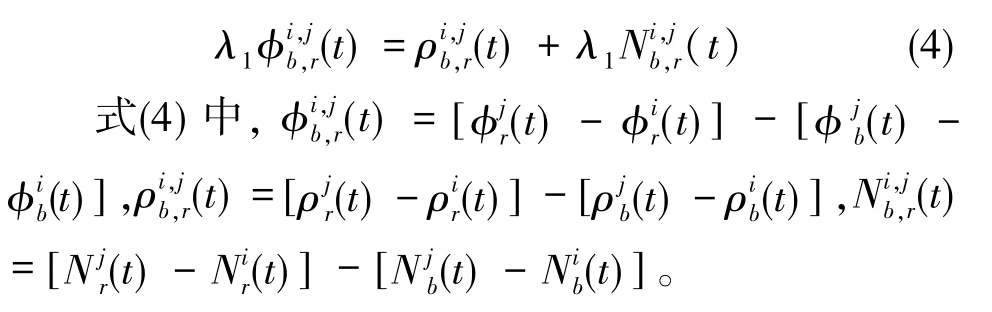
1.2 擴展Kalman濾波

雙差觀測模型構建后，由于其數學模型為非線性方程組，故需要采用擴展Kalman濾波（EKF）進行參數估計。通過EKF處理后，可獲得精確模糊度浮點解與測站坐標。

EKF模型方程為

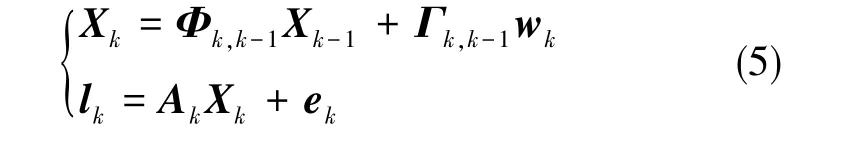
在式（5）中，wk為系統誤差向量，ek為觀測誤差向量，wk～N（0，Σwk），ek～N（0，Rk）。

實例中， 令X＝Φk，k－1Xk－1，HT＝Ak，v1＝lk－AkX，Γk，k－1為單位陣。其中，H為雙差觀測方程系數矩陣，Σk為雙差觀測方程狀態向量X的協方差矩陣，Rk為載波相位-偽距測量誤差的協方差矩陣，則有

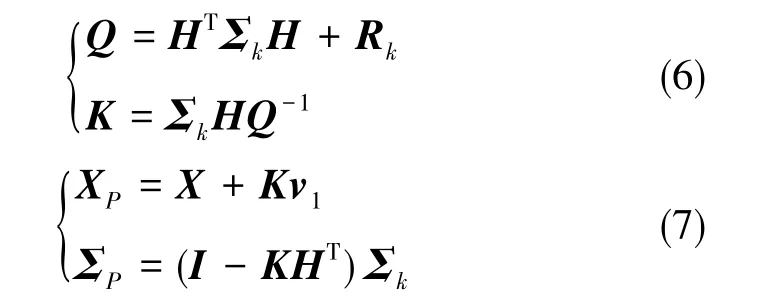
式（7）中，XP為浮點解，ΣP為狀態向量的協方差矩陣。

1.3 整周模糊度求解

高精度相對定位的關鍵是解決載波相位觀測量中的整周模糊度問題[10-11]。在獲得精確浮點解XP及其協方差矩陣ΣP后，采用LAMBDA算法進行整周模糊度固定，以解出精確定位結果。

由于在實際數據中，浮點解與其協方差矩陣的相關性較大，這帶來了整周模糊度搜索空間狹長、效率低下等問題[12]。因此，在進行模糊度固定前，需要進行模糊度去相關轉換。對經Kalman濾波后的結果進行變換，可得

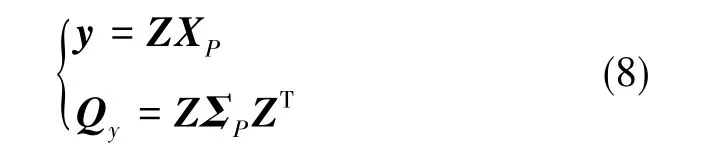
式（8）中，Qy為狀態向量y的協方差矩陣。再對Qy做變換得Qb、Qab，b為狀態向量中模糊度浮點解，Qb為狀態向量中模糊度的協方差矩陣，Qab為狀態向量中坐標參數與模糊度的協方差矩陣。

對Qb進行Cholosky分解[13]，即

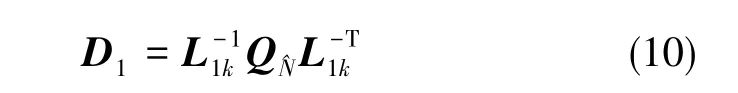
再對D1做Cholosky分解，將分解的單位下三角矩陣取整，用L2k表示，再做變換有

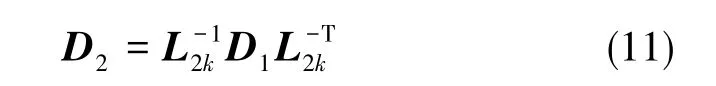
如此循環，直至分解的單位下三角矩陣取整后為單位陣，故有

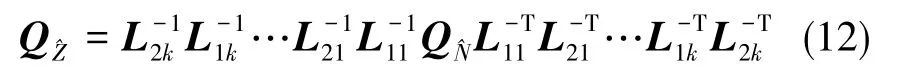
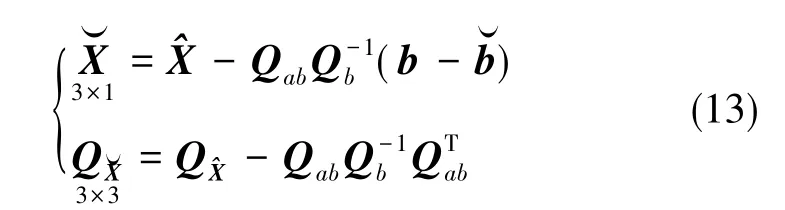
2 實驗結果及分析

本文采用實驗驗證法來分析所研究算法的正確性及有效性。2018年11月17日14點30分，在南京航空航天大學將軍路校區東部操場，分別進行了靜態相對定位、固定基準站和移動基準站差分定位實驗，并采集了相關原始數據。

本實驗采用Novatel OEM-615板卡衛星導航授時接收機來采集星歷/觀測數據，OEM-615是Novatel公司推出的第六代產品中尺寸最小的多系統板卡，支持GPS、GLONASS、Galileo和BDS四系統多頻信號。

接收機的實物連接如下:圖1（a）為基線長度固定的實驗儀器連接示意圖，按差分定位要求連接好儀器后，推動小車即可進行固定基線動態相對定位實驗數據的采集；圖1（b）為基線長度變化的實驗儀器連接示意圖，按要求連接完畢后，移動小車即可進行變基線長度相對定位實驗數據的采集。

圖1 實驗儀器Fig.1 Laboratory apparatus

2.1 靜態相對定位

固定基線的長度為8.41m，根據所收集的原始數據進行計算后，繪制偽距及載波相位殘差圖分別如圖2（a）、 圖2（b）所示。 通過觀測數據殘差圖可以發現:無論是偽距殘差還是載波相位殘差，其數值均在 “0”附近變化，這說明觀測數據質量較好。其中，部分時刻偽距殘差值較大，這表明存在延遲項使得偽距變長，如多徑問題、對流層延遲等；在其他大部分時刻，偽距觀測值和載波相位觀測值殘差均較小，數值在 “0”附近抖動，這表明存在一定的噪聲干擾。

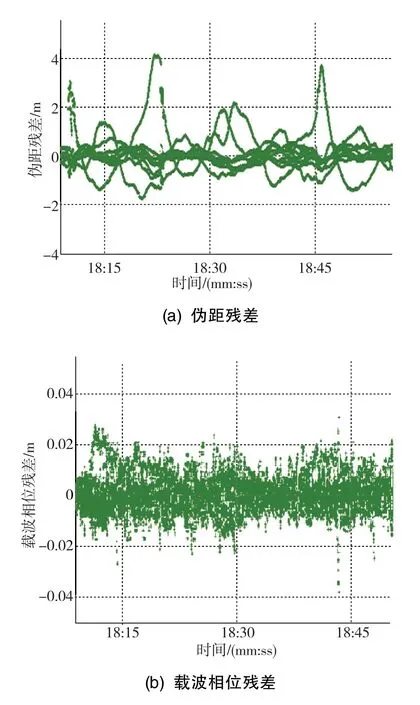
圖2 偽距殘差及載波相位殘差圖Fig.2 Diagram of pseudo range residual and carrier phase residual

根據收集到的數據，通過靜態相對定位模式，解算得到基線長及各向標準差，如圖3所示。

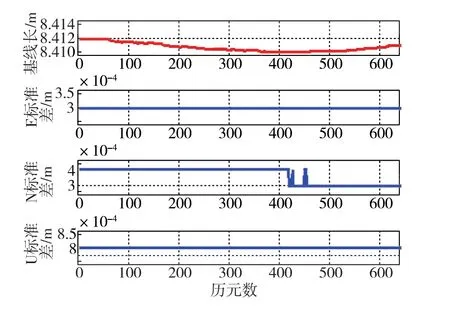
圖3 定位結果及各向標準差Fig.3 Diagram of positioning results and standard deviation in all directions

通過以上結果分析，得到該定位模式下靜態相對定位E、N、U三個方向的標準差均值分別為3.00×10－4m、 3.66×10－4m、 8.00×10－4m， 這表明定位結果可靠且精度較高。

2.2 固定基準站差分相對定位

在該定位模式下，將基準站固定在一個已知的坐標點，然后利用基準站的坐標修正信息對移動站的定位結果進行修正，以獲得更為精確的坐標值。將一臺接收機固定在操場上一點，然后推著小車（移動站安放在小車上）移動，以此來獲得固定基準站差分相對定位實驗數據。通過算法解算得到基線長及各向標準差，如圖4所示。

圖4 定位結果及各向標準差Fig.4 Diagram of positioning results and standard deviation in all directions

通過以上結果分析，得到該定位模式下E、N、U三個方向的標準差均值分別為4.6×10－3m、5.2×10－3m、 1.09×10－2m， 實現了厘米級動態差分定位。

2.3 基線長度固定的移動基準站差分相對定位

在該定位模式下，固定基線的長度為0.73m，實驗裝置如圖1（a）所示。在設置相應的指令后，推著小車沿著操場跑道最外圈進行數據采集。根據定位結果繪制移動站相對基準站基線長度變化曲線，如圖5所示。在圖5中，坐標原點即為基準站。可以看出，實驗結果與實際運動情況一致。

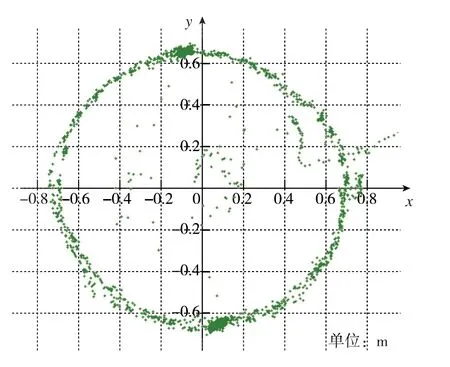
圖5 移動站相對基準站的移動軌跡Fig.5 Moving track of the mobile station relative to the reference station

通過對圖6進行分析，在基線長度固定的移動基準站相對定位情況下，其E、N、U三個方向的標準差均值分別為 6.7×10－3m、 8.2×10－3m、1.95×10－2m。

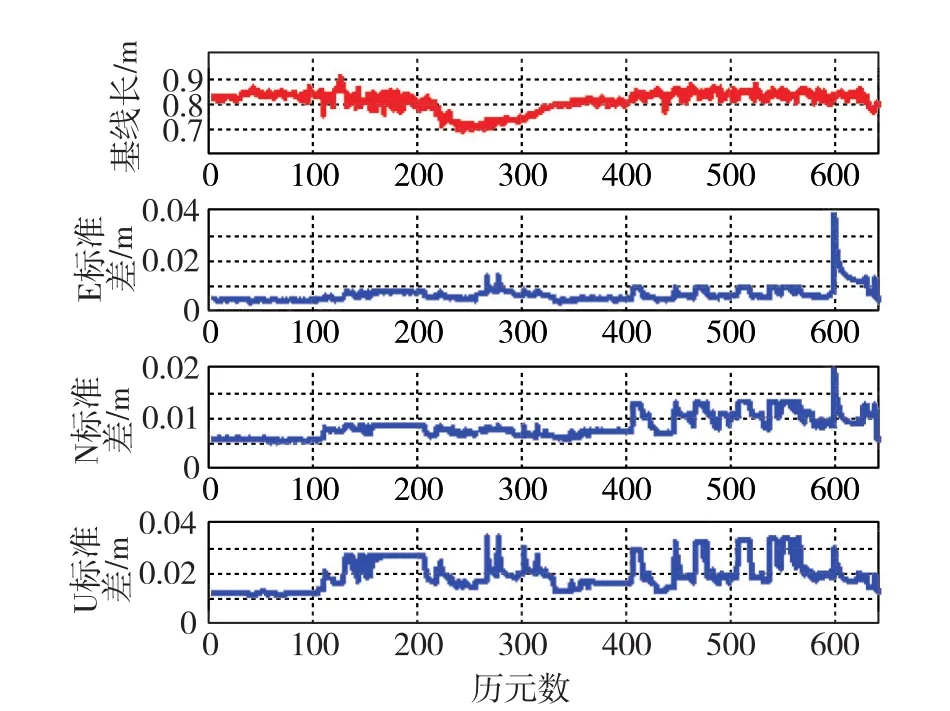
圖6 定位結果及各向標準差Fig.6 Diagram of positioning results and standard deviation in all directions

2.4 基線長度不固定的移動基準站差分定位

在該定位模式下，實驗裝置如圖1（b）所示，實驗路線如圖7所示。在進行數據采集時，基準站按圖7中的紅色路線進行移動，移動站按圖7中的藍色路線進行移動。

圖7 測站移動軌跡Fig.7 Moving track of the stations

通過對圖8進行分析，在基線長度不固定的移動基準站差分定位情況下，其E、N、U三個方向的標準差均值分別為 4.8×10－3m、 5.3×10－3m、1.55×10－2m。

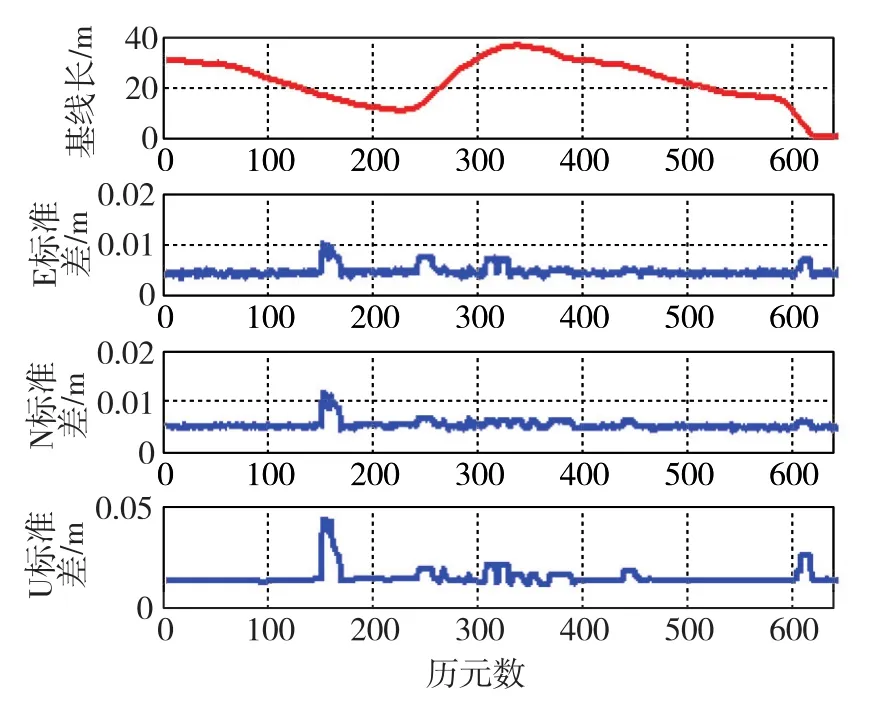
圖8 定位結果及各向標準差Fig.8 Diagram of positioning results and standard deviation in all directions

2.5 實驗結果綜合分析

進一步對以上四種不同情況的定位結果進行分析，可以得到基線均方差，如圖9所示。由圖9可知:靜態相對定位和傳統固定基準站差分定位模式的模糊度比較容易固定，并且解算精度較高；而移動基準站差分定位的模糊度較難固定，但在模糊度固定的情況下，基線均方差普遍保持在2cm左右，并且其隨著觀測數據的增加，逐漸保持穩定。

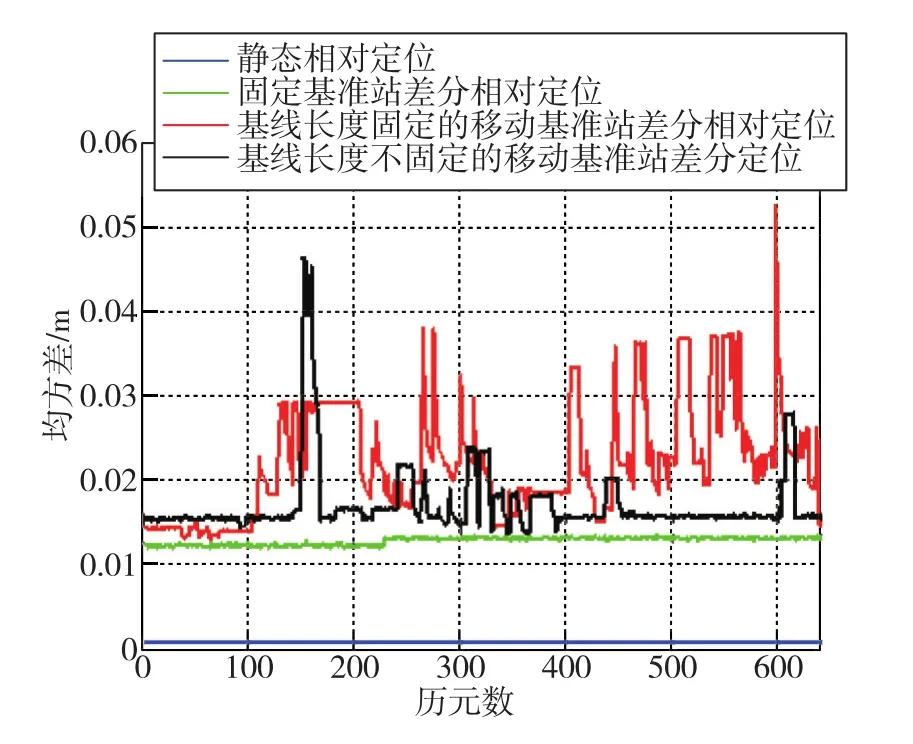
圖9 四種定位方式的基線均方差Fig.9 Baseline standard deviation of four positioning methods

表1為四種定位方式的統計特性，由分析可以得出:靜態相對定位在定位過程中保持模糊度固定，并且基線均方差最小，達到毫米級定位標準；在固定基準站差分定位模式下，模糊度基本保持固定，解算結果質量較好，基線均方差均值保持在1.3cm附近；在移動基準站差分定位模式下，模糊度較難固定，無論是在基線長度固定還是基線長度變化情況下，算法解算的基線均方差最大值均在5cm左右，模糊度固定后保持在2cm附近。

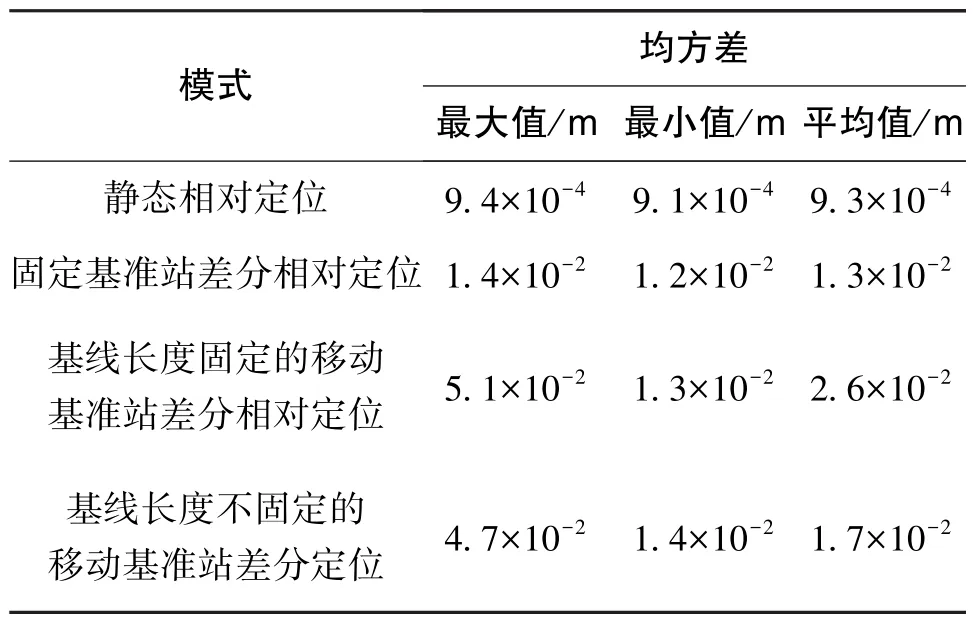
表1 四種定位方式的統計特性Table 1 Statistical characteristic of four positioning methods

3 結論

本文圍繞無人機空中加油中的導航定位技術開展研究工作，針對傳統差分相對定位技術受限于基準站位置固定等情況，展開了移動基準站差分定位技術的研究。在傳統差分定位算法理論基礎上，分析了基準站坐標偏差對移動站解算結果的影響，利用雙差觀測方程構建了移動基準站差分定位數學模型，并通過Kalman濾波和LAMBDA算法進行整周模糊度求解，獲得最終相對定位結果。四種不同定位方式的實驗結果表明，靜態相對定位基線均方差小于1mm，動態基線均方差小于5cm，符合動態相對定位精度要求，從而驗證了本文所研究的無固定基準站差分定位方法的理論與實用價值。