基于角增量和矢量模值觀測的光纖陀螺溫度漂移參數(shù)分段估計(jì)

崔加瑞，吳文啟，何曉峰

（國防科技大學(xué)智能科學(xué)學(xué)院，長沙410073）

0 引言

光纖陀螺捷聯(lián)慣導(dǎo)系統(tǒng)由于具備可靠性高、壽命長、精度高、工藝相對簡單等優(yōu)點(diǎn)，被廣泛應(yīng)用于航空、航天、航海及陸地車輛定位定向等領(lǐng)域，然而其核心部件——光纖陀螺對溫度變化較為敏感，非互易性相移誤差是造成光纖陀螺溫度漂移的主要原因[1]。采用軟件補(bǔ)償溫度漂移的方法可以在不增加硬件成本的條件下提高光纖陀螺的測量精度[1-8]，故其在工程實(shí)踐中得到了廣泛應(yīng)用。由于光纖陀螺在不同溫度段具有不同的溫度特性，分段估計(jì)光纖陀螺溫度漂移能夠更為細(xì)致地描繪溫漂規(guī)律，進(jìn)而更精確地補(bǔ)償誤差[2]。溫度漂移具有較強(qiáng)的非線性特點(diǎn)，大量基于非線性模型的分段溫度漂移估計(jì)方法被提出，主要有:基于多尺度和支持向量機(jī)[3]、RBF神經(jīng)網(wǎng)絡(luò)[4]、自適應(yīng)神經(jīng)網(wǎng)絡(luò)[5]、Elman網(wǎng)絡(luò)[6]、粒子群優(yōu)化算法[7]等。但是總體而言，上述智能算法擬合非線性溫度漂移的方法計(jì)算量大，建立模型耗時(shí)長且網(wǎng)絡(luò)結(jié)構(gòu)設(shè)計(jì)缺乏理論指導(dǎo)，較為依賴數(shù)據(jù)和經(jīng)驗(yàn)，容易產(chǎn)生過擬合問題，進(jìn)而導(dǎo)致模型適用性變差，而基于多項(xiàng)式模型來進(jìn)行溫度漂移估計(jì)是如今工程實(shí)踐中最為有效的方法[8]。文獻(xiàn)[9]使用分段動(dòng)態(tài)測試插值法得到不同溫度下的陀螺溫度漂移零偏，但是和其他陀螺標(biāo)定技術(shù)一樣，該方法對陀螺零偏的估計(jì)依賴高精度轉(zhuǎn)臺(tái)或慣導(dǎo)系統(tǒng)多位置自對準(zhǔn)過程[10-14]。然而，針對在分段溫度漂移估計(jì)過程中產(chǎn)生的陀螺溫度漂移值在分段區(qū)間交接點(diǎn)的不連續(xù)性問題 （即參數(shù)的邊界條件問題），上述分段補(bǔ)償算法均未進(jìn)行說明。

針對光纖陀螺在不同溫度段之間由溫漂參數(shù)不同導(dǎo)致的誤差不連續(xù)問題，本文提出了一種基于角增量和矢量模值觀測的光纖陀螺溫度漂移參數(shù)分段最小二乘估計(jì)方法。使用低階溫度漂移模型即可實(shí)現(xiàn)光纖陀螺捷聯(lián)慣導(dǎo)系統(tǒng)中三軸角增量光纖陀螺的溫度漂移補(bǔ)償，同時(shí)推導(dǎo)了各溫度段零偏與光纖陀螺溫漂參數(shù)的關(guān)系，給出了相應(yīng)的邊界條件。通過地球自轉(zhuǎn)角速度模值觀測法得到了第一段溫度區(qū)間的零偏后，可以得出其他溫度段的零偏，保證了光纖陀螺輸出在各溫度段的連續(xù)性。通過溫控轉(zhuǎn)臺(tái)升溫實(shí)驗(yàn)，驗(yàn)證了本文提出方法的有效性，本文方法的補(bǔ)償效果優(yōu)于傳統(tǒng)整段最小二乘估計(jì)方法。

1 溫度漂移分段模型與邊界條件

由于采用了分段估計(jì)，各段內(nèi)僅需考慮一階模型，建立的光纖陀螺溫度漂移模型如下

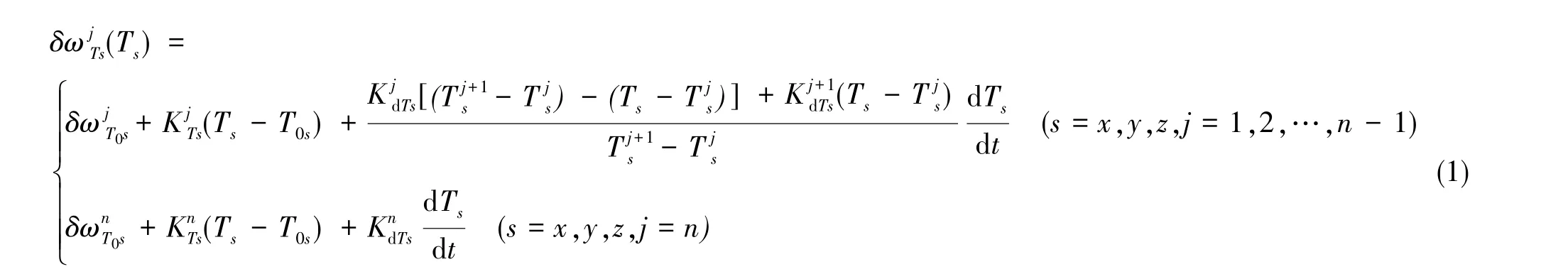
式（1）中，假設(shè)溫度分為n段，上標(biāo)j表示第j段溫度區(qū)間，為IMU中陀螺s的光纖環(huán)測量溫度，T0s為基準(zhǔn)點(diǎn)溫度。為簡便起見，可以令，即T0s為第一段溫度區(qū)間的起始溫度，為第j溫度段的溫漂系數(shù)，為第j段溫度區(qū)間內(nèi)的等效陀螺零偏，由此得到的分段溫度漂移曲線如圖1所示。

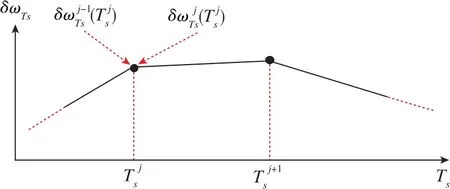
圖1 光纖陀螺分段溫度漂移曲線Fig.1 Curve of FOG segment thermal drift

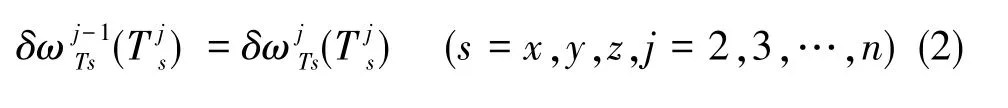
由圖1可知，分段溫度漂移估計(jì)需要滿足在交接點(diǎn)的邊界條件，必須使前后兩段溫度漂移模型計(jì)算的漂移值相同，即具有相同的零偏。各溫度段零偏邊界條件為

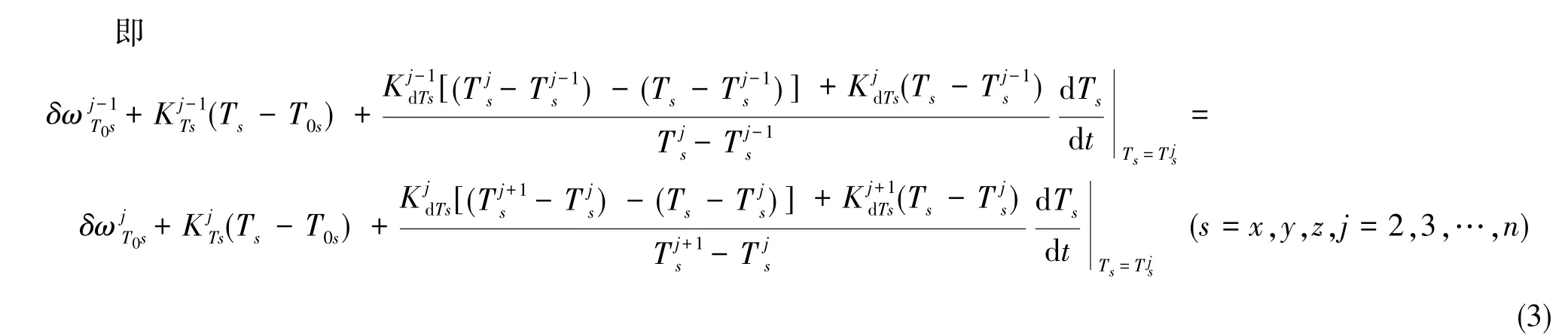
當(dāng)溫度梯度不同 （即溫度變化速率不同）時(shí)，也可以保證零偏的差值相同，即保證了對于不同溫度變化情況零偏值的一致性，這有利于在工程實(shí)踐中進(jìn)行補(bǔ)償。

2 光纖陀螺誤差參數(shù)估計(jì)

2.1 基于角增量的最小二乘溫度漂移分段估計(jì)方法

考慮邊界條件，將各溫度段的零偏通過第一個(gè)溫度段的零偏表示，式（1）可改寫為

本文慣導(dǎo)系統(tǒng)的光纖陀螺為角增量陀螺，將一段時(shí)間 （tj，m+1，tj，m）內(nèi)的陀螺角增量輸出進(jìn)行累加，能夠得到包含溫度漂移的角速率積分增量，將其除以積分時(shí)間可以得到等效陀螺角速率輸出，如下所示

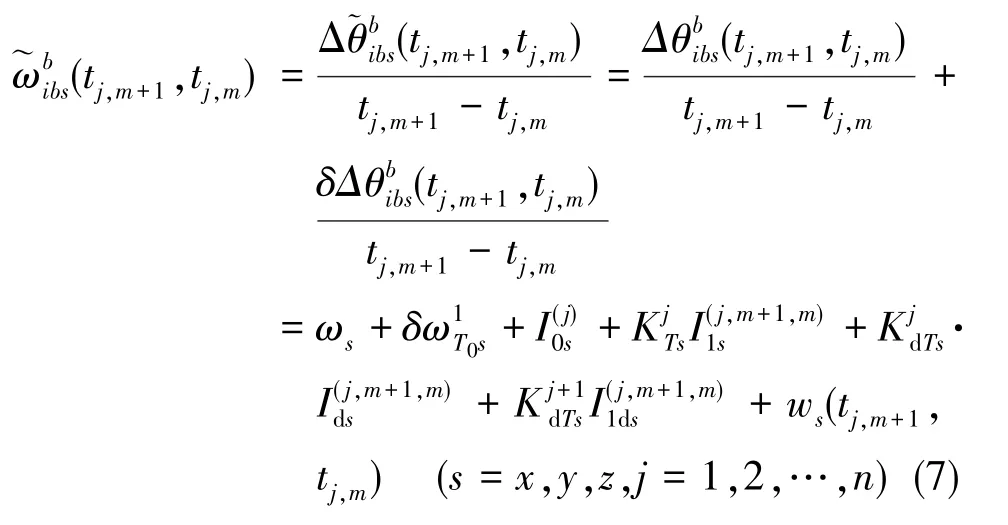
式（9）中，各符號(hào)含義如下

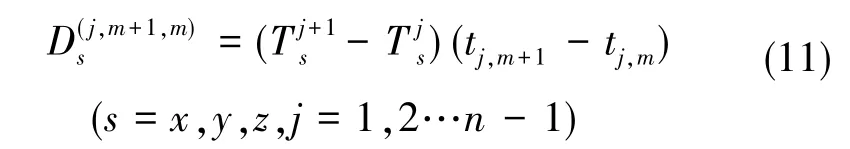
式（10）中，Mj為第j個(gè)溫度段的積分時(shí)間段數(shù)量，方程組數(shù)量大于2n+1，即可通過最小二乘法求得除常值零偏以外的各個(gè)軸向陀螺溫度模型的2n個(gè)參數(shù)，至此解決了各溫度區(qū)間溫度漂移的連續(xù)性問題。接下來，將使用基于地球自轉(zhuǎn)角速度矢量模值的零偏估計(jì)方法對第一段溫度區(qū)間的常值零偏進(jìn)行估計(jì)，即可得到全溫度段連續(xù)的溫度漂移模型。

2.2 基于地球自轉(zhuǎn)角速度模值的零偏估計(jì)補(bǔ)償方法

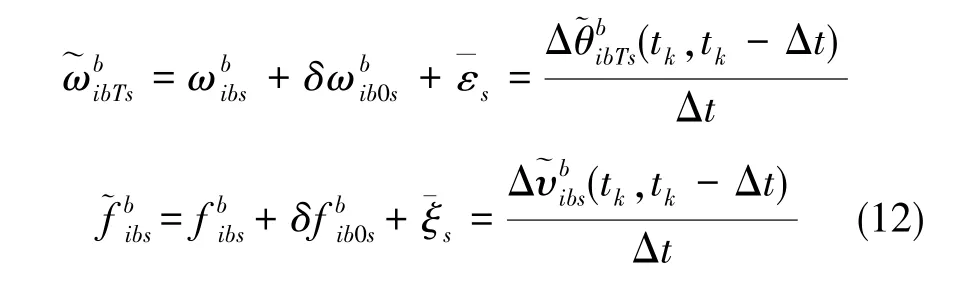
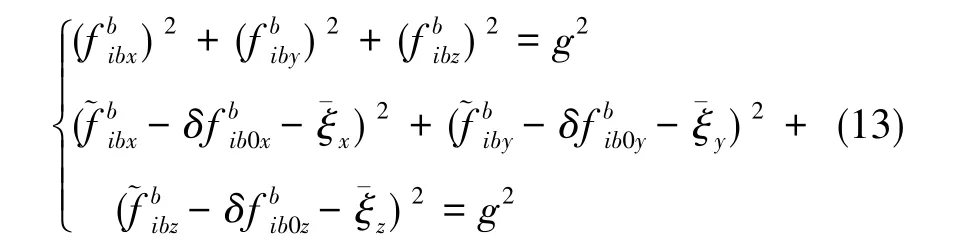
認(rèn)為零偏的平方項(xiàng)和噪聲相關(guān)項(xiàng)遠(yuǎn)小于其他項(xiàng)，忽略高階小量，旋轉(zhuǎn)IMU改變陀螺、加速度計(jì)的敏感軸方向，得到不同的測量結(jié)果，可得

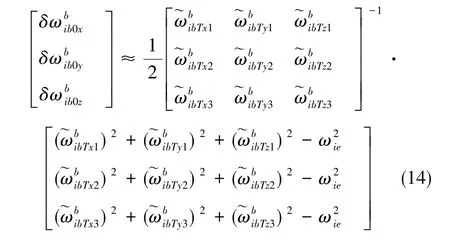
依次使x、y、z陀螺敏感軸與地球自轉(zhuǎn)角速度矢量方向大致一致，可使陀螺零偏估計(jì)結(jié)果最優(yōu)。

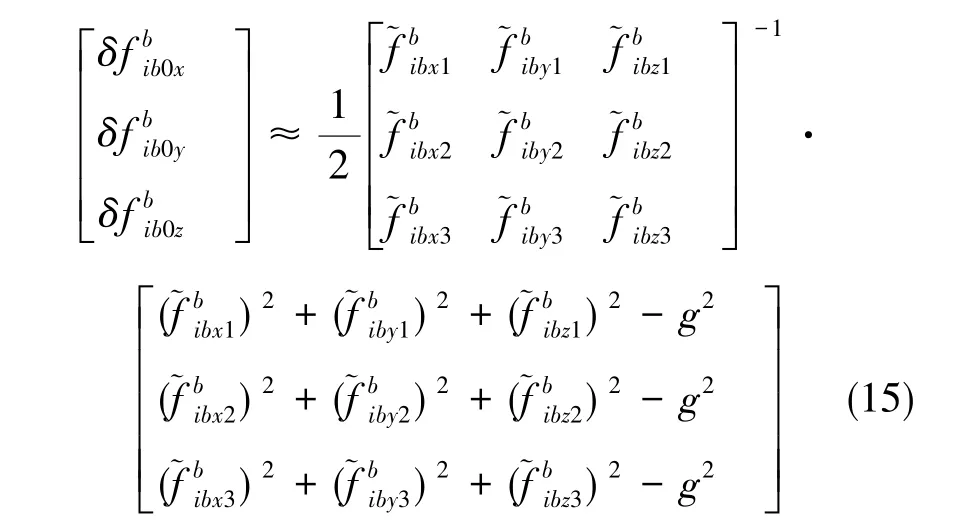
依次使x、y、z加速度敏感軸與重力矢量方向大致一致，可使加速度計(jì)零偏估計(jì)結(jié)果最優(yōu)。

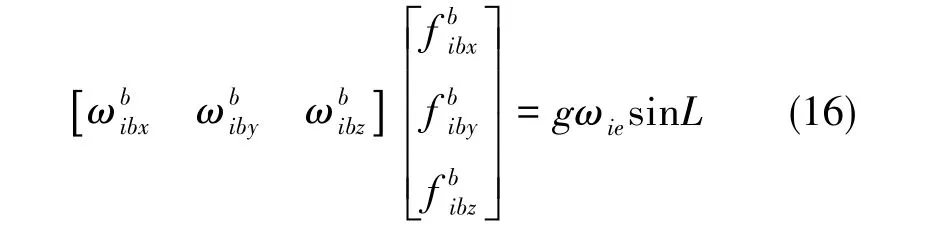
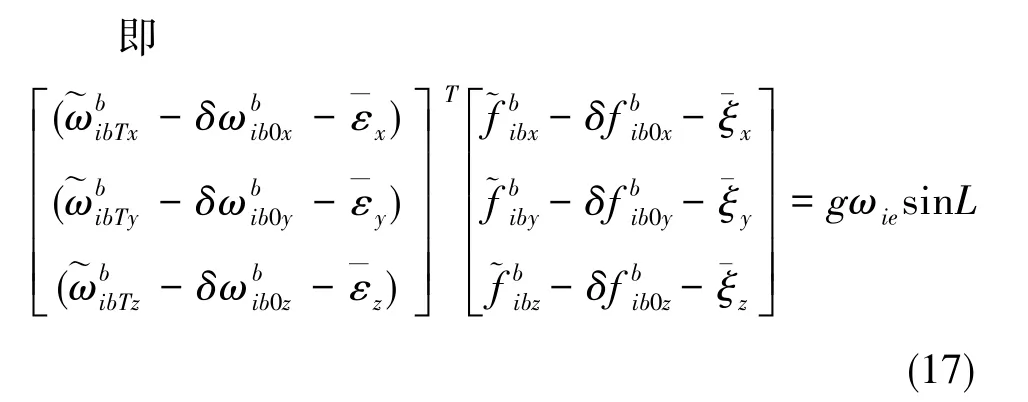
依次使x、y、z陀螺敏感軸與重力矢量方向大致一致，可使陀螺零偏估計(jì)結(jié)果最優(yōu)。

由于重力模值遠(yuǎn)大于地球自轉(zhuǎn)角速度模值，故式（18）的估計(jì)效果要優(yōu)于式（14）的估計(jì)效果。當(dāng)陀螺精度較低時(shí)，式（18）的優(yōu)越性更為顯著。上述方法同樣適合在極區(qū)的外場自標(biāo)定。

在中緯度地區(qū)外場標(biāo)定，當(dāng)慣導(dǎo)系統(tǒng)僅能繞z軸旋轉(zhuǎn)時(shí)，可分別將慣導(dǎo)系統(tǒng)的x軸、y軸分別大致朝向南北方向，四個(gè)位置的測量結(jié)果組成式（19）。

基于最小二乘即可求出陀螺常值漂移，優(yōu)點(diǎn)是不受加速度計(jì)誤差的影響。

3 實(shí)驗(yàn)驗(yàn)證及分析

3.1 實(shí)驗(yàn)準(zhǔn)備

為了驗(yàn)證所提出算法的有效性，本文進(jìn)行了溫控轉(zhuǎn)臺(tái)實(shí)驗(yàn)。溫控轉(zhuǎn)臺(tái)如圖2所示，將光纖陀螺慣導(dǎo)系統(tǒng)置于溫控轉(zhuǎn)臺(tái)中，實(shí)驗(yàn)具體設(shè)置為:在慣導(dǎo)系統(tǒng)斷電狀態(tài)下，－15℃保溫24h，確保系統(tǒng)內(nèi)部充分冷卻；系統(tǒng)開機(jī)，使環(huán)境溫度分別在1h和4h內(nèi)從－15℃上升到50℃，然后在50℃環(huán)境下進(jìn)行保溫，升溫過程中轉(zhuǎn)臺(tái)保持靜止。其中，1h的靜態(tài)溫控轉(zhuǎn)臺(tái)溫度變化和光纖環(huán)溫度變化如圖3所示。

圖2 光纖陀螺慣導(dǎo)系統(tǒng)實(shí)驗(yàn)溫控轉(zhuǎn)臺(tái)Fig.2 Diagram of FOG INS experiment temperature control turntable

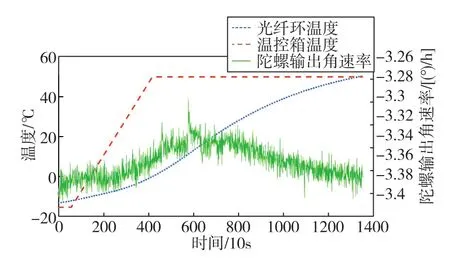
圖3 x軸光纖陀螺輸出與溫度的關(guān)系Fig.3 Relationship between the bias and the temperature for the FOG at x-axis

3.2 溫度漂移估計(jì)與補(bǔ)償

根據(jù)不同溫度段特征選取三個(gè)軸向光纖陀螺的溫度特征區(qū)間，如表1所示。相鄰溫度段的溫度漂移在端點(diǎn)處相同，溫度區(qū)間可以寫為兩側(cè)閉區(qū)間。由于慣導(dǎo)內(nèi)部溫度計(jì)示數(shù)（約－12℃）和溫箱溫度計(jì)示數(shù)（－15℃）不一致，故本文以慣導(dǎo)內(nèi)部溫度為準(zhǔn)，并選取－10℃作為溫度區(qū)間的起點(diǎn)。為了避免最小二乘法估計(jì)中的病態(tài)問題，本文利用了兩次不同升溫速率的實(shí)驗(yàn)數(shù)據(jù)（相同升溫差值，升溫時(shí)間分別為1h和4h）。使用本文提出的參數(shù)估計(jì)法對三軸光纖陀螺溫度漂移的不同溫度段溫漂參數(shù)進(jìn)行估計(jì)，角增量積分周期選為200s。將本文方法與傳統(tǒng)整體估計(jì)方法進(jìn)行比較，得到三個(gè)軸向的溫度漂移補(bǔ)償結(jié)果，如圖4所示。

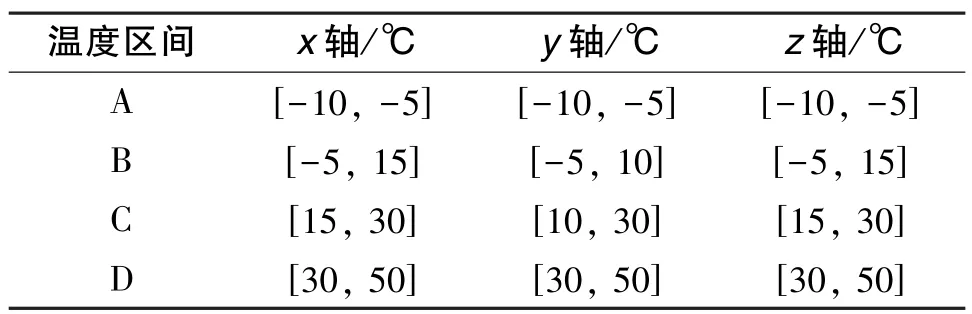
表1 三軸光纖陀螺溫度區(qū)間劃分Table 1 Temperature segments division of there-axis FOG

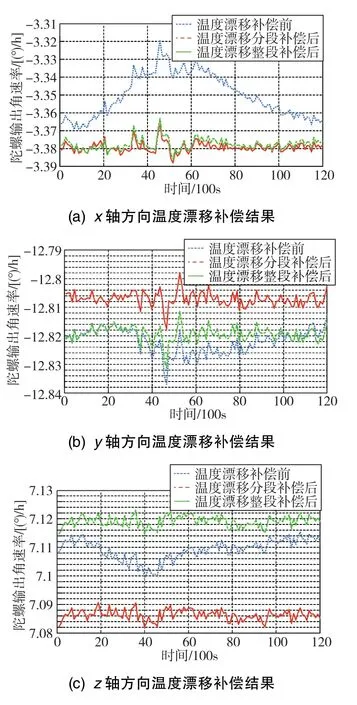
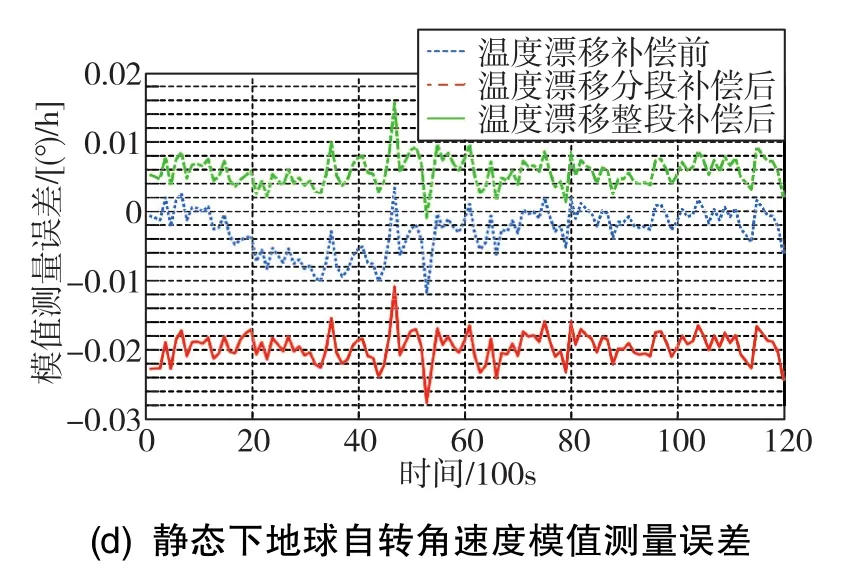
圖4 溫控轉(zhuǎn)臺(tái)1h升溫實(shí)驗(yàn)溫度漂移補(bǔ)償結(jié)果Fig.4 Compensation results of thermal drift in 1h heating test with temperature control turntable

由圖4可知，本文提出的方法將光纖陀螺由溫度導(dǎo)致的漂移誤差進(jìn)行了有效補(bǔ)償。通過上述基于角增量的最小二乘法參數(shù)估計(jì)方法得到的陀螺輸出補(bǔ)償結(jié)果如表2所示。由表2可知，x軸光纖陀螺相比y軸、z軸的溫度特性較差。本文提出的分段估計(jì)方法將慣導(dǎo)系統(tǒng)中三個(gè)軸向的溫度漂移分別補(bǔ)償了76.33%、41.98%、49.45%，而整體估計(jì)方法則分別補(bǔ)償了 73.70%、39.40%、48.47%，前者相比后者誤差均方差分別減小了2.63%、2.58%、0.98%。

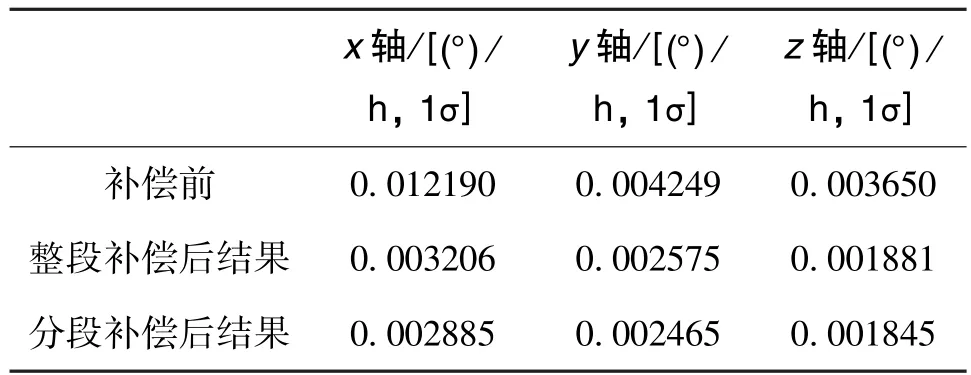
表2 分段估計(jì)與整體估計(jì)方法溫度漂移補(bǔ)償效果對比（波動(dòng)均方差）Table 2 Comparison of thermal drift compensation between piecewise and global estimation

應(yīng)注意到，在經(jīng)過溫度漂移補(bǔ)償后的三軸陀螺輸出中，零偏未被補(bǔ)償，接下來將利用基于地球自轉(zhuǎn)角速度的矢量模值觀測法對陀螺零偏進(jìn)行估計(jì)。

3.3 陀螺零偏估計(jì)與補(bǔ)償

為了補(bǔ)償上一節(jié)提到的溫度漂移補(bǔ)償后的陀螺輸出中含有的零偏，在－10℃環(huán)境下進(jìn)行保溫，分別將慣導(dǎo)系統(tǒng)x軸、y軸分別大致朝向南北方向靜置5min，將陀螺輸出進(jìn)行溫度漂移補(bǔ)償后使用式（19）進(jìn)行計(jì)算。根據(jù)當(dāng)?shù)氐乩砭暥群椭亓铀俣龋軌虻玫綔?zhǔn)確的三軸陀螺零偏分別為0.031（°）/h、－0.0035（°）/h、 －0.033（°）/h。 此處計(jì)算的為－10℃的陀螺零偏，其他溫度段的等效陀螺零偏可以通過式（5）得到。在升溫實(shí)驗(yàn)中，對陀螺輸出進(jìn)行溫度漂移和零偏補(bǔ)償后的結(jié)果如圖5所示。

圖5 1h升溫實(shí)驗(yàn)溫度漂移與零偏補(bǔ)償結(jié)果Fig.5 Compensation results of thermal drift and zero drift in 1h heating test

經(jīng)過地球角速度矢量模值觀測法零偏補(bǔ)償后的結(jié)果更加接近陀螺相對于慣性空間的真實(shí)角速率輸出，使用地球角速度矢量模值觀測法可以克服傳統(tǒng)多位置初始對準(zhǔn)陀螺零偏估計(jì)方法在極區(qū)（高緯度）不適用的缺點(diǎn)，因而提高了慣導(dǎo)系統(tǒng)的環(huán)境適應(yīng)性。

4 結(jié)論

本文針對角增量輸出式三軸光纖陀螺捷聯(lián)慣導(dǎo)系統(tǒng)的陀螺溫度漂移及常值零偏誤差參數(shù)估計(jì)問題，分別提出了一種基于角增量的分段最小二乘誤差估計(jì)方法和基于地球自轉(zhuǎn)角速度矢量模值觀測法的常值零偏估計(jì)方法。在建立光纖陀螺溫度漂移線性模型的基礎(chǔ)上，針對三軸光纖陀螺選擇不同的溫度段進(jìn)行劃分，繼而分別對三軸陀螺不同溫度段的溫度漂移參數(shù)進(jìn)行了參數(shù)估計(jì)，推導(dǎo)了不同溫度段間的邊界條件，并對各溫度段的零偏差異進(jìn)行了補(bǔ)償，解決了溫度漂移分段估計(jì)在不同溫變速率條件下不連續(xù)的問題。本文提出的方法相比傳統(tǒng)整體參數(shù)估計(jì)方法能夠更加細(xì)致地描述不同溫度區(qū)間的溫度特性。溫控轉(zhuǎn)臺(tái)升溫實(shí)驗(yàn)表明了本文提出的分段估計(jì)方法的有效性，本方法的補(bǔ)償效果優(yōu)于傳統(tǒng)整體參數(shù)估計(jì)方法。在三軸光纖陀螺溫度補(bǔ)償?shù)幕A(chǔ)上，使用地球自轉(zhuǎn)角速度模值觀測法對光纖陀螺的剩余零偏進(jìn)行了估計(jì)，得到了三個(gè)軸向的陀螺零偏。本文所提出的零偏估計(jì)方法不需要高精度轉(zhuǎn)臺(tái)，可適用于高緯度地區(qū)及極區(qū)環(huán)境下的外場標(biāo)定，提高了慣導(dǎo)系統(tǒng)的環(huán)境適應(yīng)性。