鐵道貨車車輪輪徑差與輪軌力關系的研究

向金蘭，曾 京，彭莘宇，李 浩

（西南交通大學1.力學與工程學院；2.牽引動力國家重點實驗室，四川 成都610031）

鐵路車輛在運行過程中由于輪軌磨耗不可避免會出現左右車輪輪徑產生差值的情況。 出于安全的考慮，一般會對車輪進行定期檢修，以保證差值在車輛安全許可范圍內，但鐵道車輛的輪徑差差值檢測，傳統上基本采用人工下車底測量，或將車輪拆卸后測量，耗費大量人力。 通過檢測車輛的輪軌力，找到輪軌力與車輪輪徑差的對應關系，由其對應關系，通過輪軌力便可以較好地反映出車輪運行狀態及輪徑差的差值大小。 基于此思路，首先制定了相應車輪輪徑差，再由動力學軟件模擬車輛運行狀態，輸出輪軌力及其他響應值，最后對其進行分析，得出車輪輪徑差差值與輪軌力的關系。

目前國內外對輪軌力與車輪輪徑差的關系研究尚未有準確的定義，但為大眾所知的是，輪徑差的存在一定會導致車輪的左右輪軌力出現差值，并且出現車輛橫移以及輪軸橫向力的變化，但對于它們間存在怎樣的對應關系，怎樣找出其對應的數值關系，國內外有關研究較少。 而對于輪軌力測試裝置[1-2]、輪徑差對于車輛動力學性能的影響相關研究則相對較多[3-6]，何彩穎、宋榮榮等[7]于2011 年對某C0-C0 機車的轉向架輪對橫向輪軌力進行了仿真分析，并模擬了輪對出現輪徑差，機車制動時輪軌力的變化，該研究驗證了實際運營機車出現輪徑差時的真實運營情況，但是對于輪徑差與輪軌力之間的對應關系尚未詳細探討。 南京浦鎮車輛廠的朱良政、肖天宇[8]于2017 年針對輪徑差對軌道車輛車輪產生的偏磨影響，分析了輪徑差對軌道車輛車輪磨耗影響受力情況，并且闡述了輪徑差對輪對蠕滑力與磨耗功率的影響。 大連交通大學的劉思瑩等[9]研究了輪徑差對機車動力學性能及輪軌接觸的影響，通過動力學仿真計算與有限元計算著重分析了輪徑差對機車動力學性能的影響及輪徑差對于輪軌接觸的影響。 但他們對于輪徑差與輪軌力之間關系的研究并未進行深入的探討。

1 動力學模型

目前國內鐵路貨車主要有C64K，C70，C80 等，轉向架主要為轉K2、轉K6 型轉向架，在本文中，建立C70 型貨車動力學模型，轉向架采用轉K6 型轉向架，各動力學參數如下。

車體質量14.2 t，載重70 t，車輛定距9.21 m，其他參數如表1 所示；由于研究內容僅關注同一輪對輪徑差與輪軌之間對應關系，根據中國關于貨車同一輪對的輪徑差限值≤1 mm，考慮實際運營中可能出現的情況，動力學模型中建立車輛-軸輪對輪徑差分別為0，0.5，1.0，1.5，2.0，2.5，3.0，3.5，4.0，4.5，5.0 mm，且以右輪輪徑小于左輪輪徑情況設定輪徑差；考慮到實際測量輪軌力裝置設置為運煤專線的空車線路，故而車輛設置為空載運行，車輛運行速度為80 km/h。

線路設置為1 000 m 直線軌道，分不施加激勵的簡單軌道及施加美國五級譜的有激勵一般軌道，動力學模型如圖1 所示。

表1 貨車車輛參數Tab.1 Vehicle parameters of goods vehicles

圖1 C70 貨車動力學模型Fig.1 C70 truck dynamics model

由于主要研究內容為探尋輪軌力與輪徑差的關系， 故而可以先由理想軌道模型整理得到大致關系，再添加軌道激勵，考慮實際情況因素來驗證該關系是否合理，最終得到結論。 輪徑差主要識別內容只是單一輪對，且只需獲得同一輪對左右兩輪的輪軌力值進行研究，車輛其他性能暫不進行考慮，故在此仿真中只設置單一輪對的輪徑差進行仿真求解，同時為了簡化計算，車輪設置為剛性體，暫不考慮車輪彈性對輪軌力的影響，輪徑差設置于車輛前進方向的一位輪對，步長0.5 mm，范圍為0～5 mm。

2 無激勵普通軌道輪軌力仿真結果

對上述工況進行仿真計算，并取同激勵情況下不同輪徑差的輪對響應值進行對比。為了方便分析，先取無激勵軌道的輪對左右側車輪輪軌垂向力、輪軌橫向力，有輪徑差輪對及正常輪對的橫向位移量，兩輪對輪軸橫向力進行對比分析。 選取同類型參數不同工況數據對比，由仿真分析得到的數據如圖2～圖6 所示。

圖2 輪徑差及左右車輪輪軌垂向力對應關系Fig.2 The relationship between wheel diameter difference and vertical force of left and right wheels

圖3 輪徑差及左右車輪輪軌橫向力對應關系Fig.3 The relationship between wheel diameter difference and lateral force of left and right wheel and rail

圖4 輪徑差及前后輪對橫向位移對應關系Fig.4 The relationship between wheel diameter difference and lateral displacement of front and rear wheel pairs

圖5 輪徑差及前后輪對輪軸橫向力對應關系Fig.5 The relationship between wheel diameter difference and lateral force of front and rear wheelsets

圖6 輪徑差及前后輪對輪軸橫向力對應關系（絕對值差值）Fig.6 Correlation between wheel diameter difference and lateral force of front and rear wheelset axle(absolute value difference)

分析數據不難得出一個規律：輪徑差差值與輪軌力存在對應關系， 并且由于輪徑差的影響，輪軌垂向力、橫向力、輪對橫移量、輪軸橫向力都會因輪徑差差值變化而變化。 輪軌垂向力的關系在圖2 中表現最為明顯，隨右輪滾動圓直徑的減少， 右側車輪的輪軌垂向力基本呈直線增長，而左側車輪輪軌垂向力基本呈直線減少，左右側輪軌力差值FZ 與輪徑差關系x 呈現為一次函數

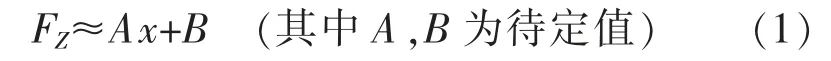
從其他響應特征來看， 基本也呈同樣的趨勢：右側車輪輪軌橫向力隨著輪徑差的增大而增大，左側車輪則隨輪徑差變大而減小，而隨著輪對左右輪徑差的增長，車輪輪軌橫向力的增長速度也隨著增長，左右側輪軌橫向力差值Fy與輪徑差差值x之間關系體現為二次曲線關系

此外，出現輪徑差的橫向位移要比正常輪對橫向位移要大，并且輪對的偏移方向為向輪徑值較小的車輪一側偏移，也呈一次函數關系。

在輪軸橫向力方面，由于輸出響應值為同一轉向架前后輪對輪軸橫向力，前后兩輪對的輪軸橫向力基本呈相反數狀態，不過隨著輪徑差的增大，輪對的輪軸橫向力也逐步增大，單個輪對輪軸橫向力Fsumy與輪徑差x 之間的關系同樣呈現為一次函數形式。

由輪徑差造成的輪對響應變化關系在輸出的輪軌垂向力、橫向力、輪軸橫向力及輪對橫向位移均有體現，并且分析能得到較為理想的對應關系。這里的仿真計算中，軌道是無激勵無缺陷的理想軌道，在實際中，是難以得到這樣的理想效果的，因而需要對軌道施加激勵后，再來驗證輪軌力與輪徑差之間是否依然遵守上述規律。

3 美國五級譜軌道激勵情況下的輪軌力輸出

由于上述分析建立在無激勵情況下，而實際應用中很難得到理想的軌道狀態，真實情況中需考慮軌道隨機不平順對車輛輪軌力的干擾。 因此以國際通用的美國五級譜（詳見參考文獻[9]）作為軌道不平順輸入，重新進行仿真。

3.1 美國五級譜激勵情況下左右輪軌垂向力對比

設置同樣輪徑差差值進行仿真并輸出同一輪對的左右輪軌力（此處選擇輪軌力的均值作為主要參數）進行分析，結果見圖7～圖8（方格點線圖為右側輪軌力，圓點線圖為左側，下同）。

由輪軌垂向力分析可以得到：在美國五級譜激勵情況下，同一輪對的左右輪軌垂向力也同樣出現了與無軌道激勵同樣的波動趨勢，左右輪輪軌垂向力差值與輪徑差差值還是基本呈正比例關系，這與無軌道激勵時的輪軌垂向力響應關系基本一致。

圖7 輪徑差及左右側輪軌垂向力對應關系圖（有激勵）Fig.7 Diagram of wheel diameter difference and vertical force on left and right side of wheel rail (with excitation)

圖8 輪徑差及左右側輪軌垂向力對應關系圖（有激勵）Fig.8 Diagram of wheel diameter difference and vertical force on left and right side of wheel rail (with excitation)

由數據整理可以大致得到車輛在空車情況下， 左右側輪軌垂向力差值FZ與輪徑差x 之間的一次函數關系式為

3.2 美國五級譜激勵情況下左右輪軌橫向力對比

與2.2 節中輸出輪軌力相似，仿真整理后得到以下結果：

在具有軌道激勵的情況下，橫向輪軌力出現較大振動，并不能直接得到一個確定的輪軌力值，如圖9，圖10 中的輪軌力值為車輛處于穩定運行狀態的輪軌力均值。

圖9 2.5 mm 輪徑差橫向輪軌力時域圖（有激勵）Fig.9 Lateral wheel/rail force time domain diagram of wheel 2.5 mm diameter difference (with excitation)

圖10 輪徑差及前后輪對橫向位移對應關系圖（有激勵）Fig.10 Diagram of corresponding relationspip between wheel diameter difference and lateral displacement of front and rear wheel pairs (with excitation)

從數據來看橫向力對于輪徑差響應更為敏感，沒有輪徑差時，輪對左右橫向輪軌力數值一致，但當輪徑差增大時，左右輪軌力差值有明顯差異變化，2.5 mm 輪徑差時，左右輪軌橫向力數值差為0.743 kN，并且隨著輪徑差的增大，差值也隨著增大，4 mm 時對應1.381 kN，5 mm 對應1.776 kN。 這里的輪軌力變化規律與無軌道激勵時的輪軌力變化規律基本一致。 從圖8 來看，左右側輪軌橫向力差值Fy與輪徑差關系x 更表現為一次函數關系，與無激勵情況下有所差別，但依然可以擬合為二次函數，其關系式表達為

3.3 前后輪對響應特征對比

同樣地，分析在美國五級譜激勵情況下的輪對橫向位移及輪軸橫向力響應規律，仿真結果整理得到圖11。

在軌道譜激勵情況下， 當輪對出現輪徑差時，輪對的前后橫移量及輪軸橫向力變化趨勢基本與無軌道激勵時保持一致。 數據整理，代入對應函數關系式中，得到輪對橫向位移Y 與輪徑差差值x 之間的關系式為

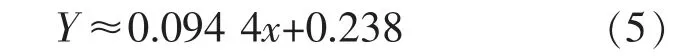
輪對輪軸橫向力Fsumy與輪徑差差值x 對應關系式

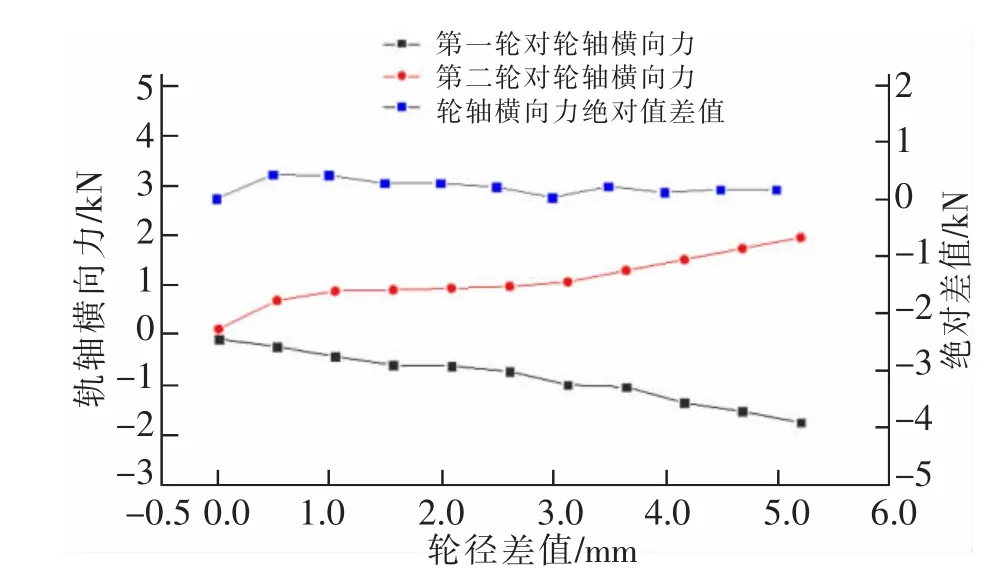
圖11 輪徑差及前后輪對輪軸橫向力對應關系圖（有激勵）Fig.11 Relational diagram of wheel diameter difference and lateral force of front and rear wheel pairs (with excitation)

4 結論

由上述分析可以得到：當輪對出現輪徑差時，車輪輪軌垂向力、輪軌橫向力、輪對的橫向位移以及輪對輪軸力都會出現較大變化，并且隨著輪徑差的增大，上述參量也隨著輪徑差的增大而增大，且在一定范圍內呈線性關系變化。 國內相關標準[11]規定同一輪對的左右輪徑差差值不得超過1 mm，由本文推導得到的關系式大致可以得到一個準許輪軌力評定值，可以為實際間接測量輪徑差差值提供一定參考。