基于強(qiáng)化學(xué)習(xí)的平行航班動(dòng)態(tài)定價(jià)

方 園，樂(lè)美龍

（南京航空航天大學(xué)民航學(xué)院，江蘇 南京 21100）

隨著航運(yùn)市場(chǎng)的不斷擴(kuò)大，各航空公司之間的競(jìng)爭(zhēng)越來(lái)越激烈。 大部分航線會(huì)有多家航空公司同時(shí)運(yùn)營(yíng)，這些具有相同起訖點(diǎn)的航班稱為平行航班。價(jià)格成為影響其收益的主要因素。航空公司之間的競(jìng)爭(zhēng)以及供求關(guān)系的變化導(dǎo)致航線產(chǎn)品的價(jià)值在不斷變化，不論是對(duì)航空公司還是旅客來(lái)說(shuō)，進(jìn)行動(dòng)態(tài)定價(jià)十分必要。 現(xiàn)有機(jī)器學(xué)習(xí)和大數(shù)據(jù)技術(shù)的發(fā)展以及航空市場(chǎng)的寬松環(huán)境也為動(dòng)態(tài)定價(jià)提供了有利的環(huán)境。

原有的較多收益管理都從艙位分配的角度進(jìn)行研究[1-2]，還有將艙位控制和定價(jià)同時(shí)進(jìn)行的[3]，現(xiàn)在逐漸轉(zhuǎn)向從價(jià)格的角度進(jìn)行收益管理。 Gallego G 等[4]最早研究多產(chǎn)品下的動(dòng)態(tài)定價(jià)問(wèn)題，他們將單產(chǎn)品的研究拓展到多產(chǎn)品的動(dòng)態(tài)定價(jià)中，采用強(qiáng)度控制的方法求解多產(chǎn)品的動(dòng)態(tài)規(guī)劃問(wèn)題，導(dǎo)出相應(yīng)的Hamilton-Jacobi-Bellman 方程得到漸進(jìn)最優(yōu)解。Zhang D 等[5]用馬爾可夫決策過(guò)程對(duì)多個(gè)相同目的地之間的可替代航班進(jìn)行動(dòng)態(tài)定價(jià)。 通過(guò)上下限和啟發(fā)式的方法進(jìn)行求解，并通過(guò)定期更新各時(shí)點(diǎn)的狀態(tài)來(lái)改變價(jià)格。 Akcay Y 等[6]建立了一種能捕捉縱向和橫向的產(chǎn)品異質(zhì)性的線性隨機(jī)效用框架， 并在此基礎(chǔ)上進(jìn)行多產(chǎn)品聯(lián)合動(dòng)態(tài)定價(jià)，采用微分方程進(jìn)行求解。 Gallego G 等[7]采用連續(xù)時(shí)間上的隨機(jī)博弈，他們利用仿射函數(shù)逼近的方法求解微分博弈，并獲得漸近均衡解。 曹海娜[8]和朱志愚等[9]采用MNL（multinomial logit model）選擇模型對(duì)平行航班進(jìn)行動(dòng)態(tài)定價(jià)。 以上這些研究大多采用近似的方法對(duì)NP 問(wèn)題進(jìn)行求解，使得求解結(jié)果不夠準(zhǔn)確。 目前有部分研究利用強(qiáng)化學(xué)習(xí)方法解決動(dòng)態(tài)定價(jià)問(wèn)題。 Han W 等[10]通過(guò)提前建立其他主體的決策模型并預(yù)測(cè)他們的價(jià)格來(lái)構(gòu)建自身的定價(jià)模型，使得問(wèn)題從多主體決策轉(zhuǎn)變成單主體決策，并采用改進(jìn)的Q 學(xué)習(xí)方法求解。王金田等［11］和陸慧[12]根據(jù)消費(fèi)者的選擇行為是否易受折扣的影響，將其分為兩大類，采用強(qiáng)化學(xué)習(xí)對(duì)雙賣家市場(chǎng)進(jìn)行動(dòng)態(tài)定價(jià)，但對(duì)消費(fèi)者選擇行為的考慮較為簡(jiǎn)單。 Rana R 等[13-14]利用帶資格跡的強(qiáng)化學(xué)習(xí)方法分析高峰時(shí)刻和非高峰時(shí)刻的定價(jià)區(qū)別，并考慮多個(gè)具有關(guān)聯(lián)性產(chǎn)品的定價(jià)問(wèn)題。 通過(guò)為其它關(guān)聯(lián)性產(chǎn)品對(duì)需求的影響設(shè)置參數(shù)，問(wèn)題仍轉(zhuǎn)變?yōu)閱沃黧w的強(qiáng)化學(xué)習(xí)問(wèn)題。文獻(xiàn)［15－17］研究智能電網(wǎng)的最優(yōu)動(dòng)態(tài)定價(jià)問(wèn)題。 通過(guò)顧客消費(fèi)模型構(gòu)建定價(jià)的環(huán)境， 同時(shí)將動(dòng)態(tài)零售定價(jià)問(wèn)題轉(zhuǎn)化為有限離散馬爾可夫決策過(guò)程（MDP），并采用Q 學(xué)習(xí)求解最優(yōu)定價(jià)策略。本文將在以往研究的基礎(chǔ)上增加對(duì)旅客類型，以及需求在各時(shí)間段內(nèi)的異質(zhì)性的考慮，并將智能電網(wǎng)相關(guān)研究中所采用的單主體動(dòng)態(tài)定價(jià)方法拓展至平行航班的多主體動(dòng)態(tài)定價(jià)問(wèn)題中。 相比于以往研究，得到的定價(jià)策略更加合理精確，且能有效地捕捉不同類型旅客的選擇行為，并有效提升航空公司收益。

1 系統(tǒng)模型

本系統(tǒng)中包含兩個(gè)重要的角色，分別是旅客和航空公司。 假設(shè)兩家航空公司各自運(yùn)營(yíng)的一個(gè)航班為平行航班，且出發(fā)時(shí)刻較為接近。兩個(gè)航班的旅客群體設(shè)為I。由于航線產(chǎn)品屬于易逝品，具有一定長(zhǎng)度的銷售區(qū)間。 在以往的大部分研究中，通過(guò)對(duì)銷售區(qū)間進(jìn)行細(xì)分，使得每個(gè)時(shí)間段至多只有一名旅客到達(dá)。 但這種細(xì)分方式導(dǎo)致?tīng)顟B(tài)非常多，使得實(shí)際問(wèn)題的求解時(shí)間大大增加。 另外，在航空公司的實(shí)際定價(jià)中，也不可能每銷售出去一個(gè)座位就重新定價(jià)，這會(huì)使得旅客產(chǎn)生負(fù)面情緒。 因此，本文考慮以天為單位，將銷售區(qū)間分為T 個(gè)時(shí)間段，每個(gè)時(shí)間段t 表示一天。通過(guò)機(jī)票可銷售價(jià)格的離散化，將其定義為價(jià)格集合A。集合的大小是確定且有限的。

在每個(gè)時(shí)間段t，兩家航空公司分別確定該航班的票價(jià)，旅客則根據(jù)剩余艙位數(shù)和當(dāng)前票價(jià)確定自身的購(gòu)票需求。航空公司的目標(biāo)是實(shí)現(xiàn)自身收益最大化。在銷售區(qū)間結(jié)束后，艙位沒(méi)有剩余價(jià)值。假設(shè)系統(tǒng)不考慮超售和團(tuán)隊(duì)旅客，且兩個(gè)平行航班的初始艙位數(shù)和各個(gè)時(shí)間段內(nèi)的可選擇價(jià)格都已知。

1.1 旅客行為建模

旅客行為具有兩個(gè)重要特征，分別是到達(dá)率和估值。 假設(shè)旅客的到達(dá)率λ 服從泊松分布。 此外，還需考慮旅客在兩個(gè)競(jìng)爭(zhēng)航班之間的選擇行為。 MNL 模型是一個(gè)隨機(jī)效用最大化模型，用來(lái)描述旅客在平行航班間的選擇。 假設(shè)每個(gè)旅客購(gòu)買機(jī)票i 后獲得的產(chǎn)品效用為：Ui=ui+εi，其中ui=υi+ηfi。 因此，Ui=υi+ηfi+εi，i=1，2。υi表示航班i 的平均價(jià)值，η 表示價(jià)格反應(yīng)系數(shù)，fi為機(jī)票的定價(jià)，εi為隨機(jī)變量， 用來(lái)描述不能觀測(cè)到的效用隨機(jī)項(xiàng)。 假設(shè)εi服從二重指數(shù)分布且各變量?jī)蓛上嗷オ?dú)立，將旅客放棄購(gòu)買航班機(jī)票的效用定義為0，則每個(gè)旅客的購(gòu)買概率為

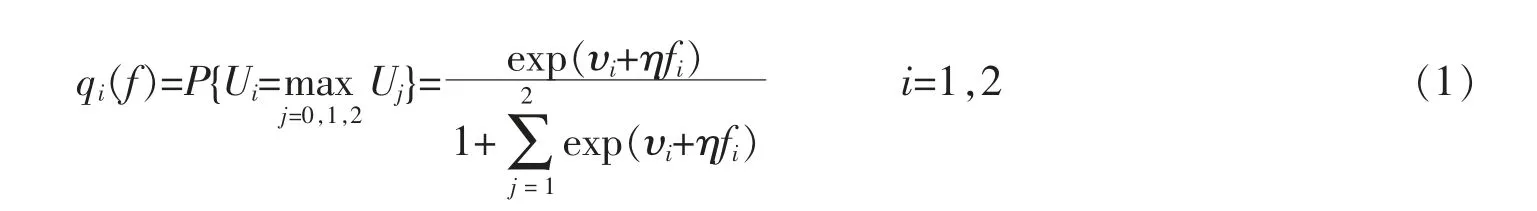
旅客放棄購(gòu)買任何一個(gè)航班機(jī)票的概率為

考慮到旅客的策略性行為，短視型旅客在到達(dá)的當(dāng)前時(shí)間段，會(huì)通過(guò)效用模型計(jì)算購(gòu)買概率，若效用值小于0，則會(huì)放棄購(gòu)買；若大于0，則選擇購(gòu)買效用高的航線。 而策略型旅客不止看到當(dāng)期的效用，還會(huì)和未來(lái)預(yù)期的效用進(jìn)行比較，這也就造成了計(jì)算的復(fù)雜性。 但旅客對(duì)于未來(lái)預(yù)期的收益并不能做到完全理性的判斷，只是一個(gè)自身的經(jīng)驗(yàn)估計(jì)值。 本文利用歷史該階段售價(jià)的均值計(jì)算未來(lái)預(yù)期的效用。

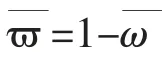
1.2 航線產(chǎn)品定價(jià)方建模

單航班的動(dòng)態(tài)定價(jià)問(wèn)題通常采用馬爾可夫決策過(guò)程（MDP）建模。 將單個(gè)航空公司的動(dòng)態(tài)定價(jià)問(wèn)題拓展至平行航班的定價(jià)問(wèn)題上，構(gòu)建多主體的隨機(jī)博弈Γ。 對(duì)一個(gè)具有兩個(gè)玩家和多個(gè)狀態(tài)的隨機(jī)博弈而言，可以看成是MDP 和矩陣博弈的組合，它是將MDP 拓展至兩個(gè)Agent 上，也是將矩陣博弈拓展多個(gè)狀態(tài)上。 隨機(jī)博弈同樣具有馬爾可夫性質(zhì)。

航線產(chǎn)品的定價(jià)方稱為Agent，分別用（i=1，2）表示。 兩個(gè)航班的座位總數(shù)分別用N1，N2表示。xit表示航班i 在時(shí)間段t 的剩余艙位數(shù)。隨機(jī)博弈可用元組表示為（S，A1，A2，r1，r2，p，γ）。S 表示狀態(tài)空間，用當(dāng)前時(shí)間段和兩個(gè)航班的剩余艙位數(shù)表示，st=（t，x1t，x2t）。 在每個(gè)時(shí)間段內(nèi)，有旅客到達(dá)并且購(gòu)票，狀態(tài)會(huì)發(fā)生變化，時(shí)間段t 會(huì)減1，兩個(gè)航班的庫(kù)存水平的狀態(tài)也會(huì)根據(jù)當(dāng)前時(shí)間段售出的艙位數(shù)而發(fā)生變化。

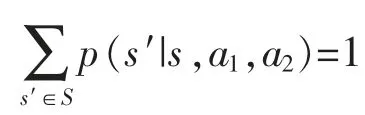
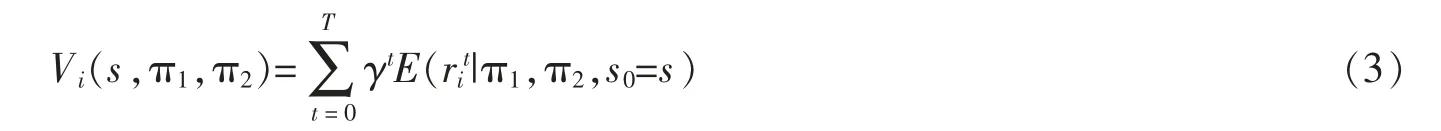
式中：E（rit|π1，π2，s0=s）表示在初始狀態(tài)s，策略為π1，π2時(shí)，在t 時(shí)間段的期望收益值。 則Vi（s，a1，a2）為從0開(kāi)始到結(jié)束的總收益。當(dāng)航班起飛后，不具有剩余價(jià)值。因此，最后的收斂條件為：Vi（（x，N，n），π1，π2）=0 或Vi（（x，n，N），π1，π2）=0；Vi（（0，x1，x2），π1，π2）=0。 銷售區(qū)間結(jié)束后，或者當(dāng)某個(gè)航班的艙位全部售出后的收益值為0。 當(dāng)滿足這兩個(gè)條件之一時(shí)，平行航班之間的競(jìng)爭(zhēng)結(jié)束。

每個(gè)特定狀態(tài)的矩陣博弈稱為階段博弈（stage game）。 由于兩個(gè)航班屬于不同航空公司，具有競(jìng)爭(zhēng)關(guān)系，在每個(gè)狀態(tài)下的階段博弈中尋找納什均衡策略以實(shí)現(xiàn)收益最大化。

定理1 在一個(gè)階段博弈中的納什均衡可以描述為n 個(gè)均衡策略的元組，使得Vi（（s，π1*，…，πi*，…，πN*）≥Vi（（s，π1*，…，πi，…，πN*）for all πi∈∏i。

用Vi*（s）表示納什均衡策略下的狀態(tài)值函數(shù)，Q*（s，a1，a2）表示在遵循納什均衡策略下的行動(dòng)值函數(shù)，則

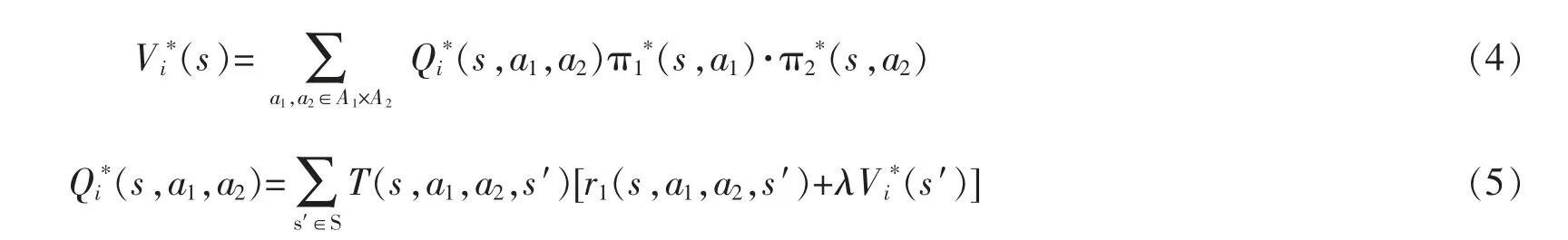
式中：πi*（s，a2）∈PD（Ai）是在玩家i 的納什均衡策略下在行動(dòng)ai上的概率分布。T（s，a1，a2，s′）=p（sk+1=s′|sk=s，a1，a2）是在給定狀態(tài)和聯(lián)合行動(dòng)后轉(zhuǎn)移至該狀態(tài)的概率。

由此，式（5）中的納什均衡可以重寫為

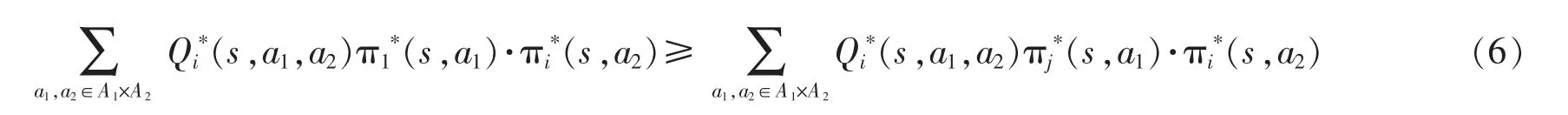
通過(guò)在每個(gè)階段博弈中求解納什均衡，以此作為在每個(gè)狀態(tài)下各Agent 能獲得的回報(bào)值，根據(jù)這個(gè)回報(bào)值進(jìn)而學(xué)習(xí)最優(yōu)定價(jià)策略。

2 算法設(shè)計(jì)

通過(guò)對(duì)旅客和航空公司定價(jià)方分別建模，利用強(qiáng)化學(xué)習(xí)算法求解馬爾可夫博弈。 強(qiáng)化學(xué)習(xí)不需要知道環(huán)境的具體模型，只依賴獲得的獎(jiǎng)勵(lì)學(xué)習(xí)最優(yōu)行動(dòng)，它是多Agent 系統(tǒng)的自然選擇。 將旅客的選擇行為作為強(qiáng)化學(xué)習(xí)的環(huán)境，每個(gè)Agent 通過(guò)與環(huán)境交互學(xué)習(xí)最優(yōu)策略。 在單Agent 的強(qiáng)化學(xué)習(xí)環(huán)境中，環(huán)境是相對(duì)穩(wěn)定的。 而多Agent 系統(tǒng)中，環(huán)境中還包括其他Agent 的行動(dòng)和狀態(tài)，即其他Agent 策略的改變也會(huì)影響自身最優(yōu)策略，因此環(huán)境是動(dòng)態(tài)多變的，這對(duì)算法的收斂性會(huì)帶來(lái)影響。此外，在單主體的強(qiáng)化學(xué)習(xí)中，需要存儲(chǔ)動(dòng)作狀態(tài)Q 值。 而多主體環(huán)境中，隨著主體的增加，狀態(tài)空間也增大，聯(lián)合動(dòng)作空間呈指數(shù)型增長(zhǎng)。 因此，多智能體系統(tǒng)的維度非常大，計(jì)算也變得更加復(fù)雜。 本文通過(guò)對(duì)時(shí)間段和剩余座位數(shù)都做了相應(yīng)的處理以減少狀態(tài)數(shù)。

2.1 環(huán)境設(shè)置

環(huán)境設(shè)置的目標(biāo)是創(chuàng)建一個(gè)虛擬的旅客人群，用來(lái)模擬在競(jìng)爭(zhēng)市場(chǎng)中對(duì)市場(chǎng)策略的反應(yīng)，作為強(qiáng)化學(xué)習(xí)的學(xué)習(xí)環(huán)境。 由于旅客自身的異質(zhì)性及其購(gòu)票時(shí)的策略行為，將旅客分為4 種類型。 對(duì)每種類型的旅客，對(duì)其設(shè)置到達(dá)概率、策略程度和離散選擇模型的參數(shù)。 具體步驟如下：

1） 根據(jù)該時(shí)段內(nèi)各類型旅客的到達(dá)率模擬旅客的到達(dá)數(shù)；

2） 根據(jù)旅客的離散選擇模型和策略程度確定各類型旅客在該價(jià)格下的選擇概率，若概率大于0，則選擇購(gòu)買概率高的航班；若概率小于0，則放棄購(gòu)買。

2.2 Nash-Q 算法

在多主體環(huán)境中， 對(duì)Q 學(xué)習(xí)算法進(jìn)行拓展， 將最優(yōu)Q 值定義為在Nash 均衡中收到的Q 值， 表示為Nash-Q 值。 計(jì)算納什均衡需要已知自身和對(duì)方的收益值和狀態(tài)值，因此需要維護(hù)多個(gè)Q 值表。 在每一次階段博弈中利用Lemke-Howson 算法計(jì)算納什均衡解：（Q1t（st+1，·），…，QMt（st+1，·）），從而計(jì)算出在各狀態(tài)下的各Agent 均衡收益值NashQti（s）。 用這個(gè)值對(duì)每個(gè)Agent 的Q 值進(jìn)行更新。 Q 值的更新規(guī)則為

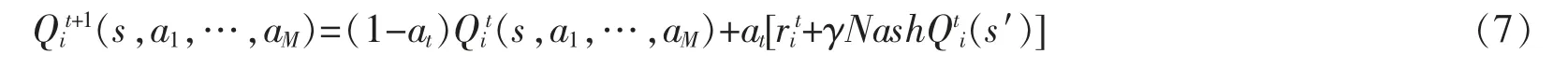
其中at是學(xué)習(xí)率，M 為Agent 的個(gè)數(shù)。 通過(guò)這些Q 值的迭代計(jì)算，最后收斂至一個(gè)穩(wěn)定值，從而獲得最優(yōu)定價(jià)策略。 據(jù)此，Nash-Q 算法的流程如下所示：

步驟一：初始化時(shí)間段t，初始狀態(tài)s0，對(duì)每個(gè)Agent 設(shè)置索引i；

步驟二：對(duì)所有的s∈S，以及ai∈Ai，初始化Qit（st，a1，…，aM）=0；

步驟三：與旅客環(huán)境進(jìn)行交互，通過(guò)Lemke-Howson 算法獲得納什均衡解，確定所有玩家的行動(dòng)ait后，從而計(jì)算收益值rt1，…，rtM并確定下一個(gè)狀態(tài)st+1=s′，對(duì)每個(gè)i，利用公式（7）更新Q 值；

步驟四：讓t=t+1，若t 為最終狀態(tài)對(duì)應(yīng)的時(shí)間段，則結(jié)束該循環(huán)；否則，返回至步驟三。

其中各個(gè)階段的狀態(tài)S，做出了相應(yīng)的簡(jiǎn)化。狀態(tài)中xit，不用真實(shí)的剩余座位數(shù)來(lái)表示，而是將一個(gè)區(qū)間范圍內(nèi)的剩余座位數(shù)投射到一個(gè)值上以表示當(dāng)前剩余座位數(shù)的狀態(tài)。 這大大減少計(jì)算過(guò)程所需的存儲(chǔ)空間，也加快了求解速度。

2.3 WoLF-PHC 算法

策略梯度爬升（PHC，policy hill climbing）算法的本質(zhì)是在混合策略空間中表現(xiàn)出梯度爬升。 PHC 方法不需要知道玩家最近執(zhí)行行動(dòng)的信息，以及對(duì)手當(dāng)前策略的信息，這可以減少算法所需的存儲(chǔ)空間并且符合實(shí)際的競(jìng)爭(zhēng)環(huán)境。 非Agent 選擇最高值行動(dòng)的概率會(huì)以學(xué)習(xí)率δ∈（0，1]增加，因此策略在不斷提升。PHC算法能保證在算法中學(xué)習(xí)的Agent 是理性的，即如果其他玩家的策略收斂至穩(wěn)定的策略時(shí)，那么自身的學(xué)習(xí)策略也會(huì)收斂至對(duì)其他玩家策略的最佳反應(yīng)策略。

WoLF-PHC 算法是PHC 算法的拓展[18]。 它的關(guān)鍵點(diǎn)為：①兩個(gè)學(xué)習(xí)率；②采用平均策略來(lái)近似均衡策略以確定輸贏。WoLF 準(zhǔn)則用來(lái)修正學(xué)習(xí)率。算法有兩個(gè)不同的學(xué)習(xí)率：δw表示贏時(shí)的學(xué)習(xí)率，δl表示輸時(shí)的學(xué)習(xí)率，δl大于δw。 當(dāng)Agent 輸時(shí)，學(xué)習(xí)的要比贏的時(shí)候快，這使得當(dāng)Agent 學(xué)習(xí)得比期望糟糕時(shí)，能對(duì)其他Agent 策略的變化適應(yīng)得更快；當(dāng)學(xué)習(xí)得比期望好時(shí)，要學(xué)得更謹(jǐn)慎。 這也給其他Agent 足夠的時(shí)間來(lái)適應(yīng)策略的變化。 平均策略旨在取代未知的其他Agent 均衡策略，它和當(dāng)前策略的不同被用作確定算法贏輸?shù)臉?biāo)準(zhǔn)。在很多博弈中，平均貪婪策略在實(shí)際上是近似均衡策略的，這是均衡發(fā)揮作用的驅(qū)動(dòng)機(jī)制。WoLF 準(zhǔn)則使得PHC 算法在自身博弈中可以收斂至納什均衡解。 由此， 該算法在保留理性的基礎(chǔ)上增加了收斂的性質(zhì)，使其能收斂至其中的一個(gè)納什均衡解。 收斂性質(zhì)將從下文的幾個(gè)典型案例計(jì)算來(lái)開(kāi)展。 Agent i 的Q 學(xué)習(xí)更新規(guī)則如下：

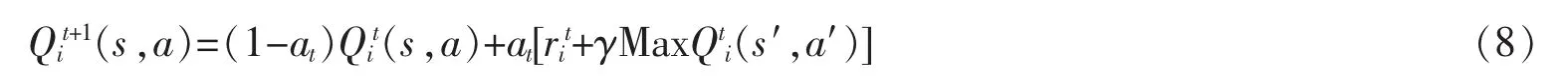
據(jù)此，設(shè)計(jì)WoLF-PHC 算法如下所示：

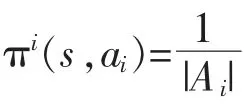
步驟二：對(duì)每一次迭代，

1） 在當(dāng)前狀態(tài)下基于一個(gè)混合探索-利用策略選擇行動(dòng)ac，執(zhí)行行動(dòng)后觀察收益ri以及下一個(gè)狀態(tài)s′；

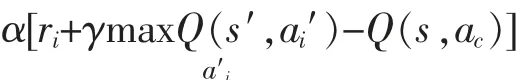
C（s）=C（s）+1，

4） 更新πi（s，ai），πi（s，ai）＝πi（s，ai）+Δsai，?ai∈Ai，其中

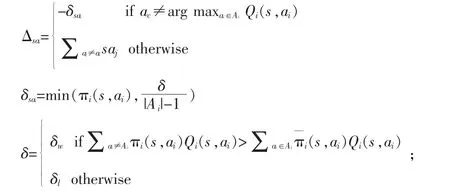
步驟三：更新S＝S′，若S 為最終狀態(tài)，結(jié)束該循環(huán)；否則，返回至步驟二。

此算法的狀態(tài)S 所包含的剩余座位數(shù)變量的設(shè)置同Nash-Q 算法一致。

3 仿真分析

假設(shè)兩個(gè)航班的參數(shù)一致。可銷售的票價(jià)集為{10，15，20，25，30}，總座位數(shù)均為50。假設(shè)剩余銷售期為10 天，對(duì)其進(jìn)行離散化處理，使得每天為一個(gè)時(shí)間段。 狀態(tài)包括兩個(gè)航班的剩余座位數(shù)以及當(dāng)前的時(shí)間段。其中，變量xit，將每5 個(gè)座位數(shù)為一個(gè)狀態(tài)，即將剩余艙位數(shù)除以5 取整作為當(dāng)前的剩余艙位數(shù)狀態(tài)。 對(duì)旅客仿真環(huán)境中的參數(shù)進(jìn)行設(shè)置，建立仿真環(huán)境。 參數(shù)設(shè)置為：?=0.4，φs=0.6，φm=0.6，βLS=0.2，βHS=0.1，不同類型旅客設(shè)定不同的λ，υi，η。 Nash-Q 算法中的參數(shù)設(shè)置為：αi=0.1，γ=0.9。 WoLF-PHC 算法中的參數(shù)設(shè)置為：αi=0.1，γ=0.9，δ＝0.000 1。

通過(guò)案例計(jì)算，Nash-Q 算法在5 000 次左右收斂，WoLF-PHC 算法在100 000 次左右收斂，表明兩種算法在實(shí)際問(wèn)題中都具有較好的收斂性。 Nash-Q 算法收斂所需的迭代次數(shù)要少于WoLF-PHC 算法，但WoLF-PHC 算法的收斂速度明顯優(yōu)于Nash-Q 算法。 這是符合實(shí)際情況的，因?yàn)镹ash-Q 算法在每個(gè)階段中都會(huì)計(jì)算納什均衡解，而WoLF-PHC 算法只能利用平均策略來(lái)近似策略，這使得其需要更多的迭代后才能收斂。 而也正因?yàn)镹ash-Q 算法需要在每一次階段博弈時(shí)計(jì)算納什均衡解，這會(huì)大大增加求解時(shí)間，且該算法需要已知自身和競(jìng)爭(zhēng)對(duì)手雙方的Q 值，這對(duì)于存儲(chǔ)空間的要求也有所增加。因此，WoLF-PHC 算法不論是在求解時(shí)間還是耗費(fèi)的存儲(chǔ)空間上都要優(yōu)于Nash-Q 算法。

表1 是航班在各個(gè)時(shí)間段的定價(jià)。 索引行為距離離港日期的時(shí)間，0 為停止售票的時(shí)間點(diǎn)。 Strategy 1為旅客的保留價(jià)格穩(wěn)定不變時(shí)的定價(jià)策略，Strategy 2 為航班在旅客保留價(jià)格隨時(shí)間而變時(shí)的定價(jià)策略，Strategy 3 和Strategy 4 考慮策略型旅客及保留價(jià)格變化的定價(jià)策略，且Strategy 4 的旅客策略程度的參數(shù)設(shè)置的要高于Strategy 3，由此可以看出策略程度對(duì)價(jià)格制定也會(huì)產(chǎn)生一定的影響，使得整體制定的價(jià)格都稍低一些。 從整體上看，由于航空旅客到達(dá)的特點(diǎn)，機(jī)票的價(jià)格曲線處于一個(gè)增長(zhǎng)的趨勢(shì)。 但由于旅客保留價(jià)格的變化及其策略行為使得航空公司需要不斷的調(diào)整價(jià)格，這也就導(dǎo)致價(jià)格在增長(zhǎng)的過(guò)程中會(huì)出現(xiàn)一些波動(dòng)，這些波動(dòng)能更好地適應(yīng)旅客行為的變化。將定價(jià)策略放到仿真環(huán)境中模擬，得到的收益相比于傳統(tǒng)方法提升約1.34%。

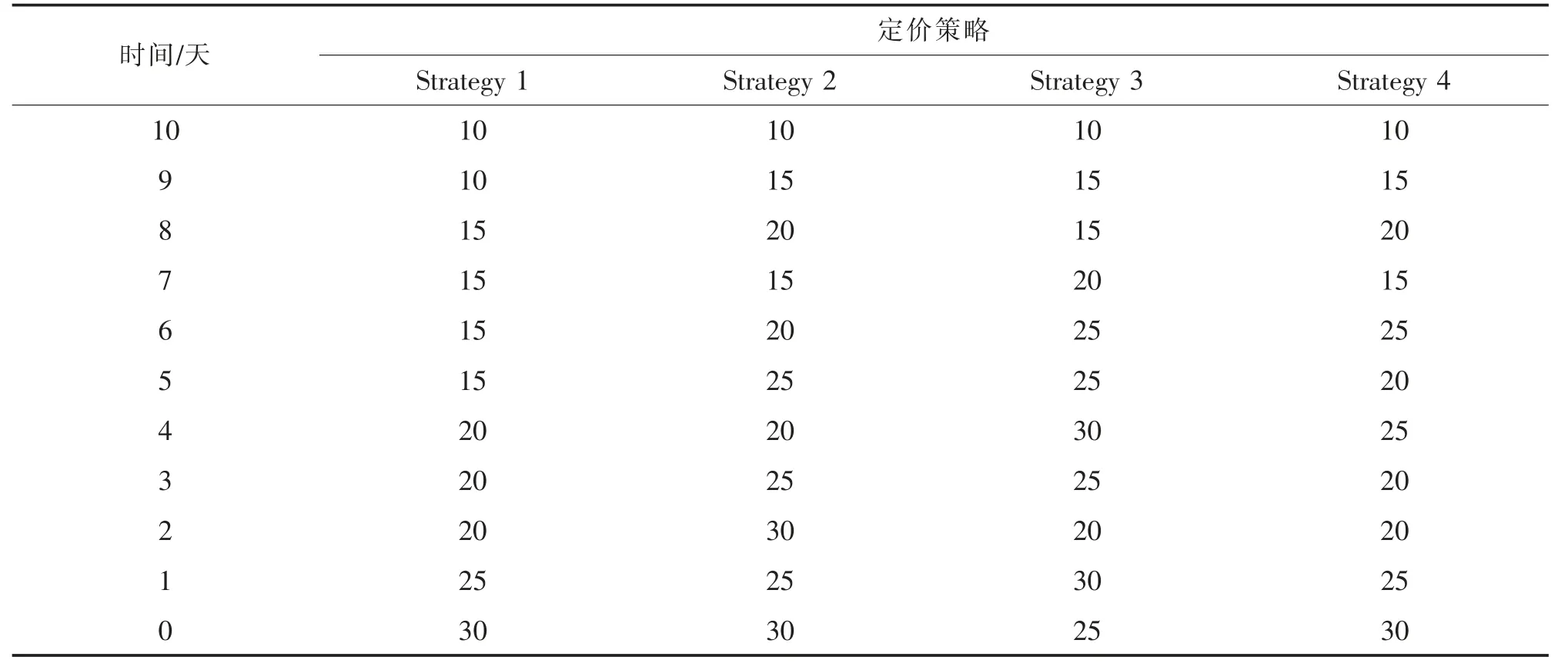
表1 航班定價(jià)策略Tab.1 The pricing strategy of flight tickets 元

4 結(jié)論

利用強(qiáng)化學(xué)習(xí)算法求解平行航班的動(dòng)態(tài)定價(jià)問(wèn)題，發(fā)現(xiàn)該算法對(duì)多主體的動(dòng)態(tài)定價(jià)問(wèn)題具有較好的適應(yīng)性，且能在有限步驟內(nèi)得到收斂，計(jì)算時(shí)間相比于傳統(tǒng)的近似計(jì)算方法較短且更加精確。 通過(guò)Nash-Q 算法和WoLF-PHC 算法的求解結(jié)果比較，發(fā)現(xiàn)WoLF-PHC 算法在求解時(shí)間上都優(yōu)于Nash-Q 算法，且Nash-Q 算法在維護(hù)Q 值表上耗費(fèi)的空間較大。此外，WoLF-PHC 算法在不同的旅客環(huán)境中，定價(jià)策略也會(huì)發(fā)生相應(yīng)的變化，能較好地適應(yīng)旅客環(huán)境的變化。由于航空旅客到達(dá)策略與其他行業(yè)有所不同，高消費(fèi)的旅客往往到出發(fā)前期才會(huì)購(gòu)買機(jī)票，而低消費(fèi)的旅客會(huì)早早的選擇進(jìn)行購(gòu)票，使得航空機(jī)票在整體上呈現(xiàn)出增長(zhǎng)趨勢(shì)。 另外，由于旅客的策略性行為，以及保留價(jià)格分布的變化，這也使得航空機(jī)票在定價(jià)過(guò)程中會(huì)出現(xiàn)一些波動(dòng)以適應(yīng)旅客的隨機(jī)行為。 WoLF-PHC 算法在平行航班的動(dòng)態(tài)定價(jià)問(wèn)題中的表現(xiàn)優(yōu)于Nash-Q 算法，且得到的定價(jià)策略能有效地增加航空公司收益，對(duì)航空公司在越來(lái)越劇烈的競(jìng)爭(zhēng)市場(chǎng)中立于不敗之地具有重要作用。