基于多目標優化技術的發動機罩加強筋布局設計研究

黃 鋒 汪興興 何彥虎 葛禹錫

1(湖州職業技術學院機電與汽車工程學院 浙江 湖州 313000)2(南通大學機械工程學院 江蘇 南通 226019)3(奧托立夫(上海)汽車安全系統研發有限公司 上海 201800)

0 引 言

發動機罩殼是車輛系統中的重要零部件，作為車身的重要覆蓋件之一，對車輛發動機等起到保護作用[1-2]，其性能好壞直接影響整車性能。它能有效地將汽車發動機與復雜外界環境隔開，確保車輛發動機的正常工作，且不受外界因素干擾。車輛結構中，發動機罩殼主要由內外板及中間的加強筋等結構件焊接而成，內板起到對發動機等隔離保護，外板和加強筋則是為了加強罩殼的剛度，預防車頭受撞或外力沖擊時，出現罩殼乃至車頭結構過大的損壞性變形。因此，對于車輛結構設計中，發動機罩殼的設計和結構力學性能優化等具有重要的作用和研究意義。由于汽車行駛的路面狀況復雜多變，車輛行駛過程中時刻處于微觀和宏觀上的顛簸與抖動，使得發動機罩殼在結構性能改進設計中，不僅需考慮其靜剛度特性，還需提高自身的低階固有頻率，使其具備抑制外界振動的能力[3]。

為了改善發動機罩殼的結構力學性能，國內已有相關學者進行了研究，并取得了一些成果。李立君等[4]采用了CAE技術并對罩殼沖壓工藝的改進，進而提高發動機罩殼的結構力學性能。陳越等[5]采用復合材料替換鋁合金作為發動機罩殼的材料，并采用復合材料優化設計改善了罩殼的結構力學特性。然而，這些方法所設計和改進設計的罩殼均基于工程師設計經驗的傳統設計方法，對于設計結果的客觀性依據不足，雖一定程度上改善了結構的力學性能，但常導致所設計的結構重量過大等缺點。隨著計算機技術和優化技術的不斷推廣，基于傳統設計方法的罩殼結構設計已逐漸不被認可，因此，基于現代設計方法[6]設計一款結構性能較優的發動機罩殼已是亟待解決的問題。將現代設計方法應用于高精尖端領域具有重要的意義[7]。

本文以校企合作單位的某款車型的發動機罩殼作為研究對象，采用多目標拓撲優化技術，使罩殼不僅實現了多目標優化，即結構靜態剛度和一階固有頻率均有所提高，還實現了結構輕量化設計。優化問題中采用水平集方法，目的在于獲取優化結果中較為清晰的模型邊界。該現代設計方法和多目標優化理論等為實際工程結構領域中的結構優化與設計等提供了重要的理論借鑒和可行性設計方案。

1 罩殼的有限元前處理模型

1.1 發動機罩殼的有限元模型

本文為校企合作單位某款車型的發動機罩殼，罩殼尺寸長約1 160 mm、前后寬度約1 450 mm，如圖1所示，采用Catia對罩殼進行CAD幾何建模。

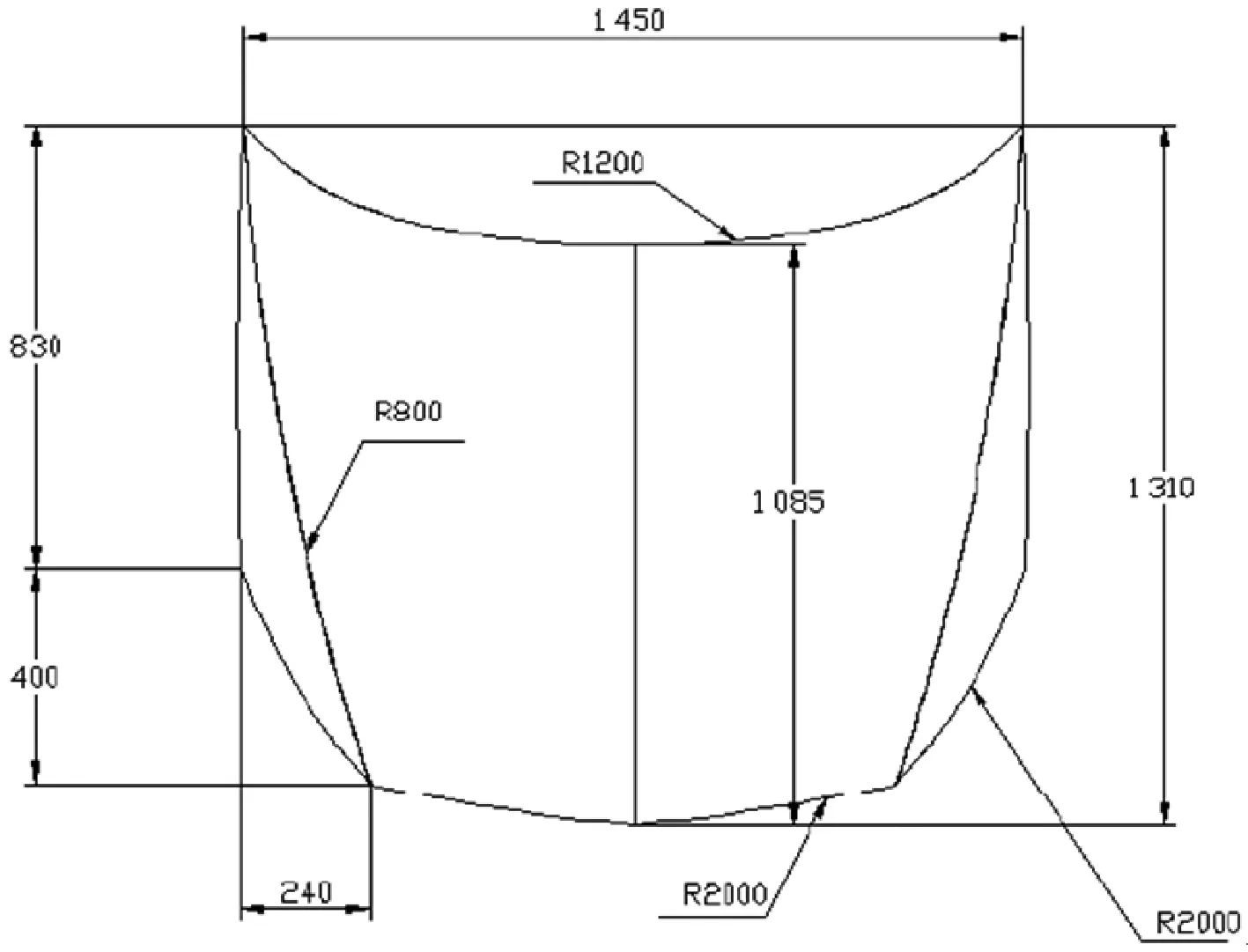
(a) 模型尺寸

(b) CAD模型圖1 罩殼幾何模型

罩殼材料主要為冷軋鋼板ST14材料，厚度一般為0.7～1.5 mm，基于《機械設計》手冊可查詢得到罩殼的材料屬性和力學性能參數，如表1所示。

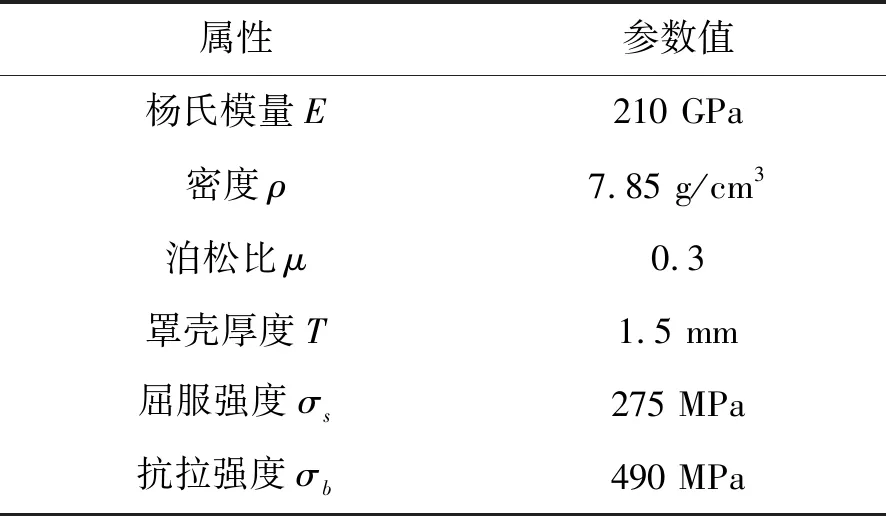
表1 發動機罩殼的結構參數

1.2 發動機罩的工況條件

車輛駕駛過程中，因復雜的外部環境如凹凸不平的地面、多變的天氣和來自外部環境的干擾因素等，使發動機罩不僅需具備一定的剛度特性用以抵抗外界沖擊，還需具備較高的振動抑制能力。對于通用型車輛發動機罩殼的工況條件，已有相關學者做了實驗檢測和分析，并取得了一定的成就[5]。與此同時，結合合作單位對發動機罩殼的工況測試和總結，可得發動機罩殼主要受到多個工況條件，如表2所示。

表2 發動機罩殼的多個工況條件

采用HyperMesh對發動機罩殼進行有限單元網格離散，賦予其冷軋鋼板ST14材料屬性并進行工況條件設置后的有限元前處理模型，如圖2所示。

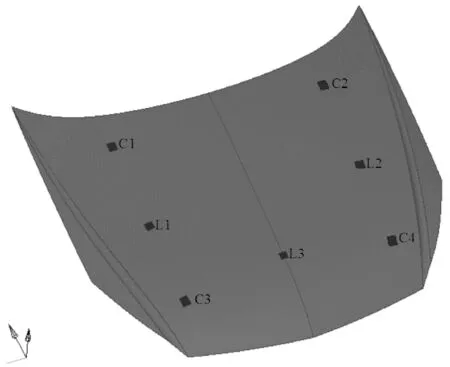
圖2 罩殼的工況條件

2 多目標優化理論

2.1 水平集法

水平集法是封閉曲線族p(x(t),t)關于時間t的變化情況，又稱為最佳解搜索方法[8]。p(x(t),0)為t=0時封閉曲線位置，p(x(t),t)為隨時間t變化的封閉曲線，如圖3所示。

圖3 關于時間t的封閉曲線變化

依據時間t的封閉曲線任意點速度v，該封閉曲線應滿足的微分方程為：

(1)

通常，對于封閉曲線的微分方程作為符號距離函數，其表示與封閉曲線的為最近任意點p(t)。此外，函數為正，表示該點位于封閉曲線內側，反之亦然。

依據微分方程原理，式(1)等式左側的首項為封閉曲線的負法線向量：

(2)

從而，式(1)可變為水平集公式；

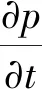
(3)

從式(3)中可得，該方法對于結構幾何形狀的搜索只與其速度相關，即面對不同拓撲變化的幾何邊界，封閉曲線始終呈現連續性，故應用領域和層次較廣。

為了對結構幾何邊界有精準的追蹤，確定水平集函數p(x(t),t)所處的位置，最終獲得最佳的水平集優化解，本文引入了修正后的符號距離函數：

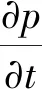
(4)

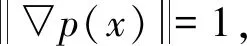
2.2 靜剛度—單目標優化模型

對于設計域內的水平集法，其動態表現形式如圖4所示。

圖4 水平集法結構演化

依據圖3和圖4，基于水平集函數p(x(t),t)的結構設計域的隱式關系為：

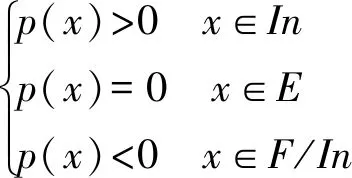
(5)

綜上所述，基于水平集優化模型推理[9-10]，對于發動機罩構建以靜態柔度最小化為目標，以優化前后的體積比和結構應力為約束條件的優化數值模型為：

(6)

u|?In=u0?ν∈U

式中:C(x)為結構靜態柔度；Eijkl為結構的彈性模量；εij、εkl為結構的應變張量。

2.3 動態固有頻率—單目標優化模型

眾所周知，當外界對物體產生的激勵接近物體的固有頻率時，物體常會出現共振破壞現象，為了防止“共振現象”，需對發動機罩殼的低階固有頻率進行改進設計，使其避開外界激勵頻率[11]。發動機罩殼的一階固有頻率高低能真實地反映發動機罩殼乃至整車的動剛度特性，因此，模態分析對于結構動態特性研究乃至深層次動力學分析等具有重要的研究意義和借鑒作用。

本文以發動機罩殼作為研究對象，基于水平集法，以單元密度為設計變量，以一階固有頻率為優化目標，以優化前后的體積比和許用應力值為約束條件構建其動態拓撲優化模型。然而，對于模態拓撲優化過程中，因結構單元材料的刪除，常會導致空洞區域的集中應力變大，固有頻率失真現象明顯。為了避免這類病態現象和目標函數的震蕩問題。本文采用由文獻[12]提出的平均頻率法，對優化模型中的目標函數進行了修正，基于平均頻率法對目標函數，即一階固有頻率的修正公式為：

(7)

式中:Λi為修正的第i階固有頻率值，本文中取i=1；Λi0為第i階的初始固有頻率值；λi0為第i階的特征值，為常數；s為給定常量；ωi為第i階加權因子；λi為第i階的特征值；m為需考慮固有頻率的階次數目；n為修正決定因子。

本文研究中為了簡化優化步驟，基于文獻[12]，取n=-1，則優化目標為式(7)中的首項，即Λ1,1。優化模型為：

(8)

s.t.u|?In=u0?ν∈U

S(x)≤[S]

?x∈In

式中:H(x)為Heaviside函數；S(x)為優化后結構的應力值；[S]為結構的許用應力值；ve為第e個單元體積；ρe為第e個單元的密度；f為優化前后的體積分數；V0為結構初始體積值。

3 靜動態多目標優化模型

3.1 基于層次分析法的單目標權重因子

層次分析法是基于數理統計的決策方案，通過定性定量的方法對方案進行準則層次化，客觀地求出各方案的權重因子[13]。該方法屬數理統計學范疇，由Saaty于1970年代初提出。該方法簡單、有效且避免了傳統上依據工程師設計經驗判定方案的重要性，避免了各目標的權重因子設定的主觀干擾性和不嚴謹性。

決策的層次分析法采用了數理統計中的特征矢量法[14]，該方法是給定加權特征向量E與決策矩陣J的右乘：

(9)

本文對發動機罩殼的多目標優化問題[15-16]研究中，主要考慮了靜態剛度和動態一階固有頻率，依據文獻[14]中采用層次分析法的決策矩陣原理，可得本文中的決策矩陣構型為：

(10)

式中：Jij為第i、j個目標函數在決策中的重要性參數。基于發動機罩的產品結構設計要求和相關研究基礎，本文對發動機罩殼的研發中，抑制外界激勵能力特性較重要于罩殼的剛度特性。依據各子目標函數的重要性參數[14]，可得本文的決策矩陣為：

(11)

從而，可求得式(11)中的特征值數組及其對應的特征向量為：

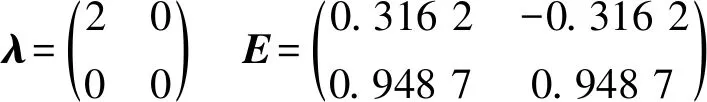
從而，可得最大特征值λmax=2所對應的特征向量E1=(0.316 2 0.948 7)T，即本文所求的關于靜態剛度和模態一階固有頻率的加權因子。不失一般性，對于所求的特征向量中，非零特征向量數大于1時，為使權重因子的大小能更好地反映為相應目標函數的重要性，還需進行一致性判別處理。一致性指標(Consistency Index，CI)可表述如下：

(12)

式中：N為子目標數目；λmax為特征值數組中的最大特征值；JI為隨機產生矩陣的一致性指標[14]。當CJ<0.1時，則決策矩陣的一致性合格，依據決策矩陣所求的特征向量Ei即可作為多目標中各子目標的加權因子。本文依據特征向量E得到非零特征向量數為1，不需一致性判別。

依據特征向量E1，可得靜態剛度和模態一階固有頻率的加權因子比約為1∶3，即為0.25和0.75。

3.2 多目標優化的總目標函數

由于折衷規劃法的原理簡單易懂，在工程領域中的多目標規劃中具有較好的實用性，因此，本文主要采用折衷規劃法并結合對動態目標函數的平均頻率法，對式(6)和式(8)的兩個目標函數進行綜合，形成的總目標函數為：

(13)

式中：F(x)為多目標函數；ωc為柔度加權因子；ωm為一階固有頻率加權因子；cmax、cmin為罩殼的靜態柔度最大值、最小值；mmax、mmin為罩殼的模態一階固有頻率最大值、最小值。

綜上所述，結合發動機罩殼關于靜態柔度和模態一階固有頻率的單目標拓撲優化結果，式(13)可進行具體的數值化為：

(14)

式中：c為柔度變量；m為一階固有頻率變量。

然而，OptiStruct僅支持單目標的拓撲優化求解，對于多目標優化問題，需通過內嵌的函數編輯器進行多目標優化函數的編寫。由式(14)可得柔度折衷值與一階固有頻率折衷值的平方和的平方根，即多目標函數。本文采用OptiStruct中平方和平方根函數rss對該優化目標函數進行編輯，如圖5所示。

圖5 基于二次開發內嵌的多目標函數

圖5中F為關于柔度和一階固有頻率的多目標優化函數；c和m為多目標優化過程的柔度值和一階固有頻率，隨優化迭代而變化。

4 優化結果

4.1 靜態剛度優化結果

依據第1.1節中的汽車發動機罩殼的有限元模型和第1.2節中的工況條件，結合第2.2節中基于水平集法的優化數值模型，采用OptiStruct優化求解,相鄰迭代的優化目標絕對差值作為迭代終止條件，該容差值設置為0.005。經過18次優化迭代，得到靜態拓撲優化收斂后結構材料分布情況如圖6所示。

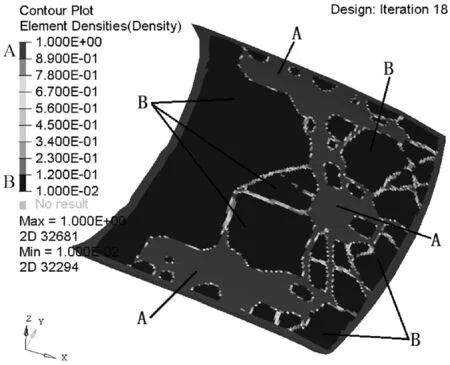
圖6 靜態拓撲優化結果

圖6中區域A的連續部分表明罩殼在該處為受外載影響的主要區域，需布置較厚的材料或布置加強筋；區域B的連續部分表明罩殼在該處為非受載區，可去除該連續區域內的材料或加強筋的布置。基于靜態拓撲優化后的發動機罩殼，其優化前后的剛度特性和整體質量等主要性能參數如表3所示。

表3 靜態拓撲優化前后的性能參數

發動機罩殼的靜態優化結果分析表明：發動機罩殼的柔度值從8.36 mm/N下降到了4.78 mm/N，下降了42.82%，表明發動機罩殼的剛度有了較大的提升；最大應力值從268.36 MPa，下降到238.36 MPa，表明結構的集中應力現象有了較大的改善，這也意味著發動機罩殼的結構力學性能有了明顯的改善。此外，發動機罩殼的質量由10.38 kg降到3.11 kg，說明發動機罩殼在改善結構性能的同時，還實現了結構的輕量化，節省結構制造的材料成本。

4.2 模態優化結果

依據發動機罩殼的有限元前處理模型及其工況條件，結合第2.3節中基于水平集法的動態優化數值模型，采用OptiStruct進行優化求解，相鄰迭代的優化目標絕對差值作為迭代終止條件，該容差值設置為0.005。經過27次的優化迭代，可得到動態拓撲優化收斂后的結構材料分布情況和優化迭代曲線如圖7所示。

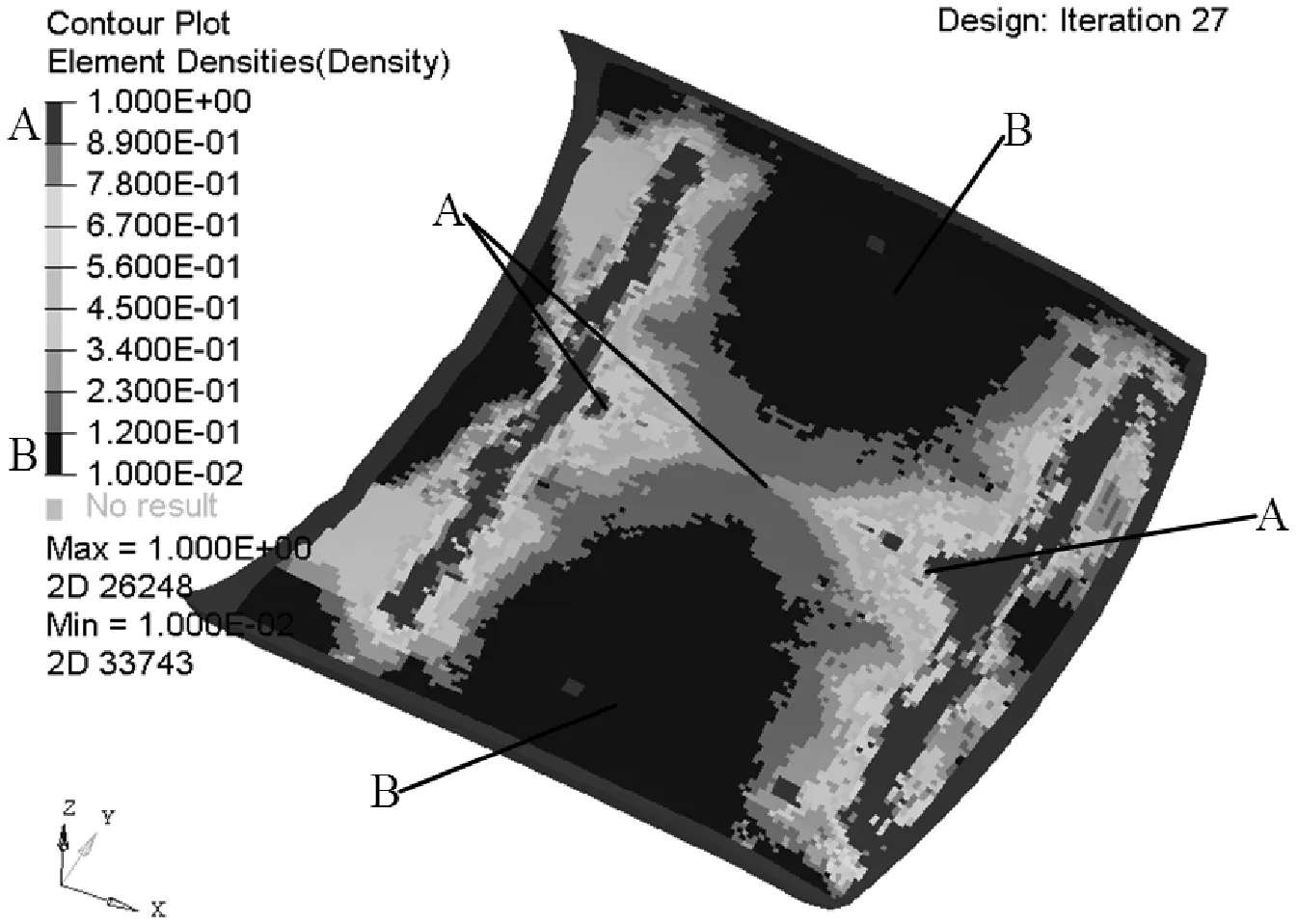
圖7 模態拓撲優化結果

圖7中區域A的連續部分表明罩殼在該處為受振動影響的主要區域，需布置較厚的材料或布置加強筋；區域B的連續部分表明在該處受振動的影響甚微，結構改進中該區域可不作改進設計。基于模態拓撲優化后的發動機罩殼，其優化前后的結構模態特性參數如表4所示。

表4 動態拓撲優化前后的性能參數

發動機罩殼的模態優化結果分析表明：發動機罩殼的一階固有頻率從368.698 Hz提高到了501.035 Hz，增強了35.89%，表明發動機罩殼的動態特性有了很大提升，其抑制振動能力也有了很大提升。

4.3 多目標優化結果

本文基于水平集法和多目標優化理論，構建以總目標函數最小化，以優化前后體積分數為約束條件的發動機罩殼的優化數值模型。相鄰迭代的優化目標絕對差值作為迭代終止條件，該容差值設置為0.005，采用OptiStruct進行40次求解，得到罩殼的優化結果和優化迭代曲線如圖8所示。

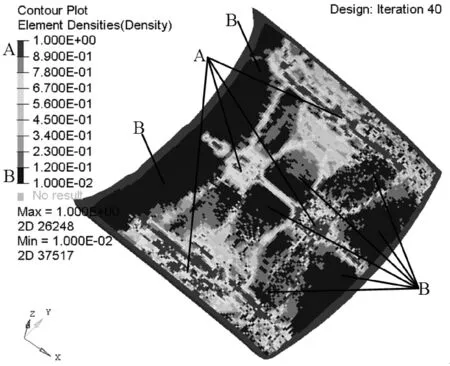
圖8 多目標優化結果

圖8中區域A的連續部分表明該處為罩殼受外載和振動影響的主要區域，需布置較厚的材料或布置加強筋；區域B的連續部分表明在該處受外載荷和振動的影響甚微，可去除該區域的加強筋布置。基于多目標優化后的發動機罩殼，其優化前后性能參數如表5所示。

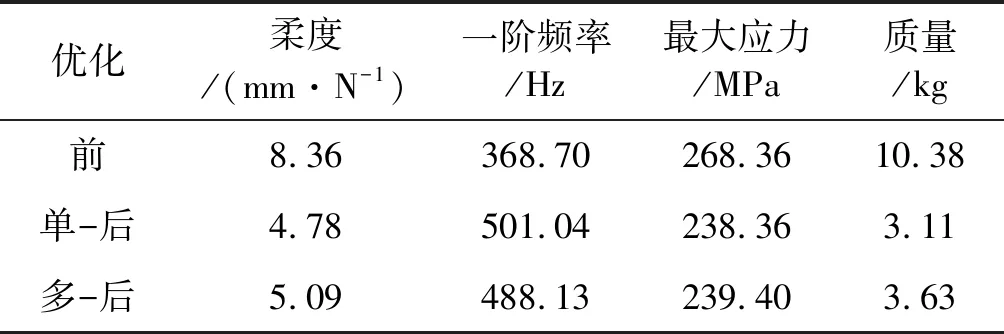
表5 多目標拓撲優化前后的性能參數

綜上所述，基于水平集法的多目標拓撲優化，所設計的發動機罩殼柔度值從8.36 mm/N下降到了5.09 mm/N，一階固有頻率從368.698 Hz提高到了488.129 Hz，表明罩殼的靜、動態結構特性明顯改善，增強了振動抑制能力。最大應力從268.36 MPa下降到239.40 MPa，處于罩殼材料許用屈服強度值范圍內。該設計有效地消除了結構集中應力現象，且實現了結構設計的輕量化。

5 結 語

本文在拓撲優化技術中引入了水平集方法并結合多目標理論，采用OptiStruct對發動機罩殼進行了多目標優化設計。通過優化前后的相關性能參數比較，結果表明：水平集拓撲優化技術能有效地提高罩殼的靜、動態結構性能，增強結構的振動抑制能力。基于層次分析法確定權重因子，避免了多目標優化模型構建中的主觀能動性。采用平均頻率法對動態目標函數的處理，有效地消除了動態優化過程中的收斂性。該方法為工程結構的多目標優化設計提供了理論設計方法和重大應用價值。此外，該技術還將數量統計知識引入到優化理論中，為相關算法的創新發展提供一定的借鑒作用。