最大度為5的哈密頓圖的星邊色數(shù)

王 瑩，申玉發(fā)，肖 宏，周 雪

(河北科技師范學(xué)院數(shù)學(xué)與信息科技學(xué)院，河北 秦皇島，066004)

圖的染色理論是圖論中很重要的研究課題。應(yīng)解決實(shí)際問題的需要，在經(jīng)典圖的頂點(diǎn)染色和邊染色的基礎(chǔ)之上，衍生出了一些帶有限制條件的邊染色問題，如圖的強(qiáng)邊染色和星邊染色等問題。

定義1[1]圖G的一個正常k-邊染色是指一個映射φ∶E(G)→{1,2,…,k}，且對E(G)中任意兩條相鄰的邊e1,e2都滿足φ(e1)≠φ(e2)。

以下介紹兩種有約束條件的邊染色的定義。

定義2[2]圖G的一個強(qiáng)k-邊染色是G的一個滿足任意兩條距離至多是2的邊染不同顏色的正常k-邊染色。若圖G有一個強(qiáng)k-邊染色，則稱G是強(qiáng)k-邊可染的。圖G的強(qiáng)邊色數(shù)是使G有一個強(qiáng)k-邊染色的最小非負(fù)整數(shù)k，用χs′(G)來表示。

定義3[2]圖G的一個星k-邊染色是G的一個滿足任意長度是4的路或圈至少用3種顏色染色的正常k-邊染色。若圖G有一個星k-邊染色，則稱G是星k-邊可染的。圖G的星邊色數(shù)是使得G有一個星k-邊染色的最小非負(fù)整數(shù)k，用χst′(G)來表示。

根據(jù)定義可知，圖G的星邊色數(shù)與強(qiáng)邊色數(shù)之間有如下關(guān)系式[2]：

χst′(G)≤χs′(G)

強(qiáng)邊染色的概念是Fouquet等[3]在1983年為解決無線電通信網(wǎng)絡(luò)中的信道分配問題而提出的。1989年，Erd?s等[4,5]提出了一個關(guān)于圖的強(qiáng)邊色數(shù)上界的猜想：對于任意的圖G，當(dāng)圖的最大度Δ為偶數(shù)時，有χs′(G)≤1.25Δ2；當(dāng)Δ為奇數(shù)時，有χs′(G)≤1.25Δ2-0.5Δ+0.25。之后，學(xué)者們圍繞著這個頗具挑戰(zhàn)性的猜想做了大量的研究工作，也取得了一系列的成果。2015年，Zang[6]證明了下面的引理。

引理1每個最大度是5的圖都是強(qiáng)37-邊可染色的。

由于到目前為止，關(guān)于最大度為5的圖的星邊色數(shù)的上界還沒有相關(guān)結(jié)果，因此想要確定這種圖的星邊色數(shù)，就只能借助上面的星邊色數(shù)與強(qiáng)邊色數(shù)的關(guān)系式和引理1，由此兩者可知，最大度為5的圖是星37-邊可染的。

星邊染色是劉信生等[7]在星點(diǎn)染色的基礎(chǔ)上于2008年定義的。同時，他們給出了一般圖的星邊色數(shù)的一個上界：若圖G是Δ≥7的簡單圖，則有χst′(G)≤[16(Δ-1)3/2]。因為星邊染色的概念比強(qiáng)邊染色概念的提出晚了20多年，所以人們目前對于星邊染色的研究并沒有強(qiáng)邊染色研究的深入，圍繞圖的星邊染色的結(jié)果相對較少。

2013年，Mohar等[8]研究了完全圖、子立方圖等的星邊色數(shù)，并證明了下面的引理。

引理2每個最大度為3的圖都是星7-邊可染色的。

2019年，王瑩[2]證明了最大度是4的圖都是星14-邊可染的。

本次研究主要圍繞圖的星邊染色問題展開，通過對圖的結(jié)構(gòu)進(jìn)行分析，再運(yùn)用邊分解的方法，證明每個最大度為5的哈密頓圖是星22-邊可染的。

首先，筆者給出證明中所用到的術(shù)語和定義。本次研究考慮的圖是有限簡單圖。設(shè)V(G)表示圖G的頂點(diǎn)集、E(G)表示G的邊集，而Δ(G)，δ(G)分別表示G最大度和最小度[9]。通常用u和v表示G中的兩個點(diǎn)，用e表示G中的一條邊，若e可以用等式e=uv表示，則稱點(diǎn)u和v是邊e的端點(diǎn)，也可以叫做u和v相鄰[2]。如果兩條邊與同一個點(diǎn)關(guān)聯(lián)，此時就把兩條邊叫做相鄰的。用NG(v)表示與點(diǎn)v相鄰的點(diǎn)集合，用dG(v)=|NG(v)|表示點(diǎn)v在G中的度。用dG(u,v)表示連接2個點(diǎn)u和v的最短路的長度，即它們在G中的距離。在不引起混淆的情況下，分別將Δ(G)，NG(v)，dG(v)，dG(u,v)簡記為Δ，N(v)，d(v)，d(u,v)。一個k-點(diǎn)是一個度數(shù)為k的點(diǎn)。對i≥1，用ni(v)表示與點(diǎn)v相鄰的i-點(diǎn)的個數(shù)。圖中兩條邊的距離是指對應(yīng)線圖中相應(yīng)兩點(diǎn)之間的距離。若兩條邊相鄰，則稱這兩條邊的距離為1。若兩條邊不相鄰，但這兩條邊有公共鄰邊，則稱這兩條邊的距離為2。

對于圖G的一個非空的邊集E′?E，通常用F-E′表示從G中刪去E′中所有的邊而得到的子圖[10]。G的一個由邊集E′導(dǎo)出的邊導(dǎo)出子圖G[E′]是以E′為邊集，以至少與E′中一條邊關(guān)聯(lián)的點(diǎn)的全體為點(diǎn)集的圖。

一個含圖G的每一個頂點(diǎn)的圈被稱為G的一個哈密頓(Hamilton)圈[1]。顯然，G的一個哈密頓圈是G的一個生成圈。一個含有哈密頓圈的圖稱為哈密頓圖[9]。由定義可知，圈Cn是哈密頓圖，完全圖Kn是哈密頓圖。

若將G分解成子圖G1,G2,…,Gm使得E(G)=E(G1)∪E(G2)∪…∪E(Gm)，且當(dāng)i≠j時，有E(Gi)∩E(Gj)=?，則稱其為圖G的一個邊分解。

以下筆者將重點(diǎn)研究最大度是5的哈密頓圖的星邊染色問題。

定理1若G是一個最大度為5的哈密頓圖，則有χst′(G)≤22。

證明設(shè)G是Δ(G)=5的哈密頓圖，根據(jù)定義可知G必是連通的。用G2表示G的一個哈密頓圈，顯然，G2?G。這樣，圖G中的邊就被分成了兩類：哈密頓圈上的邊和不在哈密頓圈上的邊(哈密頓圈的弦)。將不在哈密頓圈G2上的邊組成的集合的導(dǎo)出子圖記為G1，則有E(G)=E(G1)∪E(G2)，E(G1)∩E(G2)=?且Δ(G1)≤3。用C={1,2,…,22}表示一個顏色集合。按如下方法給出圖G的一個星22-邊染色φ。

步驟1用C1={1,2,…,7}中的7種顏色對G1中的邊進(jìn)行星邊染色。

根據(jù)引理2，由圖G1滿足Δ(G1)≤3，得G1是星7-邊可染的，因此，這個染色是可行的。

步驟2用C2={8,9,…,22}中的15種顏色對G2中的邊進(jìn)行星邊染色。

在這一步驟中，將用顏色集合C2對G2中的邊進(jìn)行貪婪染色。設(shè)|E(G2)|=n，對G2的邊按逆時針順序進(jìn)行如下標(biāo)號：e1,e2,…,en，并且將e1,e2,e3的頂點(diǎn)分別記為b,,a,c,d。為使敘述簡潔，在考慮對邊ei∈E(G2)，i=1,2,…,n，進(jìn)行染色時，將與ei距離為2的且有弦作為公共鄰邊的邊稱為ei的禁用邊，將ei的禁用邊上所染的顏色組成的集合記為F(ei)。e1′,e2′,e3′,e4′,e5′,e6′既是邊e1的禁用邊，也是邊e2的禁用邊(圖1)。因為，對于任意的邊ei至多有12條禁用邊，所以|F(ei)|≤12。

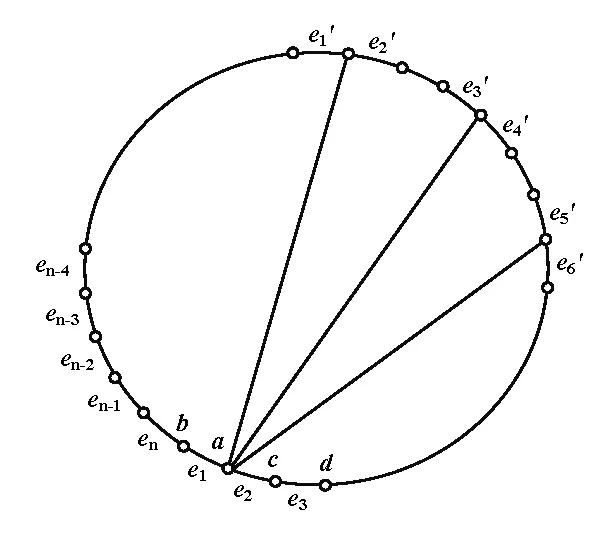
圖1 哈密頓圖

現(xiàn)在按角標(biāo)順序?qū)2中的邊進(jìn)行染色：

先染色邊e1，此時，由于e1的禁用邊都沒有染色，用顏色8來染e1，即φ(e1)=8。

再染色邊e2，只需回避e1所染的顏色，不妨用顏色9來染色邊e2，即φ(e2)=9。

再染色邊e3，只需回避e1和e2所染的顏色，不妨用顏色10來染e3，即φ(e3)=10。

…

再染色邊ei(4≤i≤n-2)時，只需回避|F(ei)∪φ(ei-1)∪φ(ei-2)|≤14種顏色，由|C2|=15，知邊ei可以染好。

再染色邊en-1，需回避|F(en-1)∪φ(en-2)∪φ(en-3)|≤14種顏色。

最后，染色邊en，根據(jù)φ(en-1)和φ(e1)是否相等分別進(jìn)行討論：

情況1φ(en-1)≠φ(e1)

染色邊en時，只需要回避|F(en)∪φ(en-1)∪φ(e1)|≤14種顏色，就可以得到圖G的一個星22-邊染色。

情況2φ(en-1)≠φ(e1)=8

令A(yù)=F(en)∪φ(en-2)∪φ(e1)∪φ(e2)=F(en)∪φ(en-2)∪{8,9}，根據(jù)在染色時邊en是否有可用色，分以下兩種情況進(jìn)行討論：

情況2.1A≠C2

用C2-A中的顏色染色邊en，就可以得到圖G的一個星22-邊染色。

情況2.2A=C2

此時|A|=15且集合中的任意兩條邊都染了不同顏色，再考慮是否可以改染邊e1：

情況2.2.1若F(e1)∪φ(e1)∪φ(e2)∪φ(e3)=F(e1)∪{8,9,10}≠C2，則可以用在C2中卻不在F(e1)∪{8,9,10}中的某顏色改染邊e1，改染后即回到情況1。

情況2.2.2若F(e1)∪{8,9,10}=C2，則|F(e1)∪{8,9,10}|=15，先用顏色10改染邊e1，并且將改染后的顏色記為φ′(e1)，再考慮如何染色邊en。若F(en)∪φ′(e1)∪φ(en-1)∪φ(e2)=F(en)∪{8,9,10}≠C2，此時，就回到了情況2.1。若F(en)∪{8,9,10}=C2=A，即φ(en-2)=10。此時，用顏色α∈C2-(F(e2)∪{9,10})改染邊e2，再將邊e1改染為9，即可回到情況1。

為了進(jìn)一步說明運(yùn)用以上方法得到的染色φ是圖G的一個星邊染色，下面運(yùn)用反證法來進(jìn)行證明。

假設(shè)圖G中有一條長度為4的路(或者圈)上的連續(xù)的4條邊分別染色為αβαβ，其中α,β∈C。根據(jù)以上方法制訂的染色規(guī)則，顏色α和β不能同時屬于集合C1或C2。不失一般性，不妨假設(shè)α∈C1，由距離為2的兩條禁用邊一定染不同染色，知β∈C2必不成立。證畢。

結(jié)論每個最大度為5的哈密頓圖都是星22-邊可染的。