不同應力幅值下大理巖受循環動力擾動的力學特性實驗研究

劉勇文，李 忠

(黃河水利職業技術學院，河南 開封 475004)

在實際工程中，尤其是地下開挖工程，巖石穩定性的破壞往往不是由靜荷載造成的，尤其是井下采礦，通常是動力擾動造成的，動力擾動除了外部機械、爆炸等造成的動力沖擊外，巖石開挖會導致其開挖體周圍的應力重新分布，頻繁的開挖活動會造成一定范圍內的巖石應力處于動態調整中，巖石內部應力的不斷變化也可以看成一種動力擾動現象[1-3]。在深部礦體開采中，由于地應力和上覆巖層重力的影響，開挖礦體通常處于高應力狀態，在頻繁的動力擾動作用下極易發生類似巖爆的巖體大面積破壞[4-6]。因此，揭示巖石在高靜應力狀態下受動力擾動的力學特性及破壞機制，對于防治礦山開采巖爆等巖體動力破壞有著重要意義。地下開采中，巖體受到的動力擾動主要表現為采場爆破、應力重分布、巖體破壞活動等，尤其是采場爆破，其產生的地震波對周邊巷道及礦柱穩定性影響極大，而這些地震波頻率低、傳播距離遠、攜帶能量大，因此，研究低頻動力擾動對巖體力學特性的影響更具有工程意義[7-10]。在巖石力學試驗中，可以通過對巖石試樣施加一定頻率的循環加卸載模擬巖石在井下開采過程中所處的動力擾動環境。由于受動力擾動如爆破、應力重分布作用形式的不同，其應力擾動的幅值也不同，在深井開采中，巖石處于高應力狀態，當受到較小的應力擾動時就可能導致巖石的應力超過其屈服應力，使巖石發生破壞，循環擾動與靜力作用的疊加作用可能導致巖石在應力未達到其破壞極限時也發生破壞[11-14]。由此可見，研究不同應力幅值下巖石受循環動力擾動的力學特性具有一定的工程意義。

1 試驗設備及方案

1.1 試驗設備及加載方法

本次試驗采用中南大學MTS-322電液伺服靜動萬能試驗機，該試驗機可實現頻率在0～20 Hz之間、荷載大小在0～500 kN之間的軸向循環擾動荷載。

試驗加載方法：首先，對大理巖試樣緩慢施加軸向靜荷載至某個數值(小于其單軸抗壓強度)，將該軸向靜荷載記為σm；以σm為軸向循環擾動荷載的平均值，施加固定頻率的軸向動荷載，直至試樣破壞或試驗結束。圖1為試驗加載過程示意圖，圖1中σmax為軸向擾動荷載的最大值，σmin為軸向擾動荷載的最小值，T為一個循環動荷載的加載周期。將擾動荷載的最大值和最小值的差值Δσ=σmax-σmin記為循環動力擾動幅值。本次試驗采用的循環擾動荷載為正弦波波形，其擾動頻率為5 Hz。

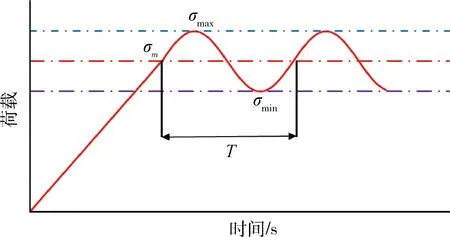
圖1 試驗加載過程示意圖Fig.1 Schematic of load wave of cycle loading

1.2 預加載試驗

本次試驗采用的大理巖試樣來自冬瓜山銅礦礦體頂板，通過對大理巖巖石試塊進行加工、打磨，制備成直徑為50 mm左右、高度為100 mm左右的標準巖石試樣。共加工8個試樣，試驗的基本參數見表1。其中，Dh1～Dh3為單軸壓縮試驗試樣；Dh4～Dh5為循環擾動預加載試驗試樣；Dh6～Dh8為循環擾動加載試驗試樣。

首先，通過單軸壓縮實驗獲取大理巖的主要靜力學參數，見表2。根據測得的單軸抗壓強度值，確定循環擾動試驗σm的數值，σm的數值盡量靠近大理巖彈性段極限，以模擬巖石的高應力狀態。σmax和σmin的選取是本次試驗的關鍵，為了獲取合適的σmax和σmin，循環擾動試驗之前開展了2次預加載試驗，掌握大理巖在循環擾動荷載作用下所能承受的應力幅值。最終確定的循環擾動試驗方案見表3，表3中的上限應力比為軸向擾動荷載的最大值與單軸抗壓強度的比值，下限應力比為軸向擾動荷載的最小值與單軸抗壓強度的比值，平均應力比為軸向循環擾動荷載的平均值與單軸抗壓強度的比值。

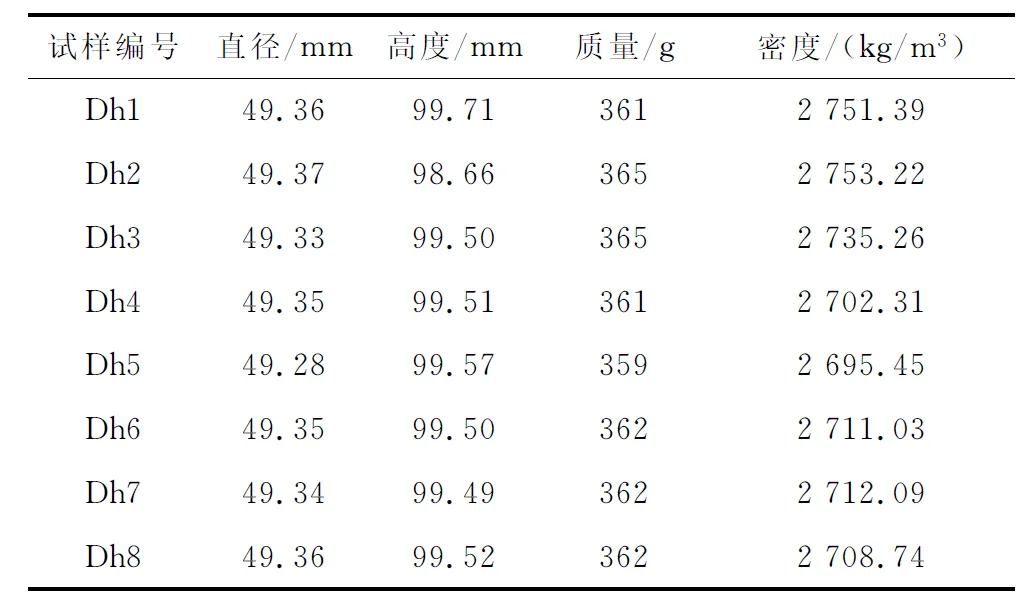
表1 試樣基本參數Table 1 Parameters of sample

表2 靜力學參數Table 2 The statics parameters

表3 循環動力擾動力學試驗方案Table 3 Scheme of mechanics experiment under circle dynamic disturbance

2 試驗結果與分析

由表3可知，試驗過程中，首先對試樣軸向施加荷載，緩慢加載至預定軸向應力σm，然后按照試驗確定的循環擾動試驗方案，施加以Δσ為應力幅值的循環擾動荷載，擾動頻率為5 Hz。試驗過程中，如果試樣在受到多次循環擾動荷載作用后(1 000次)仍然不發生破壞，說明在該應力幅值下，巖石在循環擾動作用下不會發生破壞，此時，保持σmin不變，每次增加σmax的數值為5 MPa，繼續進行循環擾動試驗，直至試樣發生破壞。

2.1 低應力幅值下的彈模強化

圖2為試樣Dh6在不同應力幅值下其循環擾動次數與軸向累積應變之間的關系曲線。由于試樣Dh6的初始循環擾動應力幅值較小，循環擾動加載1 000次后，試樣仍未發生破壞，軸向擾動荷載的最大值σmax=95 MPa，在加載初期，軸向應變很快增加至0.34%，隨著循環加載次數的增加其軸向應變不發生變化；隨后增加軸向擾動荷載的最大值σmax=100 MPa，在加載初期軸向應變值很快增加至0.42%，隨著循環加載次數的增加其軸向應變依然未發生變化；將軸向擾動荷載的最大值σmax增加至110 MPa，循環擾動加載267次后，試樣發生破壞。

試驗表明，在低頻循環擾動荷載試驗條件下，當應力幅值Δσ較低時，即使循環加載多次(1 000次)，試樣軸向應變值不發生變化，試樣不發生破壞，說明在循環擾動加載試驗中，存在軸向擾動荷載門檻值，只有當軸向擾動荷載最大值超過門檻值，試樣才會發生破壞。當軸向擾動荷載的最大值小于門檻值時，隨著σmax的增大，出現彈性模量強化現象，試樣Dh6在軸向擾動荷載最大值為110 MPa時的彈模比95 MPa時提高了42%。主要原因是在循環加載過程中，當軸向擾動荷載最大值較小時，巖石試樣內部的空隙、裂紋在循環擾動荷載作用下被壓密、閉合，巖石剛度增加，從而造成試樣的彈模提高。

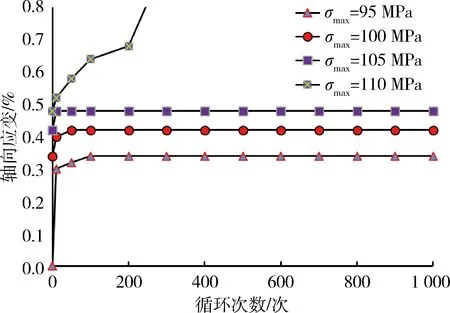
圖2 Dh6循環擾動次數與軸向累積應變關系曲線Fig.2 The corresponding relationship of cycle numbers and cumulative strain of Dh6

2.2 不同動力擾動幅值下試樣的破壞形態

圖3為大理巖試樣在不同循環擾動應力幅值下的破壞形態。在逐級加載和應力幅值為60 MPa條件下，試樣表現為單剪切面破壞，當循環擾動應力幅值增加至90 MPa時，試樣局部出現了碎裂、彈射，軸向裂紋的數量明顯增多，循環擾動應力幅值的大小對大理巖試樣的破壞形態有較為顯著的影響.

圖3 不同循環擾動應力幅值下大理巖試樣的破壞形態Fig.3 The damage model of marble specimens under different dynamic disturbance amplitudes

3 損傷模型

巖石在不同循環動力擾動幅值下的破壞可以看做是巖石內部在循環荷載持續作用下逐漸損傷的過程，因此，為了解釋巖石在循環動力擾動作用下的損傷演化規律，引入損傷變量對其損傷演化規律進行研究，根據以往研究，巖石在單軸壓縮條件下的損傷方程見式(1)[15]。

σ=εE(1-D)

(1)

式中：σ為應力，MPa；ε為應變；E為巖石在無損傷時的彈模，MPa；D為損傷變量。

巖石在循環擾動的加載條件下，其應力幅值Δσ在循環加載過程中數值保持不變，為了便于研究，將式(1)中的σ由Δσ替代，建立循環動力擾動作用下損傷變量方程見式(2)。

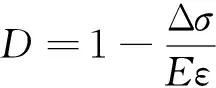
(2)

對式(2)兩邊同時求導，可得式(3)。

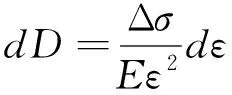
(3)

對式(3)兩邊同時進行積分，可得式(4)。

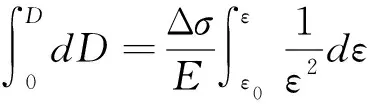
(4)

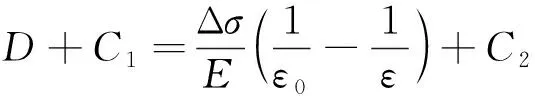
(5)

式中：ε0為施加軸向靜荷載結束時的軸向應變；εd為試樣發生整體破壞時軸向最大應變；C1、C2為積分常數。

由式(5)可知，C1、C2為積分常數，只要求得C1、C2，便可建立損傷變量D與應變之間的演化方程。帶入邊界條件D=0，此時有ε0=ε，帶入式(5)可得C1=C2，公式兩邊可以消掉。當D=1時，試樣發生破壞，此時ε=εd，帶入式(5)，可得式(6)。

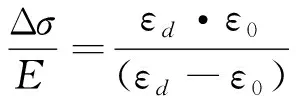
(6)

將式(6)和C1=C2帶入式(5)，可得式(7)。

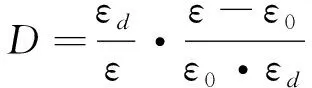
(7)

循環動力擾動試驗中，根據試驗過程中的應力-應變試驗數據，可以直接獲得施加軸向靜荷載結束時的軸向應變ε0和試樣發生整體破壞時軸向最大應變εd，將每個應力擾動循環的軸向擾動荷載的最大值σmax對應的ε帶入式(7)，可計算求得每個應力擾動循環的累積損傷值D。

圖4為大理巖在60 MPa和90 MPa動力擾動應力幅值條件下每個循環根據式(7)計算的損傷變量值與循環次數之間的對應關系。從圖4中可以看出，在動力擾動應力幅值為60 MPa時，損傷變量隨循環次數的增加基本可劃分為三個階段：迅速增長階段、平穩發展階段和快速增長階段。隨著動力擾動應力幅值從60 MPa提高至90 MPa，以及循環次數的增長，損傷變量迅速增長，試樣發生破壞，增大動力擾動幅值對巖石試樣的損傷影響顯著。

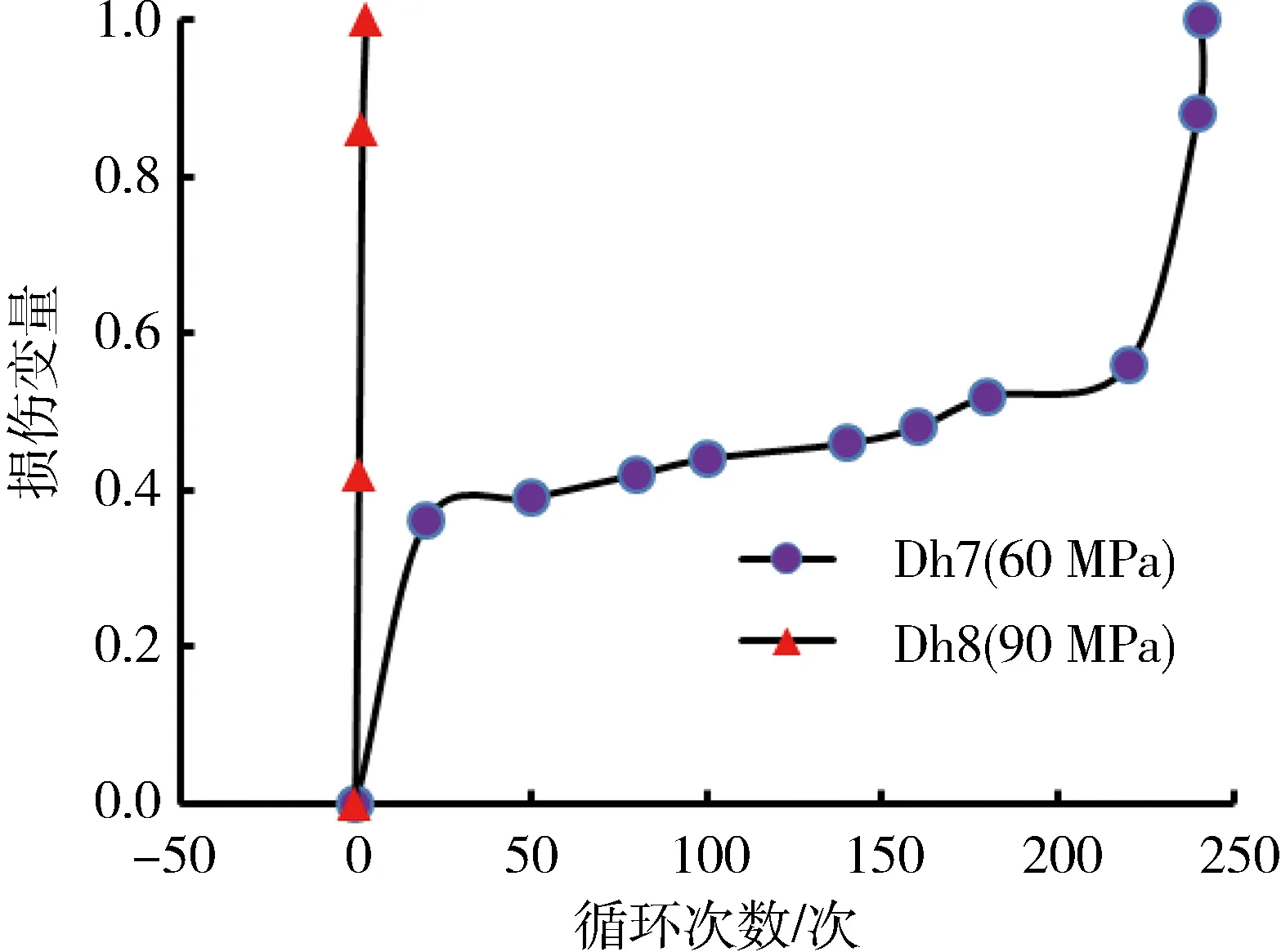
圖4 循環擾動次數與損傷變量的關系Fig.4 The relation of cycle numbers and damage variable

4 結 論

1) 巖石試樣在低頻循環動力擾動作用下，其應力擾動幅值對巖石試樣的力學特性影響顯著，應力幅值較小時，試樣雖經多次循環擾動但未發生破壞，隨著應力幅值的提高，試樣破壞時的累積循環擾動次數減少。

2) 逐級加載過程中，試樣出現了彈模強化現象，即隨著軸向擾動荷載的最大值σmax的提高，試樣的彈性模量也隨之增大。

3) 建立了循環動力擾動作用下的應變損傷模型，對循環動力擾動作用下巖石試樣的損傷規律進行了研究，增大動力擾動幅值對巖石試樣的損傷影響顯著。