例題教學中的“變臉”藝術
姚敏
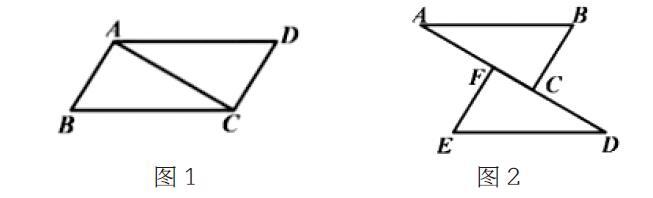
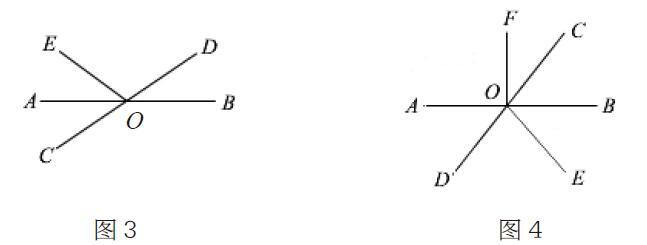
【摘 要】 本文首先分析出例題教學中的“變臉”藝術,包括圖形的“變臉”、條件的“變臉”、解法的“變臉”、結論的“變臉”,最后分析初中數學教學中“變臉藝術”的應用,有利于提高課堂教學的有效性,在對數學問題的解決中運用“變臉”藝術,將抽象的數學知識變換為直觀的事物呈現出來,從多個角度培養學生的思維,加深學生對數學知識的理解與掌握,提高學生的數學學習能力和數學素養。
【關鍵詞】 例題教學;變臉藝術;有效性
伴隨著新課改的不斷深入,開始重視課堂教學的有效性。初中數學教師在課堂教學中運用變式教學,將抽象的數學知識變換為直觀的事物呈現出來,從多個角度培養學生的思維,加深學生對數學知識的理解與掌握,提高學生的解題應變能力。在例題教學中的變臉藝術可以避免題海,激發學生的學習興趣,有利于學生鞏固數學知識,培養學生的獨立思考能力,提高學生的數學學習能力,增強數學課堂教學的有效性。
一、圖形的“變臉”
在初中數學課堂教學中,運用變式教學,通過圖形的變化來培養學生的探究能力和識圖能力。學生根據圖形可以加深對數學知識的理解,激發思維,開展創造性思維,提高解決問題的能力,從而提高數學課堂的有效性。例如在人教版八年級上冊《三角形全等的判定》的教學中,數學教師要讓學生經歷探索三角形全等條件的過程,記住全等三角形的判定方法(SSS),學會運用該方法判斷三角形是否全等。
例題:如圖1,已知AB∥BE,AB=DE,AF=CD,求證BC=EF。
本題是一個幾何中三角形的證明題,根據變式將△ADC上移,得到圖2,從而得出BC=EF。
根據圖形的“變臉”,使學生感受到學習數學的樂趣,提高學生的學習熱情。
二、條件的“變臉”
在初中數學教學中應用變式教學,通過條件變化來變換題目,將數學中的知識有效結合,揭示問題的本質,這樣學生在不斷的變化中來發現數學的規律,培養學生的探索能力和想象能力,開拓學生的思維,激發學生的求知欲望,提高學生分析問題、解決問題的能力,從而提高初中數學課堂教學的有效性。例如在人教版初中數學七年級下冊《相交線》的教學中,數學教師要讓學生了解鄰補角、對頂角,能找出圖形中的一個角的鄰補角和對頂角,理解對頂角相等以及對頂角的性質與應用,運用它解決一些簡單的問題。
例題:如圖3,直線AB,CD相交于點O,∠EOC=70°,OA平分∠EOC,求∠BOD的度數(35°)。本題是一道有關相交線的證明題,對它的條件進行變式拓展,可以變換為如下題目:如圖4,已知直線AB,CD相交于點O,OE平分∠COD,FO⊥AB,∠EOF=120°,求∠AOD的度數(30°)。
通過問題中條件的互換來拓寬學生的解題思路,提高學生的解題能力。
三、解法的“變臉”
在初中數學教學中應用變式教學,提高課堂教學的有效性。由于數學問題具有抽象性和綜合多樣性,因此數學教師應該從多角度、多方位來引導學生去探索,得到不同的解法,培養學生的創新意識和探索精神,發散學生的思維,加強新舊知識的有效結合,提高學生分析問題、解決問題的能力。
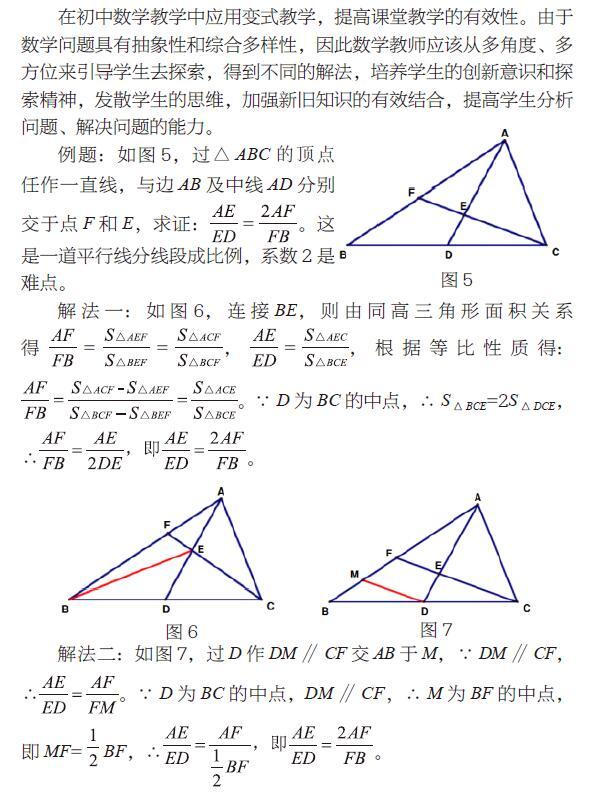
例題:如圖5,過△ABC的頂點任作一直線,與邊AB及中線AD分別交于點F和E,求證:=。這是一道平行線分線段成比例,系數2是難點。
解法一:如圖6,連接BE,則由同高三角形面積關系得==,=,根據等比性質得:。∵D為BC的中點,∴S△BCE=2S△DCE,∴。
解法二:如圖7,過D作DM∥CF交AB于M,∵DM∥CF,∴。∵D為BC的中點,DM∥CF,∴M為BF的中點,即MF=BF,∴。
四、結論的“變臉”
在初中數學教學中應用變式教學,在原題的條件下將結論進行擴展,培養學生的觀察能力,豐富學生的想象力,加深學生對數學知識的鞏固和延伸,提高學生的數學應變能力,提高學生的解題速率。例如在人教版九年級上冊《圖形的旋轉》的教學中。數學教師要讓學生感受旋轉與生活的緊密聯系,體會數學的應用價值,學生能根據自己的操作畫出旋轉前后的圖形,歸納出旋轉的性質,利用旋轉來解決問題。因此數學教師通過舉例來使學生初步感受旋轉,比如鐘表的時針運動,學生能總結圖形都圍繞某一定點轉動,也可以歸納出鐘表順時針方向、角度等關鍵詞,總結圖形旋轉的定義,從而幫助學生將知識系統化、牢固化,并達到一種檢驗的目的,培養學生的分析比較能力,增強學生的歸納總結能力和表達能力,使學生鞏固應用所學新知,培養學生的解題能力,提高學生的數學學習能力,進而提高初中數學課堂教學的有效性。
綜上所述,初中數學教學中“變臉藝術”的應用,有利于提高課堂教學的有效性。通過數學教師豐富多樣的教學手段,在對數學問題的解決中運用“變臉”藝術,將抽象的數學知識變換為直觀的事物呈現出來,從多個角度培養學生的思維,加深學生對數學知識的理解與掌握,提高學生的解題應變能力。“變臉藝術”在初中數學教學中的應用,幫助學生將知識系統化、牢固化,提高學生的數學學習能力,拓寬學生的解題思路,使學生感受到學習數學的樂趣,提高學生的學習熱情,逐漸培養學生的創新意識和探索精神,提高學生的數學素養。
【參考文獻】
[1]孫虎.欲問還休——從教材的“變臉”說起[J].數學學習與研究:教研版,2017.
[2]于文嵩.論初中數學課堂合作學習有效性教學策略分析[J].讀與寫(教育教學刊),2019,16(04):79.
[3]張惠.發展數學思維,展現課堂風采——論初中數學有效性教學策略[J].學周刊,2018(20):119-120.

