基于社會網絡分析的山地公園空間結構與布局優化

石亞靈

黃 勇*

肖 亮

城市公園作為市民體育、社交、休憩等活動的物質載體與空間場所，具有調節身心健康、促進社會經濟等益處[1-2]，其空間結構也是城鄉規劃和風景園林學科的重要研究領域[3-4]。回溯公共空間的相關研究，大致呈現3種態勢：1)公共空間系統的理論構建，集中于對城市形態學[5]、景觀生態學[6]和歷史人文[7]等領域的認知；2)公共空間規劃標準[8]和規劃方法[9]等建設經驗的總結與探討；3)公共空間與人的需求的互動評價分析[10]。三者均屬“質性”研究與“屬性”分析。而有關公園的研究成果則集中于理論構建、規劃設計和方法技術等方面[11]。理論構建方面，黃灝峰[12]、王連勇[13]等分別結合各類公園更新改造以及規劃設計過程中的相關問題進行了人性化、精細化等設計理念與實踐的歸納研究。規劃設計方面，Oguz認為城市公園的更新改造要考慮使用者的需求[14]；Chandier以美國天際線公園更新改造為例，探討保留場地原有特色及功能轉換等問題[15]；Ulam對美國城市公園內的使用人群進行了分析研究[16]；Babey等認為公園的安全使用須與青少年群體健康活動相結合[17]；Poudyal等分析了美國城市公園的用地規模[18]；毛小崗著重探討了北京城市公園2000—2010年的空間格局變化[19]；馮悅怡探討了城市公園景觀空間結構對其熱環境效應的影響[20]；姚雪松等結合老年人活動需求對城市公園供給進行評價[21]。方法技術方面，對于公園空間的定量研究日益增多，除了傳統的主成分分析法、結構方程模型、層次分析法等，空間句法、GIS等空間網絡分析技術地位日益凸顯[22]，空間句法等多關注空間物質形態的結構分析，忽略了物質形態背后人的行為主體作用，GIS更側重于分析對象的空間位置、分布和形態，不具備具象可操作的空間優化更新方式。得益于這些研究與實踐，許多公共品質低下的公園得到了及時的更新改造。然而，在我國快速推進的城鎮化建設背景下，目前仍有大量公園空間被破壞與廢棄，仍然避免不了公園空間存在的空間分布失衡、空間層級不明確和空間結構不完善等問題。

而山地城鎮區別于平原或其他地區的核心差異在于山地地表結構所產生的“地下-地面-空中”三維空間。基于這些地形起伏、用地受限和空間阻隔等原因特性，其公園空間存在的活力低下、功能混雜、結構破碎化等問題更加顯著。因此，為探討公園空間結構的合理性并進行優化，本研究擬采用社會網絡分析方法，從關系視角整合空間與社會研究，結合重慶山地公園具體案例，將公園空間作為點，通過人的作用使空間進行連通的關系作為線，選取網絡密度、平均距離、Lambda集合、k-核、中心勢等指標，綜合衡量公園結構的完備性、穩定性和層級性問題，深入解讀定量計算指標背后的社會與規劃含義，尋求解決公園空間問題的優化策略。

1 研究方法

1.1 整體思路

本研究以系統的思想對公園空間規劃建設進行思考，從公共空間網絡的完備性、穩定性、層級性[23]三方面對公園空間結構、空間層級、空間分布進行分析。公共空間的完備性是確保公共活動有效開展的前提，穩定性是豐富公共空間活動的有效保證，層級性是促進公共空間活力的強勁動力，其實質都是促進公共空間系統的內部聯系，增強系統的結構優化與功能穩定，最終實現公共空間網絡的完善。完備性要求評價空間的有序分布決定空間系統內部各要素是否協同運作；層級性要求公共空間系統內部各個空間的功能層級能互相配合和支持；穩定性促進了公共空間結構的完備性和網絡化，穩定性高則結構更加完整，可激發公共空間活力。

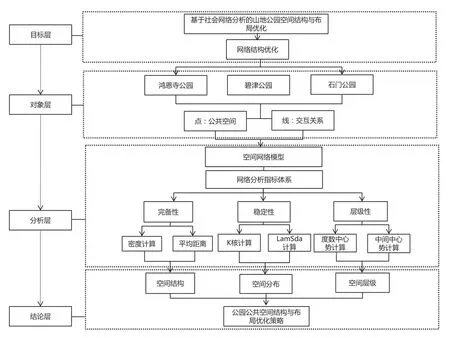
圖1 研究思路框架

整體研究思路分為4個步驟(圖1)：1)通過現狀調研，確定公園空間節“點”與交互關系“線”，對公園空間的人群活動路徑進行分析；2)基于公園空間交互關系的調研數據，構建社會網絡模型；3)從完備性、穩定性和層級性三方面構建公共空間網絡結構評價體系，包括網絡密度、平均距離、k-核、Lambda集合、中心勢等指標，其中，完備性指公園空間網絡結構關系的緊密程度與可達性，穩定性指公園空間網絡結構的活動有效性與活力度，層級性指公園空間網絡結構的點線面層級結構性；4)特征規律總結與規劃優化。其中，“社會網絡分析方法”是整體技術路線中的關鍵技術方法，結構指標體系是對公園空間網絡進行量化評價的關鍵技術環節。

1.2 研究對象與數據獲取

1.2.1 研究對象

鴻恩寺公園地處重慶市江北區龍脊山，面積約1 100畝(約0.73km2)，公園內地形地貌環境復雜。活動場地主要有主入口廣場、次入口廣場、觀景平臺、山脊中心廣場、東坡休閑廣場、山脊休閑廣場、休閑草坪、跌水場地、山頂廣場鴻恩閣和觀景廣場等，主要活動場地由位于山脊之上的公園主路串聯，道路呈魚排狀(圖2-1)。碧津公園位于重慶市渝北區兩路城中心，面積200余畝(約0.13km2)。公園山地環境特征明顯，是集休閑、娛樂、健身為一體的免費開放的綜合性文化休閑公園。活動場地主要有西側的兒童游樂場、北部的碧津湖沿岸休閑活動場地群、西側主入口及附近休閑活動場地、中部登山活動場地、門球運動場、南部博物館、跌水休閑場地和龍舌湖沿岸休閑活動場地群(圖2-2)。石門公園位于重慶市江北區石門北橋頭，面積144畝(約0.096km2)，地形呈馬蹄形。活動場地主要有主入口廣場、網球場、中心廣場、陽光草坪、游泳廣場、林間休息場地、兒童活動場和沿湖休閑場地等。公園內北側和西側的活動場地通過公園主要道路串聯，而公園南側和東側的活動場地由次要道路連接，呈樹枝狀(圖2-3)。

1.2.2 數據來源

圖2 研究靶區主要公共空間分布(2-1 鴻恩寺公園；2-2 碧津公園；2-3 石門公園)(底圖引自91衛圖)

數據收集分為調研觀察與調查問卷兩部分。調研觀察部分，分別對鴻恩寺公園、碧津公園與石門公園內游人的日常活動進行觀察記錄。結果顯示3個公園的休閑活動、文化娛樂活動、觀賞游覽活動、兒童活動和運動健身活動等均集中在4個時間段：早晨(6：00—8：00)、上午(9：00—11：00)、下午(15：00—17：00)及傍晚(19：00—21：00)。早晨時段，游人在公園內以登山、鍛煉、慢跑等健身活動為主；上午時段，健身活動人數逐漸增加，休閑活動人數減少，且以文化娛樂活動為主，如唱歌、跳舞等；下午時段，隨著公園內游人數量的增加，活動類型更為豐富，包括游樂場游覽、民俗文化展覽館觀賞等；傍晚時段，游人數量逐漸減少，公園內游人多進行健身、休閑和文化活動，但參與人數不及白天時多。公園4個時間段內各類活動人數如圖3所示。問卷部分，首先對公園內的公共空間節點進行歸類與編號，并對居民出行的行為路徑進行評價；其次，針對使用公園空間的不同人群，以訪談和問卷的方式對公共空間使用情況展開調查，將支撐居民戶外活動的完整性和連續性所需要或涉及的不同公共空間視作一個集合，并按活動展開的先后順序將集合內的公共空間節點用連線的方式表達出來，同時注明不同居民戶外活動經過的各種公共空間類型。

1.3 研究方法與指標體系

1.3.1 研究方法

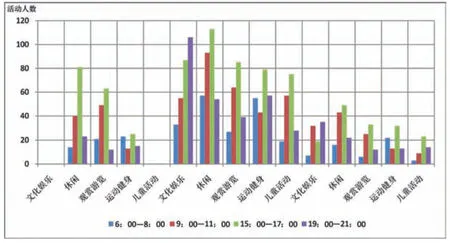
圖3 研究對象公園各時段活動人數

社會網絡理論與方法的發展歷程，大致可分為圖論、統計概率論的p1模型，以及代數理論的p＊模型3個階段。大多社會網絡可看作是對相似性、社會關系、相互作用和相互影響4種基本類型的研究[24]。社會網絡分析(Social Network Analysis，SNA)指標主要包括點、線與密度、中心度與中心性等。社會網絡擁有較長發展歷史和應用階段。在20世紀30年代，社會網絡是一種引用圖形表示個人主觀感受的技術。到了40年代，社會網絡在諸如“小世界”問題和“六度分離理論”等幾個前沿方向有所發展，在此期間，網絡分析也被社會學家用于研究城市社會結構變化[25]。60年代，網絡視角在人類學中蓬勃發展。70年代，網絡研究重心轉移到了社會學領域。80年代，伴隨著專業組織(International Network for Social Network Analysis，INSNA)的建立、會議(Sunbelt)的召開，軟件的應用(e.g.UCINET)以及期刊(Social Networks)的開辦，社會網絡分析已經成為社會科學的一個既定領域[26]。90年代，網絡分析輻射到物理學和生物學等領域，同時也應用于管理咨詢[27]、公共衛生[28]和犯罪/戰爭[29]等研究方向。21世紀，社會網絡分析的應用更為廣泛，如與旅游[30]、醫學[31]和生態學[32]相結合。近年來，社會網絡分析方法交叉融貫于城鄉規劃學的歷史街區保護[33]等微觀尺度、城鎮交通空間組織趨勢[34]等中觀尺度，以及城鎮群空間層級結構[35]等相關研究。

社會網絡模型由“點”和“線”組成，“點”是指現實社會中存在的行動實體，如個體的人、城市、街區或建筑等；“線”是指社會實體之間的相互關系或作用，如人與人的血緣關系、城市與城市之間的交通聯系等。本研究借助SNA將居民戶外活動視為一個完整的系統，將居民在戶外活動中所停留的公共空間視為節點，將所有問卷與訪談居民出行經過的公共空間節點的行為路徑進行疊加，選取主要人流連線，視作公共空間節點之間的連線，不僅能擺脫從個體出發研究屬性特征的弊端，從人與人的關系視角出發看待公園空間特征，而且能將人與人在空間中的活動通過網絡模型可視化。借助Ucinet 6.0軟件平臺，將整理的數據輸入，構建社會網絡模型。

1.3.2 指標體系

基于對社會網絡的分析以及公園完備性、穩定性和層級性等特征的綜合考量，綜合選取反映公園空間完備性的網絡密度和平均距離2項指標，反映空間穩定性的Lambda集合、k-核2項指標，以及反映空間層級性的度數中心勢和中間中心勢指標。

1)網絡密度。

一個網絡圖的密度定義為圖中實際擁有的連接數與最多可能擁有的線數之比，網絡密度公式可以測定網絡整體完備程度，計算公式為：

P=L/[n(n-1)/2]

式中，P為網絡密度，L為網絡中實際存在的連接數，n為網絡中實際存在的節點數。

2)平均距離。

任意2個節點之間距離的平均值，計算公式為：

L=2/n(n-1)[36]

式中，L為網絡中實際存在的連接數，n為網絡中實際存在的節點數。

3)Lambda集合。

通過分析網絡層級的邊關聯度，衡量網絡結構的整體穩定性。

4)k-核。

k-核(k=1、2、3……)計算可衡量網絡的局部穩定度，k值越高則占比越大，具有穩定結構的局部網絡成分越多，網絡整體越穩定。

5)度數中心勢。

能分析網絡整體的度數中心性，測試關系在網絡結構中的整體均衡程度，計算公式為：

式中，Cmax為網絡中各節點度數中心度的最大值，Ci為節點i的中心度。

圖4 網絡結構模型(4-1 鴻恩寺公園；4-2 碧津公園；4-3 石門公園)

6)中間中心勢。

可衡量一個節點在多大程度上位于其他任意2個節點的“中間”，計算公式為：

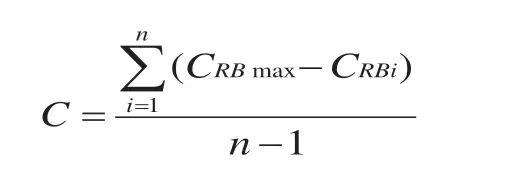
式中，CRBmax為點的絕對中間中心度理論最大值，CRBi為點的絕對中間中心度，C為點的相對中間中心度。

2 分析結果

2.1 拓撲結構與特征

圖4為鴻恩寺公園、碧津公園和石門公園的網絡拓撲結構。其中，鴻恩寺公園(圖4-1)呈現較為均質的環狀樹枝結構形態，結構中大部分空間節點存在多個聯系且與其他鄰近空間節點的關系較緊密，僅有H11、H19等空間節點由于空間地理位置稍遠而與其他節點關系偏弱，無孤立空間節點，整體關系表現比較集中緊湊；碧津公園(圖4-2)呈環狀形態，無孤立空間節點，整體關系比較緊密；石門公園(圖4-3)呈環狀結構形態，由于地形分割原因，空間關系表現出空間節點之間的相鄰可達關系，整體關系較緊密。

2.2 計算結果

2.2.1 網絡密度與平均距離

鴻恩寺公園、碧津公園和石門公園網絡結構的網絡密度計算結果分別為0.247 3、0.199 8、0.206 1，網絡結構的平均距離計算結果分別為1.873、1.907、1.970。

2.2.2 Lambda集合與k-核

Lambda集合分別計算各網絡的一級邊關聯度與最高級邊關聯度的比例差值，其中鴻恩寺公園共10層級，差值為0.903 2，網絡層級穩定性較好；碧津公園共13層級，差值為0.961 5，網絡層級穩定性較好；石門公園共13層級，差值為0.955 6，網絡層級穩定性較好。鴻恩寺公園網絡結構中，“5-核”比例為0.871 0，穩定性較弱；碧津公園網絡結構中，“5-核”比例為1.0，穩定性較好；石門公園社會網絡結構中，“5-核”比例為0.977 8，穩定性居中。

2.2.3 度數中心勢與中間中心勢

鴻恩寺公園網絡結構度數中心勢表現出以H2/H21號空間節點為中心的趨勢，比例為0.198 9；碧津公園網絡結構以B3/B5/B1空間節點為度數較大值的中心勢，比例為0.200 0；石門公園網絡結構中心趨勢比較集中和均衡，整體中心勢較低，比例為0.019 3。鴻恩寺公園網絡結構中間中心勢也表現出以H2/H21號空間節點為中心的趨勢，比例為0.070 6；碧津公園網絡結構表現出以B3/B5空間節點為中間值較大的中心勢，比例為0.047 4；石門公園網絡結構集中以S3/S6/S1空間節點中間值為最大，整體的中心勢較低，比例為0.053 7。

2.3 對比分析

通過對研究靶區網絡密度、平均距離、Lambda集合、k-核、度數中心勢、中間中心勢的分析，分別對其整體完備度、層級關聯度、局部穩定度、結構均衡性和集中趨勢進行對比分析(圖5)。由網絡密度與平均距離分析曲線可知，鴻恩寺公園的網絡密度最高，為0.247 3，碧津公園與石門公園較接近，排序為碧津公園＜石門公園＜鴻恩寺公園，平均距離排序為鴻恩寺公園＜碧津公園＜石門公園，故鴻恩寺公園的空間網絡結構最完備；由網絡層級關聯度差值曲線可知，鴻恩寺的差值最小，為0.903 2，碧津公園與石門公園接近，排序為鴻恩寺公園＜石門公園＜碧津公園，由網絡5-核比例分析曲線可知，碧津公園的比例最大，為1.000 0，鴻恩寺公園比例最小，為0.871 0，排序為鴻恩寺公園＜石門公園＜碧津公園，故碧津公園的網絡最穩定，鴻恩寺公園的網絡最不穩定；由網絡度數中心勢與中間中心勢分析曲線可知，鴻恩寺公園與碧津公園中心勢值接近，石門公園中心勢值較低，故鴻恩寺公園與碧津公園的網絡層級性較高，石門公園的層級性較低。

對各公園空間結構網絡值進行線性與對數歸一化處理(圖6)，分別得到計算公式：

鴻恩寺y=0.169x+0.100、y=0.564ln(x)+ 0.075

碧津公園y=0.167x+0.134、y= 0.576ln(x)+ 0.087

石門公園y=0.188x+0.037、y= 0.622ln(x)+ 0.014

3 討論

3.1 結構特征

3.1.1 地形影響空間網絡結構形態

基于公園空間節點聯系構建出的網絡模型主要表現為向心性(環狀)與蜂窩狀2種結構形態。在山地地形相對平緩、環境要素相對單一的碧津公園，空間關系較集中，網絡結構呈現環狀向心性趨勢，表現為以某一公共空間或幾個空間節點為核心的網絡結構形態特征(圖4-2)，由對比分析可知其整體網絡穩定性更好；而山地地形較為突出和復雜的鴻恩寺公園，空間關系較為分散，其網絡結構呈松散的環狀分布，表現為以多戶居民為核心的組團式結構形態特征(圖4-1)，由對比分析可知其整體網絡層級性較好；而在地形介于平緩與復雜之間的石門公園，其網絡結構呈現較為均衡的環狀，其完備性、穩定性和層級性均介于前二者之間。對比結果也在一定程度上反映出，集中型環狀網絡的結構穩定性和完備性都相對更好。因此可知，山地地形對公園空間網絡的構建與形成有著一定程度的影響。

3.1.2 形態影響空間網絡結構

將研究靶區的空間形態與對應的網絡結構對比分析可知，公園空間形態對空間節點關系的構建有著極大影響，進而影響網絡的結構。有些公園由于河流、地形等現狀條件因素，其網絡結構分散，如鴻恩寺公園由于地形阻隔使其空間節點關系可達性與交互性減弱，網絡結構呈松散的環狀分布(圖7-1)；在緊湊型公園中，居民通過交流、運動和娛樂等活動更容易增強空間節點間的聯系，呈現環狀或組團狀的集中式社會網絡結構形態，如碧津公園布局較為緊湊，其網絡集中性與緊密度較好(圖7-2)；在形態較為不規則與松散的公園中，居民之間通過觀賞游覽、運動健身、休閑娛樂等活動產生聯系的可能性降低，減弱了公共空間的交互性與互動性，使空間網絡結構呈現帶狀或樹枝狀形態，如石門公園空間節點分布較為松散，其網絡集中性較差(圖7-3)。

3.1.3 功能影響空間網絡結構

將研究靶區的功能與對應的空間網絡結構對比分析可知，公園的功能定位在一定程度上影響著空間節點關系，從而影響網絡結構。具體而言，3個研究樣本功能存在差異，主要包括文化娛樂、休閑、觀賞游覽、運動健身和兒童活動等類型，其網絡結構完備度、穩定性、層級性各異。在以休閑、觀賞游覽、運動健身為主的公園中，公共空間節點關系較松散，空間結構雖有一定層級性，但稍微缺乏活力，如鴻恩寺公園；在功能較為豐富如以文化娛樂、兒童活動、運動健身和觀賞游覽等為主的公園中，各空間節點的互動性較強，公園空間結構較為穩定，較有活力，如碧津公園與石門公園。

3.2 公共空間結構布局優化

主要從2個層面展開：1)空間網絡結構自身調整，通過提高網絡結構的完備性、穩定性和層級性等方式，優化與完善構建的整體網絡特性和實施策略；2)基于網絡的空間規劃，以空間網絡的完備性、穩定性和層級性中的平均距離、Lambda集合、k-核、中心勢等指標為依據，將其含義對應于公園空間的優化，指導公園的空間格局保護、公共服務設施與基礎設施規劃，以及分期實施等。

以空間布局優化為例，依據網絡結構“k-核”成分的計算與分析，可指導公園各片區空間的確定。具體指將公園中“k-核”成分包含的空間節點所在區域確定為一級空間片區范圍，公園范圍內的“(k—n)核”(n≥1)成分包含的空間節點所在區域確定為二級空間片區范圍，以此類推，形成各級空間片區。以鴻恩寺公園的空間等級劃分為例，將5-核所在區域范圍劃定為一級空間片區。

4 結語

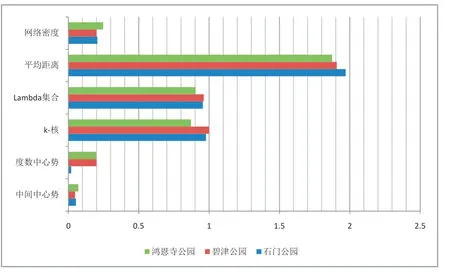
圖5 研究對象網絡結構對比分析

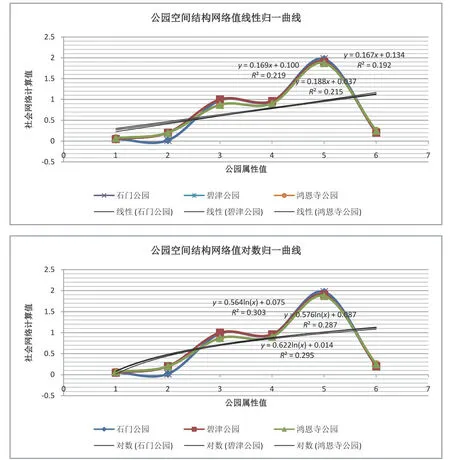
圖6 公園空間結構網絡值歸一化處理

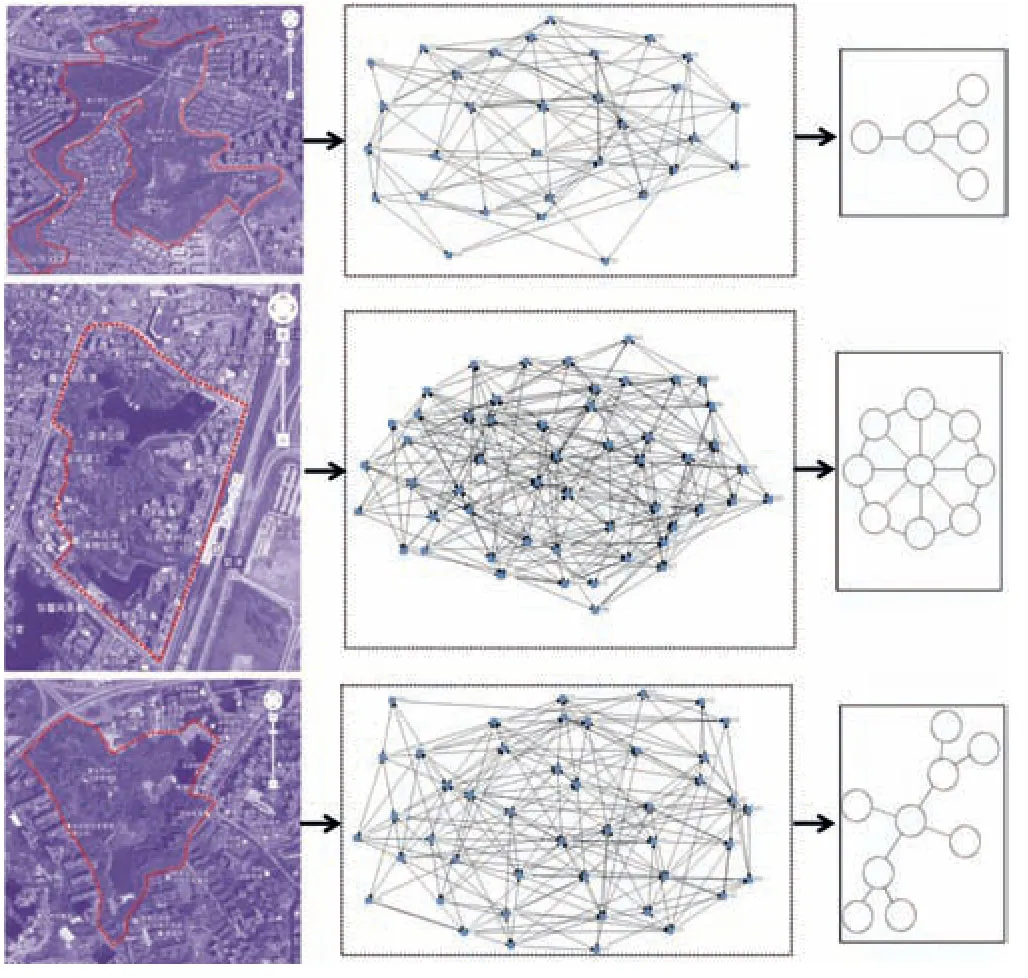
圖7 地形、形態與空間網絡結構的相關性(7-1 鴻恩寺公園；7-2 碧津公園； 7-3 石門公園)

本研究嘗試把網絡理論引入空間規劃設計研究的交叉領域，借鑒社會網絡分析的理論體系和技術方法，應用于公園空間結構網絡模型構建分析與布局優化。相較于常規的調查研究方法或定性判斷，本研究具有以下幾點創新之處：1)客觀選取研究對象與構建指標，針對公園空間混雜、破碎化和衰敗等現象，選取空間中活動者的關系構建空間網絡模型，將居民與空間的關系通過可視化的方式表現；2)基于可視化的拓撲結構，將傳統上旨在進行定性分析的內容，通過網絡模型進行定量化測試與計算；3)針對網絡自身的控制策略，契合公園空間本身與網絡的完備性、穩定性和層級性三方面特性，提出了公園空間規劃設計與布局優化基本策略，包括空間格局保護、基礎設施和公共服務設施規劃等，希望為公園空間結構優化提供科學參考。

期望相關研究從以下三方面進行拓展：1)公園空間關系的完整性，本研究由于客觀因素，對于網絡模型“線”的選取僅局限于“交互關系”，但空間節點之間的關系還包括可達性、包含性等，因此在接下來的研究中，進一步豐富空間關系的外延，完善公園空間中關系的語義模型，使其構建出的網絡模型更接近公園空間之間客觀真實存在的關系結構；2)公園樣本量的拓展性，出于研究時間與周期的考慮，本次研究靶區僅選擇了重慶地區的3個山地公園，這會在一定程度上影響理論判斷與影響機制的廣泛性與客觀性，故而希望在今后的研究中能擴大公園樣本量，從而加強結論的準確性；3)公園空間網絡的動態性，本研究重在對不同公園空間網絡結構的橫向比較，但公園中的空間關系處在不斷變化中，因此未來宜對公園在不同時間段的空間關系變化進行對比分析研究，從而有針對性地動態指導公園的空間結構規劃與布局。

注：文中圖片均由作者繪制。