基于性傳播疾病的對逼近模型及分析

趙小倩， 秦 鵬， 張菊平

(1.中北大學理學院， 太原 030051； 2.中北大學電氣與控制工程學院， 太原 030051；3.山西大學復雜系統研究所， 太原 030051)

性病，全名為性傳播疾病，是以性接觸為主要傳播方式的疾病.國際上將20多種通過性行為或類似性行為引起的感染性疾病列入性病范疇.較常見的性病有淋病、梅毒、非淋菌性尿道炎和艾滋病等.其中，梅毒、淋病和艾滋病等8種性病被列為我國重點防治的性病[1].因此，了解性傳染病的傳播機理從而制定相應的防控措施非常重要.王燕等[1]研究了一類具有季節性和疫苗接種的SIR傳染病模型對控制傳染病的影響，揭示了傳染病的傳播速度小于初始患者為隨機分布時的速度；秦文惠等[2]研究了具有一般接觸率和用于治療的SIS對逼近模型及其動力學性質，針對2種菌株是否可以獨立生存，建立了一個在規則網絡上2種菌株有交叉感染的SIS對逼近傳染病模型；李梁晨等[3]的研究，了解病毒在人體內的感染、受制、清除等動力學過程；Carnett[4]針對梅毒提出梅毒螺旋體在易感性伴侶和感染性伴侶接觸過程中具有較高的傳播可能性.而性伴侶之間的接觸形成了一個接觸網絡，因此，以接觸網絡為基礎構建網絡模型來研究性傳播疾病會更加切合實際，建立的傳染病模型也會更加精確[5-9].對逼近(Pair-Approximation)模型主要研究網絡中不同狀態的節點及其之間的連邊(對或二元組)隨時間的變化規律， 是網絡傳染病模型的一種[10-15].Moris等[16]提出了網絡中性伴侶對傳染病傳播的影響；Ghani[17]探討了不同網絡方法在性病流行病學中的作用；Bauch[18]探索了網絡中對逼近在研究性病過程中的應用；Kim[19]討論了在性傳播過程中傳播率在男性對女性和女性對男性之間可能不同；Miller等[20]給出了傳染病在網絡傳播中已有的方法和當前面臨的挑戰[21].本文主要基于接觸網絡建立異性戀中性病傳播的SIS對模型，并對其進行分析.

1 模型的建立

假設網絡中的總人口數為N，分別用m和f表示異性戀接觸網絡中的男性和女性，女性總人口為Nf(t)，男性總人口為Nm(t)，從而有N(t)=Nf(t)+Nm(t).將人群分為易感者(S)和染病者(I)，分別用Sf(或Sm)和If(或Im)表示女性(或男性)易感者和染病者，[Sf(t)](或[Sm(t)])和[If(t)](或[Im(t)])表示t時刻女性(或男性)易感者和染病者的數量.[AB]表示A-B連邊的數量，[ABC]表示A-B-C三元組的數量，其中A，B，C∈{Sf，Sm，If，Im}.接觸網絡上異性戀的性病傳播流程圖如圖1所示.

圖1 接觸網絡上異性戀的性病傳播流程圖Fig.1 Flow chart of STD transmission on the heterosexual network

根據圖1建立網絡上異性戀的性傳播SIS對逼近動力學模型為:

(1)

其中，λ1(λ2)表示易感者女性(男性)與染病者男性(女性)接觸的傳染率，γ1(γ2)表示女性(男性)染病者的恢復率.

因為

所以N(Nf，Nm)為常數.假設節點的染病者鄰居服從二項分布，有逼近公式[10]：

(2)

其中A，B，C∈{Sf，Sm，If，Im}.

由異性網的平衡條件有

nmNm=nfNf，

[SfSm]+[SfIm]+[SmIf]+[ImIf]=nfNf.

(3)

將(2)、(3)代入模型(1)，得到如下系統:

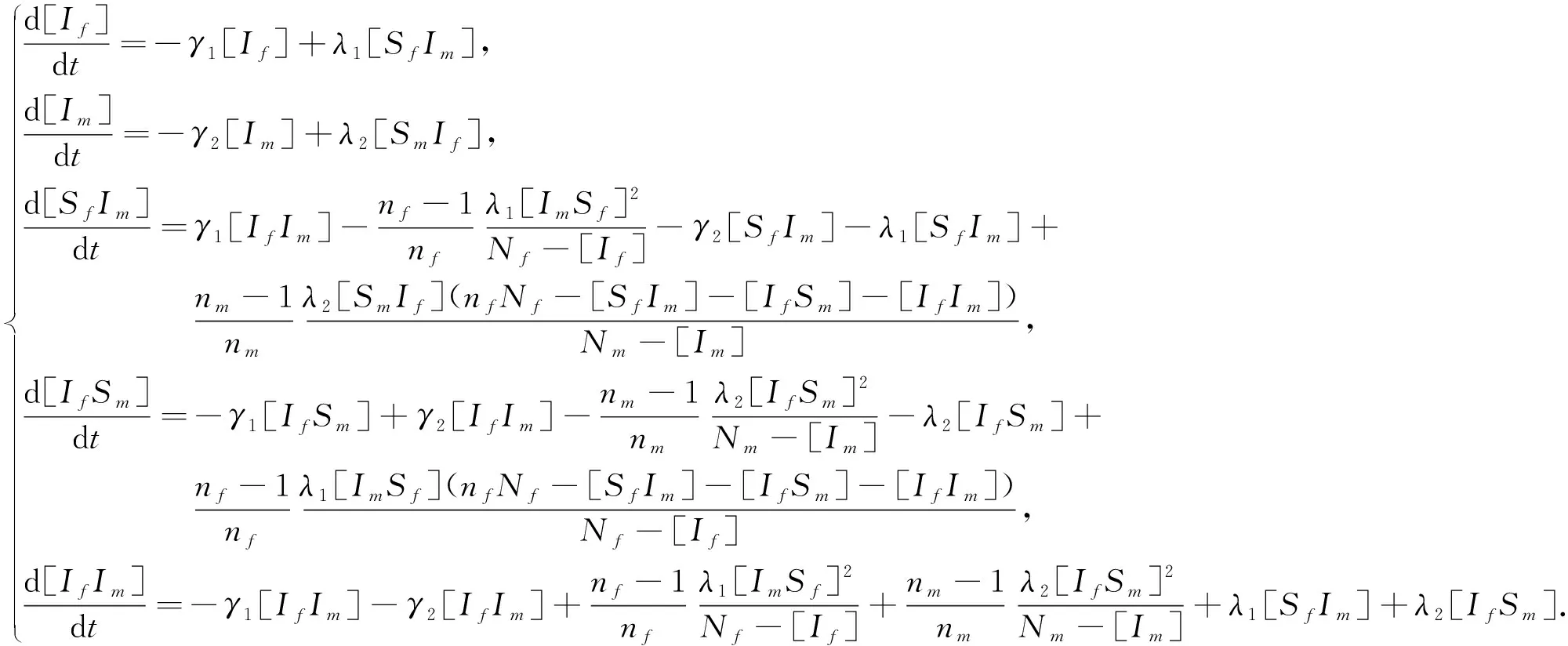
(4)

容易證得系統(4)正向不變集為

0≤[Im]+[If]≤N，

0≤[SfIm]+[IfSm]+[IfIm]≤nfNf}.

2 無病平衡點和基本再生數

系統(4)有無病平衡點E0=(0，0，0，0，0)，它在E0處的雅可比矩陣JE0為

(5)

計算得(5)的特征方程為

(τ+γ1)(τ+γ2)(τ3+τ2a1+τa2+a3)=0，

其中，

a1=2γ1+2γ2+λ1+λ2，

λ1λ2nf+λ1λ2nm-λ1λ2nfnm，

λ1λ2nmγ1-λ1λ2nfnm(γ1+γ2).

特征方程有兩個特征根為-γ1和-γ2，其余特征根滿足

τ3+τ2a1+τa2+a3=0.

(6)

由Hurwitz判據知，當H1>0，H2>0，H3>0時，雅可比矩陣的所有特征根均具有負實部，則系統(4)的零解局部漸近穩定，其中，

H1=a1>0，

H2=3(λ1+λ2)(γ1+γ2)2+

(γ1+γ2)((7γ1γ2+(λ1λ2)2))+

γ1λ1λ2(nm+2nf)+λ1λ2(nf+nm)(λ1+λ2)-

λ1λ2nfnm(λ1+λ2+γ1+γ2)，

H3=(γ1γ2(λ1+λ2+γ1+γ2)+

λ1λ2(γ2nf+γ1nm)-(γ1+γ2)λ1λ2nfnm)H2.

要使H2>0，H3>0，只需H2>0，a3>0，即

其中，

因為M>H，故只需滿足

定理1當R0<1時，系統(4)的零解是局部漸近穩定的，當R0>1時不穩定.

3 正平衡點的存在性

下面討論系統(4)正平衡點的存在情況.

令系統(4)后4個方程的右端為零，可得

(7)

將(7)代入系統(4)第5個方程的右端令其為零，可得關于[If]的一元二次方程:

P[If]2+Q[If]+W=0.

(8)

其中，

a=γ1+nfλ1，b=γ2+nmλ2，

(R0-1)(nfλ1b+nmλ2a)nfNf，

方程(8)判別式為

Δ=(R0-1)2(A-B)2+

2(R0-1)(A-B)(C-D)+(C+D)2.

(9)

其中，

A=nfλ1b，B=nmλ2a，

將方程(9)看成Δ關于R0-1的一元二次函數，求函數的最低點為

4DC>0.

下面分情況討論一元二次方程(8)根的存在性.

1)當R0>1時，有W>0.

(1) 當P<0且Q>0時，若滿足

(2) 當P<0且Q≤0時，若滿足

(3) 當P>0且Q<0時，若滿足

方程(8)有兩個正根，則系統(4)有兩個正平衡點，

和

其中，

3)當R0<1時，有W<0.

當P<0，Q>0時，方程(8)有兩個正根，則系統(4)有兩個正平衡點，

和

其中，

因此，總結如下表1所示.

表1 正平衡點的存在性

4 數值模擬

下面通過數值模擬驗證理論分析的正確性.取

Nf=80，Nm=60，nf=3，nm=4，

γ1=0.44，γ2=0.1，λ1=0.08，λ2=0.09，

則有R0>1，P<0，Q>0，系統(4)存在唯一的正平衡點且是穩定的(見圖2).

圖2 R0>1，P<0，Q>0時的時間序列圖Fig.2 Time series diagram，when R0>1，P<0，Q>0

取

Nf=80，Nm=60，nf=3，nm=4，

γ1=0.42，γ2=0.1，λ1=0.08，λ2=0.09，

則有R0>1，P<0，Q<0，系統(4)存在唯一的正平衡點且是穩定的(見圖3).

取

Nf=80，Nm=60，nf=3，nm=4，

γ1=0.1，γ2=0.15，λ1=0.06，λ2=0.07，

則有R0>1，P>0，Q<0(用實線表示).在參數不變，當Nf=40，Nm=30時(用虛線表示) (見圖4).

進一步給出了R0關于參數γ1對[If]的影響(見圖5).

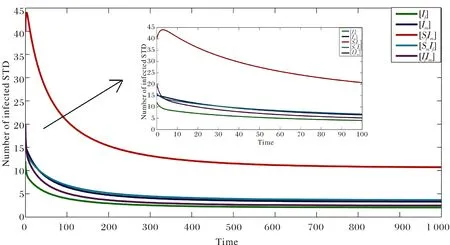
圖3 R0>1，P<0，Q<0時的時間序列圖Fig.3 Time series diagram， when R0>1，P<0，Q<0

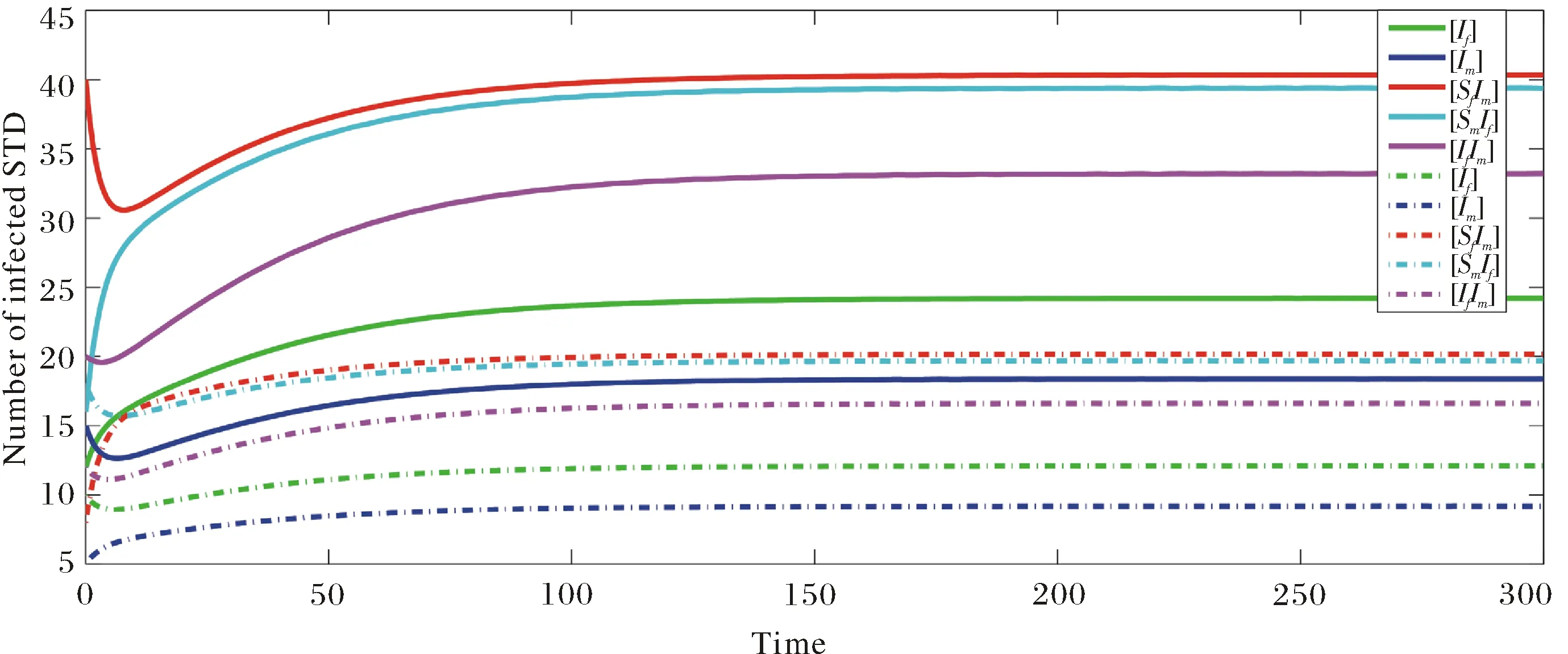
圖4 R0>1， P>0，Q<0時的時間序列圖Fig.4 Time series diagram，when R0>1， P>0，Q<0

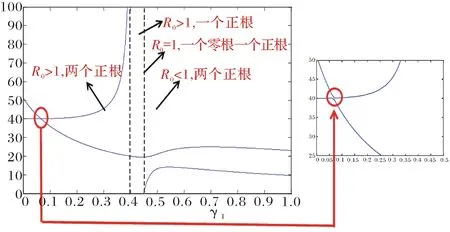
圖5 γ1對[If]的影響Fig.5 γ1impact on[If]

5 結論

本文用網絡對逼近傳染病模型來研究異性戀之間的傳染病，建立了靜態網絡上性傳播疾病的SIS對逼近傳染病模型.通過理論分析證明了無病平衡點的存在性及其局部穩定性，得到了基本再生數R0.當R0<1時無病平衡點局部漸近穩定，當R0>1時無病平衡點不穩定.分情形討論了正平衡點的存在性，并通過數值模擬驗證了理論結果的正確性.