分數階Birkhoff系統的積分因子與守恒量

楊麗霞， 張 毅

(1.蘇州科技大學數理學院， 江蘇 蘇州 215009； 2.蘇州科技大學土木工程學院， 江蘇 蘇州 215011)

在研究相關的動力學問題時，分數階微積分產生了重要作用.在實際應用中，分數模型較整數階模型而言，更加符合實際意義，結論更加精確.1996年，Riewe首次建立了非保守力學系統的分數階模型[16-17].隨后，Frederico和Torres建立了分數階Lagrange系統和分數階Hamilton系統的Noether定理[18-19].近年來，分數階模型下約束力學系統的守恒量研究已經取得重要進展[20-25].張毅等[26]提出并證明了Riemann-Liouville導數下分數階Birkhoff系統的Noether定理，束方平等[27]將積分因子法應用于分數階Lagrange系統.本文將用積分因子法研究基于Riemann-Liouville導數的分數階Birkhoff系統的守恒量，從而建立該系統的積分因子定義與守恒定理.

1 Riemann-Liouville分數階導數及其基本性質

假設在區間[a，b]上，函數f(t)連續且可積，則Riemann-Liouville分數階左導數定義為

(1)

右導數定義為

(2)

其中，Γ(*)是Gamma函數，α是導數的階，且0≤α<1.

(3)

(4)

(5)

(6)

(7)

2 分數階Birkhoff系統及其積分因子

由2n個Birkhoff變量aμ=aμ(t)來描述的分數階Birkhoff系統，該系統的Birkhoff函數為B=B(t，aν)，Birkhoff函數組為Rμ=Rμ(t，aν)，在Riemann-Liouville導數下分數階Birkhoff方程可表示為[26]

(μ，ν=1，2…，2n).

(8)

如果α→1，則方程(8)成為

(μ=1，2，…，2n)，

(9)

方程(9)是經典Birkhoff方程[2].

定義1如果存在函數集ξμ(t，aμ)，使得不變式

恒等地化為

(10)

其中，函數G，ξ0和λμ與t，aμ相關，則稱函數集ξμ(t，aμ)是分數階Birkhoff方程(8)的積分因子.

3 分數階Birkhoff系統的守恒定理

假設函數集ξμ(t，aμ)是方程(8)的積分因子，將式(8)代入式(10)，得到

(11)

故有

命題1若函數集ξμ(t，aμ)是分數階Birkhoff方程(8)的積分因子，那么沿著系統的運動微分方程，存在守恒量I(t，aμ)，形如

(12)

如果分數階Birkhoff系統(8)存在積分因子ξμ，則守恒量I中的函數集G，ξ0，ξk一定滿足必要條件(10).由式(8)，可將(10)化簡成

(13)

展開上式，并將式(8)代入，得到

(14)

如果必要條件(14)的解G，ξ0和ξμ使得表達式(12)等號右邊成為一個常數，即

若C0為定值常數，則可稱此組解G，ξ0，ξμ為奇異函數組；反之，若C0為任意常數，則可稱此組解為非奇異函數組.故有如下命題.

命題2對于分數階Birkhoff系統(8)，若有非奇異函數組G，ξ0，ξk和λμ為必要條件(14)的解，則該分數階Birkhoff系統存在一個形如式(12)的守恒量.

命題1和命題2統稱為積分因子理論.

4 廣義Killing方程

用上述積分因子理論尋找該系統(8)的守恒定理的過程中，重點是需要找到非奇異函數組G，ξ0，ξk和λμ，滿足其必要條件等式(14).

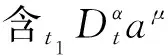
(15)

(μ=1，2，…，2n).

(16)

方程(15)和(16)是關于(4n+2)個未知函數G，ξ0，ξμ和λμ的(2n+1)個偏微分方程.因此，尋找必要條件(14)的非奇異函數組解便轉化為尋找式(15)和(16)的非奇異函數組解.從式(15)和(16)的方程中可以看出，其未知函數的個數明顯多于其廣義Killing方程式的個數，因此該方程組的解不唯一.在尋找其廣義Killing方程的解過程中，可先適當選取部分G，ξ0，ξμ，λμ的值，便可得到方程(15)和(16)的解，故可求得此系統的守恒量.

命題3對于所論分數階Birkhoff系統(8)，若廣義Killing方程(15)和(16)存在非奇異函數組解G，ξ0，ξμ，λμ，則該系統(8)存在一個形如式(12)的守恒量.

此外，為了得到非奇異函數組解G，ξ0，ξμ和λμ，也可將該系統方程(8)直接代入必要條件(14)，得到

(17)

可以通過直接解方程(17)，得到非奇異函數組解G，ξ0和ξμ，從而得到此系統(8)的形如式(12)守恒量.

5 特例——分數階Hamilton系統的積分因子

由Lagrange系統、Hamilton力學系統的從特殊到一般的發展，有了Birkhoff力學系統.

若取

B=H，

(18)

其中，qk和pk分別為廣義坐標和廣義動量，H=H(t，qk，pk)為Hamilton函數，則可將分數階Birkhoff系統(8)退化為如下分數階Hamilton方程

(19)

由定義1，得到下面定義2．

(20)

其中，函數G，ξ0，λk與t，qk，pk相關，則稱函數集ξk=ξk(t，qk，pk)是該系統方程(19)的積分因子.

由命題1和命題2便可得下面命題4．

命題4若函數集ξk(t，qk，pk)是該系統方程(19)的積分因子，則由該分數階Hamilton系統的運動微分方程存在守恒量I，形如

(21)

命題5對于分數階Hamilton系統(19)，若有非奇異函數組G，ξ0，ξk和λk為必要條件

(22)

的解，則此系統存在一個形如式(21)守恒量.

(23)

(24)

命題6對于分數階Hamilton系統(19)，若有非奇異函數組G，ξ0，ξk和λk為廣義Killing方程(23)與(24)的解，則此系統存在一個形如式(21)守恒量.

6 算例

若分數階Birkhoff系統的Birkhoff函數B和Birkhoff函數組Rμ分別為

(25)

R1=a2，R2=0，R3=a4，R4=0.

(26)

分數階Birkhoff方程(8)給出

(27)

將式(27)代入廣義Killing方程(15)和(16)，得到

(28)

(29)

(30)

方程(28)～(30)有解：

(31)

(32)

(33)

(34)

由命題3可得

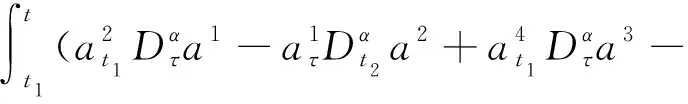
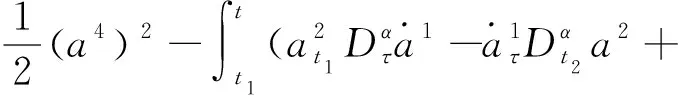
方程的解(31)～(34)是非奇異函數組解，故I1、I2、I3、I4是系統的守恒量.

7 結論

尋找約束力學系統的守恒量是分析力學研究的重要內容，積分因子法因其計算簡單，適用范圍廣而得到廣泛應用.文章的主要工作：一是定義了分數階Birkhoff方程(8)的積分因子；二是建立了由積分因子理論得到的分數階Birkhoff系統的守恒定理，由其積分因子理論得到了該系統的守恒量形式；三是建立了分數階Birkhoff系統的廣義Killing方程，給出了求解守恒量的具體方法；最后給出分數階Hamilton系統的積分因子定義，并給出其守恒定理.文章的方法和結果可進一步推廣及應用于基于不同分數階導數的分數階約束力學系統.