基于旅游生產線的景區景點閑置、過載和不確定條件下容量決策分析

熊 浩， 鄢慧麗

(1.海南大學管理學院， 海口 570228； 2.海南大學旅游學院， 海口 570228)

對于包含有多個景點的景區或主題公園，學者劉益較早指出了以景點周轉率為出發點的景區容量計算模型具有明顯的局限性，認為景區周轉率計算相比景點周轉率更加合理[1].后來，學者黃羊山發表多篇論文對傳統的景區容量算法進行了較為深入的分析，進一步指出了傳統景區容量計算模型的錯誤}，并提出了基于流函數的計算模型[3]和“求小法”計算方法[4].假設游客動態勻速的移動，考慮了游覽順序、線路時間、游覽時間等因素，比較合理的分析了游客在景區的容量計算問題.

近來，學者鄢慧麗和熊浩在黃羊山文章的基礎上結合生產運作管理的相關理論提出了旅游生產線的概念[5]，更加合理的解釋了景區容量計算的生產運作特征，并且推導出了基于旅游生產線的景區容量及準入批量的計算方法[6-7].旅游生產線理論利用生產運作理論較好的解釋了為什么景區容量受周轉率小的短板景點影響，為什么景區景點周轉率不相等時不能取平均值，指出了景區內景點時間均衡與否和景點容量均衡與否，是導致景區容量計算復雜性的原因.同時也給黃羊山學者提出的流函數提供了更為合理的理論支撐.

然而，關于旅游景區景點閑置、過載和不確定條件下容量決策問題仍然需要進一步完善和更加深入的探討.本文根據旅游生產線的生產批量、生產批次和總接待量公式，進一步分析了準入批量對總接待量的影響、景區旅游生產線的閑置與過載、景點容量和游憩時間不確定對容量控制決策的影響.這些問題的深入分析能更加真實準確的應對高峰期景區景點容量控制問題，從而幫助景區科學合理的進行景區景點容量設計和容量控制.

1 景區旅游生產線

1.1 景區旅游生產線的基本原理

假設一個景區包含若干個景點，將這些景點看作不同的生產工序，則景區內所有的景點構成了一條為游客提供旅游服務的生產線.在景區旅游生產線中，游客是“工件”；景點是“工序”；游客在景點的游憩時間是“加工時間”.每道工序可以進行批量加工，且景點容量就是工序的單批加工能力；旅游生產線的瓶頸工序為周轉率最小的景點，稱為瓶頸景點.

對于旅游景區的旅游生產線，本文引入了旅游子景點的概念對游覽時間較長的景點進行分解，使景區中所有子景點的游覽時間相同，從而使得旅游生產線具有相同的生產節拍.另外，為了分析的方便，本文將使用和文獻[7]中相同的范例.

范例：某景區擁有2個景點，景點1的設計游覽時間和容量分別為1 h和100人，景點2的設計游覽時間和容量分別為1.5 h和120人，假設工作日時長為8 h.

1.2 基于景區旅游生產線的容量優化模型

假設給定某個景區有m個景點，每個景點的設計容量和設計游覽時間分別為：Ci和ti，則景區各個景點的周轉率為Zi=Ci/ti.如果t0為景點游覽時間{t1，t2，…，tm}的最大公約數，則景點i分解后的子景點數量為ni(ni=ti/t0)，總子景點數為：

(1)

分解后各個子景點的設計游覽時間都變為t0，設計容量變為：

qi=Ci/ni=t0Ci/ti.

(2)

然后，依據景區生產線順序移動的生產周期公式，分別推導出有游覽順序和無游覽順序的景區容量控制最優決策(詳見文獻7).

1)有游覽順序

根據景區是否具有游覽順序，分別基于景點分解的景區旅游生產線實際上可以看作為以子景點為工序，以游客為工件的生產線.根據平行移動的生產線批量決策模型可以推導該生產線的批量、批次數和工作時間的接待量分別為：

Q0=qmin=t0Zmin，

(3)

(4)

Cmax=[T/t0-(N-1)]qmin=

[T-(N-1)t0]Zmin=

(5)

其中，qmin=min {qi，i=1，2，…，m}為瓶頸子景點對應的生產能力，Zmin=min{Zi，i=1，2，…，m}為瓶頸景點對應的生產能力，一般又稱為最小周轉率；Q0為批量即為旅游景區的準入游客批量，M為景區在工作時間內能夠完成的批次數，Cmax為旅游景區在工作時間T內的產量即為接待量.需要注意，式(5)中當t0是景區景點的公約數時最右邊才能成立，因為接待批量和接待批次都需要取整.

2)無游覽順序

無游覽順序的景區，意味著剛開始時可以允許多批旅客進入，假設游客會自動散布到各個有剩余容量的景點.后續的批量計算方法和有游覽順序的景區的批量和接待量計算方法相同.第一批進入批量為：

(6)

2 景區旅游生產線的閑置和過載分析

2.1 景區旅游生產線的閑置情況分析

對于有游覽順序的景區，從景區開放游客進入初期，直到準入M批次的游客之后，景區的各個景點才會都有游客進入；到景區當天停止營業的末期最后第M批游客依次離開景區時，景區線路中所有子景點依次開始閑置.可以看出，由于必須保證游客在營業時間內完成所有景點的游憩，并且不允許任何景點存在過載，則在期初和期末景點必然會出現一段時間的閑置.這種閑置是由于系統設置的原因造成的，不可避免，稱為系統閑置.

另外，無論是否有游覽順序，都有可能存在一種由于景點周轉率設置不均衡造成的閑置.這種閑置是由于景點周轉率不均衡造成的，可以通過調整設計來解決，稱為不均衡閑置.

以上所謂的閑置是相對景點的設計游覽時間和游覽容量而言的.在充分利用的情況下，景區中的每個景點的最大接待量應該等于其周轉率乘以營業時長.因此，基于旅游生產線的系統閑置和不均衡閑置表達式分別為：

W0=(N-1)qmin=

(7)

Wi=T(Zi-Zmin).

(8)

式(7)是系統閑置，等于期初和期末的平均閑置時間乘以最小周轉率；式(8)是周轉率較大的景點的不均衡閑置，景點周轉率與最小周轉率的差值乘以景區營業時長.

對于景點游覽時間的不均衡，由式(7)可知，景點游覽時間的不均衡通過影響最大公約數t0而影響閑置率.在景區總游覽時間和瓶頸周轉率不可變的情況下，t0越大系統閑置越小.當景點游憩時間相同時，t0最大.而對于景點周轉率不均衡，景點周轉率差異直接影響了景點閑置.由式(8)可知，景區可以在周轉率較小的區域設置休息區等策略，使景區中景點周轉率差異盡量減少.

范例分析：時間間隔為0.5，景點1分解為2個景點，景點2分解為3個子景點，子景點周轉率分別為：50人/h和40人/h.接待批量為480.但是，依據式(7)系統閑置為：(5-1)×40=(2.5-0.5)×80=160；依據式(8)可知，景點1的不均衡閑置為：8×(100-80)=160，景點2不存在不均衡閑置.此時為最優接待批量，如果想進一步提升接待批量就必須打破不均衡.

2.2 準入間隔非最大公約數時的閑置分析

對于高峰期多景點景區容量控制問題，需要考慮游客的感受，太長的等待進入時間間隔可能會讓游客感覺無法接受.如果人為縮短準入時間間隔，準入批量應該如何調整？調整后對整體接待數量產生什么樣的影響？

1)準入時間不是最大公約數

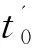
由接待量計算公式(5)可知，較小的公約數雖然會使接待批次增加，但是會使準入批量減少，從而使總接待量減少.因此，增加了景區內景點的閑置.

范例分析：景區各個景點游覽時間最大公約數為0.5，現在若取0.25、0.125和0.062 5作為公約數，準入批量分別變為：20、10、5；接待量分別減少為：460、450和445.則減少率分別為：4.17%、6.25%、7.29%.實際上，公約數繼續縮小到接近零時接待量的減少量為40，減少率為8.33%.

2)準入時間不是公約數

假設隨意選擇非公約數準入間隔時間長度t0，由于游客數必須為整數，批次數必須為整數(假設游客必須游完所有的景點)，所以利用旅游生產線進行容量控制決策時需要進行取整分析.具體的取整情況為：景點i分解后的子景點數量需要向上取整(取較大的整數)，否則游客無法完成整個景點的游玩；景區營業時間內的批次向下取整(取較小的整數)，否則最后進入的批次游客不能夠完成景區所有景點的游玩.取整雖然能夠保證游客完成所有景點的游玩，但是會增加景區中的景點閑置.

范例分析：景區各個景點游覽時間隨意選取較小的準入間隔時間為0.3，則此時景點1的分解數量為4，景點2的分解數量為5.準入批量為24，批次向下取整為18，則根據旅游生產線計算其接待批量為：432.與最優接待批量480相差48.

范例分析：景區各個景點游覽時間隨意選取較大的準入間隔時間為0.6，則此時景點1的分解數量為2，景點2的分解數量為3.準入批量為40，批次向下取整為9，則根據旅游生產線計算其接待批量為：360.與最優接待批量480相差120.

2.3 景區景點的過載分析

為了與閑置分析相對應，分析景區過載的情況，本文引入過載量的概念.所謂過載量是指景點在同一時刻接待的人數超出了設計容量.

根據文獻[7]中旅游生產線的分析，過載的分析相對比較簡單.只要景區的準入批量大于了子景點的容量上限，相應的子景點都會過載.從而，子景點對應的景點也會過載.

3 不確定條件下的旅游生產線優化分析

據上分析，對于確定條件的旅游生產線優化，只需要確定最大的公約數就能使接待批量最大.然而，對于不確定的情況，需要同時對最大公約數和準入批量進行分析.

3.1 景區中景點容量具有不確定性

當景區中景點容量具有柔性和不確定性時，如果景區景點游憩時間確定，則最大公約數不受影響.只需要分析準入批量，即分析最小的景點容量.

1) 景區中景點容量為區間數

若景區中景點容量為區間數，則可以通過概率分布函數來確定景點容量區間的下界值，從而計算出子景點容量的最小值，然后利用旅游生產線模型進行優化.

范例分析：在原范例中，若景點1的景點容量為120～150，景點2的容量為140～160，其他條件不變.準入時間間隔仍為0.5，接待批次仍為12次.此時，按照景點容量的下限值120和140進行優化，則兩個景點的子景點的最小值為.因此，計算得到的準入批量變仍為40，接待量仍為12×40=480.可見，雖然單個景點的容量都增加了，但接待量仍然保持不變.

2) 景區中景點容量為隨機數

若景區中景點容量為隨機數，且分布已知(比如均勻分布、泊松分布或正態分布等)，則可以通過景點容量區間的下界值來尋找各個子景點容量的最小值，然后利用旅游生產線模型進行優化.

范例分析：在原范例中，若景點1和景點2的容量分別為：均值分別為100和120，方差均為10的正態分布，其他條件不變.則兩個景點容量在99.87%的條件下分別為：100+3×10和120+3×10.此時利用景點容量130和150進行計算.則最小準入批量為50，接待量為12×50=600.

3.2 景區中景點游憩時間具有不確定性

當景區中景點游憩時間具有柔性和不確定性時，如果景區景點容量確定，則只需要分析最大公約數的情況.

1)景點的游憩時間為區間數

若景點的游憩時間為區間數，則可以尋找各個景點的游憩時間區間數范圍內的最大公約數，進行景點的分解，然后利用旅游生產線模型進行優化.

范例分析：在原范例中，若景點1和景點2的游憩時間分別為0.8～1.2 h和1.0～1.4 h，其他條件不變.此時，選擇0.8～1.2和1.0～1.4這兩個區間的最大公約數1.2，此時兩個景點都不需要分解.這時兩個景點的游憩時間按照1.2來計算.因此，計算得到的準入時間間隔仍為1.2，接待批次為6-(2-1)=5，接待量為5×83=415.

2)景點的游憩時間為隨機數

若景點的游憩時間為隨機數，且分布已知(比如均勻分布、泊松分布或正態分布等)，則可以依據概率來計算景點的游憩時間，然后計算最大公約數.

范例分析：在原范例中，若景點1和景點2的游憩時間分別為：均值分別為0.9和1.2，方差均為0.1的正態分布，其他條件不變.則兩個景點游憩時間在99.87%的條件下分別為：0.9+0.3和1.2+0.3.此時利用景點游憩時間1.2和1.5進行計算.最大公約數0.3，子景點周轉率分別變為：25和24人/h，準入批次為：26-(9-1)=18.因此，準入時間間隔為0.3，準入批量為24，接待量為，18×24=432.

4 結論

本文對基于旅游生產線理論的景區容量問題進行了更加深入的分析.根據旅游生產線的準入時間間隔、準入批量、準入批次和總接待量等的計算公式，進一步討論分析了批量對總產量的影響、景區旅游生產線的閑置情況、景區旅游生產線的非公約數批量對應的過載量分析以及景點游憩時間不確定情況，并得出了一些有用的結論.

1) 景區景點的閑置由兩種原因造成：系統原因和周轉率不均衡原因.系統原因是由于游客一定要完成所有的景點才會離開景區這種系統特征所造成的，無法避免；而周轉率不均衡是可以通過設計進行改善的.

2) 如果準入時間間隔不等于各個景區景點游憩時間的最大公約數，則閑置會增大，從而減少最大接待量.

3) 景區景點的過載僅受準入批量的影響，不受準入時間間隔(游憩節拍)的影響；只要準入批量大于景區景點容量就會導致過載.

4) 景區景點游憩時間和容量不確定條件下也可以利用基于旅游生產線的容量決策模型進行高峰期的容量控制決策.

綜上所述，基于旅游生產線的景區景點閑置、過載和不確定條件下的容量決策分析，能夠更加科學合理地計算不同條件下的準入批量，有利于景區更好地進行高峰期景區容量控制，提高景點容量利用率.