奇數齒數圓柱齒輪齒頂尺寸的計算探討
陳 林
(南京高速齒輪制造有限公司,江蘇 南京 211123)
齒輪是一種常見的機械傳動件,被廣泛使用在各種機械設備中。通過齒輪副的嚙合運動實現力和運動的傳遞。一個齒輪副中的兩齒輪齒數往往滿足互質的條件,以使得嚙合的機會更均等,通常相嚙合兩齒輪的齒數會存在奇數齒的情況。而齒頂圓直徑作為齒輪件加工制造過程需要控制的參數,會影響到齒輪副的重合度以及實際頂隙,通常加以公差約束,甚至會作為產品的終檢尺寸來要求。這就需要加工過程對尺寸的控制更為精準,從制造過程來看,奇數齒數由于無法直接測量齒頂圓直徑,可行的是將齒頂圓直徑換算成齒頂圓最大弦長,用量具直接檢測齒頂圓最大弦長。常用且易于操作的方法就是采用游標卡尺或者外徑卡尺來直接檢測尺寸。加工時通過控制該尺寸來間接地保證齒頂圓直徑達到設計要求,尤其是在齒形已加工好的零件再加工齒頂圓的情形就只能采用間接法保證齒頂圓尺寸的準確性。那么,尺寸轉化計算的準確性就顯得至關重要。
1 齒頂最大弦長的計算
關于齒頂圓最大弦長的計算公式,查閱文獻及生產使用情況,常用的是便于現場計算的近似公式,如下
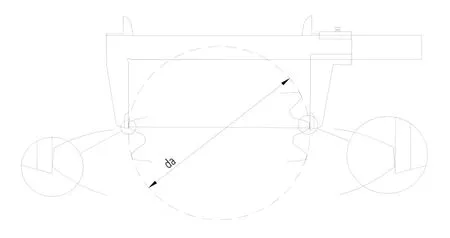
圖2 奇數齒數齒頂圓尺寸的檢測示意圖
經過仔細推敲分析并結合生產實踐,會發現上述公式計算不準確或者不符合實際檢測條件,因為測量時,卡尺的卡爪間并不能準確保證正好落在齒頂正中心位置,多次可能會得到差異較大的一系列檢測值,存在較大的測量誤差,實現齒頂圓直徑尺寸的控制。然而,最大值從理論上及實際測量時通過兩卡爪跨過相對兩齒頂的棱線,如圖2 所示。從理論上該值是唯一的,生產現場實際檢測也可以較容易地實現,測量系統性誤差較小。
由圖2 可知,齒頂圓最大弦長計算公式為

式中:ad 為齒頂圓直徑,Z 為齒數(是一個奇數)。
上述近似公式可以通過圖1 所示的幾何關系得到。
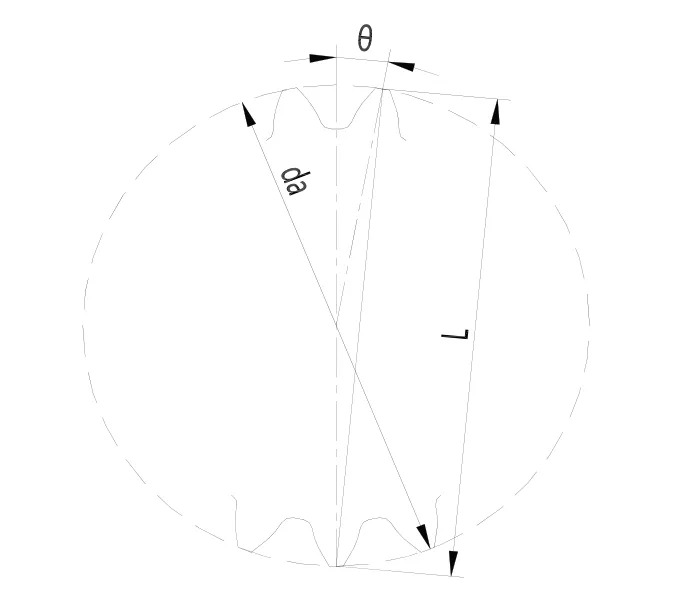
圖1 齒頂圓最大弦長近似表達
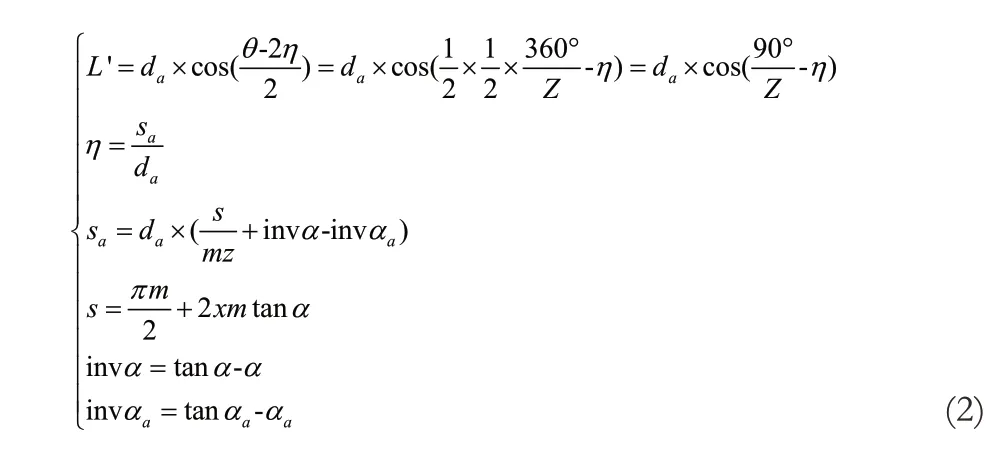
áa為齒頂圓端面壓力角。

圖3 齒頂圓最大弦長示意圖
對比上述兩種計算公式,精確計算公式需要計算齒頂圓齒厚,相比之下簡化版公式則較為簡單,方便生產現場在沒有專門的計算工具的條件下使用,下面對簡化版公式及精確計算兩種公式進行簡要的對比分析,考慮齒數對簡化版公式結果準確性的影響。以便于在誤差能夠接受的范圍內合理地選擇公式,做到“又快又準”。從直觀上看齒數越少兩者差異越大,兩者的差異體現在是否考慮了齒頂圓齒厚對應圓心角影響,如圖3 所示。
2 計算誤差分析
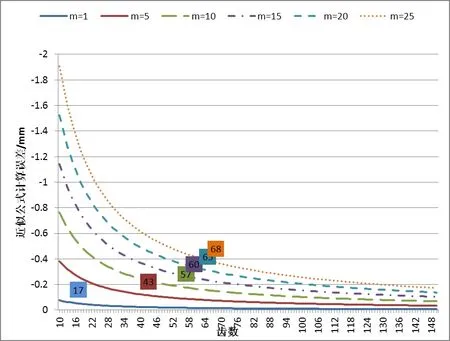
圖4 近似計算公式誤差
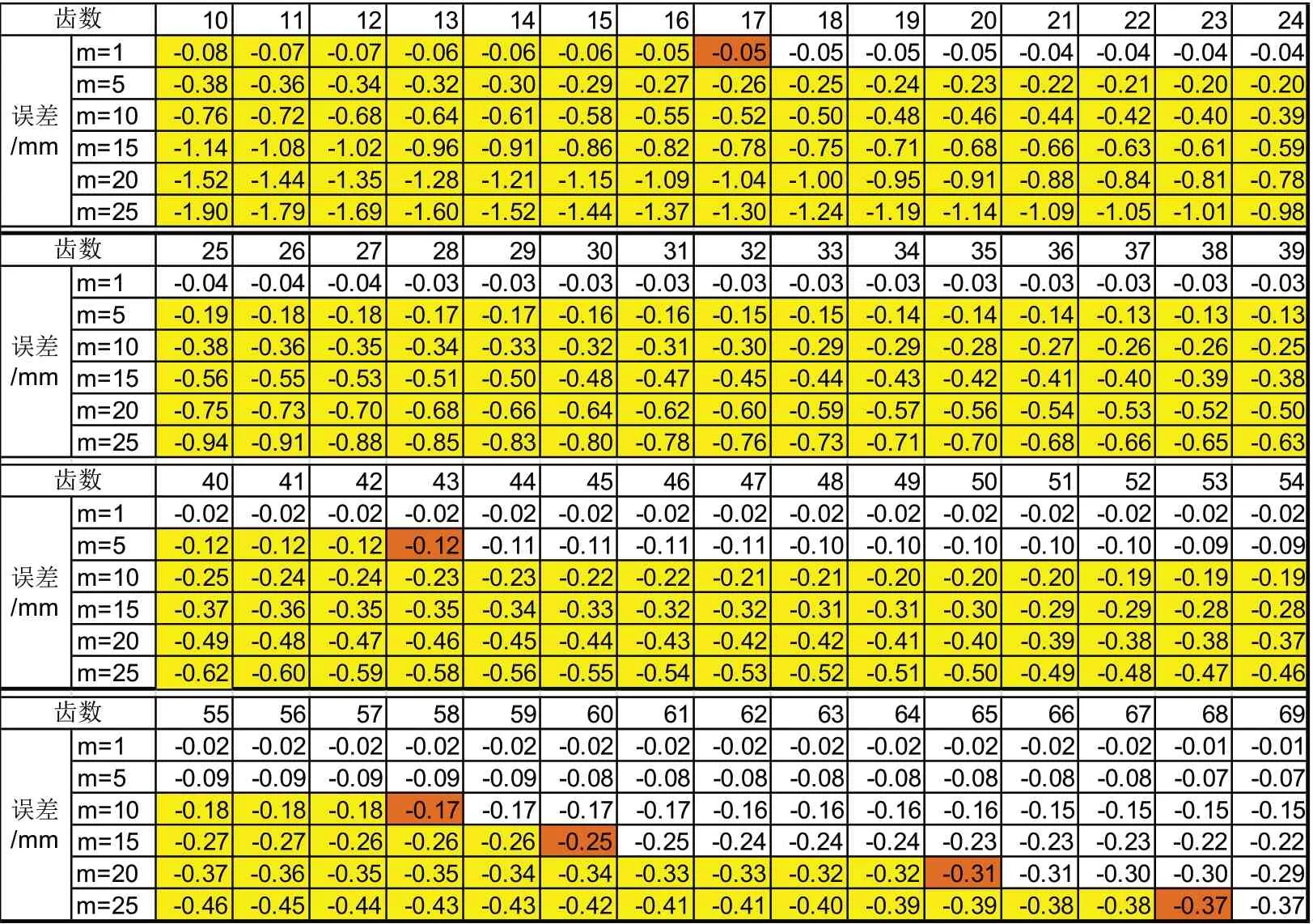
表1 近似計算公式誤差表
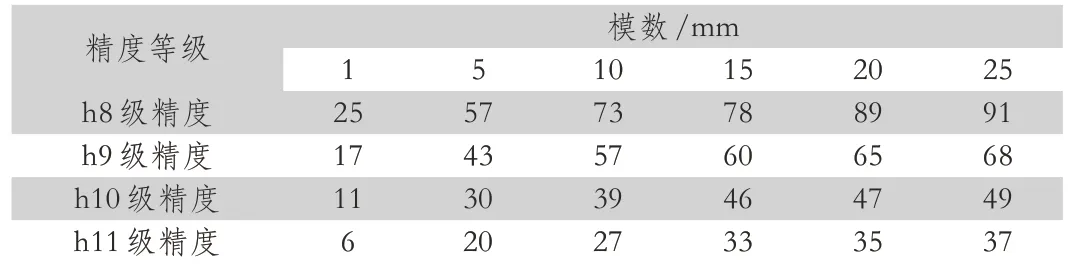
表2 各精度等級及模數對應臨界齒數
根據計算結果,可得到如表2所示不同模數各精度等級對應的臨界齒數,當齒數大于該臨界值時,相應的齒輪件采用近似公式控制的齒頂圓尺寸能夠達到相對應的精度等級。由圖4可見,隨著模數的增加,近似計算公式更易導致齒頂圓尺寸超差;如對于齒頂圓直徑尺寸要求h9級的齒輪件,理論上能保證尺寸落在公差帶內相對應模數1,5,10,15,20及25的臨界齒數分別為17,43,57,60,65和68,如圖4及表2。也就是模數為5的齒輪當其齒數不少于43時,按照近似公式結果加工的齒輪件能夠使齒頂圓達到h9級公差要求內,模數為10的齒輪件當其齒數不少于57時,按照近似公式結果加工的齒輪件能夠使齒頂圓達到h9級公差以內。
3 結論
近似公式的計算誤差與齒輪件的齒數及模數相關。相同模數條件下隨著齒數的增加誤差逐漸減小,齒數增加至臨界齒數以上時,計算誤差會減小至相應公差等級要求的誤差以內;對齒數較大的齒輪,計算誤差相對較小,能夠滿足精度要求,而對齒數較少的齒輪件則可能會使得齒頂圓尺寸超差;隨著模數的增加,臨界齒數呈現出逐漸增加的趨勢,對公式計算精確性要求更高。

