巧用圓錐曲線定義妙解高中數學競賽題

江蘇省揚州市揚州大學附屬中學 張衛兵

圓錐曲線是典型的解析幾何，是高中數學的重點和難點，主要包括橢圓、雙曲線、拋物線等內容。在初中一元二次函數的學習中，了解了拋物線最值、頂點、開口方向、單調性等知識，但是進入高中，又新增了橢圓和雙曲線知識，在原有的基礎上拓展了幾何圖形以及直線與圓錐曲線綜合問題，進一步滲透了“數形結合”思想，強調了數學模型的重要性。了解圓錐曲線定義能夠在數學競賽中快速抓住問題本質，運用數學思想和解題技巧避繁就簡式解題，邂逅數與形的魅力。

一、數學競賽中圓錐曲線知識的考查分析

本文以2000 年到2017 年全國高中數學聯賽中的“圓錐曲線”試題為研究對象，進行分析、整理、歸納和總結。“圓錐曲線”是每一年數學競賽的重點考查內容，所占分值基本在30 分左右，出題頻率高且穩定，題型選擇也多種多樣，一般包括選擇題、填空題和解答題，知識考查包括基礎知識；其與數列、不等式、平面向量、函數等知識的結合：數形結合、轉化與化歸等思想。

二、圓錐曲線學習的重要性

解析幾何是數學發展的標志性成果，圓錐曲線作為解析幾何的重要組成部分，體現了解析幾何的基本思想和能力。此外，它還是代數與幾何的橋梁，用以培養學生利用代數方法解決幾何問題的能力。圓錐曲線在高中數學教材中的所占比例較大，知識重點一直比較多。當然，解析幾何又是微積分的基礎，與高等數學密切相關，由此可見，圓錐曲線不僅是高中教學的關鍵內容，還是整個數學知識的關鍵組成部分，是培養學生數形結合思想、邏輯思維能力、數據分析能力、空間形象能力的重要途徑。

從高中教材分析來看，圓錐曲線這部分知識對文科、理科的要求不同，安排課時不同，理科生研究更為深入，難度比較大，重點考查綜合能力，會涉及向量、不等式、函數等，不僅要掌握定義、性質，還要具有很強的綜合性和轉化、化歸能力、分析能力和計算能力，自身的知識廣度與深度要達到一個新的層次；文科生研究比較基礎，只需要掌握簡單的應用，考查基礎運用能力。

三、巧用橢圓定義妙解數學競賽題

1.橢圓定義

平面內與兩定點F1、F2的距離的和等于常數2a（2a＞|F1F2|＞0）的點的軌跡叫作橢圓。兩個定點（F1、F2）叫作橢圓的兩個焦點，兩個焦點的距離叫作橢圓的焦距。其數學表達式為：|PF1|+|PF2|=2a。

一動點到定點的距離和它到一條定直線的距離的比為常數e（0＜e＜1），那么該動點的軌跡叫作橢圓，其中，定直線為準線，定點為焦點。該定義被稱為橢圓的第二定義。

2.解題范例

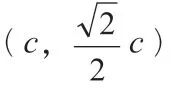
剖析：此題首先梳理出題中已知條件和橢圓性質之間的關系，然后再借助定義“橢圓上任意一點與兩定點之間的距離為2a（其中a為橢圓的半長軸長）”，最終求得橢圓離心率e。

四、巧用雙曲線定義妙解數學競賽題

1.雙曲線定義

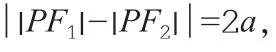
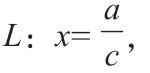
2.解題范例

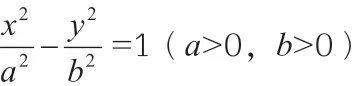
解題思路：首先根據正弦定理得到焦半徑|PF1|和|PF2|，然后再結合雙曲線定義，求得離心率。

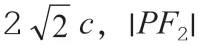
五、巧用拋物線定義妙解數學競賽題

1.拋物線定義

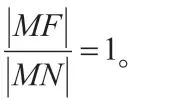
2.解題范例

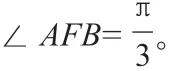
解題思路：首先巧用拋物線上的點到焦點的距離與其到準線的距離進行互化，然后將其貫穿整個解題過程，最后再根據余弦定理結合不等式，求解出最大值。

由以上敘述可知，圓錐曲線知識涉獵廣泛，在用定義求解相關問題時，一般會涉及焦點和準線，習慣從曲線上的點與焦點構成的三角形入手，再利用勾股定理或正余弦定理進行求解。整個過程運用到了數形結合思想、劃歸思想等，不僅能夠培養學生的數學學習思維，還可以提升數學學習能力，找到最優解題途徑，優化數學學習過程。因此，在教學實踐中，教師要注重對學生進行圓錐曲線模塊知識的訓練，讓其感受數與形的美，提升數學綜合素養。