骰子的組合數探究
2020-03-16 05:42:02四川省宜賓市南溪區第一中學張玄逸
數學大世界 2020年3期
關鍵詞:含義
四川省宜賓市南溪區第一中學 張玄逸
如果能夠僅僅通過交換而不改變數值得到的組合只算作一個組合,比如——
那么這一組骰子可以擲出多少不同的組合?
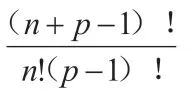
可惜的是作者并沒有給出證明過程。
骰子與組合無法直接建立特定倍數關系,因為骰子們點數的種類和數量都是變量。
本文試從公式出發倒推證明過程,最終回歸組合。
一、排序
首先必須把每個數列中的數字重排。有序數組更易發現規律。將其記為ai。
二、構造數組
構造bi,b1表示有幾個1,b2表示有幾個2,以此類推。上述組合可以改寫為:0 2 1 0 2 1,
另外有很明顯的幾點:a1≥1 ;a6≤6 ;ai-1≤ai。
看似平常的三點可以啟發我們構造另一個數組:
令ci=ai-ai-1,即ci為ai的差分數組。
經驗證,兩個數組均可以推導得到公式,因此下文就以更難一點的差分數組來證明。
三、規定
差分數組的含義為當前數字比前一個多了多少,那么c0該等于幾?根據后面的ci范圍為[0,5],類比得到c0=1,c1∈[0,5],否則下一步操作無法等價進行。
四、隔板法
現在已經類似于隔板法了,因為最后一個數最多比c0多5,所以有5 個小球。因為最后一個數不一定為6,因此隔板仍需6 塊,而相鄰兩隔板間的距離即為ci。但會導致此種情況。以上文2 2 3 5 5 6 為例。
隔板法不允許兩隔板置于相同空隙中。

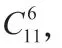
抽象數組仍需使用隔板法,只是兩隔板間距含義為使用該數字的個數,且使用數字總數確定,因此需要(6+5)個小球和5 塊隔板。
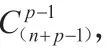
猜你喜歡
英語世界(2022年9期)2022-10-18 01:11:46
瘋狂英語·新策略(2019年9期)2019-10-17 01:51:32
瘋狂英語·新讀寫(2018年8期)2018-11-29 00:57:01
法律方法(2018年2期)2018-07-13 03:22:22
中學生數理化·八年級物理人教版(2017年10期)2018-01-22 03:04:00
中學生數理化·七年級數學人教版(2017年3期)2018-01-20 12:45:49
高中生·天天向上(2017年5期)2017-06-12 06:55:06
知識窗(2017年4期)2017-04-12 22:26:05
學生天地(2016年16期)2016-05-17 05:45:55
中國工程咨詢(2015年6期)2015-02-16 05:33:56

