電鍍金剛石線鋸鍍鎳層力學性能及磨粒把持力研究*

謝 乾, 葛培琪,2, 孟劍峰, 畢文波, 馬曉賓, 鄭楚夕, 龔 洋

(1.山東大學 機械工程學院, 濟南 250061)(2.山東大學高效潔凈機械制造教育部重點試驗室, 濟南 250061)(3.山田新材科研有限公司, 山東 臨沂 276700)

隨著半導體及光伏行業的發展，對單晶硅、多晶硅、藍寶石等貴重硬脆材料的切割加工要求越來越高。電鍍金剛石線鋸憑借耐磨性好、切削效率高、環境污染小等優點，得到廣泛的應用[1]。電鍍金剛石線鋸是采用電沉積的方法通過鍍鎳層將金剛石磨粒固結在母線基體上而獲得的。

不同于冶金學中的金屬鎳，電鍍鎳的力學性能與陰極電流密度、鍍液成分、pH值、溫度等電鍍工藝參數有關[2]。鍍鎳層的力學性能研究結果表明，鍍鎳層力學性能參數分散性較大，難以形成統一的參考[3]。但鍍鎳層材料的力學性能會影響金剛石線鋸表面磨粒的牢固程度(即鍍鎳層對金剛石磨粒的把持力)，且金剛石線鋸表面磨粒把持力的相關研究還不夠充分[4-6]。因此，采用板式試件替代金剛石線鋸基體，試驗研究了鍍鎳層的力學性能，簡約計算了鍍鎳層對金剛石磨粒的把持力，并對鍍鎳層力學參數建立了磨粒把持力有限元模型并進行了仿真分析，比較了把持力仿真與計算結果。

1 試件制備

由于電鍍金剛石線鋸直徑較細，難以直接測量鍍鎳層的力學性能，考慮到鍍鎳層的力學性能與材料內部晶粒尺寸大小密切相關，且在鍍鎳層形成的開始階段，鍍層中的結晶生長主要與基體材料屬性及表面狀態有關，基體形狀結構對鍍層力學性能影響較小，因此選用化學成分和力學性能與金剛石線鋸母線接近的T9A鋼板為電鍍試件替代金剛石線鋸基體[7-8]，制備不含金剛石磨粒的電鍍試件。試件尺寸100 mm×60 mm×40 mm。電鍍試驗方案如圖1所示。

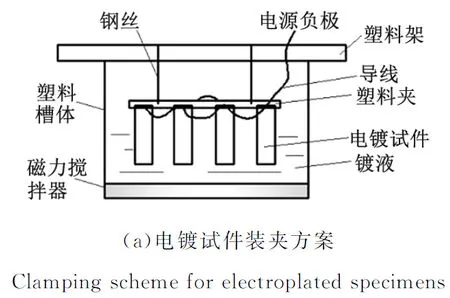
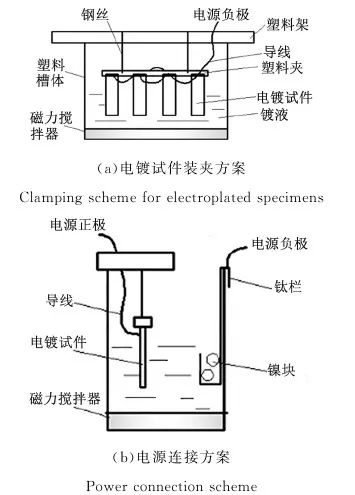
圖1 電鍍試驗方案

電鍍工藝流程為：堿洗除油→酸洗活化→鍍I層→鍍II層→鍍III層，鍍層I、II、III分別對應線鋸生產中的預鍍、上砂、加厚工序。依據工業生產中直徑65 μm電鍍金剛石線鋸的實際生產工藝參數設置電鍍試驗參數，如表1所示。試驗中控制鍍液恒溫50 ℃。本試驗共制作3組試件(每組4個)用于力學性能測試：1組(I層)，2組(I+II層)，3組(I+II+III層)。

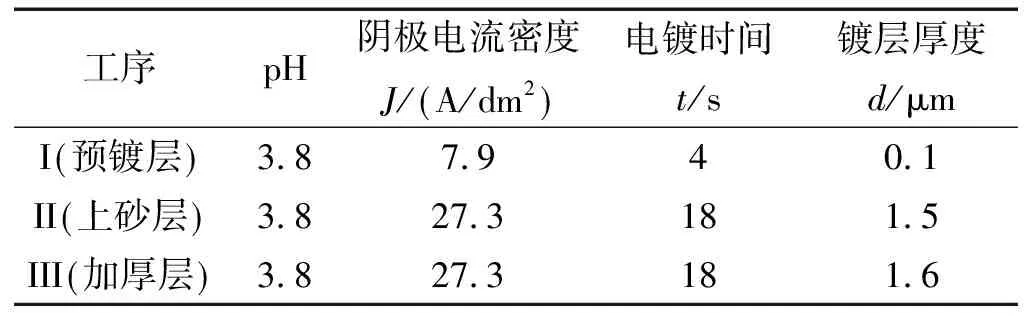
表1 電鍍試驗主要工藝參數

2 鍍鎳層力學性能測試

2.1 鍍鎳層硬度和彈性模量

采用Fischer公司的HM200S納米硬度儀測量硬度，測量時使用標準四棱錐維氏壓頭，最大載荷5 mN，加載時間5 s，試驗獲得的載荷/位移曲線如圖2所示。測量時在每個試件上分別測量4個點，取均值作為最終硬度有效值，數值如表2所示。

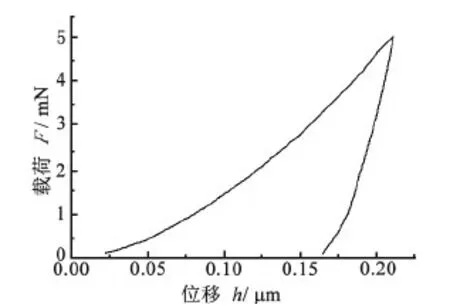
圖2 壓痕試驗載荷/位移曲線圖

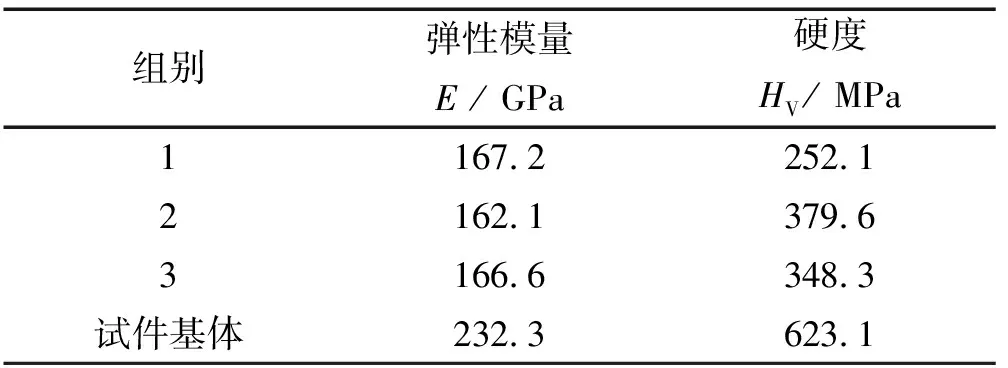
表2 硬度和彈性模量

試驗中控制金剛石壓頭的壓入深度，使其不穿透鍍鎳層，因此組1、組2和組3的測試結果分別對應I層、II層和III層的結果。由表2可知：組1的鍍鎳層硬度小于組2及組3的，產生此種現象的原因主要是電流密度的增大使得陰極電位升高，晶核成型快、成型率高；而已經成型的晶核在生長過程中受其他晶核的壓迫導致生長速度變慢，致使晶粒細化，提高了鍍鎳層硬度[2]。同時，組2的鍍鎳層硬度略高于組3的，可能是由于溶液pH升高，OH-濃度增大，導致陰極鍍鎳層中夾雜少量Ni(OH)2或堿鹽，一定程度上增大了鍍鎳層硬度[9]。但鍍鎳層厚度繼續增加，其硬度下降。

2.2 鍍鎳層殘余應力

采用X射線衍射儀測量鍍鎳層內的殘余應力。由于材料內部的殘余應力大小與晶面間距變化有關，在一定應力狀態下，應力引起的晶格應變與按彈性理論求出的宏觀應變一致，如公式[10]：

(1)

式中：1/2S2hkl和S1hkl為X射線彈性常數，(φ，Ψ)是測試方向在樣品坐標系中的方位角，σφ和εφψ分別為在該方向上測得的晶格應力和應變，σij為應力分量。在實際應用中，通常采用晶面滑移距離Dspacing表示晶格應變，Dspacing在數值上等于晶格常數C與晶格應變εφψ的乘積，單位為?。當Dspacing～sin2Ψ呈線性時，通過該直線斜率可求得應力值，當斜率為正時表示壓應力，為負時則表示拉應力[11]。

由于I層厚度很薄，易被X射線穿透導致結果不準確，故僅選取II、III組的試件進行試驗。研究采用荷蘭X 'Pert-PRO MPD型X射線儀進行測量，Dspacing～sin2Ψ圖像如圖3所示。采用線性擬合方法對測試結果進行擬合，根據擬合直線斜率計算殘余應力。II、III層的殘余應力均為壓應力，應力值分別為863.8、601.6 MPa。

此結果說明：在相同工藝參數下，較厚的鍍鎳層表面殘余應力要小于較薄的鍍鎳層的。分析產生此種現象的原因是：在電鍍初期，基體表層狀態會對鍍鎳層的結晶產生一定影響，在鍍鎳層中會存在殘余應力；隨著鍍鎳層厚度增加，基體表層對鍍鎳層的影響減弱，鍍鎳層結晶更加均勻，內部殘余應力下降[12]。

2.3 鍍鎳層與試件基體的結合強度

用板件替換線鋸母線會改變鍍鎳層與基體間的接觸面積，進而影響鍍鎳層與基體的結合力[13]。為避免接觸面積不同而產生的影響，采用結合強度指標代替結合力來評價鍍鎳層與基體的結合性能。利用劃痕法測量鍍鎳層與試件基體結合強度，其原理是利用半徑極其微小的金剛石壓頭劃傷鍍鎳層直至鍍鎳層破裂，將摩擦力突變點對應的加載力作為鍍層破裂的臨界載荷[14]。BENJAMIN等[15]給出了鍍層破斷臨界載荷和鍍層與基體結合強度間的關系：

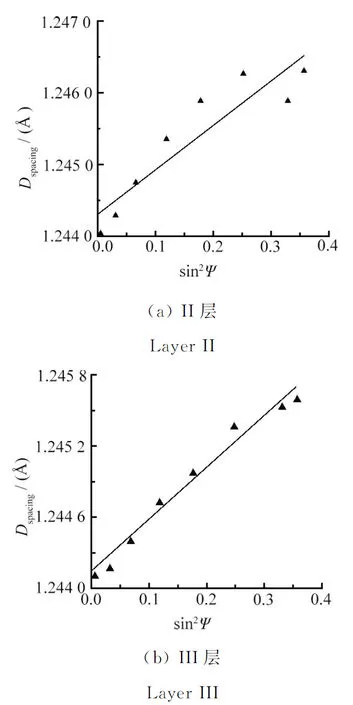
圖3 X射線測試結果

(2)

式中：τ為鍍層與基體結合強度，MPa；R為金剛石壓頭的半徑，mm；Fc為臨界載荷，N；H為基體維氏硬度，MPa；k為常數，取0.6。

使用MT-4000多功能材料表面性能試驗機分別對第1組試件進行3次劃痕試驗，用直徑0.2 mm金剛石壓頭劃擦鍍層，加載速度為50 N/min，劃痕長度5 mm。劃痕試驗的結果如圖4所示。由于此處研究的是鎳鍍層與基體間的結合強度，不包含鍍層與鍍層間的，而2、3組的電鍍工藝流程包括1組的流程，因此檢驗1組鍍層的結合強度即可。劃痕試驗試件表面形貌如圖4a所示，記錄鍍層破裂臨界載荷，得圖4b的劃痕試驗載荷圖；根據式(2)計算鍍層與試件基體結合強度，計算結果如表3所示。

由表3可知：同組內的不同試件所測得的鍍鎳層與基體結合強度存在一定差異，分析認為是試件的裝夾方式及導線連接方式存在一定缺陷，導致同組內不同試件上的電流密度存在差異，不同的電流密度會改變鍍鎳層材料屬性進而影響與基體的結合強度。另外，電鍍前的預處理可能不完善，使得基體表面存在雜質從而影響其與鍍鎳層之間的結合強度。

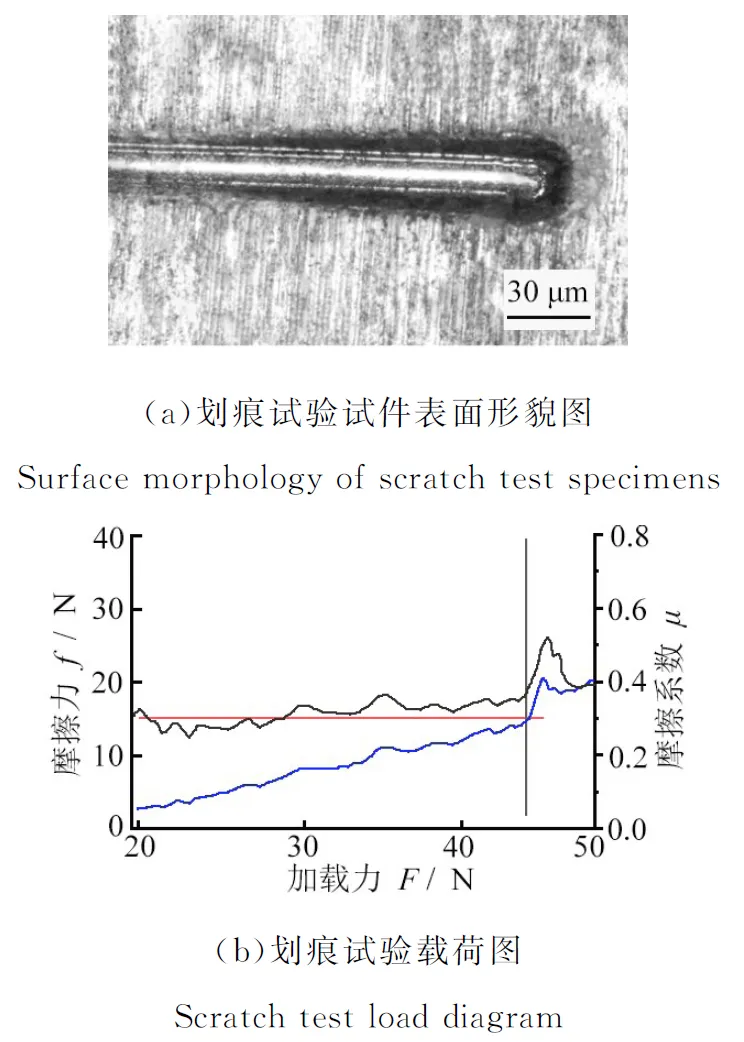
圖4 劃痕試驗過程

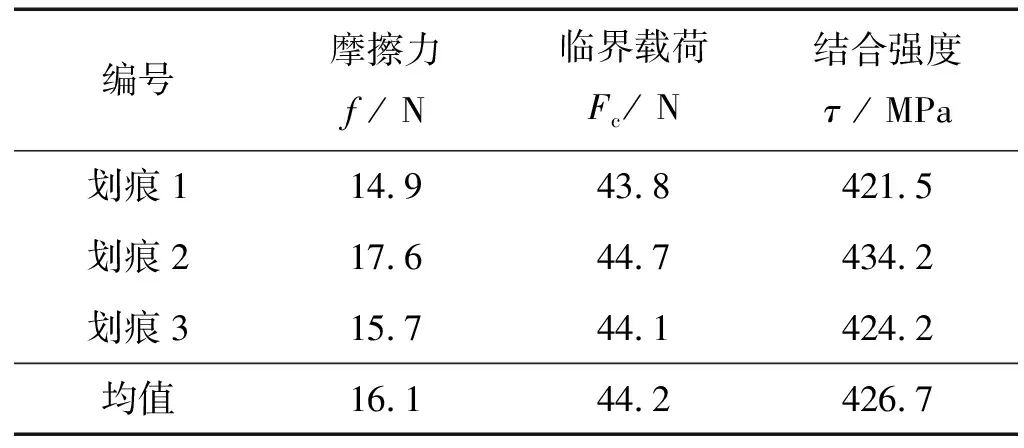
表3 鍍鎳層與試件基體結合強度

3 鍍鎳層對金剛石磨粒的把持力

3.1 磨粒把持力的簡化計算

首先采用簡化方法計算鍍鎳層對金剛石磨粒的把持力。在實際生產中，金剛石磨粒主要依靠加厚鍍層牢靠把持在線鋸上[16]，因而為了簡化分析，忽略預鍍層(I層)、上砂層(II層)的影響，只考慮加厚層(III層)的影響，因此本計算中鍍鎳層力學性能參數只按III層設置，金剛石磨粒的把持力模型如圖5所示。

圖5a的金剛石磨粒受載，對一側鍍鎳層產生擠壓并偏轉，以圖5b中的C-C’截面為例，假設鋸切力F的作用面為XOZ面，則該模型可視作無數個平面應力問題的疊加。由于鍍鎳層對金剛石磨粒把持力受法向載荷Fn影響較小[17]，為了簡化計算可忽略該力的作用。

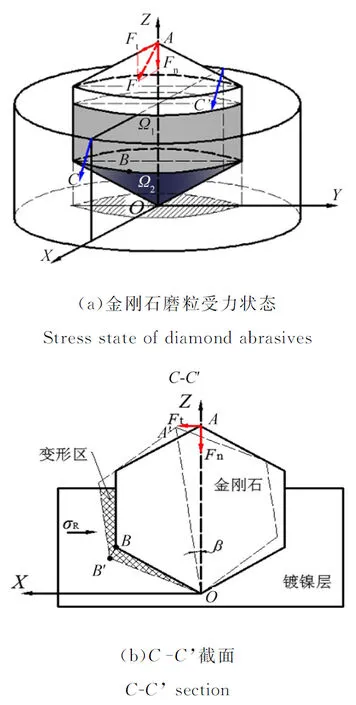
圖5 金剛石磨粒把持力計算模型

根據彈塑性力學相關知識，當鍍鎳層受擠壓發生變形時，其上某點B在任意時刻的位移Ub*(ubx*，ubz*)與應變εb*之間的關系可表示為：

(3)

式中：εbxx*、εbxz*、εbzz*分別為應變εb*沿X和Z方向的應變分量；ubx*，ubz*分別是Ub*沿X和Z方向的位移分量。

根據壓痕試驗結果可計算得出III層(加厚層)的材料本構關系[18]:

(4)

令金剛石磨粒的側面和底面分別為Ω1和Ω2，依據幾何關系，在金剛石磨粒偏轉角度β后，B點的位移分量可表示為：

(5)

式中：θ為金剛石圓錐部分半頂角；xb和zb分別為B點偏轉前位置的橫坐標與縱坐標。考慮到殘余應力σR的作用，根據試驗測得結果，將殘余應力視為沿鍍鎳層厚度呈線性分布的函數，則殘余應力在XOZ面分量為σR(XOZ)=cosθ·σR，該狀態下金剛石磨粒所受的切向載荷Ft可表示為：

(6)

根據材料脆性去除模型，金剛石磨粒所受切向載荷Ft與法向載荷Fn存在如下關系[18]：

(7)

式中：μ1為金剛石顆粒與被加工工件接觸時的摩擦系數；Kn與Kt為常數，其表達式分別為：

(8)

(9)

結合式(3)～(9)即可求出當鍍鎳層應變量達到某值時金剛石磨粒所受載荷。

依據工業生產中直徑65 μm電鍍金剛石線鋸使用的磨粒設置金剛石模型尺寸，取磨粒直徑10 μm，磨粒頂角2θ為120°，參考文獻[19]～[20]設置基體直徑100 μm，磨粒脫落時的基體臨界形變量為2%，式(7)中的摩擦系數μ1為0.2，計算得到磨粒脫落的臨界載荷值為30.23 mN。

3.2 磨粒把持力的有限元分析

為進一步分析鍍鎳層對金剛石磨粒的把持力，對金剛石磨粒把持力進行了有限元分析。當磨粒受載時，金剛石棱邊處的鍍鎳層應變量較大，當該處鍍鎳層在X軸應變分量εxx達到1%～3%，認為此時金剛石磨粒處于即將脫落的臨界狀態[20]。

建立金剛石磨粒有限元模型，設置金剛石磨粒為剛體，尺寸10 μm，基體依據式(4)給出的本構關系設置材料參數，取磨粒/基體間的摩擦系數μ1為0.1，采用C3D4線性四面體單元對金剛石磨粒有限元模型進行網格劃分，為保證分析準確度，對與金剛石接觸的基體部分也進行網格細化。

圖6是對金剛石磨粒加載后，鍍鎳層的應變沿X方向分布圖。當金剛石棱邊受壓側鍍鎳層應變εxx達到1%～3%時(圖6b)，金剛石與鍍鎳層間出現了明顯的分離現象(圖6a)，磨粒處于即將脫落的臨界狀態。提取該狀態下磨粒所受的載荷為26.51 mN，與簡化計算值30.23 mN比，有限元模擬與理論計算的結果相對誤差為-14.0%。

產生此誤差的主要原因有：(1)不同于有限元仿真，為簡化計算，理論分析時將鍍鎳層參考應變設置為定值而非區間；(2)理論計算時將金剛石磨粒視為繞O點偏轉，O點位置固定。但有限元仿真結果顯示，在鋸切力作用下，金剛石磨粒頂點處鍍鎳層產生了應變，說明頂點O在受力過程中會產生一定的位移。

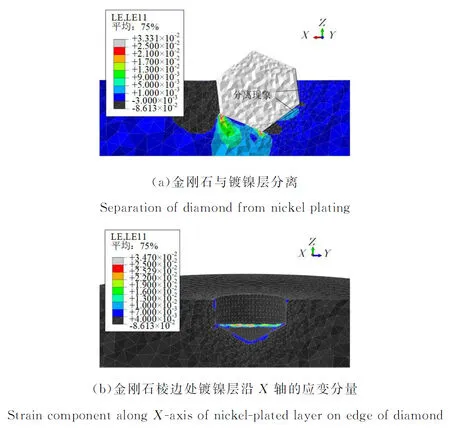
圖6 磨粒把持力有限元分析

4 結論

(1)按照金剛石線鋸電鍍工藝參數，制備了試件，通過納米壓/劃痕試驗、X射線應力分析獲得了不同電鍍工藝參數下鍍層材料的力學性能參數。

(2)依據試驗獲得的鍍鎳層力學性能參數，將鍍鎳層應變量作為衡量金剛石磨粒固結狀態的標準，簡化計算了鍍鎳層對金剛石磨粒把持力。

(3)仿真分析了鍍鎳層對金剛石磨粒的把持力，有限元仿真與簡化計算結果的相對誤差為-14.0%。