基于四階段法的軌道交通客流預測

邢 健，李 程 （上海工程技術大學 航空運輸學院，上海201620）

0 引 言

軌道交通作為一種大運量、綠色和快捷的交通方式，其建設具有投資大、工期長的特點，這就使得其前期的規劃設計顯得非常重要。通過預測軌道交通的客流，指導后續建設計劃的制定。自四階段法誕生以來，人們就廣泛通過其進行客流預測，同時也有很多學者對其進行研究和改進。楊軍等（2013） 通過建立GM-Markov 模型預測地鐵的出站大客流，并驗證該模型能較好地預測交通大客流[1]。肖穎等（2014） 通過對四階段法增加反饋機制，經過反饋和迭代，以減小誤差，實現收斂平衡[2]。丁志坤等（2017） 通過加入經濟—交通組合模型對四階段法進行優化改進，并以杭州某高速公路為例，預測其平均日交通量，該模型提高了預測的精確性[3]。Tang（2018） 提出了一種基于熵最大化理論的出租車OD 分布模型，并將該模型與重力模型進行比較，驗證其優越性[4]。葉倩文（2019） 通過SP 調查，對MNL 模型和NL 模型的適用性進行比較研究，并利用NL 模型研究地鐵和常規公交票價變化對客流的影響，證明其有較好的可靠性[5]。傳統的四階段法在客流預測時被廣泛使用，但其在實際應用中還存在某些不足，比如沒有考慮交通服務水平變量，沒有考慮交通方式之間的相關性，這明顯是不符合實際的。本文通過改進傳統的四階段法，使模型能更好地適用于軌道交通的客流預測。

1 基于四階段法的軌道交通客流預測模型

1.1 出行生成預測模型

聚類分析法將不同類型的家庭區分開，調查分析這些家庭的出行頻率，再結合預測年相應的家庭數量的預測值來預測交通量。

式中：Oi為小區i的交通發生量；Dj為小區j的吸引量；為c類家庭的出行頻率；Nci為i小區c類家庭的數量；Ad為d行業的吸引原單位；Bdi為i小區d行業就業人數。

1.2 出行分布預測模型

出行分布階段利用雙約束的重力模型預測分布交通量：

式中：ai，bj為平衡參數；f cij（）為i到j小區的交通阻抗函數，設

通過重力模型計算其交通量，可得規劃年的OD 分布矩陣。

1.3 交通方式劃分模型

根據各種交通方式適宜的出行時間、距離和準時性等，分析其相關性及競爭水平，將各種交通方式劃分成兩層：第一層包括步行、非機動車、私家車和公共交通；第二層將公共交通分為軌道交通和常規公交。

第一層采用多項Logit 模型劃分交通量。

式中：Pi為交通方式i的選擇概率；Vi為交通方式i的效用（i=1，2，3，4，…，b），分別為步行、非機動車、私家車、公共交通、軌道交通及常規公交的效用；Xi1為乘坐交通方式i的單位時間費用；Li為交通方式i的運行距離；Xi2為交通方式i的實際費用；λ 表示軌道交通與常規公交的相互取代程度的倒數；α， β 為權重參數，由于同一出行者在時間和金錢的側重點是相同的，所以各種交通方式的α 和β 值是相同的。

在第二層，計算軌道交通和常規公交選擇概率的模型為：

式中：P（r|4 ），P（b|4 ）分別為在選擇公共交通的條件下軌道交通或常規公交的選擇概率；Pr為軌道交通的選擇概率；Pb為常規公交的選擇概率。

另外，將此階段整體根據有無汽車分為兩部分，分別計算再相加求和。

通過采用NL 模型，避免了Logit 的ⅡA 特性的缺陷，具有一定的實用性。

1.4 交通分配預測模型

首先，根據路段似然值，找出有效路徑。然后，得i與j小區之間有效路徑m的選擇概率為:

式中：為從點i到點j路徑m的阻抗；為i與j小區m路徑的距離；vr為軌道交通的平均運行速度；n為換乘次數；tr為軌道交通的平均換乘時間；Φ 為出行者的實際出行時間與感知時間的判斷誤差，一般取3.0～3.5；為從點i到點j路徑m上的交通量；qij為點i到點j之間的出行分布量。

2 算 例

以某一地區為研究對象，具體調查數據如表1 至表7 所示：

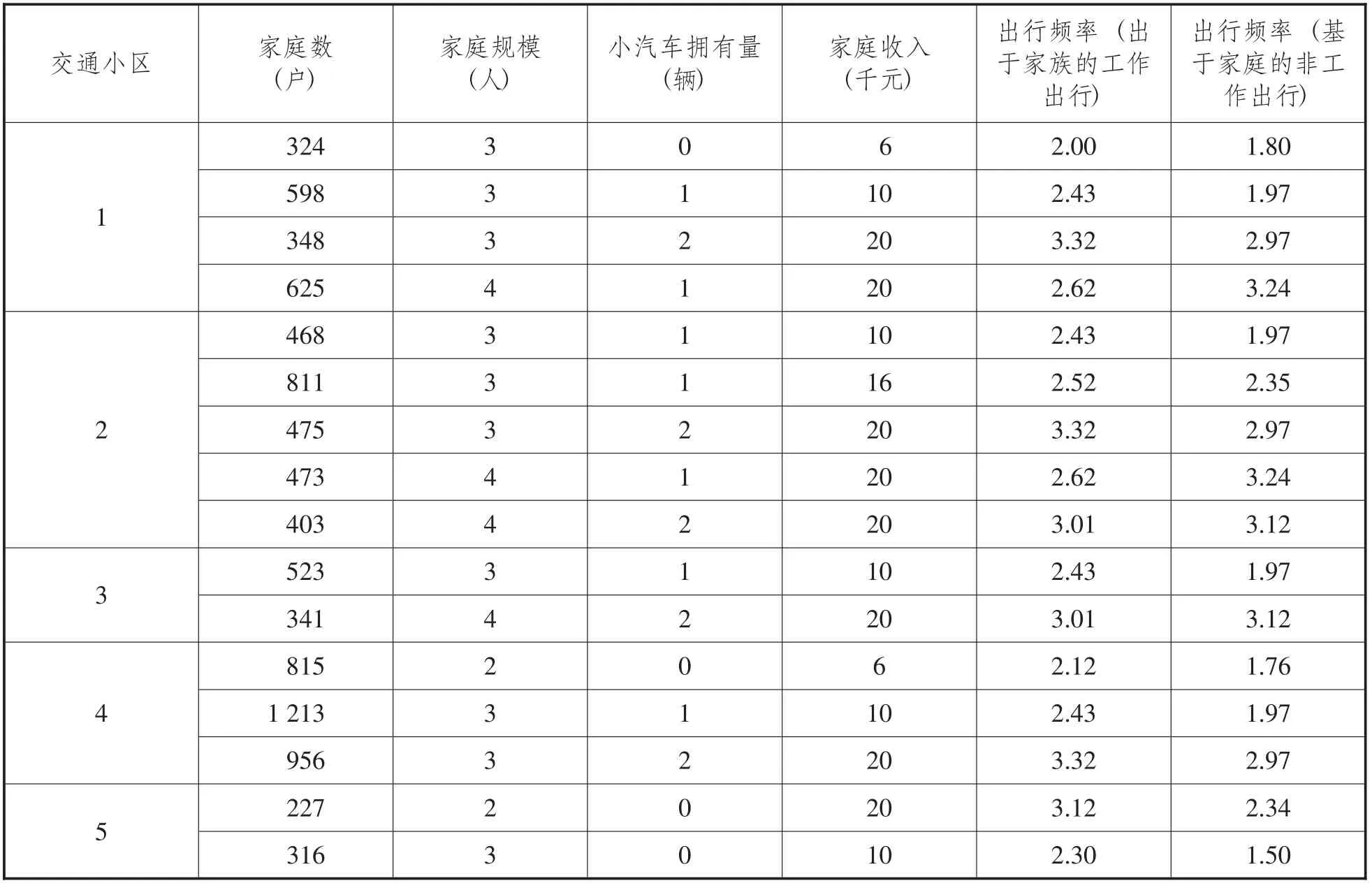
表1 各交通小區未來各種類型的家庭數

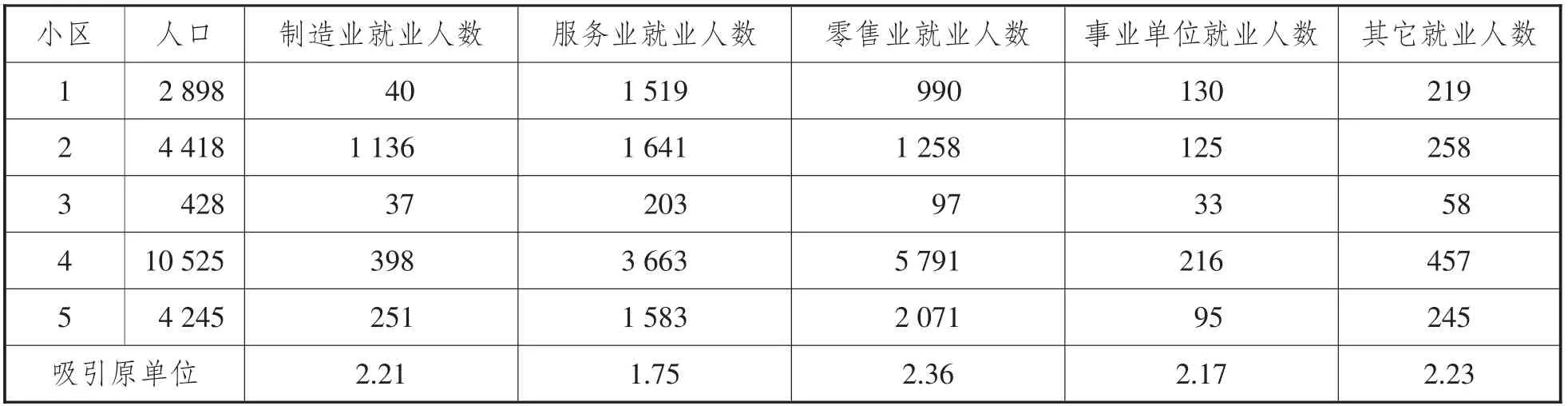
表2 各小區人口資料

表3 交通小區之間的距離 單位：km

表4 重力模型參數標定值

表5 α， β 標定值

表6 交通方式速度及費用

表7 其他參數

經過聚類分析法，雙約束的重力模型，NL 模型和隨機分配模型計算軌道交通量在線網上的分配結果如圖1 所示：

圖1 交通分配結果

3 結 論

軌道交通客流預測用于指導后續的規劃設計和建設工作。通過算例可以發現，改進的四階段法通過聚類分析法，雙約束的重力模型，NL 模型和隨機分布模型的計算，研究了交通服務水平變量和交通方式之間的相關性，科學地預測了軌道交通客流規模及其在線網上的分布情況。但是，此模型并沒有深入研究交通小區之間的相互作用，因為小區未來開發會增加其對周圍小區的客流吸引，從而增加出行量，這有待進一步優化改進。