面向O-D時變需求的城軌列車運行計劃優化方法

史 峰，涂 纖，趙 爍

(中南大學 交通運輸工程學院，湖南 長沙 410075)

城市軌道交通(簡稱城軌)線路的運行效率與服務水平在很大程度上取決于列車運行計劃。高品質的列車運行計劃通常需要權衡乘客和企業兩方面的利益，一方面為乘客提供較優質的服務，另一方面為企業降低運行成本[1]。

列車運行計劃包括列車時刻表與列車周轉方案。現有列車時刻表的研究更多地關注降低乘客出行費用，如減少乘客的候車時間[2]、換乘時間[3]和總旅行時間[4],以及優化周期性列車時刻表[5]，文獻[6]綜合考慮了乘客出行費用和企業運行成本，但這些研究均假定全天出行需求為固定常數或是均勻到達車站的理想客流。實際上，旅客出行需求具有隨時間的波動性，這種具有時間波動性的出行需求稱為時變需求[7]。文獻[8]基于客流O-D時變需求，考慮列車對數與上座率，設計了優化列車發車時間間隔的遺傳算法，降低了乘客的等待時間。文獻[9]以德國市郊鐵路為背景，強調指出需確定靈活的列車間隔以適應客流的時變性。文獻[10]和文獻[11]建立了基于彈性需求的乘客列車開行方案的雙層規劃模型，并設計了基于模擬退火算法求解的優化算法。列車時刻表的實施必須由列車周轉方案來保障[12]。文獻[13]基于給定的車輛運行時刻表，針對單車場研究了車輛調度問題。綜合優化列車運行計劃的問題非常復雜，研究成果較少。文獻[14]針對城軌線路時變斷面需求，提出了滿足服務水平的列車時刻表和列車周轉方案的兩階段優化方法。同時，文獻[15]對城軌列車運行計劃的優化具有一定的參考價值。以上文獻雖然未能有效解決面向O-D時變需求的城軌線路列車運行計劃優化問題，但是在優化思想、優化方法上有一定的啟發作用。

本文在上述文獻研究成果的基礎上，針對城軌線路的O-D時變需求，以具有單一盡頭車場的城軌線路為研究背景，提出基于列車時刻表的客流分配方法，在給定乘客服務水平的限制下，實現O-D時變需求與列車時刻表的耦合，進而以列車對數和列車車底數最小化為目標，構建了列車時刻表和列車周轉的2階段優化模型，并提出了2階段求解算法。

1 列車運行計劃優化問題

城軌線路具有m個車站s1,s2,…,sm，記全體車站集為S。車站s1至sm為線路的下行方向D，車站sm至s1為上行方向U。列車從車站su至sv的旅行時間與車站sv的停站時間之和為τ(su,sv)。端點站s1和sm的列車停放能力分別為N1和Nm(含立即折返列車)，折返作業時間分別為r1和rm。全天運營時段為[T1,T2]。

1.1 列車運行計劃

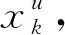
列車周轉方案主要受車場布局的影響，城軌線路上有很多種車場布局形式，每種布局形式對應不同類型的列車周轉方案。本文以單一盡頭車場為背景，討論列車時刻表與列車接續的優化問題。具有單一盡頭車場的城市軌道線路及列車運行組織形式特征如下：

線路僅有1個車場p且與端點站s1鄰接，且車場p無能力限制；若車站s1達到飽和，則新到達列車必須停放至車場p；若車站sm達到飽和，則只能等待車站sm有列車駛離后才能到達列車。

由此可見，所有早班列車均由車場p提供給車站s1，列車從車站s1出發，到達車站sm，或折返回車站s1，或停留于車站sm；列車到達車站s1后，可折返回車站sm，也可停放在車站，還可返回車場；所有晚班列車均返回車場p。

1.2 乘客服務水平

從以下3個方面來考慮乘客服務水平。

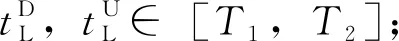
(2)發車時間間隔限制：最小發車時間間隔為τmin，最大發車時間間隔為τmax。

(3)列車載客量限制：列車載客能力為C，常規載客系數為α(0<α<1)。列車斷面載客量一般不超過αC，除非列車按最小發車時間間隔發車。當列車按最小發車時間間隔發車時，列車最大斷面載客量達到αC，但不超過列車載客能力C，超過載客能力C的需求作為車站滯留客流。

1.3 列車運行計劃優化

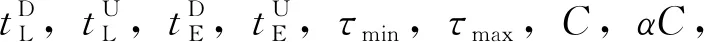
2 基于列車時刻表的客流分配

基于列車時刻表的客流分配就是模擬乘客的上車行為，根據每趟列車到達每個車站時列車上的客流量、下車人數和列車容量，計算列車在每一站的剩余能力，確定可以上車的乘客數。超過上車數量的乘客作為滯留客流，各站的滯留客流量按終點分別記錄。當需求量超過上車數量時，各終點的需求量按照等比例原則上車，以便適度體現“先到先走”的原則。

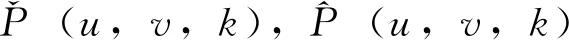
基于給定的列車時刻表，分別計算雙向各站滯留客流量和客流量。

1)下行方向

按照k=1,2,…,n;u=1,2,…,m-1;v=u+1,u+2,…,m的順序，依次遞推求解滯留客流量和客流量如下。

首先，求解滯留客流總量，即

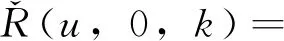
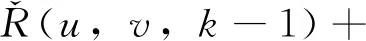
(1)

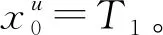
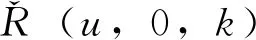
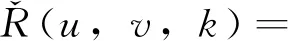
(2)

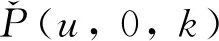
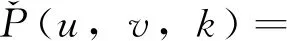
(3)

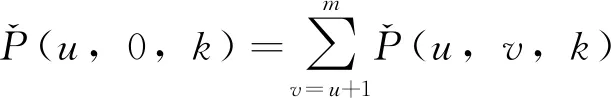
(4)

2)上行方向

按照k=1,2,…,n;u=m,m-1,…,2;v=u-1,u-2,…,1的順序，依次遞推求解滯留客流量和客流量如下。

首先，求解滯留客流總量，即

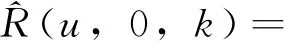
(5)

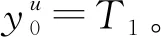
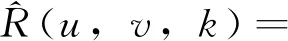
(6)

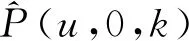
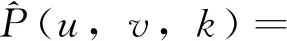
(7)

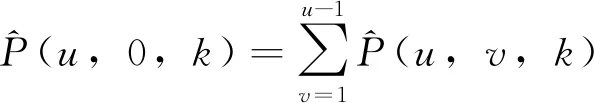
(8)

3 列車時刻表優化模型

列車發車時刻相關的約束條件如下。

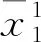
(9)

(10)

綜合考慮以上2部分內容，獲得首班車發車時間約束為

(11)

(12)

(2)末班車的最早發車時間約束。表示為

(13)

(14)

(3)最小發車時間間隔約束。同一方向發車時間間隔不得小于最小發車時間間隔，即

(15)

(16)

(4)最大發車時間間隔約束。同一方向發車時間間隔不得大于最大發車時間間隔，即

(17)

(18)

(5)列車在各站發車時間與始發時間的關系

由于τ(s1,su),τ(sm,su)分別表示列車在區段(s1,su),(sm,su)的旅行時間與車站su的停站時間之和，所以滿足如下關系。

(19)

(20)

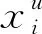
(6)無車場端車站sm列車接續約束。第i趟上行列車出發前，第i趟下行列車必須到達車站sm。由于τ(s1,sm)表示列車在區段(s1,sm)的旅行時間與車站sm的停站時間之和，rm為車站sm的折返作業時間，所以

(21)

(7)無車場端車站sm停車能力約束。第i趟下行列車到達車站sm之前，第i-Nm趟上行列車必須離開車站sm。由于τ(s1,sm)表示列車在區段(s1,sm)的旅行時間與車站sm的停站時間之和，rm為車站sm的折返作業時間，所以

(22)

(8)出行需求與列車始發時間的耦合。若按最小發車時間間隔發車，則列車最大斷面載客量達到常規載客能力αC，但不超過最大載客能力C；否則，列車斷面載客量不超過常規載客能力αC。即

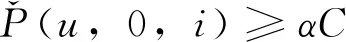
(23)

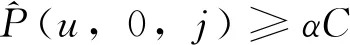
(24)

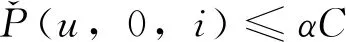
(25)

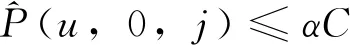
(26)

以列車對數n最小化為優化目標函數，以上述關系式為約束條件，構建列車時刻表的優化模型為

minZ=n

(27)

s.t.

約束條件式(1)—式(26)。

4 列車時刻表優化算法

4.1 算法思想

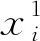
將求解步驟分為3步：最大化首班車發車時間、最大化中間列車發車時間、終止條件。

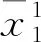
(28)

(29)

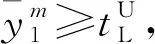
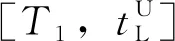
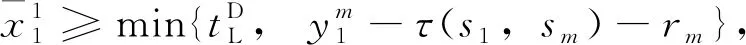
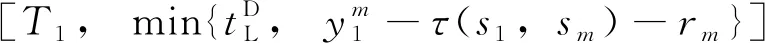
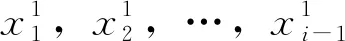
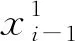
對于下行方向，分別考慮以下3種情形。

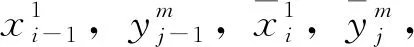
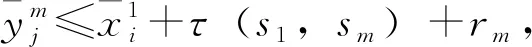
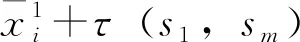
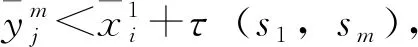
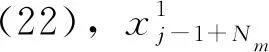
3)終止條件

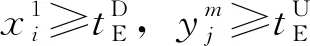
根據上述算法思想和相應步驟，設計模型式(1)—式(27)的求解算法。

4.2 列車最晚發車時間的雙向關聯序列化優化算法

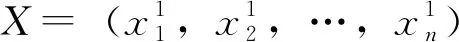
開始

i←2,j←2；

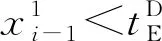
開始1

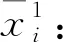
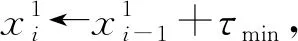
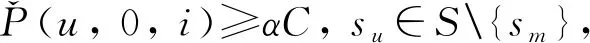
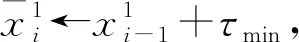
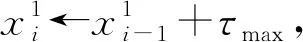
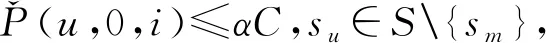
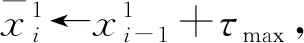
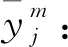
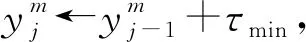
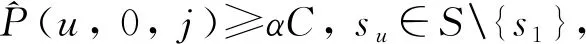
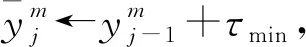
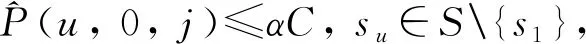
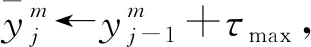
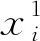
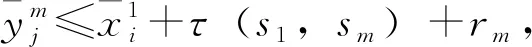
i←i+1,j←j+1}；

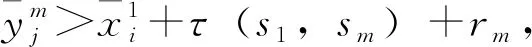
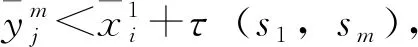
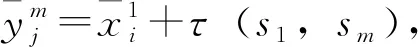
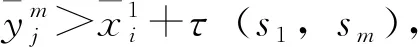
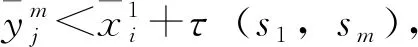
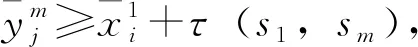
j←j+1}；

返回1

i←i-1,j←j-1；

n←i；

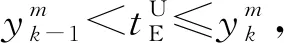
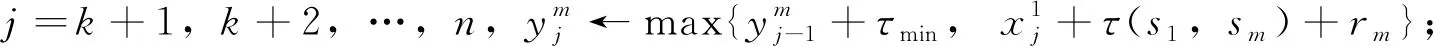
結束。

5 列車周轉方案優化方法

5.1 列車周轉方案優化模型

車站s1始發的下行列車車次序集為{i|i=1,2,…,n}，終到的上行列車車次序集為{j|j=1,2,…,n}，列車周轉問題就是要確定這2個方向列車車次的銜接關系。每1趟始發的下行列車，或者由此前到達的上行列車來擔當，或者由來自車場p的列車來擔當。我們采用指派問題描述列車周轉問題。

借助于指派問題優化求解列車周轉問題，就是優化{j|j=1,2,…,n}與{i|i=1,2,…,n}之間的指派M。指派滿足以下限制：M?{(j,i)|j,i=1,2,…,n}， 對于任何(j,i), (j′,i′)∈M，滿足若j=j′，則i≠i′；若i=i′，則j≠j′。對于任何j=1,2,…,n,i=1,2,…,n,定義指派費用cji如下。

(30)

式中：K為充分大的數，通常取K=24nh。

定義指派變量

(31)

可建立列車周轉問題的指派模型為

(32)

s.t.

(33)

(34)

xji=0, 1j，i=1,2,…,n

(35)

指派模型的式(30)—式(35)以接續時間最小化為優化目標，等價于不可接續車次數量最小，全部列車運用小時數最小，進而列車車底數最小。

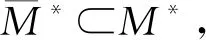
(36)

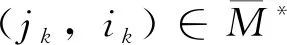
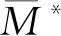
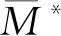
5.2 列車周轉方案優化算法

匈牙利算法可以用來求解指派問題的最優解。采用匈牙利算法對建立的指派模型進行求解，算法分為以下2步。

第1步：用匈牙利算法求解指派問題最優解的方法求解最優指派方案M*。

6 算例分析

以北京市地鐵5號線為例，對本文的方法進行驗證。該線路上共23個車站，如圖1所示，天通苑北—宋家莊為下行方向，天通苑北站有太平莊車輛段。列車在立水橋、大屯路東、惠新西街南口、雍和宮、東四、東單、磁器口、蒲黃榆站的停站時間為45 s，其它車站停站時間為30 s。區間運行時間參考首班列車各站發車時間與停站時間推算出，

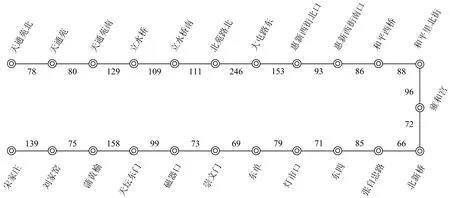
圖1 車站及區間運行時間(單位：s)

采用該線2014年某天的實際乘車O-D客流數據作為時變需求，篇幅所限，不詳細列舉。為了增加客流需求強度，將該O-D客流需求放大2倍作為算例的O-D客流需求。

利用優化方法求出列車運行計劃如圖2所示，圖中車站s1與車站sm之間的線段為列車運行線，簡略起見，沒有標記沿途停站的時間信息。車站s1與車站sm外側的折線表示列車的接續關系。車站s1外側的實心箭頭表示列車來自或返回車場，空心箭頭表示列車在車場接續，以解決車站s1不滿足停放能力N1的困難。D與數字的組合表示下行方向列車車次，U與數字的組合表示上行方向列車車次，為避免車次標記過于密集，車次標記間隔大約為10趟列車。

優化產生的列車運行計劃，開行列車194對，需要列車62列，列車接續時間為850.36 min，往返車場124次。

從圖2可以看出，在早晚高峰具有較密集的列車開行頻率，發車時間間隔隨著客流需求變化而變化，具有較平滑的變化規律。下面分別對折返站列車接續狀態、發車時間間隔、主導方向成因分析如下。

1)折返站列車接續狀態

為了分析折返站sm的列車接續狀態，從圖2可以看出：列車接續狀態大體可分為3個階段，第1階段為立即折返，第2階段為停車能力持續飽和，第3階段為立即折返。

比較雙向列車在折返站sm的始發終到時刻發現：

下行列車1至36與上行列車1至36均由立即折返的方式接續，即接續時間均為折返作業時間rm=2 min。下行列車37與上行列車37的接續時間超過折返作業時間rm，此后，接續時間不斷增加，折返站sm開始停放暫時不需要的列車，停車能力飽和率越來越大。

圖2 城軌線路列車運行計劃示意圖

上行列車44的發車，釋放了折返站sm處于飽和的停車能力，保證下行列車46能夠終到車站sm(依據如下：下行列車46的終到時間等于上行列車44的始發時間，但下行列車45的終到時間大于上行列車43的始發時間)。此后，折返站sm進入了停車能力持續飽和狀態。

下行列車104的終到，終止了停車能力持續飽和狀態(依據如下：下行列車104的終到時間略小于上行列車102的始發時間，但下行列車103的終到時間等于上行列車101的始發時間)。此后，車站sm的停車能力飽和率越來越小，進而變得完全不飽和，折返時間越來越短，直至下行列車112與上行列車112仍然不是按照立即折返的方式接續。下行列車113至194與上行列車113至194均由立即折返的方式接續。

立即折返與停車能力持續飽和分別表示不同方向的需求主導。立即折返意味著上行方向為主導方向，即上行方向按上行需求開行列車，下行方向為上行方向及時提供列車。折返站停車能力持續飽和意味著下行方向為主導方向，即下行方向按下行需求開行列車，上行方向為下行終到折返站而及時釋放停車能力。

2)發車間隔時間

為了分析發車間隔時間，將上下行2個方向相鄰列車發車間隔時間變化規律如圖3所示。圖中第i個藍色菱形標記下行列車i與下行列車i+1的發車間隔時間，第j個紅色加號標記上行列車j與上行列車j+1的發車間隔時間。

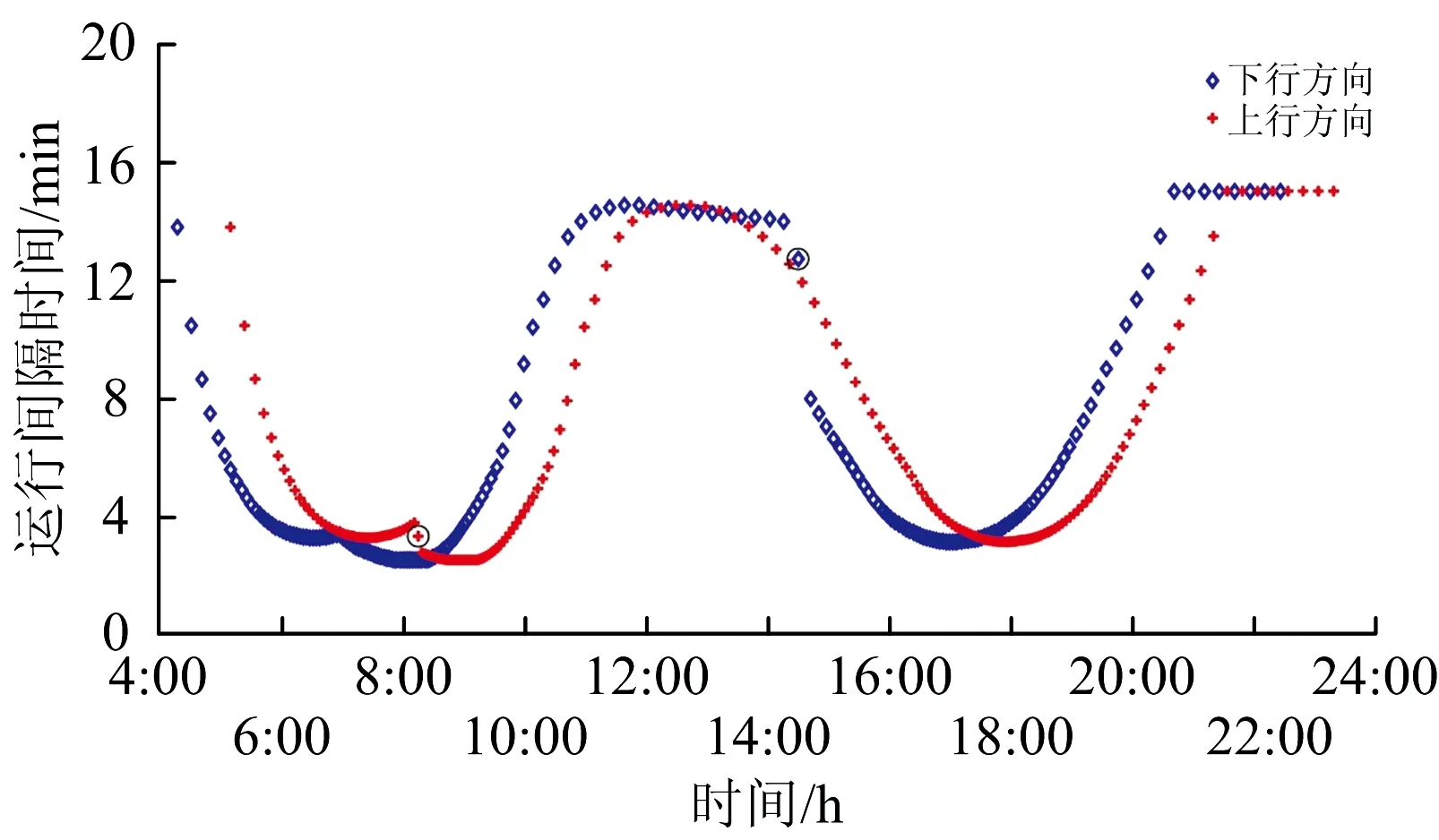
圖3 列車運行間隔時間示意圖

從圖3可以看出：對于列車i=1,2,…,36，與列車i+1的發車間隔時間曲線，上下行方向的變化規律完全一致，只是下行方向提前了τ(s1,sm)+rm=53 min 5 s，這是由上行方向主導的原因所致。

上行方向在這一階段的主導地位結束于下行列車37的終到，下行方向需求加大，發車間隔時間變小，下行列車發車間隔時間曲線出現了1個折點，但上行列車的發車間隔時間仍然在增加。直至上行列車43的終到，上下行分別按照各自需求確定發車間隔時間，密集到達、暫不需要的下行列車可以停放在折返站sm備用。

上行列車43與44的發車間隔時間有1個突變，就是圖3中被圓圈所包圍加號對應的孤立點，此時上行列車44必須發車，以釋放折返站sm處于飽和的停車能力，保證下行列車46能夠終到車站sm。此后上行列車i的發車時刻與下行列車i+2在折返站sm的終到時刻保持相等，體現了下行方向的主導地位，致使上行列車的發車間隔時間與下行列車的發車時間間隔保持一致。

下行方向在這一階段的主導地位結束于下行列車104的終到，上行方向需求加大，發車間隔時間大幅下降，但下行列車的發車間隔時間仍然緩慢下降。直至下行列車112的終到，上下行分別按照各自需求確定發車間隔時間，上行列車出發較下行列車到達的列車缺額，由折返站sm停放的列車填補。

下行列車112與113的發車間隔時間有1個突變，就是圖3中被圓圈所包圍菱形符號對應的孤立點，此時下行列車113必須到達折返站sm，以立即折返的接續方式擔當上行列車113，保證上行列車113能夠準時始發。此后下行列車的發車間隔時間與上行列車的發車間隔時間保持一致，體現了上行方向的主導地位。

3)主導方向成因

各個階段主導方向的成因與需求大小相關，與折返站沒有車場也相關。折返站沒有車場導致上行列車k比下行列車k的需求滯后約1 h，使得上下行需求大小必須進行錯位比較。由此分析3個階段的主導方向成因如下。

在第1階段，下行列車更接近于早班低谷，上行列車更接近于早高峰，可見上行列車的需求更大一些，所以上行方向為主導方向。

在第2階段，下行列車更接近于早高峰，上行列車更接近于中午低谷，可見下行列車的需求更大一些，所以下行方向為主導方向。

在第3階段，階段前期，下行列車更接近于中午低谷，上行列車更接近于晚高峰，可見上行列車的需求更大一些，所以上行方向為主導方向。階段后期，由于上行方向晚高峰持續時間更長一些，所以一直保持上行方向為主導方向。在晚班期間，上下行列車都按照最大間隔時間τmax=15 min發車，自然也都是立即折返了。

綜上所述，折返站列車接續狀態、發車間隔時間和各階段的主導方向成因都反映了列車運行計劃具有顯著的合理性，這得歸功于結合客流分配和服務水平優化列車運行計劃，使得列車運行計劃與乘客出行需求的吻合度高，列車開行趟數和車底數量最小化。

7 結 論

(1)城軌線路列車運行計劃優化問題可以描述為基于服務水平的列車時刻表和列車周轉2階段優化問題，最小化開行列車對數和列車車底數，優化有車場端列車接續關系。對于給定的列車時刻表，關于O-D時變需求的客流分配可以通過遞推公式獲得，由此可實現客流需求與列車時刻表的耦合。

(2)針對具有單一盡頭車場的城軌線路，在無車場端的列車接續和停車能力約束下，結合O-D時變需求的客流分配，可采用序列化優化方法，分步實施最大化列車發車時間，實現雙向列車時刻表關聯優化。

(3)基于最優列車時刻表，將有車場端的列車周轉問題描述為指派問題，一個指派模型可同時確定端點站的列車最優接續關系、往返于車場的列車。

(4)具有單一盡頭車場的城軌線路的列車運行計劃，上行方向發車間隔時間比下行方向發車間隔時間的變化規律滯后。在上行方向為主導的時間段，滯后稍大；在下行方向為主導的時間段，滯后稍小。