偏心受壓構件承載力計算問題探討

飛俊杰 蔣 源

(云南水利水電職業學院，云南昆明 650499)

在實際工程中，偏心受壓構件應用非常廣泛，工業廠房排架柱和框架頂層邊柱往往屬于大偏心受壓，高層建筑的下部幾層往往屬于小偏心受壓。其中矩形截面偏心受壓構件最為基礎和常見，正確地對其受力分析、承載力計算、合理地選擇配筋形式，是設計者經常要面對的一個問題，恰當的分析和計算將會給建設減少不必要的工程投資。

1 偏心受壓構件計算理論

1.1 計算假設

為簡化計算，正截面承載力計算基于《混凝土結構設計規范》［1］(以下簡稱《規范》)的基本假設:

1)平截面假設。正截面變形后仍保持平面。

2)不考慮受拉區混凝土的抗拉強度。

3)混凝土受壓區的應力與應變關系理想化，當采用強度等級C50及以下混凝土時，混凝土壓應變εcu=0.003 3，縱向鋼筋的極限拉應變εy=0.01。

4)縱向鋼筋的應力取鋼筋應變與其彈性模量的乘積σs=εsEs，但其絕對值不大于其相應的強度設計值σs≤fy。

1.2 大小偏壓基本判別

偏心受壓構件的受力可按大偏心受壓與小偏心受壓兩種受力狀態進行分析。大小偏心受壓的基本判別方法是通與界限相對受壓區高度ξb比較判別，當ξ≤ξb時，截面屬于大偏心受壓狀態;反之當ξ＞ξb時，則屬于小偏心受壓。

1.3 基本計算公式及限制條件

基于計算假設，根據大偏心受壓計算受力圖1，用力平衡方程寫出其計算公式:

其中，e=ei+0.5h－as。

公式適用條件:

1)保證破壞時受拉鋼筋先屈服:ξ≤ξb。

2)保證破壞時受壓鋼筋應力能達到屈服:x≥2a's。

若x≥2a's，取x=2a's，這時混凝土抗壓力與受壓鋼筋A's抗壓力共線，對受壓鋼筋合理點取矩有:

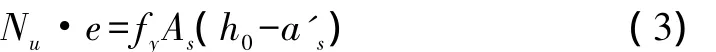
同理，根據小偏心受壓計算受力圖2，用力學平衡方程寫出小偏心受壓計算公式。

圖1 受力圖（一）

圖2 受力圖（二）

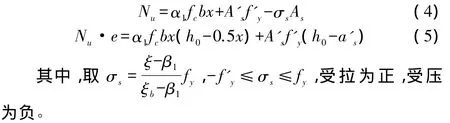
2 不對稱配筋計算

在進行不對稱配筋偏心受壓構件正截面設計時，無法求出ξ的大小，因此上述基本判別方法無法使用。根據工程經驗，通常按初始偏心距 ei的大小進行判別，當 ei＞0.3h0時，可初步按大偏心受壓進行計算;當 ei≤0.3h0時，可初步按小偏心受壓進行計算。但最終還需要根據基本判別方法校核。

2.1 大偏心受壓截面設計問題

若ei＞0.3h0，一般可按大偏心受壓計算。分別有以下兩種情況:

情況1:A's，As均未知。兩個基本公式對應三個未知數A's，As，x，故無唯一解，為保證鋼筋用量最省，即 min(A's+As)，充分發揮混凝土抗壓能力，故取x=ξbh0。

計算時，用式(2)求出A's;然后用式(1)求出As。

情況2:A's已知。兩個基本公式對應兩個未知數As，x，有唯一解。

計算時，先用式(2)求出受壓區高度x。

1)當 2a's≤x≤ξbh0，用式(1)計算 As;

2)當 x＜2a's，取 x=2a's，用式(3)計算 As;

3)當x＞ξbh0，應改用小偏心受壓重新計算;如果不改變截面尺寸或不提高混凝土強度等級，仍按大偏心類型計算，說明受壓區鋼筋A's配量不足，按A's，As，x未知類型重新計算。

2.2 小偏心受壓截面設計問題

若ei≤0.3h0時，按照小偏心受壓情況計算，兩個基本方程對應三個未知量A's，As，x，故無唯一解。在一般情況下，小偏心受壓破壞時，遠離軸壓側鋼筋As無論受拉、受壓都無法屈服，當軸壓力N≤α1fcbh時，按照《規范》規定的最小配筋率取值As=0.2%bh;當軸壓力N＞α1fcbh時，應該 驗 算 反 向 破 壞 的 承 載 力［2］，取 As=max

按小偏心受壓計算式(4)，式(5)，可求出ξ，根據相對受壓區高度ξ不同值，對應有以下三種情況:

1)若 ξb＜ξ≤2β1－ξb時，破壞時遠離軸壓力一側鋼筋 As不論拉、壓均未屈服。這時將ξ代入小偏壓計算公式計算出A's;

2.3 偏心受壓構件截面復核問題

2.3.1 彎矩作用平面的承載力復核

彎矩作用平面的承載力復核有兩種情況:

1)給定軸力N，求彎矩作用平面的彎矩設計值M;

取 x=xb= ξbh0代入式(1)，有 Nb= α1fcbξbh0+f'yA'sfyAs。若N≤Nb，為大偏心受壓，由式(1)求出受壓區高度x，再用式(2)求出 e，根據 e=ei+0.5－as求出 ei，再由 ei=e0+ea確定 e0，從而有 M=Ne0;若 N＞Nb，為小偏心受壓，由式(4)求出受壓區高度x，再用式(5)求出e，之后步驟同上述大偏心受壓一致。

2)給定軸力作用的偏心距e0，求軸力設計值N;

對豎向作用點取矩求受壓區高度x。若x≤xb，為大偏心受壓，再由式(1)求出N;若x＞xb為小偏心受壓，聯立式(4)，式(5)求出 N。

2.3.2 垂直于彎矩作用平面的承載力復核

無論是截面設計或截面復核問題，是大偏心受壓還是小偏心受壓，都應根據長細比，確定穩定系數φ，按軸心受壓的情況式(6)，驗算垂直于彎矩作用平面的受壓承載力。

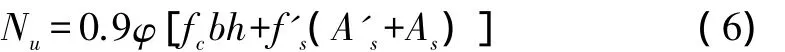
3 對稱配筋計算

在實際工程中，偏心受壓構件在不同內力組合下，可能有反向的彎矩，采用對稱配筋使設計偏于安全。同時對稱配筋還可以避免施工差錯，裝配式柱為保證吊裝不出錯，一般采用對稱配筋。對稱配筋即:A's=As，fy=f'y，as=a's。

3.1 對稱配筋截面設計

對稱配筋時，把A's=As代入式(1)，有:

當ξ≤ξb時，按大偏心受壓構件設計。計算時又有以下兩種情況:

2)若 x＜2a's，取 x=2a's，用式(3)計算 As。

當ξ＞ξb時，按小偏心受壓構件設計。聯立式(4)，式(5)，有:

這時需解關于ξ的一元三次方程，為使計算簡化，根據《規范》取 ξ(1－0.5ξ)=0.43，把式(8)簡化為關于 ξ的一元，進而求出A's。

3.2 對稱配筋截面復核

其截面復核計算同不對稱配筋情況一致，不再累述。

4 計算探討

在解決偏心受壓構件承載力計算時，除了滿足計算公式要求外，還需保證計算結果符合構造要求，同時還要理解計算時出現的各類特殊情況的意義及解決方法，設計時在安全可靠和工程造價間找到平衡點。

4.1 大偏壓計算時受壓區鋼筋負值情況

在實際設計中截面尺寸較大的構件在大偏心受壓計算時，經常會出現A's＜0的情況［3］，這是因為受壓區的混凝土的抗壓強度有富余，不需受壓鋼筋。針對這種情況，可按最小配筋取A's=0.2%bh，進而計算As時，但所求x大概率出現x＞xb的情況，應按小偏心受壓處理;如若要按大偏心受壓計算，可以采用對稱配筋的方式取A's=As進行求解。

4.2 配筋方式

通過文獻［4］計算對比，可知對稱配筋的鋼筋總面積都比非對稱配筋總面積要大，但對稱配筋形式計算簡單、便于操作、偏于安全。非對稱配筋能夠充分利用材料強度，經濟效益高。所以在實際工作中，需根據不同的情況和需求采用相適應的方法，在保證構件安全可靠的同時需考慮節約鋼筋用量，降低工程成本。

4.3 計算流程

偏壓構件截面計算問題內容多、概念多、公式多，且情況復雜。但經過分析整理，可把問題歸結為“作受力圖→列力的平衡方程→按最優設計補充方程(若需要)→求解方程(進行相應簡化，避免求解3次方程)→滿足構造要求”［5］。

5 結語

通過矩形截面偏心受承載力計算問題的論述，對計算中可能出現的特殊情況進行解釋說明，對處理各類計算的方法進行詳細介紹，對不同配筋方式進行比較，同時總結歸納整個計算問題的核心思想和流程，能夠幫助結構設計人員更好地理解和應用相關知識。