基于類圖像處理與向量化的大數據腳本攻擊智能檢測

張海軍,陳映輝

(嘉應學院 a.計算機學院; b.數學學院,廣東 梅州 514015)

0 概述

隨著互聯網、云計算、物聯網、大數據等技術的快速發展以及數以萬計網絡接入點、移動終端和網絡應用的出現,產生了大量蘊含較高價值的大數據,這給網絡空間安全帶來了前所未有的挑戰。從服務器交易系統的數據庫數據到各終端業務的系統數據,如各種流水操作、網購記錄、網絡瀏覽歷史、播放的音視頻、微博和微信等基于移動或Web應用的數據等,使得基于Web應用的攻擊逐漸成為網絡中的主要攻擊,如跨站腳本(Cross-Site Scripting,XSS)攻擊[1],其表現為:網絡釣魚,盜取用戶的賬號和密碼;盜取用戶Cookie數據,獲取用戶隱私,或者利用用戶身份進行進一步操作;劫持瀏覽器會話,從而冒充用戶執行任意操作,如非法轉賬、強制發表博客;強制彈出頁面廣告,刷流量;進行惡意操作,如纂改頁面信息、刪除文章、傳播跨站蠕蟲腳本、網掛木馬;進行基于大量客戶端的攻擊,如DDOS攻擊;聯合其他漏洞(如CSRF);進一步滲透網站。

傳統的計算機病毒檢測方法主要利用病毒特征庫中的已有特征,通過提取相應樣本的特征,在病毒庫中搜索并比較是否存在相匹配的特征,從而確定病毒是否存在。這種方法主要基于已知的病毒進行檢測,難以發現新的病毒,特別是對于變形病毒其更加無能為力,而且針對大數據問題時效率較低。當前安全防護措施已經由過去的“80%防護+20%檢測及響應”變成了“20%防護+80%檢測及響應”。深度學習以其強大的自適應性、自學習能力在語音、圖像、自然語言處理等方面取得了比傳統機器學習方法更好的效果,特別是在解決大數據問題時,其效果更好。

本文借鑒類圖像處理過程，設計一種基于神經網絡的詞向量化算法，對訪問流量語料庫大數據進行詞向量化處理，通過理論分析和推導實現多種不同深度的深層卷積神經網絡算法，從而對大數據跨站腳本攻擊進行智能檢測。

1 語料大數據處理及向量化

Web入侵檢測本質上是基于日志文本的分析[2],即對訪問流量語料大數據進行分析。首先,進行自然語言處理,由于當前基于安全防護的語料樣本比較缺乏,標注好標簽的樣本更少,因此需要進行數據處理和建模,具體為:1)語料獲取;2)語料預處理,包括清洗、分詞、詞性標注、去停用詞;3)初級數據分析,如URL參數個數、字符分布、訪問頻率等分析。其次,進行詞向量化,將詞映射到向量空間,在計算機中,任何信息都是以0和1的二進制序列表示,如所有的字符(包括字母、漢字、英語單詞等語言文字)都有一個編碼。本文將大數據日志文本轉換成數值數據并以矩陣表示,再基于詞向量方法進行數據處理和分析,即將攻擊報文轉換成類似于圖像數據(像素)的矩陣,也將字符串序列樣本轉換成具有一定維度值的向量,再對詞向量進行數值化的特征提取和分析,如數據抽樣、矩陣相關性維數約減、特征提取、降維、聚類等運算。最后,進行模型訓練與數值分析,實現用戶行為分析、網絡流量分析和欺詐檢測等。上述過程原理如圖1所示,向量化處理過程詳見3.1節實驗部分,其實現了語料大數據的獲取、處理、建模、分詞和詞向量化等[3]。

圖1 大數據跨站腳本攻擊智能檢測原理Fig.1 Intelligent detection principle of big data cross-site scripting attack

2 算法設計

2.1 詞向量化算法設計

利用CBOW實現詞向量,即已知上下文詞語來預測當前詞語出現的概率。為此,需要最大化對數似然函數:

(1)

其中,w表示語料庫C中的詞。式(1)可以看作多分類問題,因為多分類是由二分類組合而成,所以可以使用Hierarchical Softmax方法進行求解。先計算w的條件概率,如下:

(2)

(3)

其中,σ(x)為sigmoid函數。由于d只取0和1,因此式(3)可以以指數的形式表示為:

(4)

將式(4)代入式(1)可得:

(5)

式(5)中的每一項可以記為:

(6)

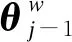
(7)

令σ′(x)=σ(x)[1-σ(x)],代入式(7)可得:

(8)

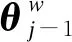
(9)

(10)

由于Xw是上下文的詞向量之和,在處理時將整個更新值應用到上下文每個單詞的詞向量上。

(11)

基于上述算法建立模型,將原始語料作為輸入,即可實現語料數據的詞向量化。

2.2 深度卷積神經網絡算法設計

在計算機視覺[4]、自然語言處理[5]等領域,相對于傳統神經網絡或其他ML算法,深度卷積神經網絡(Deep Convolutional Neural Networks,DCNNs)具有更高的識別率、更強的魯棒性以及更好的泛化性能[6]。為此,本文設計多種DCNNs算法,構建基于“輸入層+卷積層+卷積層+池化層+卷積層+卷積層+池化層+全連接層+全連接層+Softmax層”10層深度的結構,以實現大數據安全防護檢測,并通過模型訓練進行大數據智能檢測。為減輕梯度消失等問題[7-8],本文選擇Relu函數作為激活函數,其定義為:

f(x)=max(0,x)

(12)

通過式(13)可以求得卷積層的相應輸出值,如下:

(13)

其中,xi,j表示向量的第i行第j列元素值,wm,n表示卷積核第m行第n列的權值,wb表示卷積核的偏置項,F是卷積核的大小(寬度或高度,兩者相同)。卷積運算后得到下一特征層,其寬度和高度分別為:

(14)

其中,W1和H1分別表示卷積前向量的寬度和高度,W2和H2分別表示卷積后Feature Map的寬度和高度,P表示在向量周圍補0的圈數值,S表示卷積運算時的步幅值。卷積前向量的深度可以大于1,如表示為D,則相應卷積核的深度也必須為D,可以求得卷積后的相應輸出值。

(15)

對于池化層和全連接層,輸出運算相對簡單。

在DCNNs進行訓練時,先利用鏈式求導計算損失函數對每個權重的梯度,然后根據梯度下降公式更新權重。具體過程如下:

1)對于卷積層誤差項的傳遞,假設步長S、輸入深度D和卷積核個數均為1,它們間的關系如下:

(16)

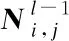
(17)

(18)

(19)

可以將式(19)寫成如下的卷積形式:

δl-1=δl*Wl°f′(Nl-1)

(20)

其中,符號°表示將矩陣中的每個對應元素相乘。當步長S、輸入深度D和卷積核個數均大于1時,同理可得:

(21)

2)對于卷積核權重梯度,由于權值共享,根據全導數公式可得:

(22)

即用sensitive map作卷積核,對輸入進行交叉相關cross-correlation運算。

3)基于上述分析計算,得出偏置項的梯度:

(23)

即偏置項的梯度是sensitive map所有誤差項之和。獲得所有的梯度之后,根據梯度下降法可以更新每個權值,從而實現卷積層訓練。

對于池化層,一般有max pooling和mean pooling 2種,它們不用計算梯度,只需將誤差項傳遞到上一層。通過分析可知,對于max pooling池化,下一層的誤差項會按原值傳遞到上一層最大值對應的神經元,其他神經元的誤差項為0;對于mean pooling池化,下一層的誤差項會平均分配到上一層對應區塊的所有神經元,即可以用克羅內克積實現池化:

(24)

其中,n表示池化層核的大小。

由此,利用已實現的卷積層和池化層結合全連接層,可以堆疊形成DCNNs[9],從而完成大數據腳本攻擊的智能檢測[10]。

3 實驗結果與分析

3.1 實驗大數據

3.1.1 語料大數據獲取

用于本文實驗的大數據包括兩類[11-12]:正樣本大數據(帶有攻擊行為),利用爬蟲工具從網站http://xssed.com/爬取獲得,由Payload數據組成;負樣本大數據(正常網絡請求),為體現特殊性和普遍性,共收集了2份數據,一份來自嘉應學院網絡中心2017年5月—12月的訪問日志大數據,另一份是從各網絡平臺通過網絡爬蟲獲得,它們都是未經處理的語料大數據。

3.1.2 語料大數據處理及向量化

本文利用基于神經網絡的詞向量化工具連續詞袋模型(Continous Bag of Words Model,CBOW)[13]實現大數據語料處理,進行文本切割、清洗、分詞、詞性標注、去停用詞、詞向量化,將獨熱編碼的詞向量映射為分布形式的詞向量,從而降低維數和稀疏性,同時通過求向量間的歐氏距離或夾角余弦值得出任意詞間的關聯度[14]。具體處理過程如下:

1)首先遍歷數據集,將數字都用“0”替換,將http/、HTTP/、https/、HTTPS用“http://”替換;其次按照html標簽、JavaScript函數體、http://和參數規則進行分詞;接著基于日記文檔構建詞匯表,對單詞進行獨熱編碼。

2)構建基于神經網絡的詞向量化模型,包括輸入層、投射層和輸出層[15-16],其結構及訓練過程如圖2所示。然后輸入樣本,最小化損失函數并改變權值,訓練模型并獲得分布式詞向量。

3)統計正樣本詞集,用詞頻最高的3 000個詞構成詞庫,其他標記為“COM”。本文設定分布式特征向量的維數為128,當前詞與預測詞最大窗口距離為5,含64個噪聲詞,共進行5次迭代。

圖2 詞向量化CBOW模型及訓練過程Fig.2 Word vectorized CBOW model and training process

因為每條數據所占字符長度不同,所以本文以所占字符長度最大為標準,不足則以-1填充,在為數據集設計標簽時,使用獨熱編碼,正樣本標簽(即屬于攻擊樣本)以1表示,負樣本標簽(即正常網絡請求)以0表示。經過上述處理之后,共獲得正樣本數據集40 637條,負樣本數據集分別為105 912條和200 129條,它們數量大、計算復雜性高,均為大數據[17-19]。為提高訓練效果,將正樣本集和兩類負樣本集分別進行合并,隨機劃分為訓練集和測試集,數量比為7∶3,并記為第Ⅰ類大數據集和第Ⅱ類大數據集。

3.2 實驗檢測與結果

為驗證算法的有效性,設計多種DCNNs算法[20],構建基于“輸入層+卷積層+卷積層+池化層+卷積層+卷積層+池化層+全連接層+全連接層+Softmax層”10層深度的結構,并設計不同的超參數,包括樣本塊大小、學習率μ以及卷積層深度等[21-22],然后輸入大數據集詞向量樣本進行訓練和測試。為檢驗系統的穩定性,對每類數據分別進行20次實驗,結果及分析如下:

1)基于各深層DCNNs設計不同的超參數,學習率μ為0.001、0.01和0.1,對第 Ⅰ 類大數據集進行20次實驗得到的識別率結果如表1所示。

表1各深層DCNNs基于不同學習率對第Ⅰ類大數據集的>識別率結果

Table 1 Recognition rate results of each deep DCNNs for type Ibig dataset based on different learning rates

實驗次數識別率μ為0.001μ為0.01μ為0.110.981 40.993 40.831 320.991 20.994 20.830 830.992 00.994 20.831 040.992 80.994 50.830 950.993 50.994 80.830 560.993 60.994 90.830 570.994 00.995 10.830 680.994 00.994 90.830 390.994 30.995 30.830 1100.994 50.992 20.830 1110.994 50.994 90.830 0120.994 70.994 70.830 4130.995 00.994 80.830 7140.994 90.994 80.831 4150.994 70.994 90.829 8160.995 50.994 70.826 9170.995 80.994 80.829 4180.995 80.994 90.830 1190.995 30.995 00.829 7200.995 80.995 00.829 8

從表1可以看出,當學習率為0.001和0.01時,算法都有很高的識別率,其中,最低識別率為0.981 4,最高識別率為0.995 8,且識別率隨著訓練次數的增加一直保持較高水平并趨于穩定;而當學習率為0.1時,算法識別率稍低,平均為0.830 2左右,原因是學習率設置過大,導致訓練時梯度下降過快從而越過了最優值,相比而言,當學習率較小時能得到全局最優或接近最優。識別率的曲線圖表示如圖3所示。

圖3 基于不同學習率對第Ⅰ類大數據集進行20次實驗得到的識別率曲線

Fig.3 Recognition rate curve obtained from 20 experimentsfor type I big dataset based on different learning rates

2)基于不同的學習率,對第Ⅱ類大數據集進行20次實驗得到的識別率結果如表2所示。從表2可以看出,當學習率為0.001時,算法一直有穩定的高識別率,學習率為0.01時除了中間幾次稍低外其他都是高識別率,且識別率隨著訓練次數的增加總體上都保持增長狀態并趨于穩定;同樣當學習率為0.1時,識別率相對更低,平均為0.831 0左右。識別率的曲線圖表示如圖4所示。

表2各深層DCNNs基于不同學習率對第Ⅱ類大數據集的識別率結果

Table 2 Recognition rate results of each deep DCNNs for type IIbig dataset based on different learning rates

實驗次數識別率μ為0.001μ為0.01μ為0.110.980 80.983 30.830 820.996 70.994 80.830 930.997 30.993 60.831 440.997 60.985 70.830 950.997 70.975 30.831 060.997 90.988 30.831 070.998 10.989 10.831 180.998 20.989 20.830 990.998 40.989 40.831 1100.998 30.947 00.831 1110.998 50.836 20.830 8120.998 50.824 80.831 1130.998 70.806 80.831 3140.998 80.898 40.831 1150.998 70.924 90.831 2160.998 70.926 60.831 0170.998 80.926 70.830 9180.999 00.926 50.831 2190.998 80.927 30.831 1200.998 60.941 20.831 0

圖4 基于不同學習率對第Ⅱ類大數據集進行20次實驗得到的識別率曲線

Fig.4 Recognition rate curve obtained from 20 experiments fortype II big dataset based on different learning rates

3)基于各深層DCNNs設計不同的超參數,樣本塊大小(BatchSize)分別為50、100和500,對第 Ⅰ 類大數據集進行20次實驗得到的識別率結果如表3所示。從表3可以看出,BatchSize為100和500時算法都有很高的識別率,其中,最低識別率為0.988 6,最高識別率為0.995 5,且隨著訓練次數的增加都保持穩定的高識別率;當BatchSize為50時,識別率相對較低,平均為0.734 5。識別率的曲線圖表示如圖5所示。

表3各深層DCNNs基于不同BatchSize對第Ⅰ類大數據集的識別率結果

Table 3 Recognition rate results of each deep DCNNs for type Ibig dataset based on different BatchSizes

實驗次數識別率BatchSize為50BatchSize為100BatchSize為50010.951 10.988 60.993 420.748 90.991 60.994 230.721 70.992 10.994 240.721 70.992 60.994 550.721 70.993 10.994 860.721 70.993 40.994 970.721 70.993 90.995 180.721 70.993 90.994 990.721 70.994 20.995 3100.721 70.994 40.992 2110.721 70.994 60.994 9120.721 80.994 50.994 7130.721 70.994 60.994 8140.721 60.994 90.994 8150.721 70.995 10.994 9160.721 70.995 30.994 7170.721 70.995 00.994 8180.721 70.995 40.994 9190.721 70.995 20.995 0200.721 70.995 50.995 0

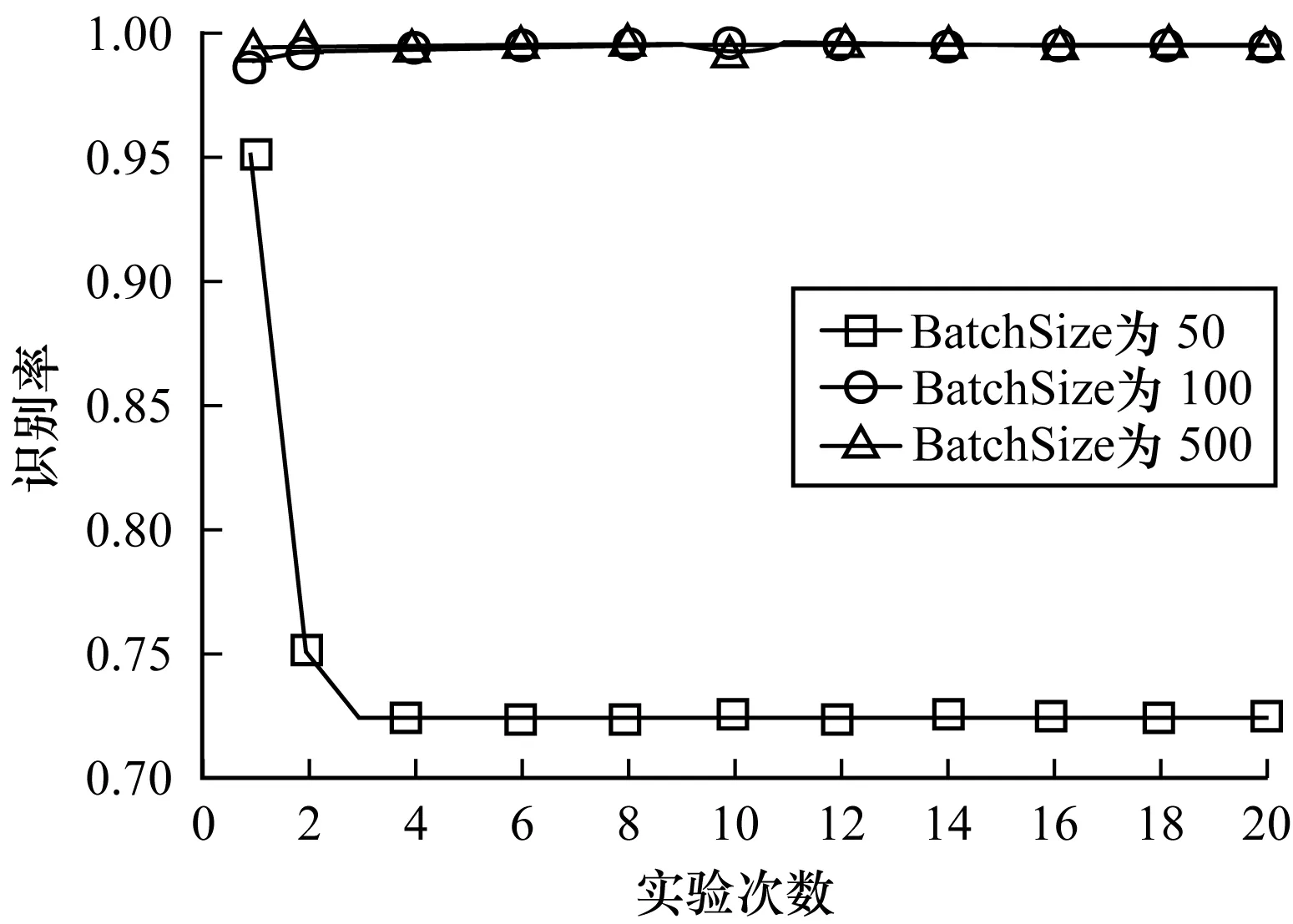
圖5 基于不同BatchSize對第Ⅰ類大數據集進行20次實驗得到的識別率曲線

Fig.5 Recognition rate curve obtained from 20 experiments fortype I big dataset based on different BatchSizes

4)基于不同的BatchSize,對第 Ⅱ 類大數據集進行20次實驗得到的識別率結果如表4所示。從表4可以看出,當BatchSize為500時算法有最好的平均識別率,其中,最低識別率為0.806 8,最高識別率為0.994 8;當BatchSize為50時,識別率稍有下降,平均值約為0.832 0;當BatchSize為100時,前6次識別率均接近0.912 1,之后下降幅度較大,僅為0.169 0左右。識別率的曲線圖表示如圖6所示。

表4各深層DCNNs基于不同BatchSize對第Ⅱ類大數據集的識別率結果

Table 4 Recognition rate results of each deep DCNNs for type IIbig dataset based on different BatchSizes

實驗次數識別率BatchSize為50BatchSize為100BatchSize為50010.850 80.908 80.983 320.830 90.917 80.994 830.831 40.912 10.993 640.830 90.909 50.985 750.831 00.909 50.975 360.831 00.899 90.988 370.831 10.168 90.989 180.830 90.169 10.989 290.831 10.168 90.989 4100.831 10.168 90.947 0110.830 80.169 20.836 2120.831 10.168 90.824 8130.831 30.168 70.806 8140.831 10.168 90.898 4150.831 20.168 80.924 9160.831 00.169 00.926 6170.830 90.169 10.926 7180.831 20.168 80.926 6190.831 10.168 90.927 3200.831 00.169 00.941 2

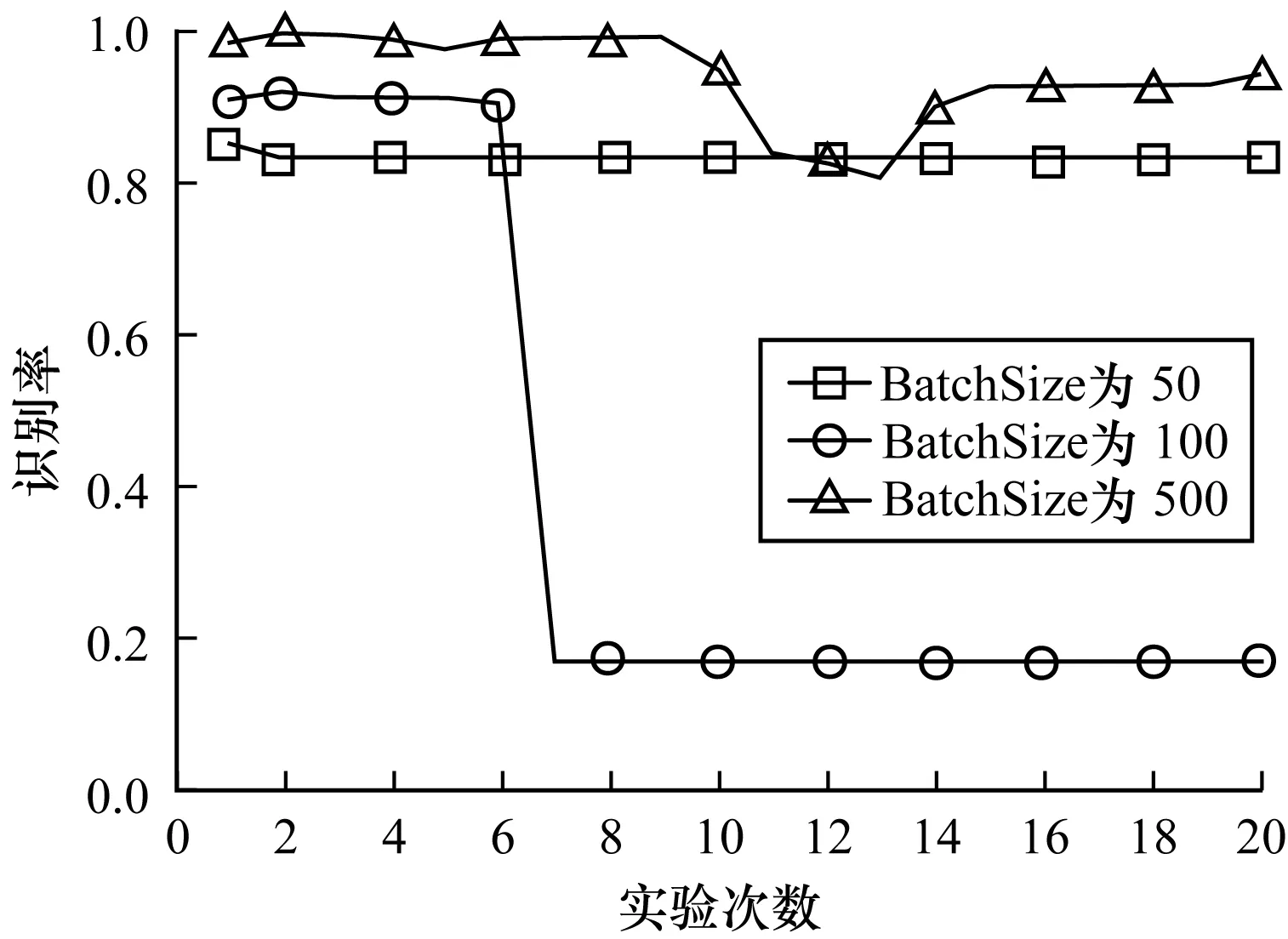
圖6 基于不同BatchSize對第Ⅱ類大數據集進行20次實驗得到的識別率曲線

Fig.6 Recognition rate curve obtained from 20 experimentsfor type II big dataset based on different BatchSizes

5)為進一步驗證系統的相關特性,基于各深層DCNNs設計不同的卷積層深度,對第Ⅰ類大數據集進行20次實驗得到的識別率結果如表5所示。從表5可以看出,算法總體都保持高識別狀態,其中,最低識別率為0.976 0,最高識別率為0.993 0。識別率的曲線圖表示如圖7所示。

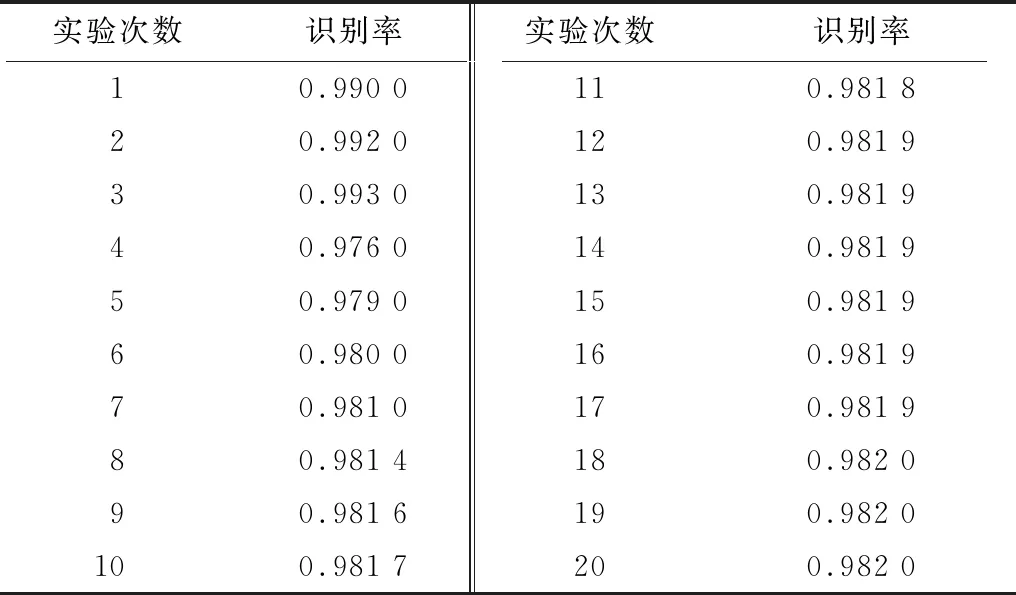
表5 深層DCNNs對第Ⅰ類大數據集的識別率結果Table 5 Recognition rate results of deep DCNNs on type Ibig dataset

圖7 DCNNs對第Ⅰ類大數據集進行20次實驗得到的識別率曲線

Fig.7 Recognition rate curve obtained from 20 experimentsof DCNNs for type I big dataset

6)基于不同的卷積層深度,對第 Ⅱ 類大數據集進行20次實驗得到的識別率結果如表6所示。從表6可以看出,隨著訓練的進行,算法識別率不斷提高,其中,最低識別率為0.980 8,最高識別率為0.999 0,最后趨于穩定。識別率的曲線圖表示如圖8所示。

表6 深層DCNNs對第Ⅱ類大數據集的識別率結果Table 6 Recognition rate results of deep DCNNs for type IIbig dataset

圖8 DCNNs對第Ⅱ類大數據集進行20次實驗得到的識別率曲線

Fig.8 Recognition rate curve obtained from 20 experimentsof DCNNs for type II big dataset

通過實驗可以看出,各深層DCNNs基于不同學習率μ對第 Ⅰ 類大數據集的平均識別率為99.366 5%,方差為0.000 001,標準差為0.000 944,如表7所示。各深層DCNNs基于不同學習率μ對第Ⅱ類大數據集的平均識別率為93.875 5%,方差為0.000 015,標準差為0.003 952,如表8所示。通過實驗也可以看出,各深層DCNNs基于不同BatchSize對第 Ⅰ 類大數據集的平均識別率為99.389 5%,方差為0.000 003,標準差為0.001 670,如表9所示。各深層DCNNs基于不同BatchSize對第Ⅱ類大數據集的平均識別率為83.204 5%,方差為0.003 258,標準差為0.058 559,如表10所示。另外,通過實驗可以得到,各深層DCNNs基于不同卷積層深度對第 Ⅰ 類大數據集的平均識別率為98.274 5%,方差為0.000 016,標準差為0.004 133,如表11所示。各深層DCNNs基于不同卷積層深度對第Ⅱ類大數據集的平均識別率為99.740 5%,方差為0.000 015,標準差為0.003 952,如表12所示。

表7各深層DCNNs基于不同學習率對第Ⅰ類大數據集的平均識別率、方差和標準差

Table 7 Average recognition rate,variance and standarddeviation of each deep DCNNs for type I big datasetbased on different learning rates

學習率平均識別率/%方差標準差0.00199.366 50.000 0090.003 1390.01099.460 00.000 0000.000 6970.10083.021 50.000 0010.000 944

表8各深層DCNNs基于不同學習率對第Ⅱ類大數據集的平均識別率、方差和標準差

Table 8 Average recognition rate,variance and standarddeviation of each deep DCNNs for type II big datasetbased on different learning rates

學習率平均識別率/%方差標準差0.00199.740 50.000 0150.003 9520.01093.875 50.003 2580.058 5600.10083.104 50.000 0000.000 157

表9各深層DCNNs基于不同BatchSize對第Ⅰ類大數據集的平均識別率、方差和標準差

Table 9 Average recognition rate,variance and standarddeviation of each deep DCNNs for type I big datasetbased on different BatchSizes

BatchSize平均識別率/%方差標準差5073.453 00.002 5040.051 33610099.389 50.000 0030.001 67050099.460 00.000 0000.000 697

表10各深層DCNNs基于不同BatchSize對第Ⅱ類大數據集的平均識別率、方差和標準差

Table 10 Average recognition rate,variance and standarddeviation of each deep DCNNs for type II big datasetbased on different BatchSizes

BatchSize平均識別率/%方差標準差5083.204 50.000 0190.004 41710039.113 50.115 2110.348 24550093.876 00.003 2580.058 559

表11深層DCNNs對第Ⅰ類大數據集的平均識別率、方差和標準差

Table 11 Average recognition rate,variance and standarddeviation of deep DCNNs for type I big dataset

卷積深度平均識別率/%方差標準差1098.274 50.000 0160.004 133

表12深層DCNNs對第Ⅱ類大數據集的平均識別率、方差和標準差

Table 12 Average recognition rate,variance and standarddeviation of deep DCNNs for type II big dataset

卷積深度平均識別率/%方差標準差1099.740 50.000 0150.003 952

對于第 Ⅰ 類和第 Ⅱ 類大數據集,基于不同學習率μ的識別率均值如圖9所示,標準差均值如圖10所示。對于第 Ⅰ 類和第 Ⅱ 類大數據集,基于不同BatchSize的識別率均值如圖11所示,標準差均值如圖12所示。

圖9 基于不同學習率對第Ⅰ類和第Ⅱ類大數據集的識別率均值

Fig.9 Average recognition rate for type I and type II bigdatasets based on different learning rates

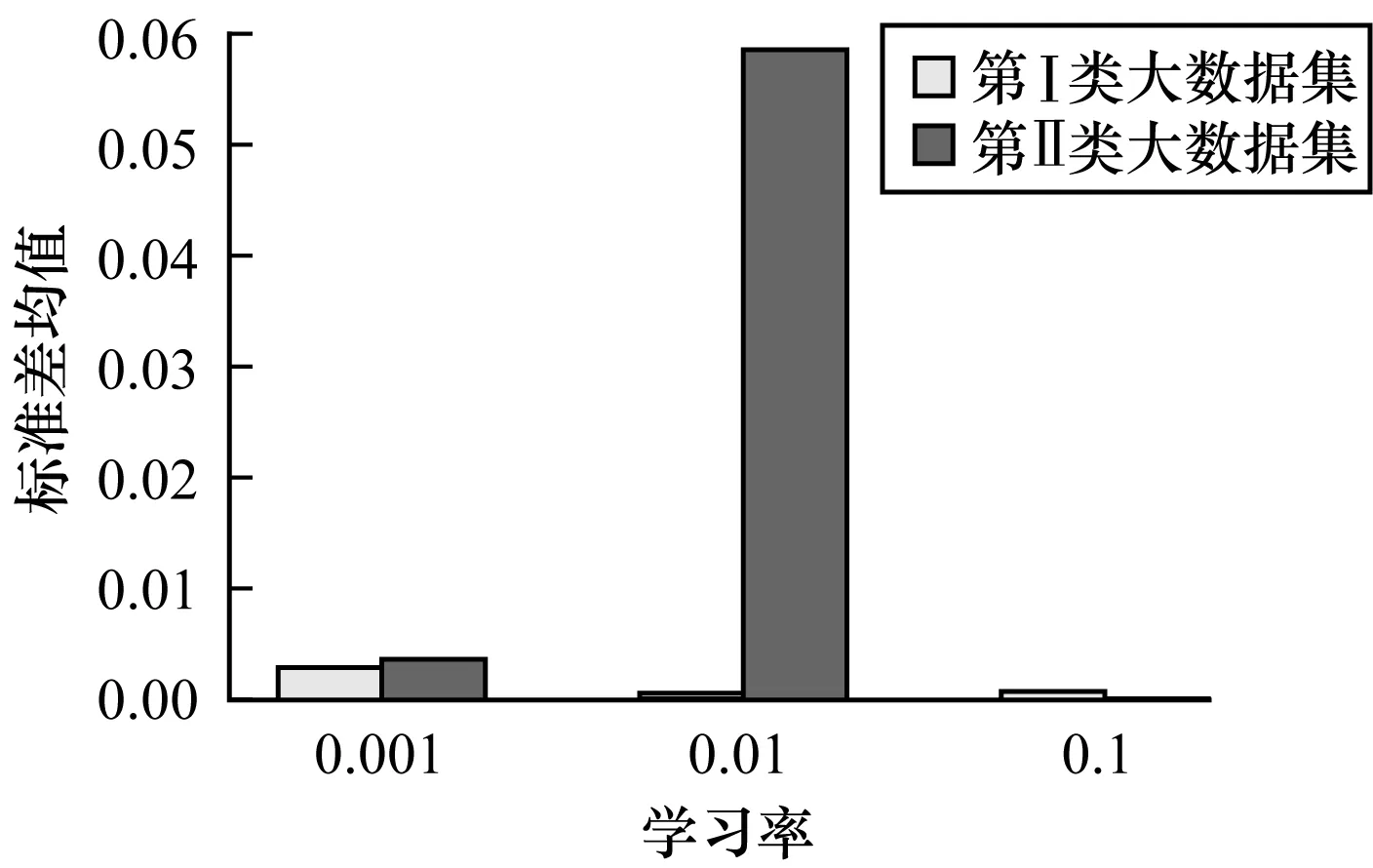
圖10 基于不同學習率對第Ⅰ類和第Ⅱ類大數據集的標準差均值

Fig.10 Mean standard deviation for type I and type IIbig datasets based on different learning rates

圖11 基于不同BatchSize對第Ⅰ類和第Ⅱ類大數據集的識別率均值

Fig.11 Average recognition rate for type I and type II bigdatasets based on different BatchSizes

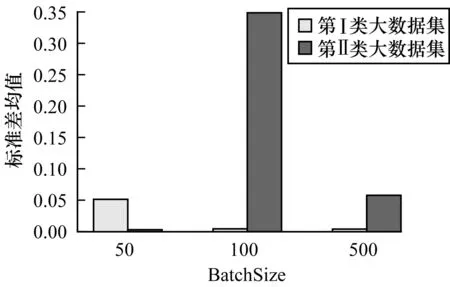
圖12 基于不同BatchSize對第Ⅰ類和第Ⅱ類大數據集的標準差均值

Fig.12 Mean standard deviation for type I and type II big

datasets based on different BatchSizes

系統識別率變化過程曲線圖如圖13所示,可以看出,識別率隨著訓練的進行逐漸提高,隨后降低然后又不斷提高并趨于穩定,總體識別率較高。損失函數誤差變化曲線圖如圖14所示,可以看出,隨著訓練的進行,損失函數誤差先減少后增加然后不斷地減小并趨于穩定,其與識別率的變化過程相一致。詞向量樣本余弦距離變化曲線圖如圖15所示,可以看出,隨著訓練的進行,余弦距離先減小后增加然后不斷地減小并趨于穩定,這反映了詞向量樣本的相關性先增強后變小然后越來越強,其同識別率變化過程也一致。平均絕對誤差變化過程曲線圖如圖16所示,可以看出,隨著訓練的進行,平均絕對誤差先減小后增加然后不斷地減小并趨于最小的穩定值。

圖13 識別率變化曲線Fig.13 Curve of recognition rate change

圖14 損失函數誤差變化曲線Fig.14 Curve of loss function error change

圖15 余弦距離變化曲線Fig.15 Curve of cosine distance change

圖16 平均絕對誤差變化曲線Fig.16 Curve of average absolute error change

4 結束語

傳統的計算機病毒檢測方法主要依據病毒特征庫中的已有特征，通過特征匹配來確定病毒是否存在，其難以檢測新出現的病毒以及變形病毒，而且檢測效率較低。為解決該問題，本文通過類圖像處理及向量化方法對訪問流量語料庫大數據進行詞向量化處理，從而實現了面向大數據跨站腳本攻擊的智能檢測。實驗結果表明，該方法具有識別率高、穩定性好、總體性能優良等優點。下一步將探討小樣本數據的智能檢測問題,以更全面地進行入侵智能檢測。