輸電導(dǎo)線覆冰舞動(dòng)動(dòng)力特性研究

鄧友晶，陳永宏

（中國(guó)電建集團(tuán)湖北工程有限公司，湖北 武漢 430040）

2018年初，湖北地區(qū)輸電線路發(fā)生大規(guī)模舞動(dòng)受災(zāi)，多條線路出現(xiàn)因舞動(dòng)導(dǎo)致的桿塔損壞情況。輸電導(dǎo)線舞動(dòng)現(xiàn)象，多發(fā)生于開(kāi)闊地帶。對(duì)于輸電線路而言，大截面、多分裂導(dǎo)線較于大截面、單分裂導(dǎo)線更易舞動(dòng)[1-3]。舞動(dòng)發(fā)生時(shí)，全檔架空線路會(huì)發(fā)生大幅度波浪式振動(dòng)。長(zhǎng)時(shí)間大幅度的舞動(dòng)容易引起金具損壞、相間閃絡(luò)，導(dǎo)致倒塔或者線路跳閘等重大事故，從而造成重大經(jīng)濟(jì)損失。

1 舞動(dòng)機(jī)理介紹

影響舞動(dòng)的主要因素包括覆冰、風(fēng)和線路結(jié)構(gòu)[4]。

輸電導(dǎo)線舞動(dòng)的數(shù)學(xué)模型，通常可分為如下3種[5]。

（1）單自由模型。這是一種與Den Hartog垂直舞動(dòng)機(jī)理相對(duì)應(yīng)的模型，通常只考慮輸電導(dǎo)線的豎向振動(dòng)。

（2）二自由模型（包括兩種），一是考慮輸電線路的豎向振動(dòng)和水平擺動(dòng)二者相互耦合的情況，二是基于O.Nigol扭轉(zhuǎn)舞動(dòng)機(jī)理，考慮豎向振動(dòng)和軸向扭轉(zhuǎn)相互耦合。

（3）三自由度模型。這種模型通常需考慮垂向振動(dòng)、水平擺動(dòng)和軸向扭轉(zhuǎn)三者相互耦合的情況。

2 導(dǎo)線舞動(dòng)動(dòng)力特性

本文基于O.Nigol扭轉(zhuǎn)舞動(dòng)理論。O.Nigol扭轉(zhuǎn)舞動(dòng)理論一方面考慮了導(dǎo)線自己扭轉(zhuǎn)影響，另一方面考慮了在風(fēng)激勵(lì)條件下偏心覆冰導(dǎo)線的空氣動(dòng)力特性。O.Nigol理論認(rèn)為舞動(dòng)主要是導(dǎo)線自激扭轉(zhuǎn)而引起的。

導(dǎo)線系統(tǒng)的失穩(wěn)條件為：

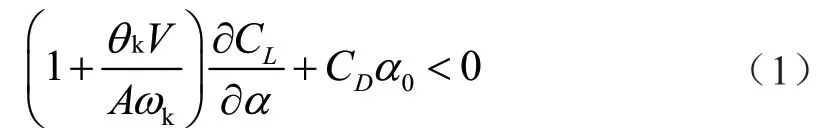
其中，CL、CD分別為導(dǎo)線氣動(dòng)升力系數(shù)，θk、ωk分別為導(dǎo)線第k階扭轉(zhuǎn)振動(dòng)的波腹振幅、角頻率；V為與線路走向垂直的水平風(fēng)速；α0為偏心覆冰導(dǎo)線初迎風(fēng)攻角。

當(dāng)導(dǎo)線向上運(yùn)動(dòng)，速度為v，可以等同于水平風(fēng)速V同時(shí)有一個(gè)向下的速度v。此時(shí)相對(duì)速度為Vr，等同于風(fēng)從左上方吹向橢圓長(zhǎng)軸位于水平的導(dǎo)線，水平風(fēng)向與相對(duì)風(fēng)向的夾角Δθ為：

其中，V為相對(duì)風(fēng)速的水平值，v為相對(duì)風(fēng)速的垂直值。

3 覆冰導(dǎo)線的舞動(dòng)計(jì)算

關(guān)于輸電導(dǎo)線舞動(dòng)計(jì)算的核心內(nèi)容即為計(jì)算風(fēng)荷載作用下對(duì)覆冰導(dǎo)線所產(chǎn)生的空氣動(dòng)力載荷。根據(jù)覆冰導(dǎo)線的空氣動(dòng)力學(xué)公式，F(xiàn)L升力、FD阻力和FM扭矩的計(jì)算公式如下：

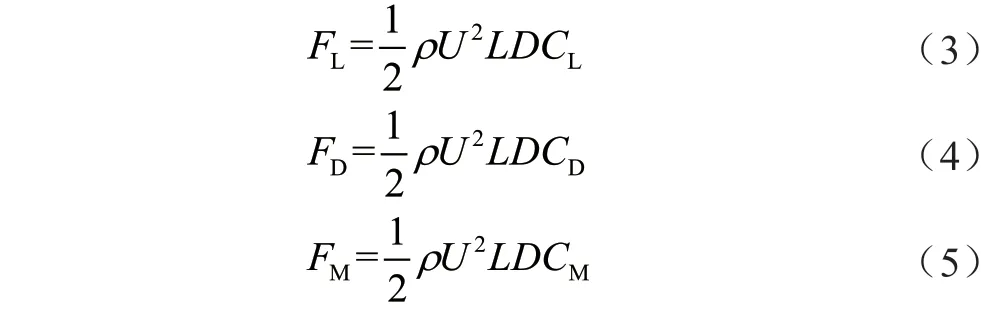
其中，F(xiàn)L為單位長(zhǎng)度的導(dǎo)線模型升力，F(xiàn)D是單位長(zhǎng)度的導(dǎo)線模型單位阻力，F(xiàn)M為扭矩。ρ為流體密度，U為前方來(lái)流均勻速度，L為導(dǎo)線長(zhǎng)度，D為導(dǎo)線直徑。

4 響應(yīng)面分析

通過(guò)有限元Fluent軟件建立新月形覆冰單導(dǎo)線模型，基于響應(yīng)面分析方法，通過(guò)Matlab軟件對(duì)數(shù)據(jù)進(jìn)行擬合處理，分析得到不同覆冰厚度，不同風(fēng)速條件下，對(duì)應(yīng)的覆冰導(dǎo)線阻力系數(shù)、升力系數(shù)和扭矩系數(shù)。

覆冰厚度取為7.5 mm時(shí)，不同風(fēng)速和風(fēng)攻角對(duì)應(yīng)的阻力系數(shù)CD、升力系數(shù)CL和扭矩系數(shù)CM響應(yīng)面分別如圖1、圖2和圖3所示。

圖1 阻力系數(shù)CD

圖2 升力系數(shù)CL

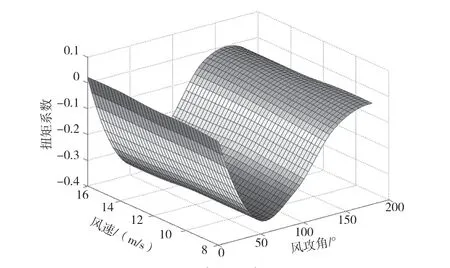
圖3 扭矩系數(shù)CM

風(fēng)速取為10 m/s時(shí)，不同風(fēng)速和風(fēng)攻角對(duì)應(yīng)的阻力系數(shù)CD、升力系數(shù)CL和扭矩系數(shù)CM響應(yīng)面分別如圖4、圖5和圖6所示。

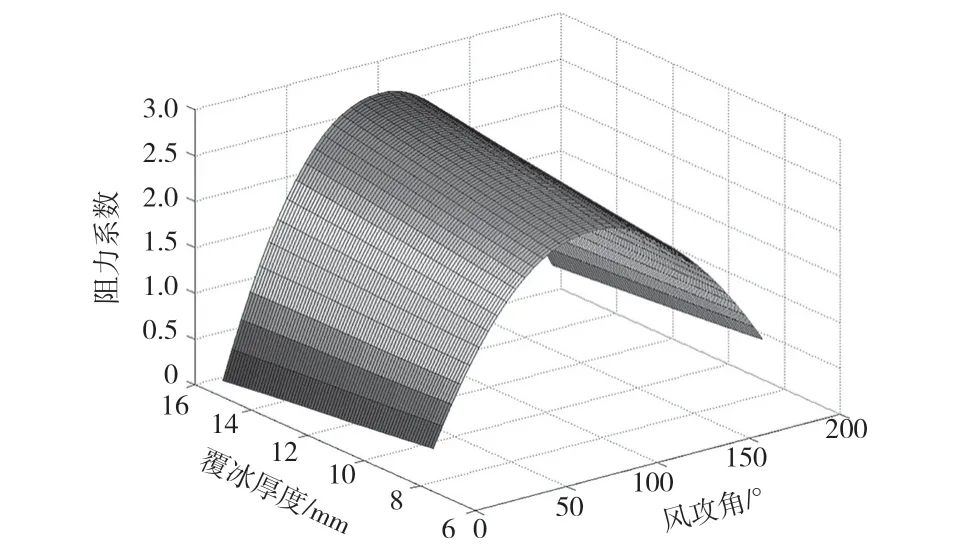
圖4 阻力系數(shù)CD

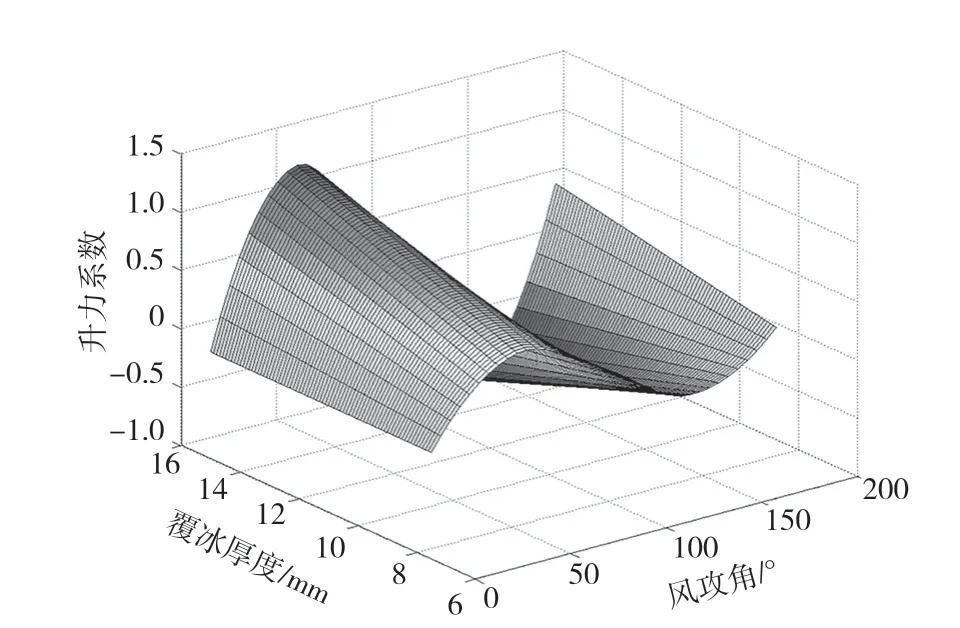
圖5 升力系數(shù)CL

圖6 扭矩系數(shù)CM

風(fēng)攻角取為45°時(shí)，不同風(fēng)速和風(fēng)攻角對(duì)應(yīng)的阻力系數(shù)CD、升力系數(shù)CL和扭矩系數(shù)CM響應(yīng)面分別如圖7、圖8和圖9所示。

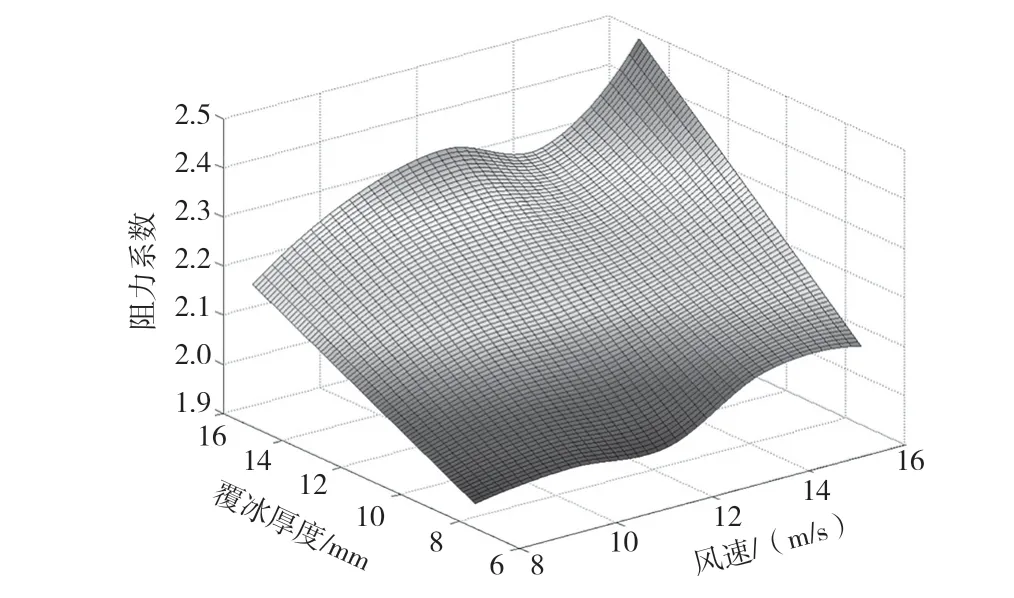
圖7 阻力系數(shù)CD

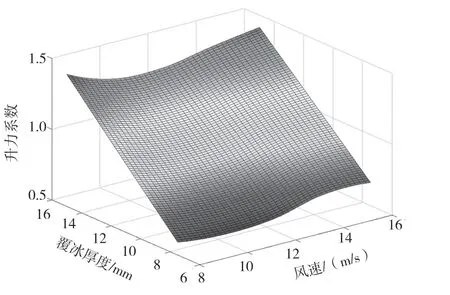
圖8 升力系數(shù)CL

圖9 扭矩系數(shù)CM

5 結(jié) 論

（1）O.Nigol扭轉(zhuǎn)舞動(dòng)機(jī)理適用于一般輸電線路工程導(dǎo)線的覆冰舞動(dòng)研究。

（2）導(dǎo)線舞動(dòng)的形成因素主要取決于覆冰厚度、風(fēng)速及風(fēng)攻角大小，不同的覆冰厚度、風(fēng)速和風(fēng)攻角對(duì)覆冰導(dǎo)線舞動(dòng)具有不同的影響。

（3）根據(jù)響應(yīng)面分析結(jié)果可知，氣動(dòng)阻力系數(shù)在攻角90°左右到達(dá)最大值，并且關(guān)于180°攻角對(duì)稱(chēng)；氣動(dòng)升力系數(shù)在攻角45°左右達(dá)到最大值，在攻角大于90°后，氣動(dòng)升力變?yōu)樨?fù)值；氣動(dòng)扭矩系數(shù)在攻角60°左右達(dá)到最小值。