關注高中數學重疊內容,以問題驅動式實施高等數學教學
郭從洲 張冬燕 王耀革 田園


【摘要】高中數學與高等數學部分內容的重疊與脫節,使得大一學生對高等數學的教學內容和重要性產生誤解.本文堅持“以學生為中心”的教學理念,以導數的概念教學內容為例題,設計一種問題驅動式的教學模式,在復習高中數學知識的同時,引入高等數學中的同類概念,提升學生對高等數學知識的認識高度.
【關鍵詞】高中數學;高等數學;問題驅動式
我國幾十年來的教學改革,不論采用什么樣的教學手段和什么樣的教學方法,最大的變化就是把“以教師為中心”的課堂轉變為“以學生為中心”的課堂.這種轉變看似簡單,實際操作起來卻非常困難.“以學生為中心”的課堂轉變不僅僅在高中數學教學中需要思考與改革,在大學數學課堂教學中同樣需要思考與改革.
1 高中數學與高等數學內容銜接中存在的問題
在我國新一輪的中學課程改革背景下,高中數學一直將導數、極值、定積分等作為選擇性必修內容,并且將這些內容列入了高考考試范圍.這不僅有利于與國際中學數學接軌,也有利于學生進入大學以后迅速地投入高等數學內容的學習.高中數學中關于微積分的內容是基于高中生年齡階段可以認知的能力范圍內撰寫的,其中缺乏嚴密的數學極限概念,缺少微積分的基本分析.當然,這基本符合微積分創立和完善的史實,也符合人們正常的認知規律.如果大學的高等數學老師不能夠充分認識高中數學關于微積分部分內容學習的上述目的和編寫原則,不能夠在開課伊始給學生講解清楚高等數學中函數、極限和連續的分析基礎的重要性,那么很容易給大學新生造成一種假象——高等數學僅僅是高中數學的簡單重復和個別延伸,課下自學就可以達到考試基本要求.殊不知,高等數學是微積分發展歷史的倒敘,是一種完備的、嚴密的數學知識,更是學生第一次使用嚴謹、簡潔、明晰的數學語言描述自然世界.
很多學生認為,高中學過的知識要略講,簡單介紹一下背景就可以,而高中沒學過的知識要詳細講解.表面上看這是高等數學與初等數學銜接的問題,而實質上是學生每天都希望老師講授新穎的、沒見過的知識.為了面對高考,很多學校在高中二年級上學期就已經把高中數學所有的內容講解完畢,利用一年半甚至更多的時間進行復習和刷題,學生經過漫長的磨煉進入大學,更渴望學習的是新知識、新內容.在課堂教學和作業批改中,經常發現學生不愿意使用高等數學中介紹的簡便的、高等的方法解題,更愿意使用初等的方法,很多解題的思路還停留在高中階段.比如,判斷函數在某一點是否存在極值的問題上,學生大都喜歡使用第一充分條件,不愿意使用第二充分條件.
堅持“以學生為中心”的教學改革理念,就是要教師充分了解學生的知識背景和學習過程,在教學過程中對舊的知識簡單復習,對新的內容詳細講解,使學生在每節課的學習中都有新的收獲和感受,激發學生學習高等數學的欲望和潛能.
2 針對重疊內容的問題驅動教學模式設計
高中數學與高等數學內容重疊既有有利的一面,又有不利的一面.作為大學數學老師,要通過各種教學模式的引入,想方設法將不利的一面化為有利的一面,努力為國家培養合格的人才.本文以我國絕大部分高中數學選修系列2-2(人民教育出版社A版教材)與高等數學(同濟大學編著教材)重疊的教學內容之一——導數為例,設計一種以學生為中心的問題驅動式教學模式,希望能夠總結出提升學生學習能力的教學經驗.
2.1 高中數學關于導數定義的講解過程
高中數學是通過兩個具體例子引入導數定義的:一是氣球膨脹率——氣球半徑增加的速率,二是高臺跳水——運動員下降的速率,通過分析、對比歸納出一個關于平均變化率的數學式子:f(x2)-f(x1)x2-x1.然后開始做大量的練習題,計算函數的平均變化率,鞏固學生對平均變化率的記憶,使得后面在講解曲線割線斜率的概念時也比較容易些.當學生熟悉了平均變化率以后,教材中有這樣一段話:“從物理角度看(瞬時速度),當時間間隔無限變小時,平均速度v-就無限趨近于瞬時速度,為了表述方便,我們用limΔt→0h(2+Δt)-h(2)Δt=-13.1表示“當t=2,Δt趨近于0時,平均速度v-趨近于確定值-13.1.”這是學生第一次接觸到極限的概念和符號,雖然只是一個描述性的定義.最后給出導數的定義是這樣描述的:
2.2 高等數學關于導數定義的講解過程
高等數學也是通過兩個具體例子引入導數定義的,一個是平面曲線在固定點處切線的斜率,另一個是物體沿直線運動的瞬時速度.通過對這兩個問題的分析、歸納抽象出一個特殊的極限式子:
2.3 高中數學與高等數學關于導數定義的異同
高中數學與高等數學關于導數定義的相同點有三個方面:一是在講解過程中都是通過兩個具體的問題引入的,二是對例題的分析過程中都是通過觀察、分析、歸納的合情推理方式總結出數學規律的,三是都抽象形成了一個利用極限表述的數學公式.從問題的引入到概念的形成基本都是一致的.
高中數學與高等數學關于導數定義內容講解的不同點主要表現在導數定義的描述上.高中數學由于沒有學習精確的極限定義,所以通過物理意義和幾何直觀,用描述性的極限定義給出了導數的概念,是一種定性化的概念;高等數學在學習過精確極限定義的基礎上,很自然地把一個特殊代數分式的極限命名為導數,是一種定量化的概念.可見,高中數學是在高中生的認知能力上定性化地定義了導數,而高等數學是在大學新生學習了精確極限概念的基礎上定量化地定義了導數.
2.4 問題驅動式的教學模式設計
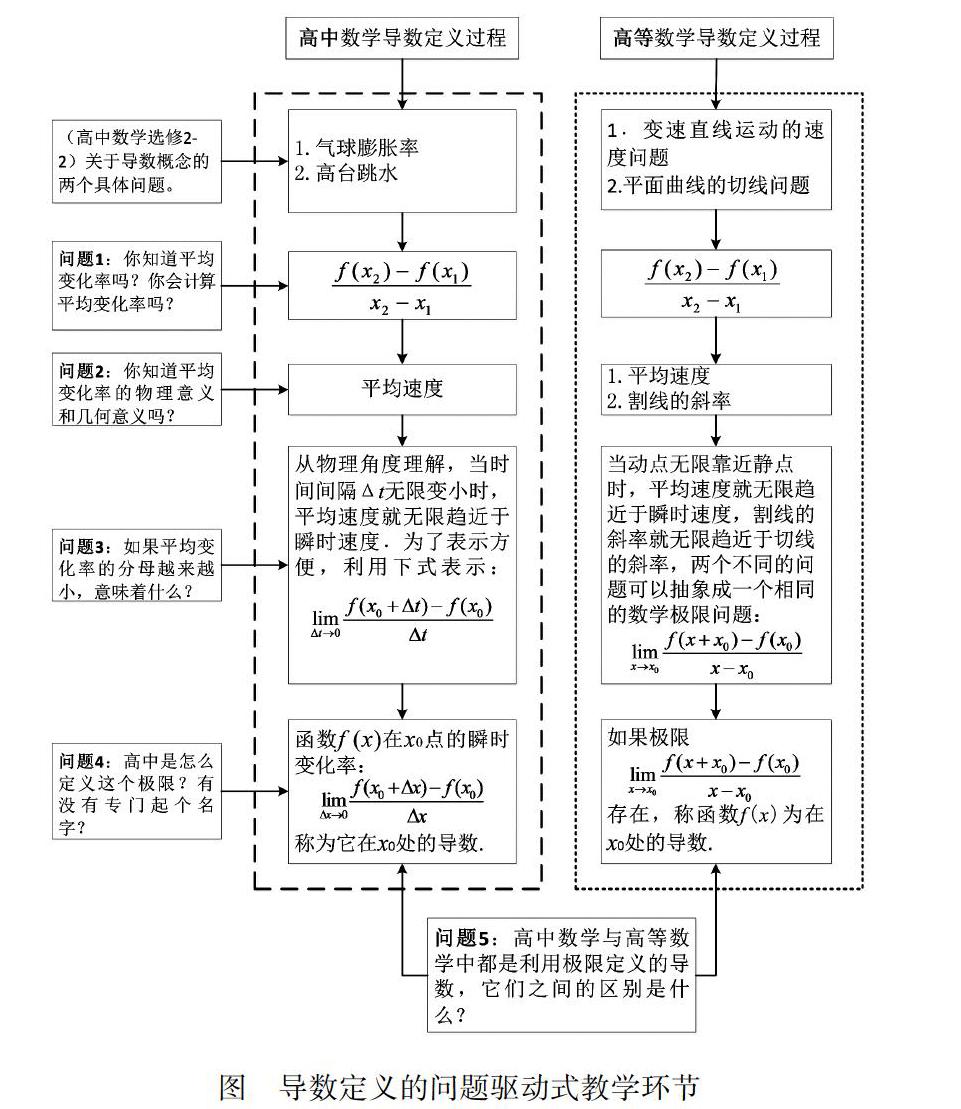
堅持“以學生為中心”的教學理念,教學過程就不能忽視學生以前的學習基礎.基于學生高中學習過導數的概念,我們認為采用問題驅動式的教學模式比較適合本節內容教學.首先,教師需要在教學過程中通過設置不同的問題讓學生回憶高中知識,引出高中極限概念,其次,設置不同的問題引導學生復習高等數學中學到的精確極限定義,重新審視高中關于導數的定義,進而引出導數的精確極限定義概念,再次,通過精確極限定義形式,引出導數存在的必要條件和充要條件,最后,總結高中數學和高等數學關于導數概念的異同點.主要教學環節和流程如下:
3 結束語
高中數學與高等數學的銜接問題,除了內容的銜接以外,還涉及學習方法、學習態度、學習目標、學習動力等部分的銜接.這些銜接問題的解決更需要堅持“以學生為中心”的教學理念,在教學過程中逐漸滲透講解.從教學模式、考核方式、問題引入和歷史回顧等方面深入改革,培養新時代大學生自我學習、終生學習的正確學習觀.
【參考文獻】
[1]同濟大學數學系.高等數學:第七版[M].北京:高等教育出版社,2017.
[2]中學數學課程教材研究開發中心.高中數學選修2-2[M].北京:人民教育出版社,2015.
[3]趙富. 淺析初等數學與高等數學的銜接與發展[J]. 黑龍江科學, 2016(13):84-85.
[4]汪小梅, 朱華, 楊志鵬. 淺談高等數學與初等數學的銜接問題[J]. 科教導刊:電子版, 2016(10):102-103.
[5]南曉雪. 初等數學與高等數學教學銜接問題的研究[J]. 當代教育實踐與教學研究, 2017(02):176.
6. 李紅霞. 初等數學與高等數學學習方法的銜接現狀及措施[J]. 數學學習與研究:教研版, 2010(1):3-3.

