CFRP三維銑削仿真模型的建立及層間損傷分析

秦旭達 唐心凱 葛恩德 李士鵬 朱圣富

（1 天津大學機械工程學院，天津 300072）

（2 上海飛機制造有限公司航空制造技術研究所，上海 201324）

0 引言

碳纖維增強樹脂基復合材料（CFRP）具有比強度和比模量高、抗腐蝕性和耐疲勞性好等諸多優點，在航空航天領域應用廣泛［1］。雖然大多數復合材料采用近凈成形加工，但通常為了滿足零件尺寸及裝配要求等，需要對復合材料零件進行銑削加工［2］。但CFRP 是一種典型的難加工材料，在加工過程中易產生層間損傷，嚴重影響加工質量以及工件的使用壽命［3］。因此，研究CFRP 層間損傷產生機理進而減少加工損傷是當前亟需解決的問題。

由于復合材料試件和刀具價格昂貴以及層間損傷不易檢測，僅通過實驗方法對加工損傷產生機理進行研究需要很高的實驗成本。因此有限元仿真與實驗相結合的方式逐漸成為一種較優的分析方法。針對復合材料切削的有限元仿真，大部分國內外學者［4-7］關注二維切削仿真，但二維切削模型無法分析面外失效以及刀具的某些具體角度（螺旋角等）對切削過程的影響，三維切削仿真結果更接近實際，已逐漸成為CFRP 仿真建模的關注重點。CFRP 三維建模需要自定義CFRP 的力學模型，相應理論還未成熟，部分學者已經開始對復合材料三維切削有限元仿真展開研究，例如，A. Vaibhav 等人［8］建立了復合材料三維鉆削有限元模型，用Cohesive單元模擬復合材料中的層間分層，分析了鉆孔工藝參數對分層損傷的影響。賈振元等人［9］開發了CFRP/Ti 疊層材料三維斜角切削模型，探究了切削不同纖維方向與不同鋪層順序時面下損傷的變化。宿友亮［10］建立了CFRP的三維正交切削有限元模型，利用該模型對微切削過程進行了仿真，對纖維和樹脂的斷裂演化過程進行了表征。A.Abena 等人［11］利用光滑粒子流體動力學與有限元相結合的方法建立了CFRP 細觀三維正交切削模型，仿真精度較好。齊振超［12］建立了三維鉆削CFRP 有限元模型，直觀表現了分層產生過程和應力場分布規律。綜上可知，對于復合材料三維有限元建模的層間損傷研究，三維正交切削模型與鉆削模型占絕大多數，且模型中大多未考慮CFRP 的剛度退化部分。以往的研究中還沒有銑削加工中纖維方向角對層間損傷的影響規律研究。

本文基于ABAQUS 有限元仿真技術，建立可預測層間損傷和剛度退化的CFRP 三維銑削有限元模型，分析了切削力、層間應力、層間損傷隨纖維方向角的變化規律，對于銑削刀具和工藝優化具有一定的技術參考價值。

1 CFRP三維銑削有限元模型

1.1 CFRP層合板損傷演化理論

建立三維銑削模型為宏觀模型，單層板設置為等效均質的模型，不區分纖維與基體［13-14］。通過自定義子程序（VUMAT）的開發，構建出三維線彈性本構、三維失效準則及損傷演化在內的復合材料模型，復合材料板層與層之間通過Cohesive單元連接，以模擬層間損傷。

1.1.1 層內損傷演化理論

CFRP 損傷起始判據采用Hashin 失效準則［15-16］，Hashin準則包含四種不同的失效形式。

纖維拉伸失效（σ11≥0）：

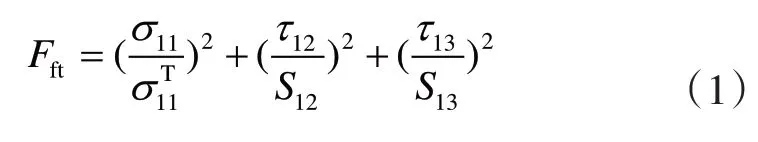
纖維壓縮失效（σ11＜0）：

垂直于纖維方向拉伸失效（σ22+σ33≥0）：

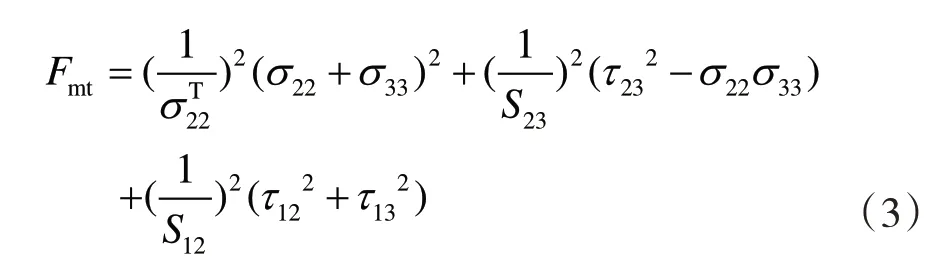
垂直于纖維方向壓縮失效（σ22+σ33＜0）：

式中，Fft、Ffc、Fmt、Fmc分別是四種失效模式的損傷變量；σ11、σ22、σ33、τ12、τ13、τ23是單元積分點處應力張量的分量分別是纖維方向的拉伸、壓縮破壞應力，垂直于纖維方向的拉伸、壓縮破壞應力；S12、S13、S23分別是1-2 平面、1-3 平面、2-3 平面的剪切破壞應力。

一旦積分點達到損傷起始條件，該點就會進行剛度退化，剛度退化通過剛度退化系數進行控制，而剛度退化系數的演化規律尚未有統一的形式，其中指數損傷演化規律已經被證明是有效的，具有良好的收斂性［17］。由于Hashin 準則包含四種失效條件，與之對應有四種損傷因子di。

纖維拉伸失效（σ11≥0）：

纖維壓縮失效（σ11＜0）：

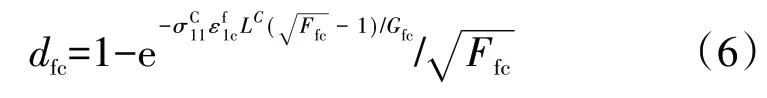
垂直于纖維方向拉伸失效（σ22+σ33≥0）：

垂直于纖維方向壓縮失效（σ22+σ33＜0）：

式中，LC為單元的特征長度，Gft、Gfc、Gmt、Gmc為纖維拉伸、纖維壓縮、基體拉伸、基體壓縮的斷裂能為單元積分點處應變張量的分量。

損傷因子di控制著剛度退化，如公式（9）所示［17］，即當滿足起始失效準則后，損傷產生并累積，損傷因子從0 開始增加，當達到1 時，剛度退化為最小值。當dft達到1 時，即沿纖維方向拉伸完全失效，單元被刪除。

1.1.2 層間損傷演化理論

層間通過Cohesive 單元連接并傳遞應力，Cohesive 單元應力應變相應如圖1 所示，在切削載荷作用下，Cohesive 單元發生線彈性變形，達到臨界等效應力后產生損傷發生剛度退化，最終單元刪除，層間開裂。

圖1 Cohesive單元應力應變關系Fig.1 Stress-strain of cohesive elements

采用二次名義應力準則作為層間單元損傷起始判據，此準則用公式（10）表示。當各方向的名義應力比的平方和達到1時，損傷產生。

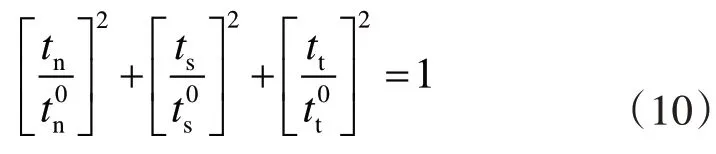
式中，tn、ts、tt為界面法向和剪切方向的瞬時應力、為界面法向和剪切方向的最大名義應力。

關于Cohesive單元的損傷演化，基于能量的損傷演化規律得到廣泛應用，采用基于斷裂能的Powerlow判據確定斷裂能在混合模式下的關系如下：

式中，Gn、Gs、Gt為界面法向及剪切方向的瞬時斷裂能為法向及剪切方向破壞所需的臨界斷裂能，指數常數β為1.6［18］。

仿真中使用的Cohesive 單元的性能參數見表1［18］。

表1 Cohesive單元性能參數1）Tab.1 Property parameters for Cohesive element

1.2 有限元模型設置

三維銑削CFRP 有限元模型主要由三大部分組成：刀具、層合板、層間部分，由于尺寸及層數的增加會導致計算效率急劇降低，而層間應力及損傷主要集中在切削區，故將模型簡化為如圖2 所示，工件的尺寸為5 mm×3 mm×2 mm，分為4 層，每層厚0.5 mm；層與層之間設置Cohesive 單元。遠離切削區的一側1 mm 寬的工件區域設置為完全約束。由于刀具的剛度遠大于工件，為節省計算時間，將刀具定義為剛體。刀具的具體結構參數見表2。通過控制刀具上參考點的移動和轉動以模擬銑削運動過程，銑削的工藝參數見表3。

圖2 銑削CFRP有限元模型Fig.2 Finite element model for milling CFRP

表2 刀具結構參數Tab.2 Tool geometry parameters

表3 切削工藝參數Tab.3 Cutting process parameters

網格的設置在涉及高變形問題的模擬中十分重要，CFRP 單層板的單元網格類型設置為C3D8R（8節點三維線性實體，減縮積分沙漏控制單元），層間Cohesive 單元網格類型設置為COH3D8（8 節點三維粘聚力單元），刀具網格類型為C3D4（4 節點線性實體）。網格尺寸大小的設置要考慮計算精度及時間效率的平衡，經過仿真測試，宏觀切削模型網格在0.1 mm以內精度較好，大于0.1 mm仿真精度急劇變差，故單層板單元網格大小設置為0.1 mm×0.1 mm×0.1 mm；層間單元厚度為0.01 mm，單元網格大小為0.1 mm×0.1 mm×0.01 mm；CFRP 層合板的單元數量為34 500 個。刀具為剛體，不參與計算，網格大小設置為0.3 mm，單元數量為76 000個。

刀具與CFRP 的接觸設置為面與節點（刀具的表面與工件的所有節點）的接觸，摩擦因數為0.5［19］。與此同時，為避免切削過程中工件內部單元相互嵌入，對整體模型采用自接觸。

模型中時間總長為0.29 s，整個模型需在16 GB運行內存的計算機上運行28 h。

2 實驗設計

為了研究銑削過程中加工損傷類型及分布，采用德瑪吉五軸加工中心DMU80T 對四種典型的纖維方向角的CFRP 層合板進行銑邊加工。實驗中所用的工件材料為恒神股份有限公司的CFRP 單向層合板，碳纖維型號為T700，質量密度為1.21 g/cm3，材料的其他性能參數見表4。

表4 CFRP材料性能參數Tab.4 Property parameters for CFRP

工件尺寸大小為250 mm×120 mm×2.5 mm。如圖3 所示，CFRP 層合板通過兩塊壓板固定以降低切削過程中振動，刀具采用Φ10 mm 硬質合金銑刀，銑刀結構參數見表2。銑刀通過逆銑的方式沿著工件的長邊緣不斷向前進給，工件厚度為2.5 mm，因而切削深度ap為2.5 mm，其他工藝參數見表3。采用Kistler9257B 三向測力儀對切削力進行測量，采用VHX-1500 超景深電子顯微鏡對加工表面形貌進行觀測。

圖3 銑削實驗設置Fig.3 Milling experimental device

3 仿真結果分析

3.1 切削力

圖4 為銑削CFRP 單向層合板的三向切削力隨纖維方向角的變化規律。由于仿真中模型厚度的增加會導致計算時間的急劇增加，因此實驗與仿真均取單位厚度的切削力（N/mm）進行對比驗證，其中實驗與仿真的銑削力分別取穩定切削區域的切削力峰值的平均值。通過對比切削不同纖維方向角的CFRP 產生的切削力可得，y向切削力（進給切削力）與z向切削力仿真與實驗吻合精度較高，誤差控制在20%以下，x向切削力仿真精度稍差。由于切削仿真是在刀具完全鋒利并沒有磨損的理想條件下進行的，因此仿真得到的切削力大部分相比實驗切削力偏小。

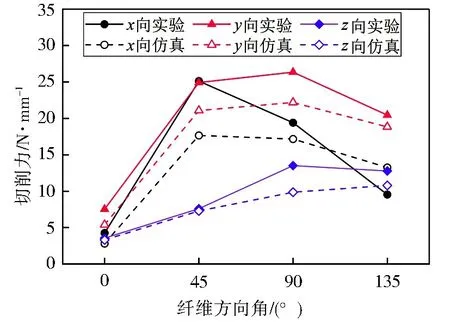
圖4 CFRP單向板切削力隨纖維方向角的變化Fig.4 Variation of cutting force for CFRP unidirectional laminates with fiber orientation angle

由圖4 可得，x向切削力和y向（進給方向）切削力均隨著纖維方向角的增大先增加后減小，但纖維方向角為45°時x向切削力最大，纖維方向角為90°時y向切削力最大。z向切削力隨著纖維方向角的增加呈增大趨勢，纖維方向角為90°和135°時z向切削力較大。如表5 所示，銑削過程中纖維切削角（纖維切削角為切削速度與纖維方向所成的夾角）是動態變化的，由于徑向切寬為1 mm，刀具直徑為10 mm，切削纖維方向角為0°的CFRP 時，纖維切削角為大鈍角（135°＜β≤180°），此過程破壞形式主要為水平方向的剪切破壞，故所需的三向切削力均較小；當纖維方向角為45°時，纖維切削角為小銳角（0°＜β≤45°），破壞形式主要為沿纖維方向的剪切破壞，x向與y向分力大致相等。而當切削纖維方向角為90°的CFRP時，纖維切削角為大銳角（45°＜β≤90°），纖維束大部分直接被切斷，故所需的y向（進給方向）切削力最大；纖維方向角為135°時，纖維切削角為小鈍角（90°＜β≤135°），破壞形式主要為彎曲斷裂，所需的切削力小于切削纖維方向角為90°的CFRP 時所需的切削力。

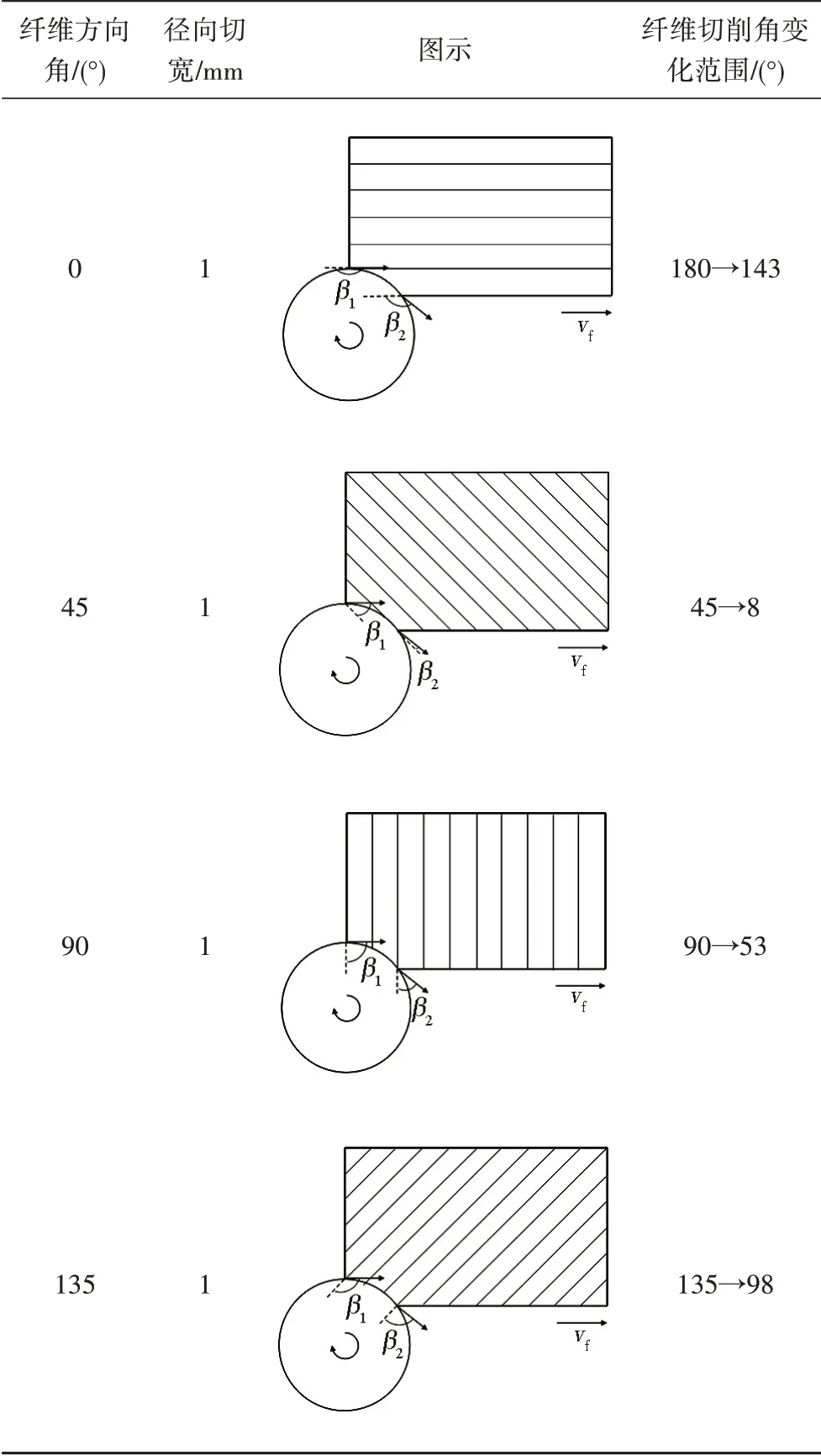
表5 不同纖維方向角下纖維切削角的變化Tab.5 Variation of cutting angle for CFRP unidirectional laminates with different fiber orientation angle

3.2 層間應力

在刀具切削CFRP 過程中，層內與層間均產生應力，如圖5所示，但由于層間單元的破壞應力低，層間應力先達到極值產生損傷，導致層間產生開裂，形成撕裂、分層等加工損傷。層間應力與加工損傷有密切的關系，但層間應力通過實驗很難測得，而利用有限元仿真中的Cohesive 單元可提取CFRP 在銑削加工過程中層間應力大小。

加工過程中層間應力隨著刀具的移動不斷變化，故本文選取與切削區有一定距離（保證整個切削過程未被切除）的4個單元（16個節點），如圖6所示，提取節點上的層間應力隨時間的變化曲線，取其16組數據的平均值作為層間應力大小的參考標準，在相同位置點的層間應力的平均值越大，說明層間損傷越嚴重。

圖5 切削過程中CFRP上的應力分布Fig.5 Stress distribution on CFRP during cutting

圖6 切削過程中CFRP上的應力分布Fig.6 Extraction point of interlaminar stress

經計算處理，圖7 為有限元模型中銑刀銑削CFRP 產生的層間應力隨纖維方向角的變化曲線，采用Mises等效應力表達層間應力大小［20］。

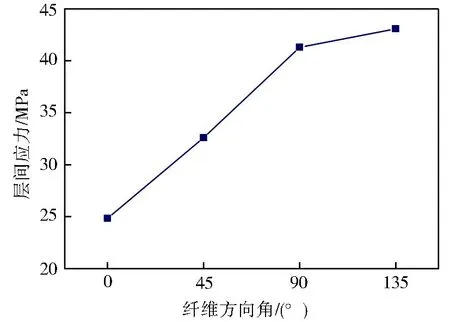
圖7 不同纖維方向角下層間應力變化Fig.7 Variation of interlaminar stress with different fiber orientation angle

由圖7看出，層間應力隨著纖維方向角的增加而增大。纖維方向角為0°層間應力最小，纖維方向角為135°時層間應力最大。纖維方向角為0°時，軸向力最小，相應法向正應力小，且切削過程容易從界面處斷裂，層間單元所受的剪切應力小，故層間Mises總應力最小。纖維方向角為45°時，軸向力與剪切力均增大，層間Mises 總應力增加。纖維方向角為90°、135°時軸向力差距不大，即法向正應力相近，纖維方向角為90°時，切削刃能及時切斷大部分纖維，但纖維方向角為135°時，纖維在刀刃擠壓作用下先發生彎曲，這使得層間單元所受的剪切應力最大，故層間Mises總應力最大。

3.3 層間損傷

CFRP由于層間結合強度低，在切削過程中易產生層間損傷，圖8為銑削CFRP層合板層間損傷模擬，由圖可定性的觀察出切削過程是否產生了層間損傷，但定量的去表征層間損傷的大小對于對比分析十分重要。

圖8 銑削過程分層損傷模擬Fig.8 Simulation of delamination in milling process

切削過程中，層間單元在切削力的作用下應力達到極值后會產生剛度退化，當剛度退化到0.99后，材料已基本失去承載能力，可作為層間損傷區域［8］。故本文將剛度退化系數達到0.99的區域作為層間損傷區域。針對銑削加工的層間損傷提出二維層間損傷因子。二維層間損傷因子是層間損傷區域的面積與被切除材料面積的比值，如圖9所示。

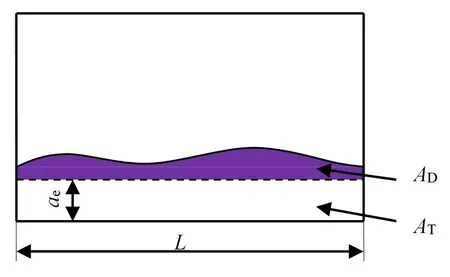
圖9 二維層間損傷因子表征示意圖Fig.9 Schematic diagram of 2D interlaminar damage factor characterization

二維層間損傷因子（FD）的表達式如下所示：

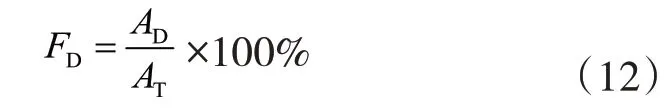
式中，AD表示層間損傷區域的面積，AT為被切除材料的面積，AT=ae×L，其中ae為側銑加工時的切寬，L為工件被加工一側的長度。

在右旋銑刀銑削纖維方向角為45°的CFRP有限元結果中，提取上、下二層Cohesive單元的剛度退化如圖10所示，層間損傷區域的面積AD為紅色虛線內的白色區域及紅色區域面積之和。利用Matlab軟件對切削穩定區域的層間損傷圖片進行二值化處理，計算出層間損傷面積AD占圖片面積的比值以求得分層損傷面積AD的實際大小，進而求得二維層間損傷因子FD。對四種纖維方向角的有限元模型中切削穩定區域后處理得到各自的二維層間損傷因子FD見圖11。

圖10 不同位置的層間損傷Fig.10 Interlaminar damage in different position

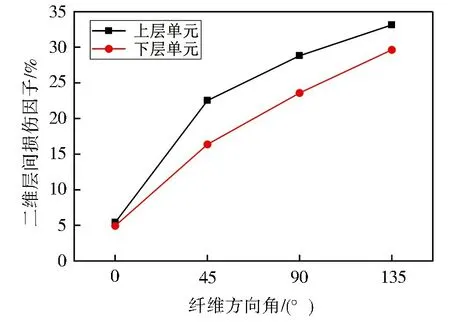
圖11 二維層間損傷因子Fig.11 2D interlaminar damage factor

圖12 纖維方向角對層間損傷的影響Fig.12 Effect of fiber orientation angle on interlaminar damage

由圖10 與圖11 可以看出，當刀具切削四種纖維方向角的CFRP 時，均呈現上層層間單元損傷大于下層層間單元損傷的規律。這是因為刀具為右螺旋銑刀，切削時切削刃產生一個向上的切削分力CFRP 上表層的上部沒有約束，故層間損傷最大，層間損傷后產生毛刺、撕裂等加工損傷。CFRP 下表面在切削應力擠壓下也有部分失效，但上側有材料的約束，故下表面的層間損傷較小。

由于分層、撕裂、毛刺等加工損傷集中在工件的上表面，故針對工件的上層層間單元進行分析，由圖11 和圖12 得層間損傷區域隨纖維方向角的增加而增大。纖維方向角為0°時，層間應力最小，幾乎沒有層間損傷，加工表面質量最好；纖維方向角為45°時，受沿著纖維方向剪切失效的影響，纖維與基體界面開裂，但由于纖維方向角的影響，未切除的纖維束在刀具進給方向的反方向，纖維束不易被掀起，CFRP內部產生較小的層間損傷，已切削的部分則因纖維與基體界面開裂形成絲狀毛刺。纖維方向角為90°時，大部分纖維束被直接切斷，未切斷的纖維束由于纖維束與刀具進給方向成90°，受剪切應力的作用產生層間損傷，纖維束被掀起，形成撕裂以及片狀毛刺，層間損傷較大；纖維方向角為135°時，未切除的纖維束在刀具進給方向的同方向，大部分纖維束不能被切斷，受彎矩應力的作用CFRP 內部沿著纖維方向產生層間損傷，纖維束基本都被掀起形成撕裂和片狀毛刺。由此可得，纖維方向角為135°時，層間損傷最大。

4 結論

通過建立的包含CFRP 層間、層內單元損傷演化的三維銑削CFRP 有限元模型，探究了切削力、層間應力與層間損傷隨纖維方向角的變化關系，同時針對層間損傷基于剛度退化理論提出了二維層間損傷因子，實現了動態切削過程中的層間損傷仿真預測。已驗證的三維銑削CFRP 有限元模型可用于對于刀具結構以及加工工藝參數的優化。通過仿真結果分析，得出以下結論：

（1）通過對比宏觀銑削模型與實驗測得的切削力可知，x向和y向切削力均隨著纖維方向角的增大先增加后減小，纖維方向角為90°和135°時z向切削力較大。仿真與實驗結果變化規律一致。

（2）層間應力隨著纖維方向角的增加而增大，纖維方向角為135°時，層間應力最大。

（3）層間損傷與層間應力隨纖維方向角的變化趨勢一致，纖維方向角為0°時，層間損傷最小；纖維方向角為135°時，層間損傷最嚴重。