觀察、操作、想象：讓空間觀念發展清晰可見
——“‘圖形的運動’練習課”教學實踐與評析

□郭建平 執教 顧志能 評析

【課前思考】

《義務教育數學課程標準（2011 年版）》（以下簡稱《課程標準》）中有一道例題（例35）引發了我們的關注。這道例題的名稱為“圖畫還原”（如圖1），要求是“打亂由幾塊積木或者幾幅圖畫構成的平面畫面，請學生還原，并利用平移、旋轉記錄還原步驟”。例題說明指出：通過實際操作進一步理解平移和旋轉，不僅能增加問題的趣味性，還可以讓學生感悟幾何運動也是可以記錄的，體驗選取最佳方案的過程。

圖1

這道題素材簡單有趣，吸引眼球，正適合訓練學生的觀察能力。其形式為圖畫還原，學生操作方便，動手能力、探究能力可得到錘煉；其內涵涉及平移、旋轉，學生可綜合運用這些知識解決問題，應用能力也可得到發展……更為重要的是，這是一個發展學生空間觀念的絕佳載體。比照《課程標準》中對空間觀念的刻畫描述，我們發現，這道題既可以引導學生想象圖形之間的位置關系，又可以讓學生去描述圖形的運動和變化，還可以讓學生根據數學語言的描述畫出圖形。

基于以上思考，我們決定以例35為藍本，開發一節“圖形的運動”練習課，其目標指向主要有兩點：以問題解決為驅動，使學生鞏固對平移、旋轉和軸對稱三個知識（技能）的掌握；通過豐富的學習形式（活動），讓學生充分經歷觀察、想象、比較、綜合等學習過程，實現空間觀念的有效發展。

需要特別說明的是，例35 只要求使用平移和旋轉，若把同樣是圖形運動方式的軸對稱納入其中，則知識更完備，內涵更豐富，也更能體現“圖形的運動”練習課該有的要求。

【課堂實錄】

一、喚醒舊知，引入新課

1.回憶舊知，揭示課題

師：同學們，你們已經學過圖形運動的哪些知識？

（通過交流，學生回憶起“平移”“旋轉”和“軸對稱”三種不同的圖形運動方式）

師：今天我們要進一步運用這些知識研究圖形的運動。

2.創設情境，激發興趣

師：一個笑臉拼圖，有兩塊被打亂了（如圖2）。1號圖形要回到原來的位置，可以怎么運動？

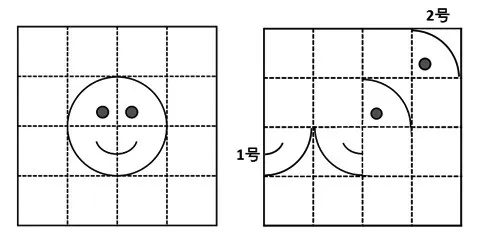
圖2

（學生觀察后回答“向右平移2 格”，教師強調“平移要關注方向和距離”，課件演示還原過程）

師：除了平移能使1 號圖形回到原來的位置，還有其他的方法嗎？

（絕大部分學生想不到，教師鼓勵并引導學生往“軸對稱”方向思考）

師：如果把這條線當作對稱軸，1號圖形經過軸對稱變化以后會到哪里？（課件呈現AB對稱軸，如圖3，教師引導學生想象，課件跟進演示）

師：從現在這個位置還原到原來的位置，還要怎么運動呢？

生：再軸對稱變化一次。

（課件呈現CD 對稱軸，教師引導學生想象，再動態演示）

（評析：本環節讓學生通過觀察和想象，完成簡單的圖形還原，既有效地喚醒了學生對圖形運動相關知識的回憶，又讓學生感受到可以靈活選擇不同的運動方式來還原圖形。）

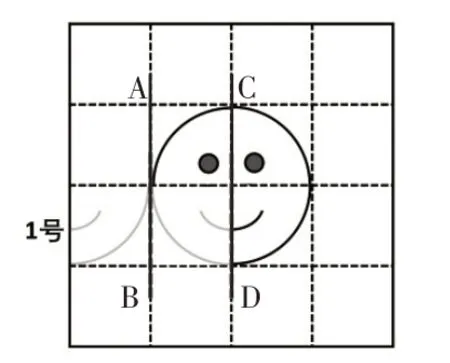
圖3

二、動手操作，深入探究

1.情境跟進，自主探索

師：2 號圖形要回到原來的位置，可以怎么運動？（如圖4）

圖4

2.方法反饋，分享思維

（當學生各自找到還原的方法后，教師組織學生進行反饋）

生：我把2 號圖形原地旋轉，然后向左平移2格，再向下平移1格。（學生上黑板操作演示）

師：怎么原地旋轉？（根據學生回答，引導學生明白在講旋轉時要講清楚旋轉中心、方向和角度）

生：我是把2號圖形向下平移1格，再向左平移1格，再沿左側線軸對稱1次，就還原成功了。

（教師請聽懂的學生再次上臺操作演示，確認能還原）

生：我的方法不一樣。我先把2號圖形向左平移2 格，再繞點逆時針旋轉90°。（學生講的點是格子圖上的一個交點。他上黑板演示到這一步時，教師適時引入“數對”概念，引導學生講得更明白）

……

（評析：本環節引導學生靈活運用圖形運動的三種方式解決問題，通過展示交流多樣化的還原方法，讓學生打開了思路，分享了經驗，豐富了思維。）

小學數學教育信息化是新時代教育的必然選擇。當下，部分教師素質較低，與學生溝通能力較差，對于小學數學教育信息化的理念和方法，并沒有較好地理解，以至于在教育的效率和質量上，都沒有獲得良好的提升，最終產生的教育問題較為顯著。此種情況下，小學數學教育信息化的策略部署，必須按照科學、合理的模式來進行，對于多方面的問題和不足進行積極的彌補，促使未來的教育工作水平能夠獲得更好的提升和進步。

3.再次體驗，規范記錄

在展示了學生的多種還原方法之后，教師也用課件演示了另一種方法（如圖5），并運用數學語言規范地記錄下來，如“2 號圖形繞點（3,3）逆時針旋轉90°，再向左平移1 格，再向下平移1格”。

教師鼓勵學生選擇自己喜歡的一種還原方法，再操作一次，并用這樣的數學語言記錄下來。

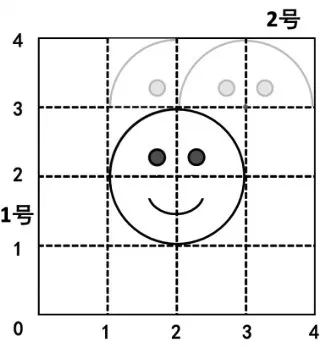
圖5

4.游戲支撐，深化探究

圖6

引入游戲，告知計分規則（如圖6）。教師計算出自己那種方法的得分為3 分；學生計算各自所記錄方法的得分，統計各種分值的人數（基本上是3分或4分）。

出示游戲規則——分數低者為勝（分數低說明步驟少，思維簡潔），引導學生探究是否有低于3分的還原方法。學生可以借助材料單獨操作，也可以合作探究，實現還原后及時記錄方法。

（評析：通過游戲計分的介入，刺激了學生的求勝欲和好奇心。學生積極主動地探究是否有2 分乃至1分的還原方法，目標驅動著學習走向深入。）

5.分享最佳，引導想象

生：2 號圖形繞（3，3）逆時針旋轉180°，再繞（2，3）順時針旋轉90°，我這樣是2分。

師：想象一下，這位同學的幾個步驟，能否成功還原。（其他學生想象，教師適時用實物演示作為支撐，確認2分成功）

生：先繞（3，3）順時針旋轉180°，然后再繞（2，3）順時針旋轉90°，也是2分。

生：我發現同一個圖形，繞同一個點順時針和逆時針旋轉180°，結果是一樣的。

師：你太厲害了！大家再關注這個圖形，繞（3，3）向兩個方向旋轉180°，想象一下，結果是怎樣的？

生：我們是以那條斜線，即數對（4，2）和（2，4）的連線為對稱軸進行1 次軸對稱后，再旋轉的，也是2分。（學生上黑板點出那條斜線）

師：同學們，想象一下，沿這條線軸對稱變換，會怎么樣？再旋轉呢？

（學生想象，教師適時跟進演示）

生：我們是通過兩次軸對稱運動實現還原的。先以2 號圖形的左側線為軸，軸對稱1 次，再以（3，2）和(1，4)的連線為軸，軸對稱1次，就成功了，2分。（教師同樣引導學生想象，再適時跟進演示）

……

（評析：整個活動圍繞2分的還原方法展開，通過讓其他學生聽懂、想明白某種方法，逐步幫助學生擺脫實物操作，提升想象能力，使得思維實現從具象到抽象的慢慢過渡。）

三、自主設計，深入想象

師：笑臉圖已經恢復正常了，現在如果讓你任選其中的一塊拼圖，打亂位置，你打算放到哪里？它又可以怎樣還原呢？

（教師請一學生上黑板，隨意打亂一塊拼圖，任意放置在一個位置上，然后引導全班學生觀察拼圖，要求僅憑想象，思考它還原的步驟和方法）

（評析：放手讓學生創設學習素材，迫使學生擺脫實物操作，只能憑借空間想象去完成任務。這樣的安排，讓學生的想象能力得到了再訓練和再提升，雖然有難度，但是體現了思維發展的梯度要求。）

四、課堂總結，暢談感受（略）

【課后反思】

一、精細的觀察，使學生感知到位

認識幾何圖形的性質特征是形成空間觀念的基礎。而兒童獲得幾何圖形性質特征的認識，往往是從對具體對象的觀察開始的。在本課中，教師以“笑臉拼圖”為素材，尤其是以還原打亂了的拼圖為任務，引發學生主動聚焦圖形的特征——整幅圖的特征、每小塊的特征、運動變化的特征。每一次的還原，無論是1號圖形經過平移、軸對稱的變化，還是2號圖形可采用的多種形式的變化，甚至是任意打亂一塊拼圖后的還原，教師都先讓學生展開精細的觀察，然后再適時跟進操作、演示或想象。正是在對圖形初始狀態、目標狀態、變化過程的精細觀察和深入比較中，學生不斷感知圖形的特征，感知三種運動方式的特征，頭腦中由此留下深刻的印象。這為他們空間觀念的發展奠定了堅實的基礎。

二、充分的操作，讓學生表象清晰

兒童在學習幾何圖形時，并不是簡單地靠識記去把握圖形的名稱、形狀、特征及變化，更為有效的是靠操作活動，直觀和真實地去感知概念，并從中構建空間觀念。正是基于這樣的認識，教師在這節課中安排了多次操作活動。如2號圖形的還原，就是先讓每個學生動手去操作（為此給每個學生精心準備了操作材料），在操作中再讓學生結合觀察，調用經驗，積極嘗試，尋找到不同的還原方法。經歷這樣的過程，學生的大腦中就留下了關于2號圖形運動的痕跡，而這種痕跡，隨著語言表達、課件演示等的跟進作為支撐，不斷完善與清晰，最后深深地印在學生的頭腦中，這就是表象的建立。同樣道理，關于2號圖形能否以低于3分的方法還原，也讓學生先動手操作再交流，觸覺越充分，學生的感知越到位，表象也就越清晰。

三、豐富的想象，令學生印象深刻

圖形與幾何學習中的想象，指的是在頭腦中（心理上）對幾何形體的形狀、結構、特征以及位置關系，有意識地進行加工改造乃至全新創造的過程。這是一種高級的思維活動。這種思維能力的提升需要借助合適的載體進行針對性的訓練。本課圍繞想象做了不少文章。一是多處設置想象環節。從課中可以看到，1號圖形的軸對稱還原先讓學生想象；2 號圖形的2 分還原在學生講方法時其他學生想象（多次）；任意打亂拼圖后憑想象還原。二是想象要求拾級而上。從上述幾個步驟中不難看出，想象的要求是從直觀（視覺、操作）支撐到半支撐再到脫離支撐，不斷進階逐步提升的。正是有了這樣的多點分布、有序推進，學生的空間想象能力才能得到明顯的發展。

當然，空間觀念的發展，除了上述三個要素之外，合適的材料（學具、教具、課件等），有效的交流（師生、生生等），靈活的形式（探究、推理等）……也能有效促進學生對圖形的感知和把握。教學中，只要我們聚焦目標，精心設計，合理實施，學生空間觀念的發展就一定卓有成效。