“圖解數學”，“小老師”的好幫手

□陳 云

“小老師”是近年來出現的一種新型教學方式。它一方面可以更好地彰顯學生的主體價值，激發學生自身的學習主動性和學習潛能，另一方面也能更好地發揮同伴互助的教學功能。“圖解數學”是用圖或畫的方式來解釋數學的結論或原理，實現小學生數學思維可視化的一種有效方式。它是學生相互交流、自主建構的重要載體，可以成為“小老師”分析講解、反思修正的常用手段，從而促進自身數學能力的提升，也有助于啟發其他同學。

一、圖解數學讓“小老師”的見解清晰可見

讓學生做“小老師”是落實學生主體地位的一種做法。每個學生都希望有機會當“小老師”，為了獲取這樣的展示機會，學生會主動、積極地對外部信息進行深度認知以及再加工。這一過程看似簡單，其實對數學信息從初步感知到完全理解，再到外化展示，對于小學生來說是一個極其復雜的過程，需要“小老師”進行辨別、比較、判斷和加工。要較好地完成這一任務，學生除了要具有良好的語言基礎外，還必須掌握必要的技巧。“圖解數學”就能恰到好處地幫助學生對數學信息中的內容進行有效梳理，例如：借助圖示提取重要數學信息、借助圖示表征關鍵的數量關系等。

在蘇教版二年級上冊“認識平均分”的教學中，教師追問：什么是平均分？對于這樣的問題，學生有“似曾相識”的熟悉，也有“霧里看花”的模糊，如果要求“小老師”來談談自己的想法，不借助一定的外顯形式，確實很難表述，學生說來說去就是一句“分得同樣多”，再不知如何解釋。這樣的回答并不足以讓其他同學有更多收獲，也很難對除法的意義和除法可能存在的兩種情況（平均除、包含除）進行有效區別。但如果我們把這樣一個寬泛的問題讓學生用圖解的方式使其具體化、形象化：“什么是平均分？把你認為是平均分的故事寫出來或畫出來。”學生從自己的生活中去搜索平均分的實際問題，然后努力選擇合適的表征方式把問題記錄下來，在作業展示環節，“小老師”有了抓手，講解起來就會底氣十足：“媽媽買來12顆糖果，如果哥哥、我和妹妹每人分得的同樣多，我們每人可以分到4顆糖果。你看，我們3 個人要分得同樣多，這就是平均分，可以說是平均分給哥哥、我和妹妹。”“張老師有8只氣球，每人給2只，張老師的氣球可以分給幾個人？每人2只就是你2只、他2只、我也2只，一直分，分給了4 個人，這樣每個人都得到2 只，就是同樣多，所以叫平均分（如圖1）。”……很顯然，有了圖解，“小老師”的表達就顯得“有血有肉”、活靈活現，對低段學生建立“平均分”的表象很有幫助，也能啟發其他同學想到各種平均分的實際問題。

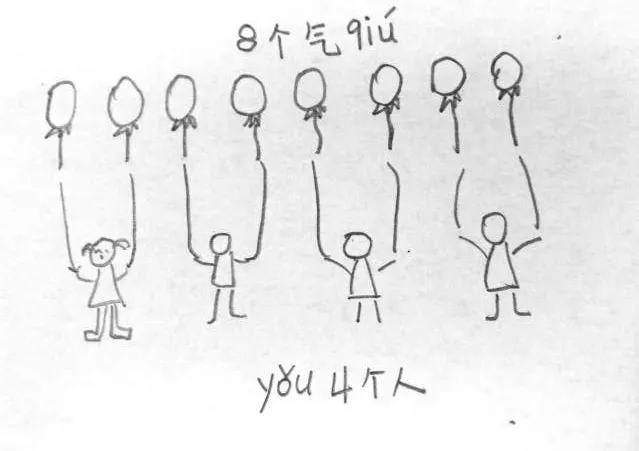
圖1

小學生的思維是由具體形象思維逐漸發展為抽象思維的一個質變的過程，需要一定的教學手段和工具媒介助力。一些直觀的圖示、表格在學生思維轉變中能起到重要的作用。如上，憑借直觀的圖解，學生對抽象的“平均分”問題有了真實的、可觸摸的理解。

二、圖解數學讓“小老師”的分析絲絲入扣

直覺是指在經驗和已有知識的基礎上，不經過邏輯推理而直接迅速地認知事物的思維活動。在數學學習過程中，學生很容易用“直覺”判斷一個結論是否正確，習慣于遵從“直覺思維”模式，不太愿意對數學問題做理性分析。之所以出現這種情況，是因為“直覺”也會在很多時候讓學生做出正確的判斷，這固化了學生的“直覺規律”，相應的也導致學生發生一些常見的錯誤。教師要尋求一種方式讓學生養成一種良好的習慣，即在自己沒有完整思考的情況下，不輕信、不盲從“直覺”的答案。“圖解數學”就是一種可用的方式。“圖示”作為一種特有的數學語言，既可以解釋概念，也可以對解題策略進行分析，一定程度上能幫助學生克服錯誤的直覺反應，讓問題的分析過程和推理過程更有深度。

例如蘇教版五年級上冊“小數的再認識”的教學，教師要幫助學生真正理解小數，感知小數的記數是“位值記數法”的拓展，小數是遵循整數記數規律的一種新的數。但是，如果只是簡單地進行十進分數與小數的互化，“小老師”恐怕自己都未必明白為何等于0.72，只是憑直覺說出7分米2厘米=米=0.72米，這不是思考的結果，而是依照教師之前給出的情景，“套路”出的答案。那寫成三位小數，是0.072 還是0.720 呢？為了幫助“小老師”進行理性分析，教師可為學生創造“圖解數學”的經歷：用米尺測量出張老師的身高，并用小數表示出來，也可用其他圖示解釋你的思路（如圖2）。有了“圖解”的經歷，“小老師”的分析便能入“理”三分：“我是這樣想的，10米平均分成10份，每份就是1 米，1 米平均分成10 份，每份就是0.1 米，7 個0.1米就是0.7 米；接著往后分，這里有點小，看不出來了，但我們可以想象，0.1 米再分就是0.01 米，因為它們都是10份、10份地分下去的，這里大約是2個0.01米，全部合起來就是1.72米。”（如圖3）“我覺得1米平均分成10份，1份就是米，也是0.1米，0.1就是1的個0.1米就是0.7米；再往后把0.1平均分成10 份，其實就是把1 米平均分成100 份，每份是米，也就是0.01 米就是0.01，2 個0.01米就是0.02米。我覺得好像還多了一半，這里分不下了，我把它畫在右邊。我們可以想象一下，0.01接著平均分，每份應該是0.001米，我感覺在中間，就算5份吧，那就是0.005米，合起來就是1.725米。這里的0.1，0.01，0.001之間都是10倍、10倍的關系，和還有整數的1000，100，10，1之間的關系都是一樣的。”（如圖4）

圖2

圖3

圖4

“圖解”過程中，“小老師”的思考路徑清晰可見，能借助平均分的操作，把尚未正式學習的小數單位解釋得不那么抽象了。因為學生很巧妙地把小數這種計數方式和整數進行了有效的溝通，10份、10份地逐次分下去，也就從左往右逐次排列下去，成為0.1，0.01，0.001。再結合十進分數的結構來解釋小數，把整數、小數、分數進行了聯系，實現了零散知識體系化。當圖示中0.01平均分成10份時，學生沒辦法畫了，但能根據相應的原理進行想象，推理出接下來分的過程和結果，可見學生的分析已經突破“直覺”，較好地彌補了文字描述無法在大腦中呈現清晰圖像的缺陷，很大程度上提升了“小老師”講解的效果。

三、“圖解數學”讓小老師的反思有據可依

維果茨基說過，人所特有的心理過程都是由語言、標志和符號這樣的心理工具充當中介的，這種以符號系統為中介的高級心理機能需要由外部集體活動內化而成。也就是說，學生最初是有自己的想法的，這些想法可能對、可能錯，也有可能是“半對半錯”，不足以實現從知識的理解到策略的形成。策略的形成需要經歷一個過程，在這個過程中需要自我的反思和與同伴的交流。學生參加小組或全班的學習活動，須借助各種符號展開交流，以幫助學生實現自我完善。

例如在“平均數”問題的教學中，小學階段較為常見的算術平均數的計算，就是兩個數的算術平均數個數的算術平均數受到算術平均數算法的影響，在“用單價10元的牛奶8千克和單價5元的果汁2千克，混合成牛奶果汁，每千克應該以什么價格出售？”這類加權平均數的問題中，一位“小老師”振振有詞地表達了自己的觀點：這里是求價格的平均數，所以只要找到價格10元和5 元就可以了，（10+5）÷2＝7.5 元，應該以7.5元的價格出售。對于這樣的講解，學生中漸有唏噓聲，很顯然，原來僅8千克牛奶就要80元，現在加上果汁才75 元，一定有問題。可是，問題出在哪里？算術平均數的算法根深蒂固地纏繞著學生的思維，學生必須借助圖解，把整個思路重新梳理，才能“破繭成蝶”。于是，教師引導學生反思：結合平均數學習的過程，畫出10千克果汁牛奶的價格如何平均。有“小老師”從平均數最初學習時用到的“移多補少”中受到啟發，給出了如圖5的解釋，這給其他同學一個啟發：原來這里不是1 個10 元和1 個5 元平均，而是8 個10 元和2 個5 元在平均。其他的同學也逐漸打開思路，給出了如圖6 的解釋，這為平均數的計算過程（10×8+5×2）÷10做了很好的直觀詮釋。借助思考路徑的圖解過程，“小老師”終于意識到最初的“振振有詞”是欠缺考慮的，并真正接受和理解了加權平均數與算術平均數的“異”與“同”。

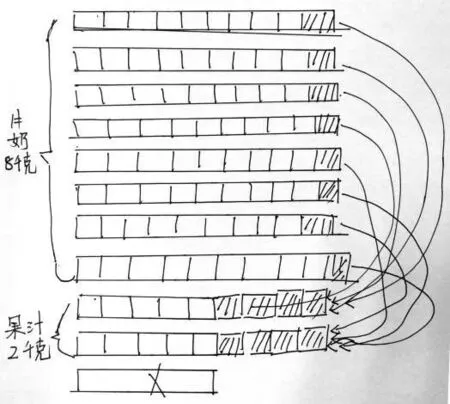
圖5

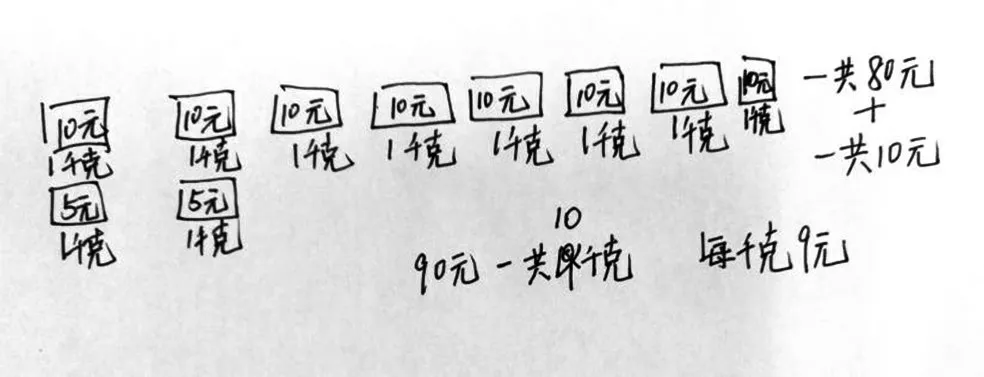
圖6

“小老師”登上舞臺，借助“圖解數學”，用直觀的圖形顯化思維，在合作交流中用精準的語言闡述思考過程，能發展學生的數學思維，提升學生的數學能力。