蘭州地鐵地溫分布特性及其演化規律

張虎元，朱江鴻，馬國梁，甄作林,3，蓋玉璽

(1.蘭州大學 土木工程與力學學院， 甘肅 蘭州 730000；2.蘭州大學 西部災害與環境力學教育部重點實驗室，甘肅 蘭州 730000；3.中鐵西北科學研究院有限公司， 甘肅 蘭州 730000)

地鐵地溫是地鐵暖通空調系統優化設計的主要參考指標[1-3]，合理設計地鐵暖通空調系統，高效節能地調節地下空間的溫度[4-5]，對于提高乘客的舒適度，節約地鐵運營成本具有重要的實際意義。

關于地溫的研究已有不少成果，主要集中在地熱學，包括礦井圍巖地溫、地源熱泵與地溫關系、氣象學等[6-9]。其中，針對地鐵地溫研究較少，只有一些文獻針對南京和西安等地的地鐵進行了研究，積累了一些數據。Xiang等[10]在分析地鐵地溫過程中，只給出了恒溫層的溫度為20 ℃。胡增輝等[11-12]實測了南京地鐵地溫，運用反演公式計算得到了地層土體的導熱系數，并采用數值模擬的手段分析圍巖傳熱范圍的影響因素，探究了地鐵隧道圍巖的傳熱機理。任建喜等[13]在西安地鐵沿線4個典型地貌單元布置9個鉆孔，觀測得到了不同地貌單元地層的恒溫層位置和地層地溫的分布規律，為西安地鐵暖通空調系統初步設計提供參考。

蘭州地鐵，處于我國西北高海拔的黃土高原地區，其所在地層與我國其他地方的地鐵地層不同。目前，關于蘭州地鐵地溫的分布規律研究相對缺乏。確定蘭州地鐵初始地溫(隧道開挖前的地溫)及運營條件下蘭州地鐵系統與初始地溫的相互作用規律，為今后蘭州地鐵運營過程中暖通空調的優化提供可靠的參考依據，可為高海拔地區地鐵空調工程的初步設計提供參考。因此，本文實測蘭州地鐵所在地層全年的初始地溫，分析其變化規律，提出蘭州地鐵初始地溫預測模型公式；并采用非穩態傳熱的數值模型，探究運營條件下蘭州地鐵圍巖溫度演化規律。

1 工程概況和現場監測方法

1.1 工程概況

根據蘭州市城市規劃和軌道交通線網規劃，蘭州地鐵分布在蘭州盆地內部的河谷地帶，由河谷高階地和河谷平原組成，地貌上屬于侵蝕—堆積河谷平原。地形較為平坦，其中包括黃河Ⅰ—Ⅳ級階地和漫灘。

蘭州地鐵沿線分布的圍巖地層主要有第四系全新統雜填土、素填土、黃土狀粉土、粉質黏土、粉細砂和下更新統卵石地層。土層一般為可塑—軟塑狀態，砂層稍密—密實，潮濕—飽和，卵石層稍密—中密，地層穩定，可作為圍巖和地基持力層，場地土的類型多為中硬場地土，部分為中軟場地土，場地類型為Ⅱ類。

1.2 監測斷面及測點布置

初始地溫監測斷面位于甘肅省蘭州市蘭州西客站(蘭州地鐵沿線重要車站之一)附近，與隧道水平距離為50 m左右，以保證地鐵隧道施工過程對監測地溫無影響，海拔高程為1 524.36 m。

根據地鐵隧道底板埋深為19.5～21.8 m，測點的最大深度設置為23 m。從地表開始，往下每隔1 m設置1個測點，測點埋深依次為1，2，3，…，23 m，命名依次為T1，T2，T3，…，T23，如圖1所示。

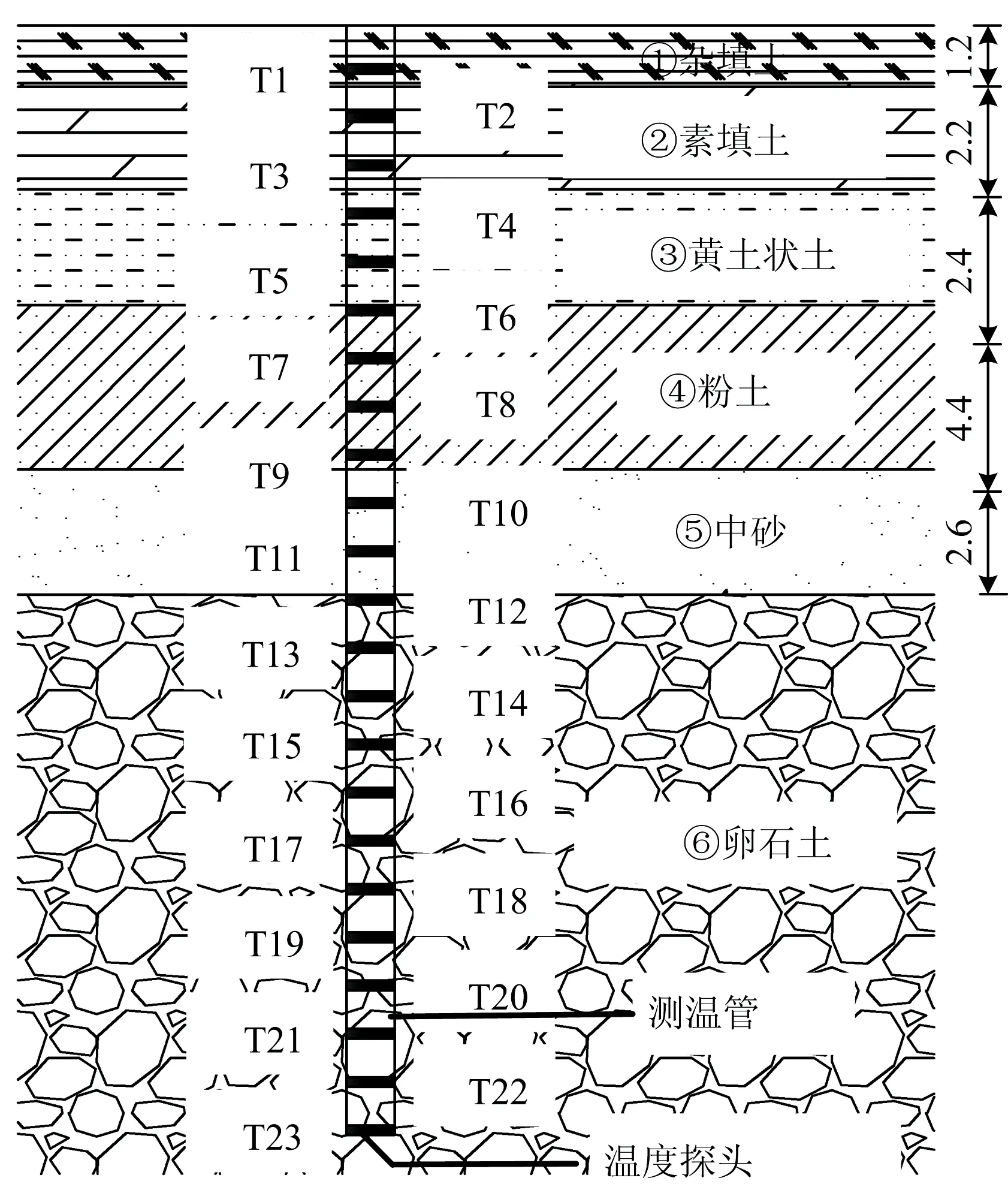
圖1 地溫測點布置(單位：m)

1.3 監測時間

監測從2017-03-25開始，至2018-03-17停止，共1年，測量周期為7 d·次-1。這1年4個季節的起止時間為：春季，2017-03-21—2017-06-20；夏季，2017-06-21—2017-09-22；秋季，2017-09-23—2017-12-21；冬季，2017-12-23—2018-03-20。

1.4 監測儀器

地溫監測儀器主要有溫度傳感器、溫度采集儀器，如圖2所示。溫度傳感器是自制的，由1/3B級JUMO四線制pt100鉑熱電阻、四線制四氟屏蔽導線、溫度探頭和插頭組成，精度為0.01 ℃，具有耐250 ℃高溫、耐-50 ℃低溫、耐腐蝕的功能，見圖2(a)。每個測點埋入1個溫度傳感器的探頭。溫度采集儀器采用wKc-988數字測溫儀，見圖2(b)，測溫范圍為-20～100 ℃，分辨率為0.1 ℃。

圖2 監測儀器

1.5 儀器校準

為了保證溫度測量的準確性，所有溫度傳感器在埋設之前進行溫度校準。在正式測量初始地溫之前，在冬季時測量了蘭州地鐵埋深1 m處的初始地溫，發現最低值大于0 ℃，并且蘭州環境氣溫不會超過50 ℃，則校準范圍為0～50 ℃。在溫度校準時，0～15 ℃的溫度環境在DW-40L262低溫冷藏箱進行，15～50 ℃的溫度環境在SHZ-88水浴恒溫震蕩器進行，低溫冷藏箱和水浴震蕩器的溫度通過多個溫度計驗證，準確性良好。圖3所示為溫度傳感器的室內溫度校準曲線，橫坐標實際溫度為低溫冷藏箱溫度或水浴溫度，縱坐標測量溫度為溫度采集儀器測試溫度傳感器的讀數。從圖3可以看出，測量溫度與實際溫度具有良好的線性關系，測量溫度=實際溫度+四線制四氟屏蔽導線的長度×0.3。測量溫度與實際溫度之間的誤差是由四線制四氟屏蔽導線的電阻造成的，是不可避免的[14-16]。因此，現監測得到的地溫數據，需要通過室內溫度校準曲線(圖3)進行校正，校正后的數據才是監測位置的真實溫度。

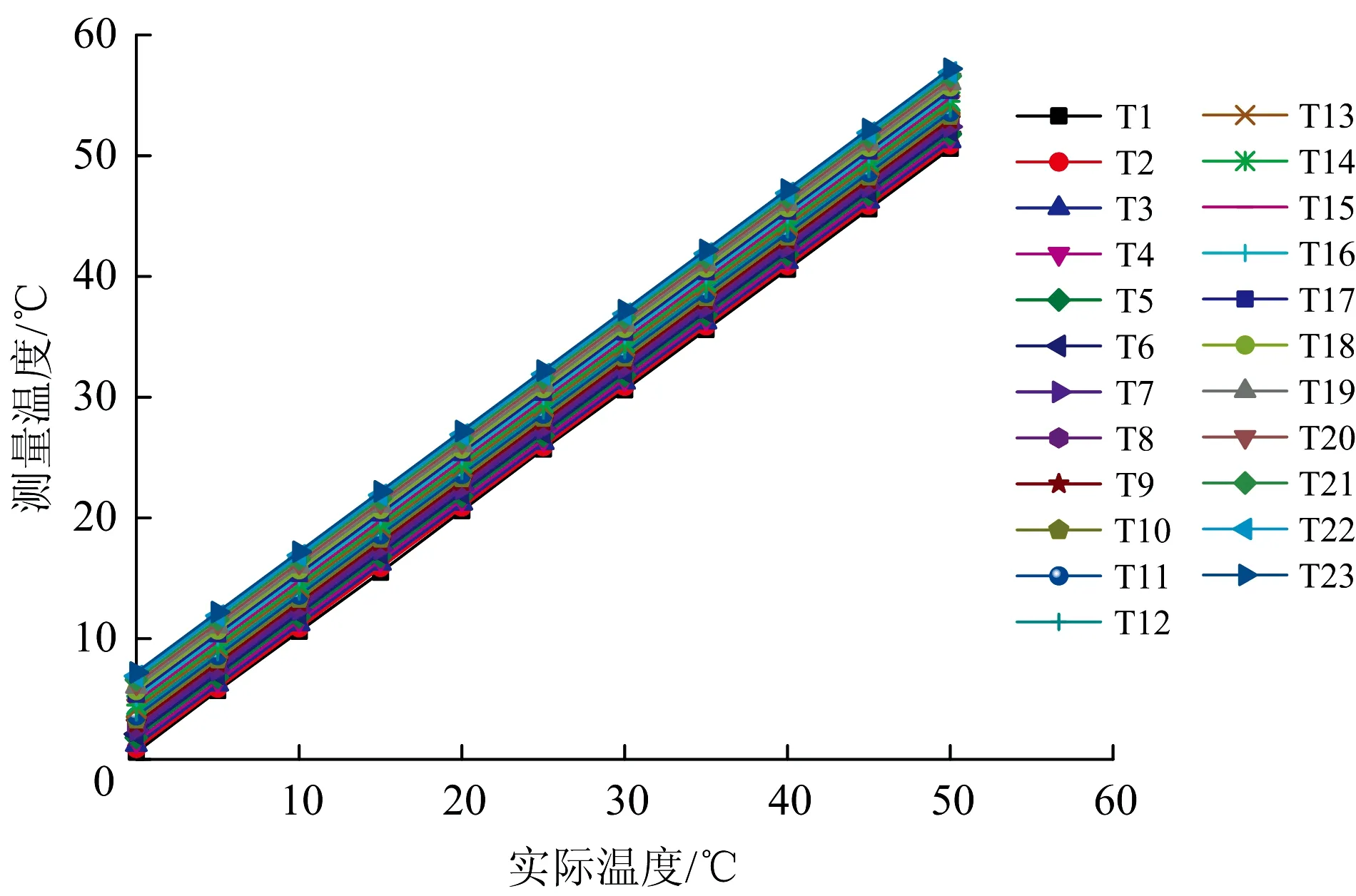
圖3 溫度傳感器室內溫度校準曲線

2 初始地溫監測結果

2.1 環境氣溫分布規律

環境氣溫不同，則地鐵初始地溫不同，并且不同深度的初始地溫隨著環境氣溫的變化會表現不同的變化規律，因此，應先分析環境氣溫的變化規律。

不同季節日平均氣溫隨時間的變化規律如圖4所示，圖中橫坐標軸時間表示1個季節從頭至尾的依次天數。從圖4可以看出：在春季，日平均氣溫整體呈上升趨勢，最初的日平均氣溫為10 ℃左右，最后的日平均氣溫可達到23 ℃左右，季平均氣溫為16.5 ℃；在夏季，日平均氣溫剛開始整體呈上升趨勢，最高可達31 ℃，然后呈下降趨勢，最末在18 ℃左右，季平均氣溫為22.8 ℃；在秋季，日平均氣溫整體呈下降趨勢，范圍在-3～19 ℃，季平均氣溫為6.9 ℃；在冬季，日平均氣溫整體呈現下降、上升、再下降(最低可達-10 ℃)、然后再上升的趨勢，最末在13 ℃左右，季平均氣溫為0.4 ℃。

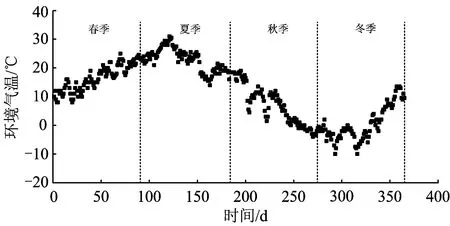
圖4 不同季節日平均氣溫隨時間的變化規律

2.2 不同季節地鐵初始地溫分布規律

蘭州地鐵1年4個季節初始地溫隨埋深的變化規律如圖5所示。結合圖5和圖4可以發現初始地溫與環境氣溫、埋深的關系，以及其平均值的分布規律，分別如下。

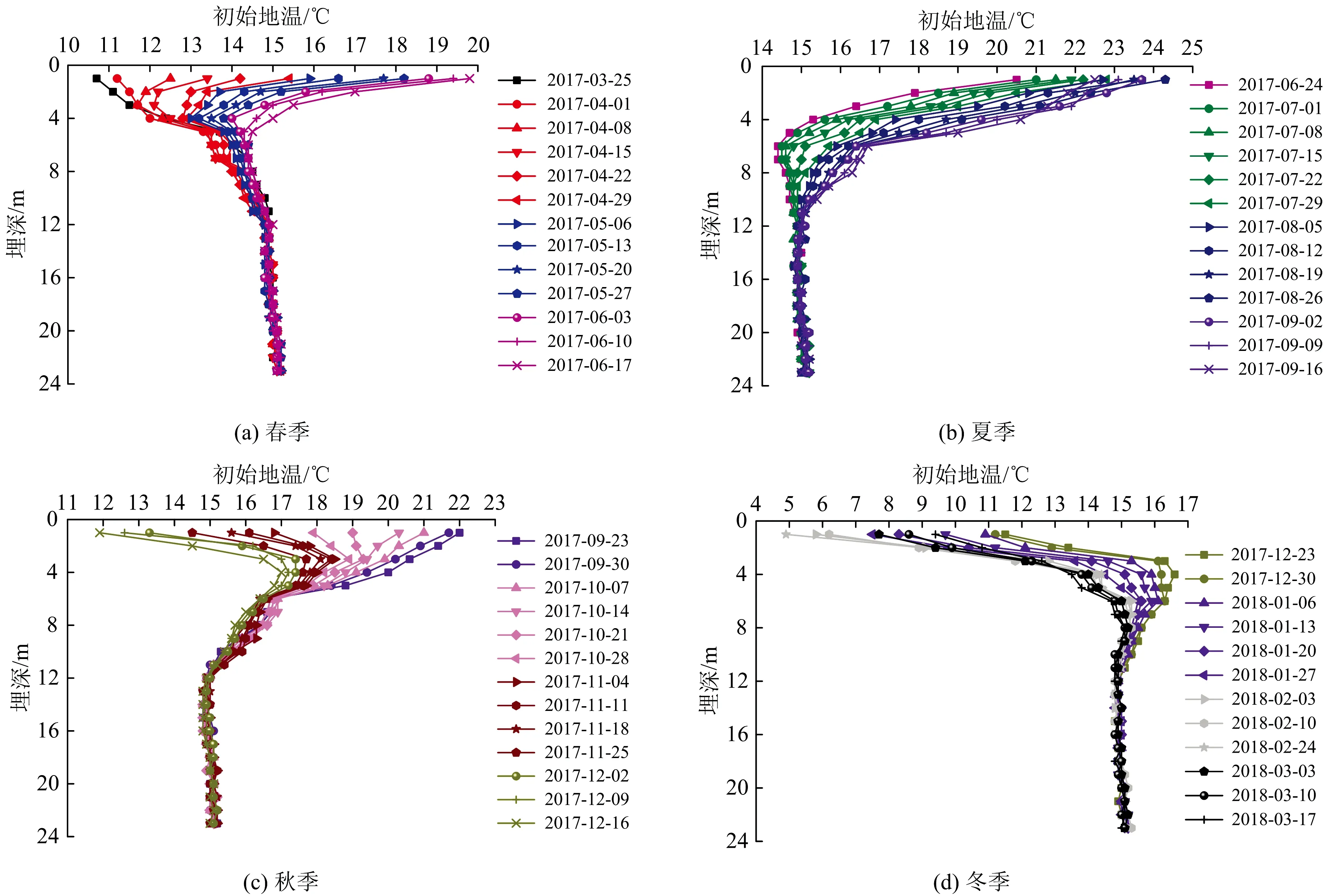
圖5 蘭州地鐵初始地溫隨埋深的變化規律

1) 初始地溫與環境氣溫的關系

地表至埋深5 m段內，初始地溫受環境氣溫的影響較為明顯，隨著環境氣溫的變化而發生變化。埋深5 m至埋深12 m段內，初始地溫受環境氣溫的影響相對于前一范圍更不明顯。埋深12 m至埋深23 m段內，初始地溫受環境氣溫的影響最小，在整個時節中隨時間的變化幅度小于0.3 ℃。可見，埋深越大，初始地溫受環境氣溫影響越小。

埋深1 m處的初始地溫：在春季，從10.8 ℃增大到19.8 ℃，增幅超過9 ℃；在秋季，減幅超過10 ℃，從22 ℃一直下降到11.9 ℃；在冬季，變幅超過5 ℃，最高可達11.5 ℃，最低可達4.9 ℃。每1個測點的初始地溫在各個時節中變化幅度均超過4 ℃。

2) 初始地溫與埋深的關系

地表至埋深12 m段內，隨埋深的增大，春季中，3月25日和4月1日的初始地溫都呈增大的趨勢，4月8日至6月17日的初始地溫都呈先減小后增大的趨勢；夏季中，6月24日至7月15日的初始地溫都呈先減小后增大的趨勢，7月22日至9月16日的初始地溫都呈減小的趨勢；秋季中，9月23日至10月14日的初始地溫都呈減小的趨勢，10月21日至12月16日的初始地溫都呈先增大后減小的趨勢；冬季中，初始地溫都呈先增大后減小的趨勢的趨勢。

埋深12 m至埋深23 m段內，隨埋深的增大，4季中初始地溫的變化幅度均較小，春季和夏季小于0.3 ℃，秋季和冬季小于0.4 ℃。

3)初始地溫平均值的分布規律

初始地溫平均值隨埋深的變化規律如圖6所示。由圖可知：地表至埋深12 m段內，隨埋深的增大，春季初始地溫平均值呈先增大后減小的趨勢，夏季初始地溫平均值呈減小的趨勢，秋季初始地溫平均值呈先增大后減小的趨勢，冬季初始地溫平均值呈增大的趨勢，全年初始地溫平均值呈先增大后減小的趨勢；埋深12 m至埋深23 m段內，隨埋深的增大，春、夏、秋、冬和全年初始地溫平均值的變化幅度均較小，小于0.4 ℃。

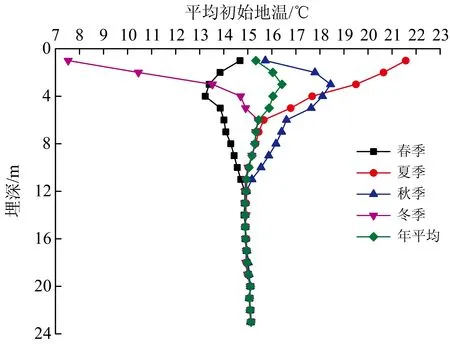
圖6 蘭州地鐵初始地溫平均值隨埋深的變化規律

地表至埋深3 m段內，初始地溫平均值從大到小的順序是夏季、秋季、全年、春季、冬季。埋深3 m至埋深12 m段內，初始地溫平均值從大到小的順序是秋季、夏季、全年、冬季、春季。埋深12 m至埋深23 m段內，春、夏、秋、冬和全年初始地溫平均值均在15 ℃左右。

由此可知，蘭州地鐵地層的初始地溫，年變溫層為地表至埋深12 m(不包含12 m)；年恒溫層為埋深12 m及其以下，溫度為15 ℃。

2.3 年變溫層中初始地溫分布規律

年變溫層中，埋深1，2，…，11 m處初始地溫的時程曲線如圖7所示。圖中橫坐標軸時間的1表示2017年3月21日，即春季的第1天，之后依次累加；本研究第1次溫度監測日期是2017-03-25，為第5天，其他監測日期的表達方式類似。從圖7可以看出，在初始地溫的年變溫層中，各埋深處的初始地溫年變化規律與環境氣溫變化規律相似，近似呈正弦曲線狀分布。

根據圖7每1個測點初始地溫的最大值和最小值，計算差值得到振幅，初始地溫的振幅隨埋深的變化規律如圖8所示。由圖8可知：1年中初始地溫的振幅隨埋深的增大逐漸減小。埋深為1 m時，1年中初始地溫的振幅大于18 ℃；埋深為11 m時，1年中初始地溫的振幅小于1 ℃。初始地溫的振幅與埋深呈指數關系。

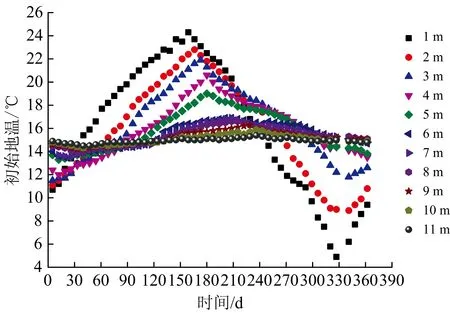
圖7 蘭州地鐵年變溫層中不同埋深的初始地溫時程曲線

圖8 蘭州地鐵初始地溫振幅隨埋深的變化規律

結合圖7和圖4可知：隨埋深的增大，1年中初始地溫的變化曲線存在初始地溫滯后于環境氣溫的現象，則環境氣溫對初始地溫的影響不是即時的而是有一定的滯后性。埋深1 m處，1年中初始地溫最高時日期是8月26日；隨著埋深逐漸增大，1年中初始地溫最高時日期逐漸往后推；到了埋深11 m處，初始地溫最高時日期是11月11日。1年中初始地溫最低時日期的變化規律與最高時相似。

3 初始地溫預測模型公式

以監測蘭州地鐵初始地溫的數據為基礎，提出蘭州地鐵初始地溫預測模型公式，以解析解的形式反映蘭州地鐵初始地溫。

3.1 地溫預測模型公式

3.1.1 變溫層

假定變溫層是均一介質，地層在深度方向的傳熱遠大于在水平方向的傳熱，基于傅里葉定律，可以得到一維傳熱方程表示的變溫層地溫[17]為

(1)

式中：T(z,t)為第t天深度z處的地溫， ℃；z為埋深，m；t為距離起算日期的時間，d；K為導熱系數，W·(m·K)-1。

地表處的地溫為[17]

T(0,t)=D0+A0sin(2πft+β)

(2)

式中：D0為地表處平均地下， ℃；A0為地表處地溫年變化幅值， ℃；f為頻率，1年365天，即可取1/365；β為初相角。

基于式(1)和式(2)，可求解得[17]

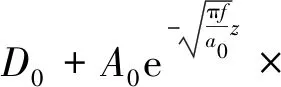
(3)

式中：a0為地表處的導溫系數，m2·d-1。

然而，蘭州地鐵的變溫層并不是同一介質，而是由多種介質構成的，不同介質的D，A，a均不相同，因此需對式(3)進行改進。對于同一介質的地層，地溫Ts(z,t)為

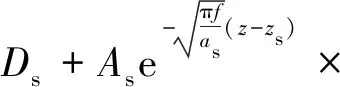
(4)

式中：Ds為同一介質地層的頂面處平均地溫， ℃；As為同一介質地層的頂面處地溫年變化幅值， ℃；as為同一介質地層的導溫系數，m2·d-1；zs為同一介質地層的頂面處深度，m；ts為同一介質地層中距離起算日期的時間，d。

3.1.2 恒溫層

在恒溫層中，地溫保持不變，設恒溫層的地溫為Th(℃)，則地溫可表示為

T(z,t)=Th

(5)

3.2 蘭州地鐵初始地溫預測模型公式的構建與驗證

3.2.1 變溫層

在初始地溫中，蘭州地鐵年變溫層自上而下依次由雜填土、素填土、黃土狀粉土、粉質黏土、粉細砂等組成，共5種介質。在鉆孔時對5種介質的地層分別取樣，并采用Hot Disk TPS2500s熱常數分析儀測試其熱物理參數，可得5種介質地層的as；根據每個測點的年平均初始地溫，按照相對的范圍對其進行線性內插可得各個介質地層的Ds，其中地表年平均初始地溫，與恒溫層初始地溫相等[18]，為15.00 ℃；各介質地層的As通過圖8的擬合函數可得；各介質地層的βs通過該層的任意1個溫度監測數據(圖8的坐標點)便可確定；由此得到各介質地層Ds，As，as，βs參數的取值見表1。

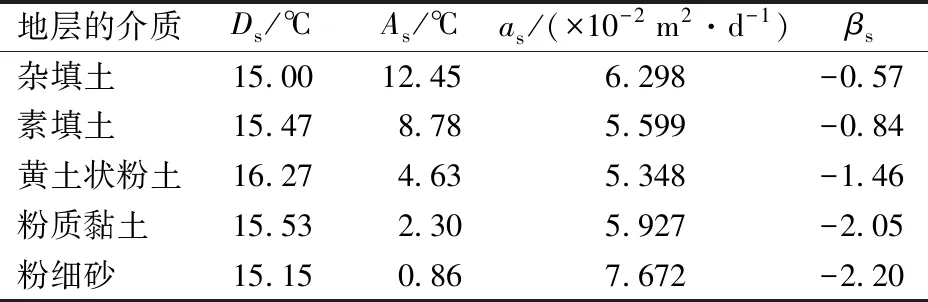
表1 模型參數的取值

z取1，2，3，…，11，對應圖1的地層范圍確定地層的介質，根據地層介質在表1中選取模型參數的值，代入式(4)，得到11個式子，這11個計算公式就是蘭州地鐵初始地溫預測模型公式，分別命名為式(6-1)、式(6-2)、式(6-3)，…，式(6-11)。采用該預測模型公式預測2017-03-25至2018-03-17的蘭州地鐵初始低溫地溫時程曲線，如圖9所示。對11條曲線分別進行擬合，其R2都大于0.85，說明采用該模型可以較為準確地預測蘭州地鐵初始地溫預測。

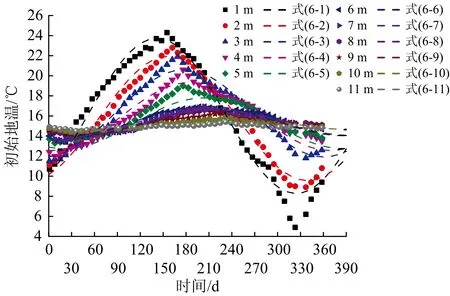
圖9 預測的蘭州地鐵變溫層中不同埋深的初始地溫時程曲線

3.2.2 恒溫層

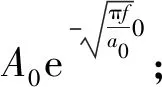
(7)

根據式(7)可求得

(9)

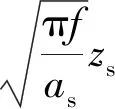
4 運營條件下蘭州地鐵隧道圍巖溫度演化規律

根據蘭州地鐵初始地溫的監測數據和預測模型公式，再運用非穩態傳熱的數值模型，模擬計算蘭州地鐵運營過程中隧道內空氣與圍巖之間熱交換形成的圍巖溫度，探究地鐵運營條件下圍巖溫度的演化規律。

4.1 圍巖溫度非穩態傳熱數值模型的建立

4.1.1 控制方程

熱存儲項的計入將穩態系統轉變為非穩態系統，非穩態傳熱分析的控制方程為[19]

(10)

式中：C為比熱容矩陣；T為圍巖溫度或者隧道內環境溫度向量；K為導熱系數矩陣；Q為熱流率向量。

在非穩態傳熱分析中，熱流率隨時間變化時，非穩態傳熱分析的控制方程為[19]

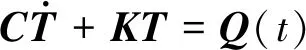
(11)

采用有限元分析軟件Ansys，對方程式(11)求解，得到隧道內不同環境溫度時的地鐵隧道的圍巖溫度。

4.1.2 隧道模型

地鐵隧道底板埋深設計是19.5～21.8 m，且周圍土體為卵石土。設置隧道模型均處于恒溫層中，整個隧道模型的初始圍巖溫度為15 ℃，隧道模型的上下邊界與左右邊界條件均一致。參考蘭州地鐵隧道設計尺寸，將模型中的地鐵隧道斷面設為圓形，半徑為2.7 m，襯砌厚0.6 m，與圍巖直接接觸。隧道模型圓心為點(0, 0)，設圓心距離隧道模型頂面(恒溫層底面)為8 m，圓心距離隧道模型底面為27 m，圓心距離隧道模型左面和右面都為27 m。隧道模型單元的邊長為0.1 m。

4.1.3 圍巖溫度非穩態傳熱數值模型的地層介質物理參數

采用Hot Disk TPS2500s熱常數分析儀測試蘭州地鐵卵石土和混凝土襯砌的熱物理參數，結果見表2。圍巖溫度演化過程主要靠隧道內空氣與襯砌圍巖之間產生的對流進行熱交換，隧道壁面的換熱系數為10.0 W·(m2· ℃)-1 [20]。

表2 圍巖與支撐結構的熱物性參數

4.1.4 圍巖溫度非穩態傳熱數值模型的模擬工況

地鐵圍巖溫度演化過程主要考慮的影響因素有：地鐵運營時長，隧道內環境溫度、圍巖初始溫度、圍巖及襯砌的熱物理參數。其中，圍巖初始溫度、圍巖及襯砌的熱物理參數均已確定。

根據《地鐵設計規范》[21]，在空調調控中，地鐵隧道內環境溫度最高不應高于30 ℃，最低應等于當地地層的自然溫度，同時最低不應低于12 ℃。因此，設定隧道內環境溫度分別為20，25和30 ℃(沒有考慮通風風速)，探究隧道內不同環境溫度時隨著地鐵建成時間的增加地鐵隧道圍巖溫度的演化規律。

4.2 數值模型有效性驗證

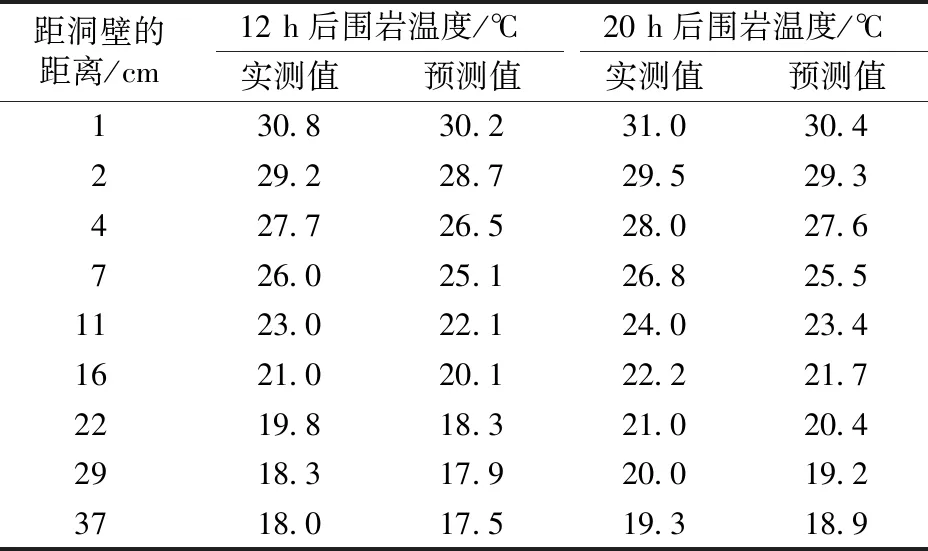
以胡增輝的地鐵隧道模型試驗參數[11]為基礎，運用Ansys及控制方程[19]，建立胡增輝的地鐵隧道模型的數值模型，初始圍巖溫度取15.8 ℃，隧道內溫度取地鐵設計的隧道內環境極限溫度35 ℃。采用胡增輝地鐵隧道模型試驗得到的距洞壁不同距離處不同熱交換時間時圍巖溫度的實測值[11]與采用本文預測方法得到的預測值進行對比，見表3。從表3中可以看出，預測值在實測值的5%誤差以內，誤差較小，驗證了本文預測方法的合理性和有效性。

4.3 數值模擬結果及分析

4.3.1 圍巖溫度分布云圖

隨著地鐵建成時間的增加隧道圍巖溫度分布云圖如圖10所示。由圖可知：隧道內空氣與圍巖之間熱交換1個月后，隧道圍巖溫度等溫線以同心圓形態分布，圍巖溫度大于16 ℃的面積不到數值模型總面積的1/10；熱交換6個月后，隧道圍巖有一部分溫度等溫線分布形態開始呈扁圓形；熱交換5年后，等溫線基本呈扁圓形，圍巖溫度大于16 ℃的面積約是數值模型總面積的1/2；隨距隧道內壁距離的增大，圍巖溫度等溫線間距呈增大的趨勢，說明距離隧道內壁越遠，圍巖溫度梯度越小，圍巖溫度變化幅度相對更小。

表3 距洞壁不同距離處不同熱交換時間時圍巖溫度的實測值與預測值對比

距洞壁的距離/cm12 h后圍巖溫度/℃20 h后圍巖溫度/℃實測值預測值實測值預測值130.830.231.030.4229.228.729.529.3427.726.528.027.6726.025.126.825.51123.022.124.023.41621.020.122.221.72219.818.321.020.42918.317.920.019.23718.017.519.318.9

圖10 隧道圍巖溫度分布云圖(單位：℃)

4.3.2 隧道內環境溫度對圍巖溫度分布的影響

取自隧道拱頂向上至數值模型邊界的線為A線，自隧道右側壁且坐標y=0處向右至數值模型邊界的線為B線，自隧道仰拱中點向下至數值模型邊界的線為C線。

3條線上隧道圍巖溫度的分布規律如圖11所示。由圖可知：圍巖溫度與距隧道內壁距離成負相關關系；以C線的溫度為例，隧道內環境溫度相同時，隨熱交換時間的延長，同一位置處的溫度逐漸增大，圖中曲線的斜率逐漸增大，即溫度梯度呈增大的趨勢；熱交換時間相同時，隨隧道內環境溫度的增大，同一位置處的溫度逐漸增大，溫度梯度呈增大的趨勢；對于A線和B線，溫度及溫度梯度隨熱交換時間或隧道內環境溫度的變化規律類似。

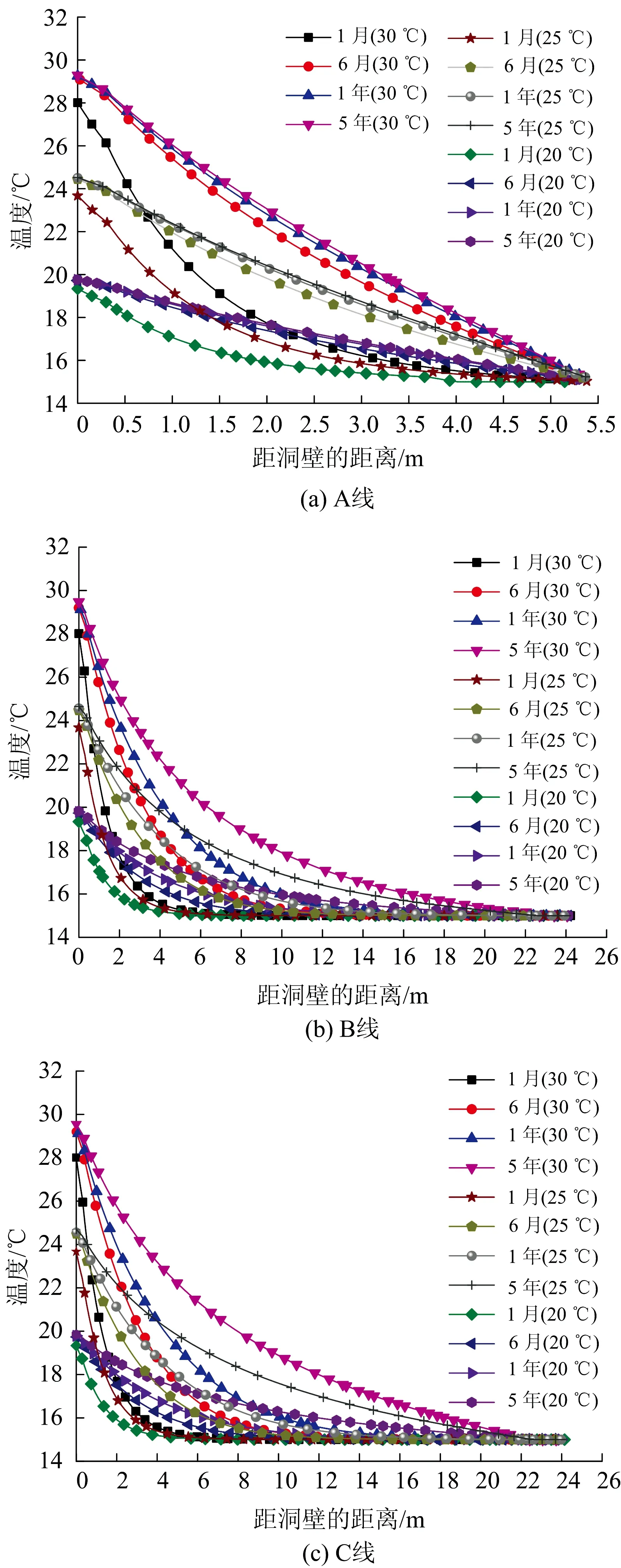
圖11 隧道圍巖溫度的分布規律

分析圖10，隧道各處的圍巖溫度及圍巖溫度梯度分布情況與A線、B線、C線類似。因此，圍巖溫度及溫度梯度與隧道內環境溫度、熱交換時間均成正相關關系。

熱透厚度指隧道內壁與圍巖溫度穩定處的距離。定義圍巖溫度變化小于5%處為圍巖溫度穩定處[11]。以C線為例，熱透厚度見表4。由表4可知：隧道內環境溫度相同時，隨熱交換時間的延長，熱透厚度逐漸增大；熱交換時間相同時，隨隧道內環境溫度的增大，熱透厚度逐漸增大，但是增大幅度呈減少的趨勢；熱交換時間相同的情況下，隧道內環境溫度為30 ℃的熱透厚度與隧道內環境溫度為25 ℃的熱透厚度相差不到0.5 m；對于A線和B線，熱透厚度隨熱交換時間或隧道內環境溫度的變化規律類似；結合圖10的圍巖溫度分布云圖，熱透厚度未達到極限(數值模型邊界處溫度變化為5%)時，熱透厚度與隧道內環境溫度成正相關關系，與熱交換時間時間成正相關關系。

表4 不同隧道內環境溫度時不同熱交換時間下的隧道圍巖熱透厚度(C線)

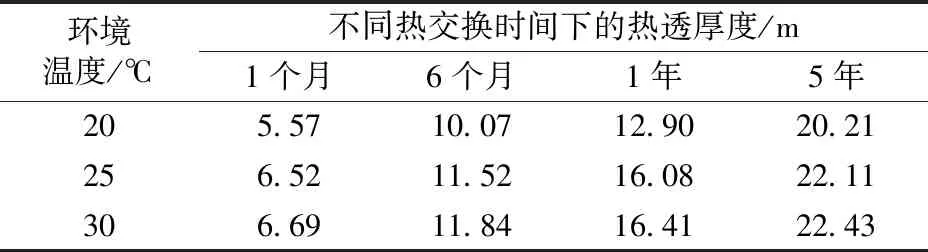
環境溫度/℃不同熱交換時間下的熱透厚度/m1個月6個月1年5年205.5710.0712.9020.21256.5211.5216.0822.11306.6911.8416.4122.43

5 結 論

(1)蘭州地鐵初始地溫，隨著環境氣溫的不同而不同，隨著埋深的不同，其變化規律不同；年變溫層位于自地表至埋深12 m處；年恒溫層位于埋深12 m以下，溫度為15 ℃左右。

(2)年變溫層中，1年內初始地溫變化規律與環境氣溫變化規律相似，近似呈正弦曲線狀分布，但存在相位滯后的現象；1年中初始地溫的振幅隨埋深的增大呈指數減小。

(3) 基于實測數據，提出蘭州地鐵初始地溫預測模型公式，以解析解的形式反映蘭州地鐵初始地溫。

(4) 在隧道內空氣與圍巖之間熱交換過程中，蘭州地鐵隧道圍巖溫度、圍巖溫度梯度與隧道內環境溫度、熱交換時間均成正相關關系，與隧道內壁距離成負相關關系。

(5) 在隧道內空氣與圍巖之間熱交換過程中，熱透厚度未達到極限(數值模型邊界處溫度變化為5%)時，熱透厚度與隧道內環境溫度、熱交換時間均成正相關關系。