基于偶次諧波吸收率函數復現方法

周佩麗,譚 文,彭志敏

(1.華北電力大學控制與計算機工程學院,北京 102206;2.清華大學能源與動力工程系,北京 100084)

1 引 言

可調諧二極管激光吸收光譜(tunable diode laser absorption spectroscopy,TDLAS)由于波長選擇性好、靈敏度高、非接觸測量等優點得到快速發展[1-4],其中,吸收率函數是TDLAS的核心函數,蘊含了氣體溫度、壓力、濃度和譜線光譜常數等信息[5-7],但目前吸收率函數一般只能通過直接吸收光譜(direct absorption spectroscopy,DAS)測量得到,直接吸收法雖然物理概念清晰,操作簡單,但在測量中容易受到顆粒物濃度、激光強度波動、基線擬合不確定性等因素影響,進而導致較大的測量誤差[8-9]。

為了提高TDLAS的測量精度和靈敏度,解決惡劣環境以及弱吸收條件下氣體溫度、濃度等參數的測量難題,科研工作者將波長調制思想引入到TDLAS中[10]。波長調制光譜(wavelength modulation spectroscopy,WMS)在測量過程中通過對目標信號進行高頻調制,而非目標信號由于沒有經過調制在后續的諧波檢測過程中被除去,因此可以有效地降低測量系統中噪聲信號干擾。但傳統波長調制光譜一般需要通過二次諧波峰值和復雜的標定實驗來確定待測氣體濃度等參數[11],而標定實驗制約了波長調制光譜的廣泛應用。為了解決波長調制光譜需要標定的難題,自2006年以來,R.K.Hanson課題組基于剩余幅度調制提出了2f/1f免標法,該方法采用一次諧波信號來修正二次諧波,不僅消除了激光強度波動、光電放大系數等因素的影響,并在此基礎上推導出了確定氣體溫度和濃度的表達式。2f/1f免標法并不是通過測量吸收率函數來確定待測氣體參數,而是通過比較諧波信號的理論計算與實驗測量值來獲得[12],但在實際測量中,諧波信號不僅與氣體溫度、壓力、組分濃度等參數有關,而且與激光光強調制、頻率調制以及光強調制與頻率調制相位差等參數有關,上述參數的不確定性往往使得諧波信號的理論計算值偏離真實值,進而導致氣體參數的測量誤差。

考慮到吸收率函數的重要性(可直接確定待測氣體溫度、濃度以及分子光譜常數等)以及波長調制光譜的優點(抗干擾能力強、信噪比高等),近年來,科研工作者嘗試利用高信噪比的諧波信號復現TDLAS的核心參數——吸收率函數。其中具有代表性的工作有:G.Stewart等在研究中發現當調制系數很小時,一次諧波X或Y軸分量與吸收率函數相似,可實現吸收率函數的近似測量,但其測量誤差會隨著調制系數的增大而急劇增大[13-16]。藍麗娟等利用數值模擬獲得譜線中心頻率處二次與四次諧波比值與線型函數之間的關系,利用不同線型函數在同一調制系數下交于同一固定點的特征實現線型函數的測量,然后利用調制系數為0.94時二次諧波與一次諧波比值和吸收率函數之間的關系實現峰值吸收率的測量,進而得到完整的吸收率函數信息,但該方法一般只適用于單譜線和弱吸收條件下線型函數和峰值吸收率的測量[17-19]。在之前的研究中,我們利用剩余調制幅度采用奇次諧波對吸收率函數進行復現,該復現過程測量精度與激光頻率調制和光強幅度調制之間的相位差有關,相位差越大,測量精度越高,而在實際測量中若想得到較大的相位差需要極高調制頻率[20]。

基于上述研究可發現,波長調制光譜中各次諧波均蘊含了吸收率函數信息。本文通過對高頻調制后的激光透過率函數進行泰勒級數分析建立了諧波信號與透過率之間的關系,并在此基礎上提出了一種基于偶次諧波的吸收率函數復現方法,同時以CO2分子6976.203 cm-1譜線為例進行了數值模擬和實驗驗證。

2 理論推導

在波長調制光譜中,中心頻率為v0的激光經過頻率為ω的高頻正弦信號調制后,激光瞬時頻率v表達式為:

ν=ν0+acos(ωt+φ)

(1)

式中,a(cm-1)為頻率調制幅度;φ為激光頻率調制的初始相位角;定義調制系數:m=a/γ,其中γ為譜線半高半寬。

根據Beer-Lambert定律可知,激光透射光強It與入射光強I0的比值即激光透過率τ(v)表達式如下:

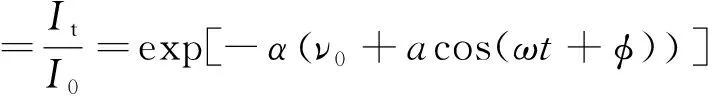
(2)

式中,α(ν0+acos(ωt+φ))為激光吸收率,Hk為激光透過率函數的各次諧波分量,其表達式為:

(3)

將激光透過率τ(ν0+acosθ)在譜線中心頻率v0處進行泰勒級數展開可得到:

(4)

將公式(4)代入公式(3),可得偶次諧波展開式各項如下式:

(5)

通過分析公式(5)可以發現:零次諧波H0與二次諧波H2相減可以將無法求解的τ(2)(ν0)a2項消除,同理,零次諧波H0與二次諧波H2相減然后與四次諧波H4相加后可將無法求解的τ(4)(ν0)a4項消除。以此類推,偶次諧波間的關系特征可用下式描述:

(6)

當k趨近于無窮大時,高階項為零,即滿足:

τ(ν0)=exp[-α(ν0)]=funk|k→∞

(7)

將funk代入下式,即得到氣體吸收率α(ν0)為:

α(ν0)=-ln(funk)|k→∞

(8)

3 數值模擬

數值模擬以CO2分子6976.203 cm-1譜線為例,其譜線參數如表1所示。

表1 CO2氣體6976.203 cm-1譜線參數(296 K)

模擬計算條件為:光程L為52.5 cm,CO2濃度X為100 %,溫度T為296 K,壓力P為0.5atm,在該條件下,譜線半高半寬為0.0593 cm-1,假設調制系數m分別為1.0和2.0,將以上各參數代入公式(2)和(3)中計算得到激光透過率函數的0次、2次、4次、6次諧波及根據該方法復現得到的吸收率函數分別如圖1(a)和圖1(b)所示。

圖1數值模擬結果證明本文提出的偶次諧波可以實現吸收率函數復現,該方法具有以下特征:①圖1(a)和(b)共同顯示fun3(0、2、4、6次諧波)復現結果比fun1(0、2次諧波)復現結果更接近真實吸收率,即隨著所采用諧波階次的增加,偶次諧波復現吸收率函數精度越高；②對比圖1(a)和(b)吸收率函數復現結果,當調制系數為1.0時,使用fun2(0、2、4次諧波)對吸收率進行重構便可實現較高測量精度,而當調制系數為2.0時,采用fun3(0、2、4、6次諧波)對吸收率函數進行重構也會存在誤差,但此時誤差小于2 %,即隨著調制系數的增大,復現吸收率函數需要使用的諧波階次越高。

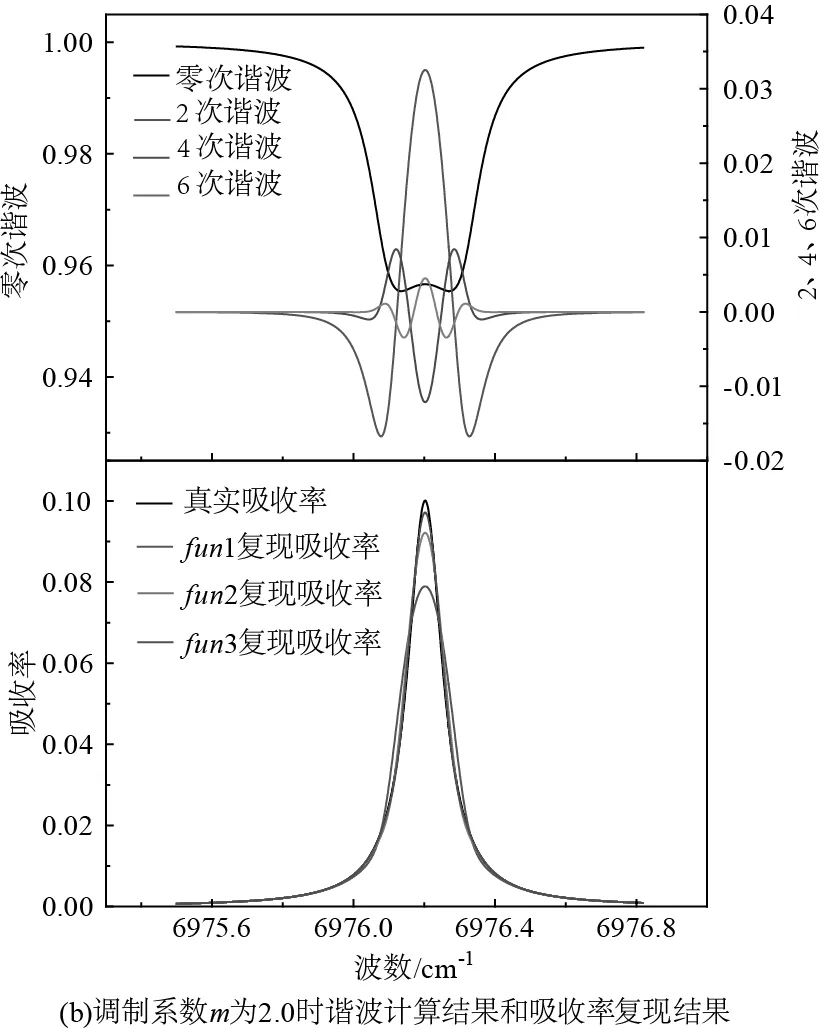
圖1 偶次諧波復現吸收率函數數值模擬結果

4 實驗驗證

4.1 實驗方案

實驗方案如圖2所示,信號發生器(KEYSIGHT 33500B Series)產生的10 kHz高頻正弦信號與激光控制器ITC4001內部產生的低頻三角波信號(20 Hz)疊加后共同驅動激光二極管(NEL,型號NLK1E5EAAA)產生特定頻率的激光,并在該頻率處實現低頻掃描和高頻調制。輸出激光經過光纖分束器(分束比例1∶2∶2)后分成三束,20 %激光光束準直(Thorlabs F280FC-1550)后經過F-P干涉儀(Thorlabs SA200-15C,自由光譜區為0.05 cm-1)產生干涉信號由光電探測器(Thorlabs PDA50B)接收,第二束激光準直后射入待測氣室產生透射光強信號由光電探測器接收,另一束作為參考信號。

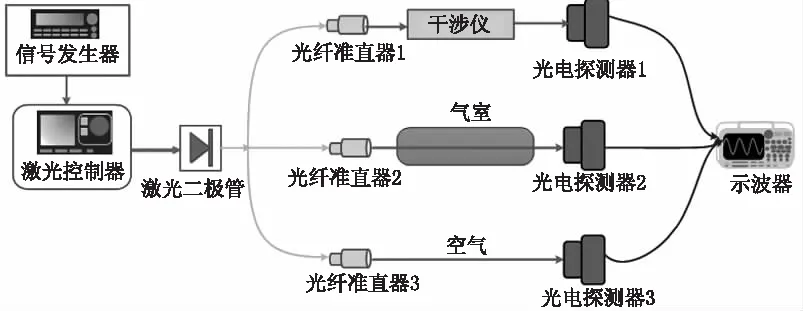
圖2 偶次諧波復現吸收率函數實驗方案

數據處理采用LabVIEW實現,數據處理過程如圖3所示,該過程包括兩部分:激光參數標定和吸收率函數復現。激光參數標定時,對經過10 kHz高頻正弦波調制后的激光形成的干涉信號進行正弦擬合,可得到激光在該調制頻率下的電流調諧系數(cm-1/mA)。吸收率函數復現時,首先根據Beer-Lambert定律對氣體吸收信號It和參考信號I0得到激光透過率τ(t),然后對激光透過率τ(t)進行低通濾波后得到零次諧波H0,同時對激光透過率函數τ(t)進行鎖相檢測得到2、4、6次諧波H2、H4、H6,最后將上述過程得到的各次諧波代入公式(6)和(8)即可實現吸收率函數復現。

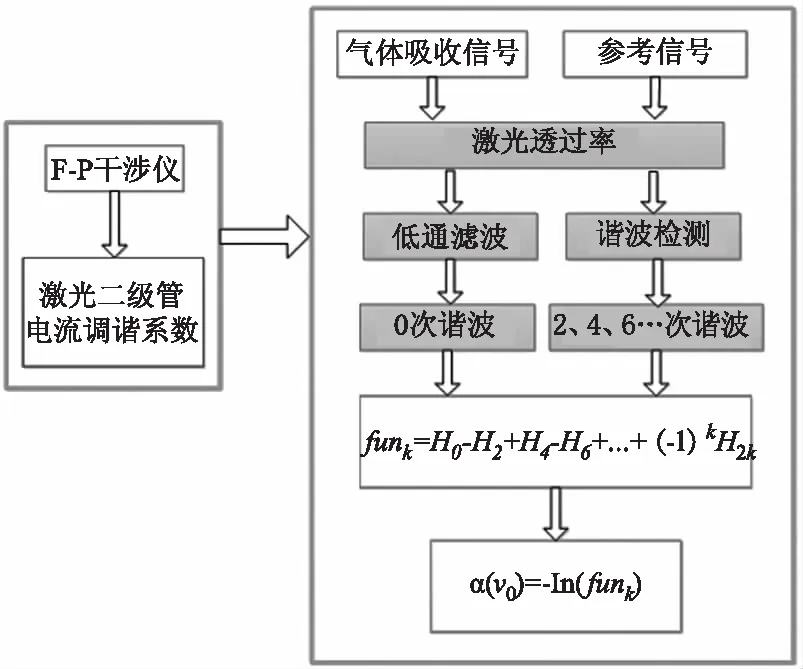
圖3 基于偶次諧波的吸收率函數復現數據處理流程

4.2 實驗結果

4.2.1 電流調諧系數標定

激光控制器驅動激光二極管發出6976.203 cm-1波長激光時對應的溫度和電流分別為29.44 ℃、70 mA,此時加載10 kHz正弦信號使激光二極管在譜線中心頻率處產生高頻調制,調制電流峰值為20 mA,此時光強信號和經過干涉儀得到的干涉信號如圖4所示。

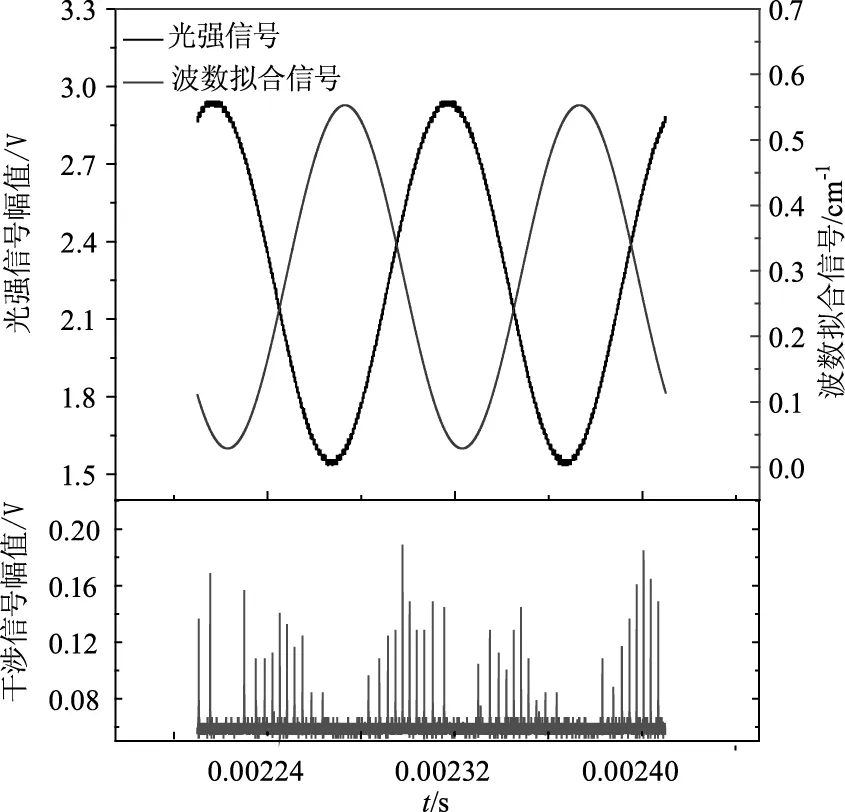
圖4 激光二極管電流調諧系數標定

電流調諧系數標定時,首先確定各干涉峰值處對應的時間值,然后根據該干涉儀的自由光譜區(0.05 cm-1)對各干涉峰的相對波數進行編號,得到波數-時間數列,最后按照公式(1)對該數列進行正弦擬合,得到頻率調制幅度a為0.262 cm-1,從而確定該激光二極管此時對應的電流調諧系數為0.0131 cm-1/mA。

4.2.2 吸收率函數復現結果

在室溫(297 K)條件下,向待測氣室內充入濃度X為100 %、壓力P為26.7 kPa的CO2氣體,該條件下譜線半高半寬γ為0.0322 cm-1,在高頻正弦波信號(3.5 mA/10 kHz,調制系數m約為1.42)和低頻三角波掃描信號(15 mA/20 Hz)共同調制下氣體吸收信號It和原始光強信號I0及激光透過率τ(t)如圖5(a)所示,經過低通濾波得到的零次諧波和經過鎖相檢測得到的2、4、6次諧波如圖5(b)所示。

將上述過程中得到的各次諧波H0、H2、H4和H6代入公式(6)和(8)計算得到吸收率函數如圖6所示,圖中展示了傳統直接吸收法測量結果,由下至上曲線依次為fun1、fun2、fun3復現結果。由該圖可以看出,采用fun1(0、2次諧波)復現時,由于采用諧波階次較低,激光透過率和調制幅度等組成的高階項影響較大,吸收率函數復現結果與直接吸收法存在較大誤差,而采用fun2(0、2、4次諧波)和fun3(0、2、4、6次諧波)復現時,由于采用的諧波階次增高,吸收率復現結果與直接吸收法誤差變小,尤其是采用fun3的吸收率復現結果與直接吸收法測量結果一致。

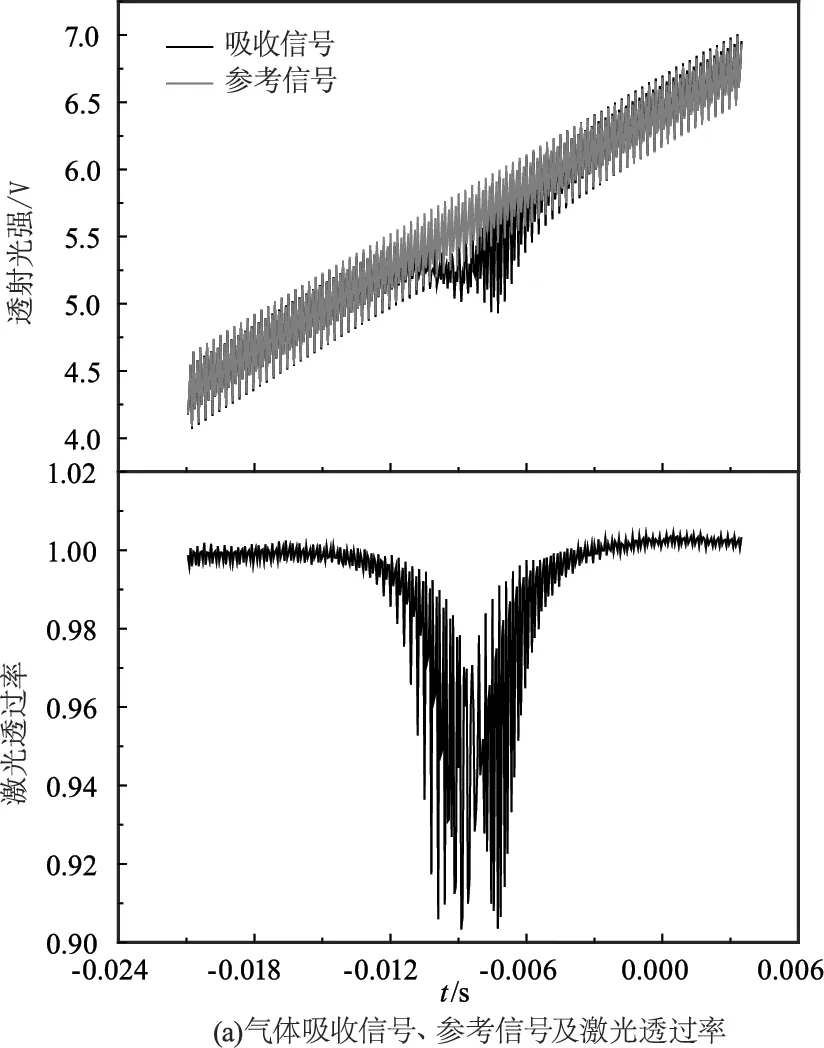
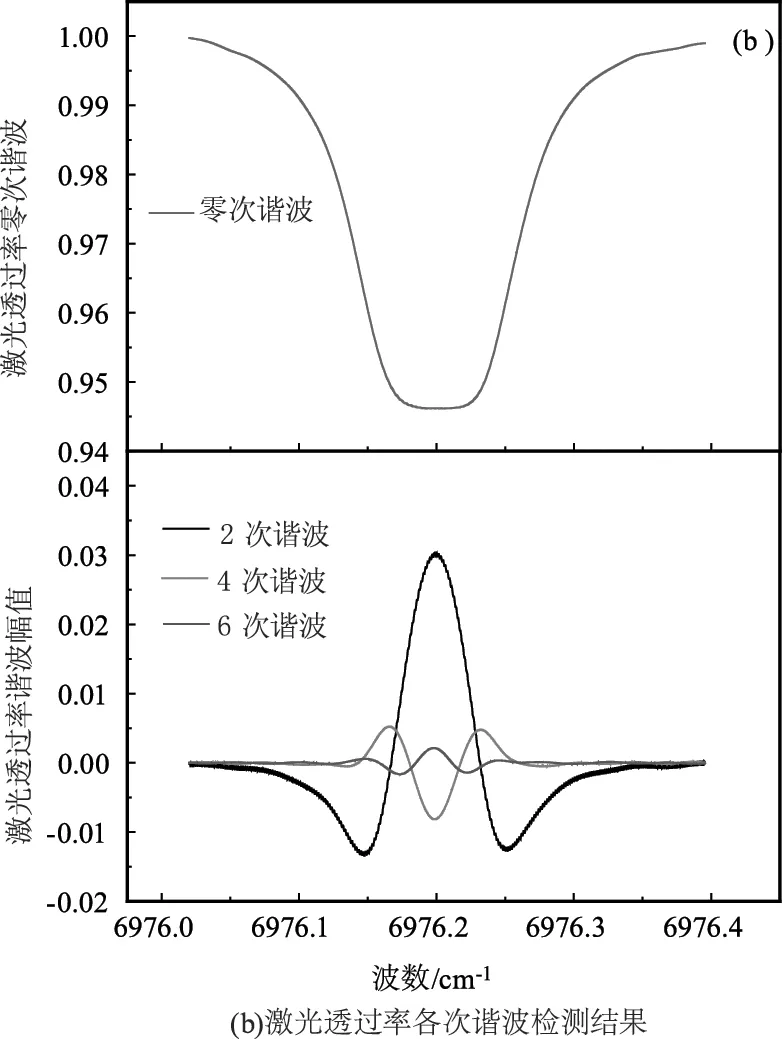
圖5 3.5 mA、10 kHz正弦調制信號實驗結果

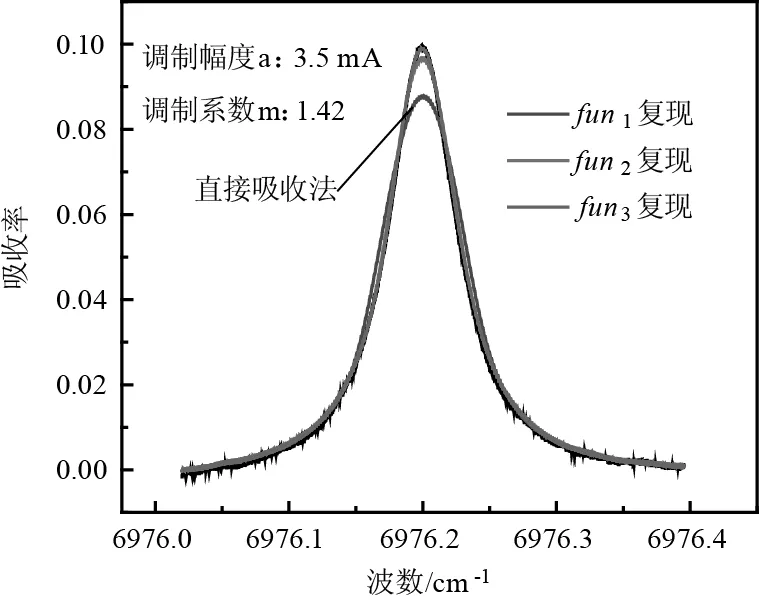
圖6 偶次諧波復現吸收率函數實驗結果(3.5 mA/10 kHz)

該方法理論推導和數值模擬過程顯示各偶次諧波中均蘊含著吸收率函數信息,而偶次諧波幅值與頻率調制幅度有關,隨著頻率調制幅度的增大,其對各次諧波中τ(2)(ν0)a2、τ(4)(ν0)a4等高階項影響越大,因此消除高階項影響需要的諧波階次越高。為了分析頻率調制幅度對該方法的影響,驗證實驗中采用多個調制幅度進行了對比,正弦調制信號頻率均為10 kHz,調制電流峰值分別為1.5 mA、2.5 mA和3.5 mA,對應的調制系數分別約為0.61、1.02和1.42。調制系數為1.42時的吸收率函數復現結果如圖6所示,調制系數0.61和1.02時對應的吸收率函數復現結果如圖7所示。

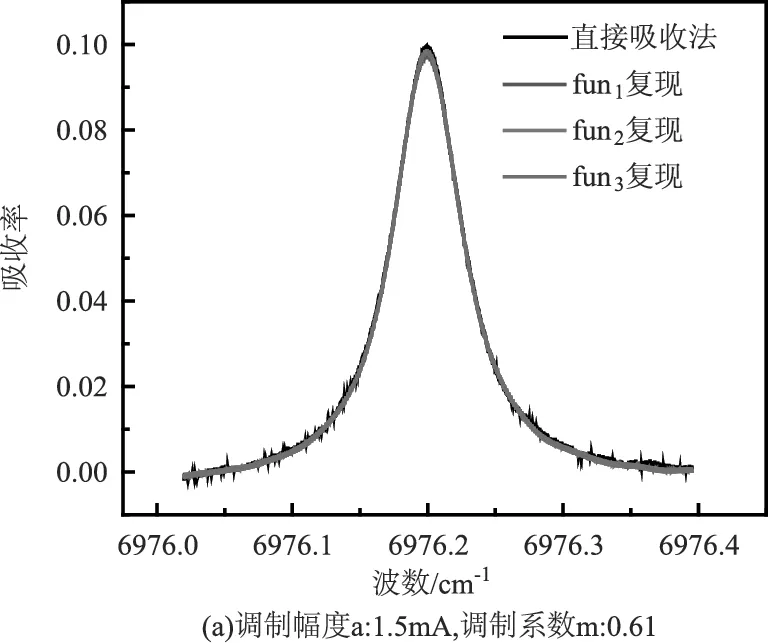
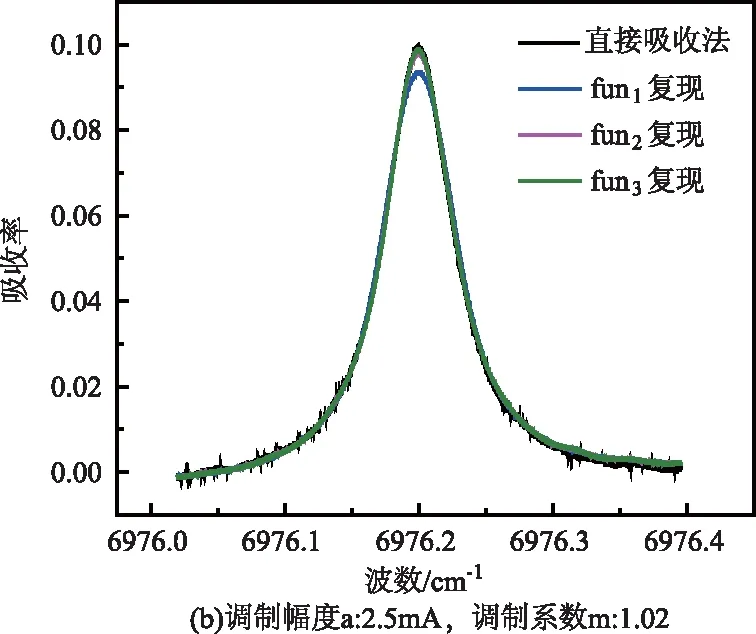
圖7 不同調制幅度下偶次諧波復現吸收率函數實驗結果

通過圖6和圖7對比可以看出,當調制系數為0.61時,采用fun1(0、2次)對吸收率函數進行復現便可得到與直接吸收法相近的結果,當調制系數為1.02時,采用fun1(0、2次)對吸收率函數復現時便存在較大誤差,采用fun2(0、2、4次)對吸收率函數復現時誤差減小,而當調制系數為1.42時,需要采用fun3(0、2、4、6次)復現才能實現與直接吸收法測量結果一致,即隨著調制系數的增大,采用該方法復現吸收率函數時所需要的諧波階次越高。

5 結 論

考慮到目前波長調制光譜尚無有效測量吸收率函數的理論和方法,本文基于波長調制光譜理論對經過高頻調制后的激光透過率函數進行泰勒級數展開,然后將泰勒級數展開式代入各次諧波分量中發現偶次諧波可通過運算消除高階項的影響,進而得到激光透過率函數,本文基于此建立了一種偶次諧波復現吸收率函數的理論和方法,并以CO2分子6976.203 cm-1處譜線為例進行了數值模擬和實驗驗證,同時將實驗結果與直接吸收光譜測得的吸收率函數進行了對比。數值模擬和實驗結果表明:該方法可以實現吸收率函數的高精度復現,且隨著采用諧波階次的增大,該方法測量精度越高。但該方法的應用與頻率調制幅度有關,即隨著頻率調制幅度的增加,消除高階項影響需要的諧波階次越高,從而復現吸收率函數時需要的諧波階次越高。而在波長調制光譜中,諧波檢測信噪比與調制系數有關,因此該方法的應用原則為在較高信噪比的調制幅度下選擇足夠的諧波階數對吸收率函數進行復現。本文建立了波長調制光譜與TDLAS核心參數—吸收率函數之間的關系,解決了傳統波長調制光譜應用中需要標定的問題,未來擬將其應用于譜線參數標定及復雜工業現場氣體參數測量中。