遺傳算法在更換APU渦輪葉片工藝中的應用

王冰 趙鑫 王璐璐

摘要：在飛機輔助動力裝置（APU）更換渦輪葉片工作中，由于葉片數量較多，盲目排序葉片容易造成不平衡量超標的情況，極大地影響了維修質量與效率。本文基于渦輪組件靜平衡質量模型，結合旅行商（TSP）問題的求解方法，提出一種基于精英保留策略的改進遺傳算法。該算法具有良好的收斂特性，將該算法應用于更換渦輪葉片工藝中，可提高渦輪的修理質量與效率。

關鍵詞：輔助動力裝置；渦輪葉片；遺傳算法

Keywords：APU；turbine blades；genetic algorithms

1 渦輪組件靜平衡分析

渦輪組件作為輔助動力裝置（APU）的核心動力部件，其結構組成主要包括渦輪盤、渦輪葉片以及鎖片、封嚴等（見圖1）。受生產制造過程中的材質不均、工藝誤差、渦輪葉片不均勻及運行過程中造成的局部磨損等因素的影響，渦輪組件上總是存在著不平衡狀態。由于APU運行過程中其核心機轉速將達到50000r/min，當不平衡狀態超出設計范圍時，將對軸承與機匣等結構造成不良影響。由于渦輪組件為薄盤型、不平衡量沿軸向分布所產生的力偶可忽略不計，且組件徑向剛度較大，運行轉速遠高于結構的固有頻率。結合APU生產廠家對于渦輪組件修理的要求，車間需對更換葉片的渦輪組件完成靜平衡測試工作，并要求靜不平衡量限制在維修手冊要求范圍之內，以保證修后渦輪組件的質量滿足運行要求。

靜不平衡即將不平衡力簡化為作用于質心的一個集中不平衡力，此時不平衡力為集中于質心的不平衡質量在旋轉作用下所產生的離心力。因此，對于靜不平衡的分析可簡化為在垂直于軸線的質心平面上分析質心偏離回轉中心的問題。

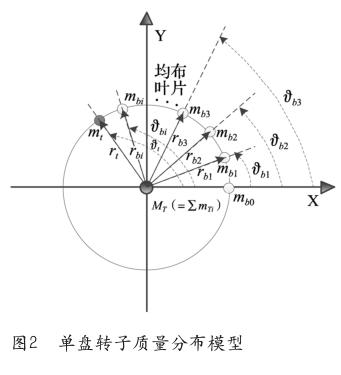
根據APU渦輪組件的結構特點，建立如圖2所示的單盤質量分布模型。其中，MT為去除不平衡量后的理想渦輪盤質量，MTi為組成理想渦輪盤的質量點的質量，Rti為渦輪盤質量點相對回轉中心的徑矢，mt為測得渦輪盤不平衡質量，θt為渦輪盤不平衡量角度，Rt為渦輪盤不平衡質量相對回轉中心的徑矢，mbi為葉片i的質量，rbi為葉片i質心相對回轉中心的徑矢。

由于APU渦輪組件由渦輪盤與葉片組裝而成，不平衡量可認為是由渦輪盤自身不平衡量與每個葉片的不平衡量共同組成。由質心定義及靜平衡定義可知，所求取葉片的最優排序問題可視作求解質心偏離回轉中心軸最小值問題。即：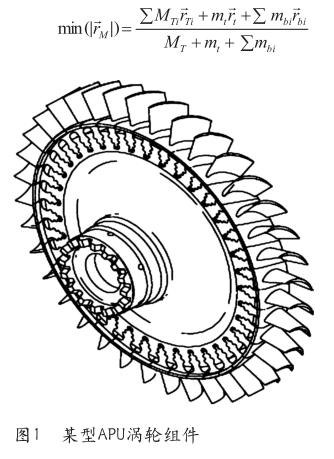

2 遺傳算法計算步驟

由于APU渦輪葉片數量較多，對其目標函數的最優值求解可視作大規模旅行商（TSP）模型的求解問題，對這類模型的求解目前僅有全排列方法可以獲得全局最優解，但其計算次數極大，以本文所述型號渦輪組件，安裝37枚葉片，計算次數將達到1.38×1043次（37！次），是一般的計算機所無法承受的計算量。對于這類模型，目前求解較為有效的計算方法主要包括遺傳算法、蟻群算法、神經網絡算法、模擬退火算法等智能優化算法。因此，針對本文所面對的渦輪葉片排序問題的特點，在其模型編碼與程序實現工作中采用遺傳算法相比其他算法更加簡便，且在全局尋優性能上也足以滿足計算要求。

遺傳算法是模擬達爾文生物進化論的自然選擇和遺傳學機理的生物進化過程的計算模型，是一種通過模擬自然進化過程搜索最優解的方法。該算法從代表問題可能潛在的一個種群（解集）開始，通過對種群中每一個解（染色體）的內部構成（基因）在適應性（適應度函數）的引導下，不斷進行篩選組合并生成更優質染色體，最終獲得目標解。

遺傳算法在處理全局尋優時計算效率很高，但對于TSP排列組合模型，傳統的遺傳算法容易造成“退化”情況，即新生最優染色體的適應度低于父級最優染色體的適應度。因此，在選擇種群時采用結合精英保留策略的錦標賽篩選法，以求取最優的排列組合。

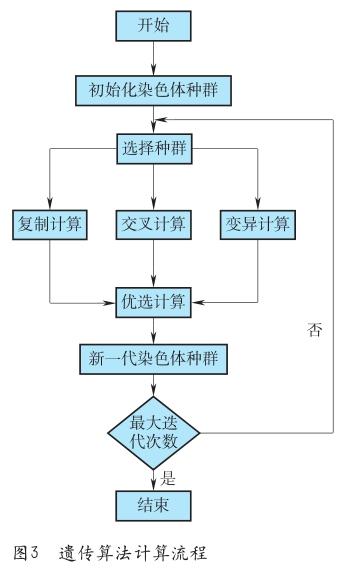
葉片排序的主要步驟包括產生初始染色體種群、計算個體適應度函數、選擇種群、復制計算、交叉計算、變異計算、優選計算、終止條件，其計算流程如圖3所示。

1）初始染色體種群

2）計算適應度函數

適應度函數用于判斷種群中每一條染色體的優劣情況，本算例中可采用目標函數F（GNi）作為適應度函數，函數值越低則表明該染色體質量愈優秀。

3）選擇種群

在父代種群挑選出一組染色體，用于產生下一代種群。本算例中采用精英保留策略的錦標賽篩選法，即對于隨機排列的染色體種群，按順序每兩個一組進行適應度函數對比，保留適應度高的一條染色體，最終保留父代種群的一半染色體。

4）復制計算

將父代染色體中經過選擇種群所篩選出的染色體原狀態復制至新一代種群中，以保留父代種群中的優良染色體。

5）交叉計算

為生成新一代染色體時保留父代種群中的優良基因，對復制計算得到的種群每兩條染色體進行交叉計算。交叉過程為：對于相同的葉片編號，則在新染色體中保留該編號；對于不同的葉片編號，則隨機選擇一個寫入新染色體；對于空余的部分，則由尚未分配的葉片編號隨機排列后寫入新染色體，生成的新染色體寫入新一代種群中。

6）變異計算

為避免迭代計算陷入局部最優的情況，需對經過復制和交叉所得到的染色體種群執行變異計算。變異過程為：在染色體中隨機選取數量不等的基因，并對其隨機重新排序，變異后的結果寫入新一代種群中。

7）優選計算

對于新一代種群，按適應度函數值由低至高進行排列，排列后按順序保留前i個染色體，并對染色體隨機排序，至此完成新一代染色體種群的建立。

3 仿真與試驗分析

以某型APU的渦輪組件為研究對象，測得渦輪盤的各項參數與葉片質量，如表1所示。

設置每代種群中染色體數量為100，分別設置四組迭代次數進行仿真，迭代次數分別為A組40次、B組60次、C組80次、D組100次，代入遺傳算法中進行計算，并繪制出每次迭代后生成種群中最優染色體的適應度函數值，得到四組程序的收斂狀態圖線，如圖4所示。

由圖4可看出，在迭代計算過程中，隨著迭代次數的增加，其適應度函數值呈收斂趨勢。由于加入了交叉與變異計算過程，該算法可以很好地避免陷入局部最優搜索狀態，理論上只要種群中染色體數量與迭代次數足夠多，總能尋找到全局最優解。但隨著染色體數量及迭代次數的增加，計算機運行耗時也將增加。為獲取染色體數量、迭代次數與系統耗時之間的關系，在程序中加入CPU運行時間監測函數，并繪制運行時間關于染色體數量、迭代次數之間關系的函數圖像，如圖5所示。

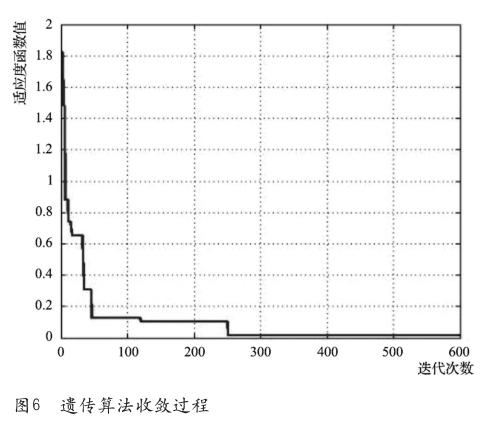
為滿足維修工作中的實際需求，根據計算機系統硬件水平設置相應的染色體數量與盡可能多的迭代次數，以獲取滿足工藝要求的排列方案。本例中再次設置染色體數量為100，擴大迭代次數為600，得到的收斂過程如圖6所示。

本次程序運行共計耗時15.3s，在第250次迭代時達到最終收斂狀態，此時葉片排列方案如表2所示。

將該渦輪組件在申克HM1BU型臥式平衡機上做平衡測試，根據維修手冊要求，設置測量模式為靜平衡，最大允許不平衡量為0.014ozin，轉速1000r/min，測試情況如圖7所示。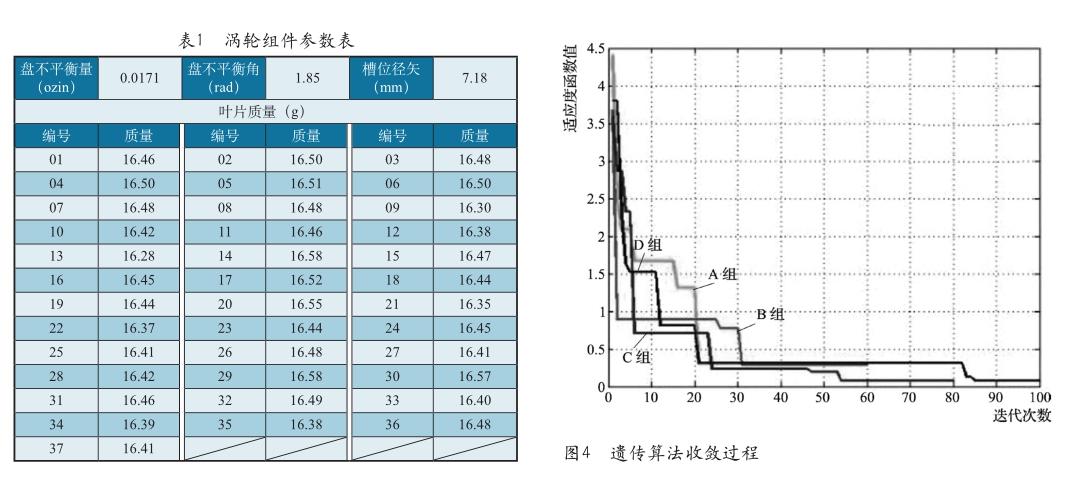

分別選取迭代次數為第10次、20次、40次、250次時的排列方案，在平衡機中進行測試，其不平衡量值變化過程及最佳排列時的平衡機顯示界面如圖8所示。可以看出，不平衡量實測值與算法的收斂趨勢保持一致。最佳排列方案時，測得渦輪組件不平衡量為2.53mozin，低于維修手冊要求的極限值，滿足維修工藝要求。

4 結論

針對APU渦輪組件的結構特點與修理工藝要求，對渦輪葉片的排序問題提出了結合精英保留策略的改進遺傳算法。計算結果表明，該方法具有很好的收斂速度、收斂穩定性與計算效率，計算程序易于實現，計算結果得到的排列方案能夠滿足維修工藝要求，可有效提高APU渦輪組件修理工作的質量與效率。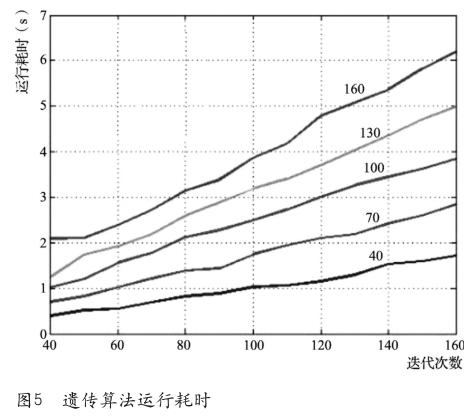

作者簡介

王冰，助理工程師，研究方向：APU維修與故障診斷。

趙鑫，助理工程師，研究方向：APU維修與故障診斷。

王璐璐，高級工程師，研究方向：APU維修與故障診斷。

參考文獻

[1] 彭國華，余遷，王罡. 混合遺傳算法在葉片排序問題中的應用 [J]. 西南民族大學學報·自然科學版，2006，32（1）：8-12.

[2] 朱獻文，李福榮. 求解旅行商問題的幾種智能算法 [J]. 計算機與數字工程，2010，38（1）：32-35.

[3] 沈崇圣. 遺傳算法中常用選擇算子在MATLAB中的實現 [J]. 上海應用技術學院學報，2003，3（3）：199-202.

[4] 廖明夫. 航空發動機轉子動力學 [M]. 西安：西北工業大學出版社，2015：90-107.