計算機動態測驗中問題解決過程策略的分析：多水平混合IRT模型的拓展與應用*

李美娟 劉 玥 劉紅云,4

(1北京教育科學研究院北京教育督導與教育評價研究中心, 北京 100036)

(2北京師范大學中國基礎教育質量監測協同創新中心; 3北京師范大學心理學部;4北京師范大學心理學部應用實驗心理北京市重點實驗室, 北京 100875)

1 引言

問題解決能力是指在沒有清晰解決方法的情境下, 通過一系列認知過程來理解和解決問題的能力(Mayer, 1982)。在這個過程中, 問題解決者必須充分理解問題的核心, 設計可行方案并實施, 且能夠控制進度并達到目標(Garofalo & Lester, 1985)。問題解決能力對于學習和取得成功非常重要, 很多全球范圍的大型教育測評項目都將其作為評價的重點。例如, 國際學生測評項目(Programme for International Student Assessment, PISA) (OECD, 2003,2013)等。近年來, 信息技術的進步和計算機測驗領域的研究為問題解決能力提供了全新的測評方式。如2012年PISA采用計算機動態測驗的方式, 通過模擬真實生活情境中的問題來考察學生的問題解決能力, 關注在沒有明確解決方案的情況下學生運用一般認知過程的特征(OECD, 2013), 強調問題解決過程的動態變化和互動特征(Funke, 2001)。

計算機測驗不僅可以改變測驗設計、施測方式,甚至可以改變數據分析的方法(DiCerbo & Behrens,2012)。不僅可以考察學生是否正確作答, 而且可以通過系統自動記錄基于時間的行為序列(Kerr,Chung, & Iseli, 2011), 記錄學生解決問題過程中的時間以及學生完成任務的系列行為, 稱為過程性數據(process data) (Zoanetti, 2010)。基于過程性數據不僅可以分析挖掘學生的解題過程策略, 同時也可以作為問題解決能力評價的證據(DiCerbo & Behrens,2012)。例如, Greiff, Wüstenberg和Avvisati (2015)基于PISA2012《室溫控制》任務的過程性數據, 發現一次只改變一個操作變量的策略不僅能預測學生在該題上的表現, 也能預測問題解決總成績。近年來, 隨著測量理論和統計技術的發展, 問題解決過程及其技能和策略的探討越來越被重視。其中一類是通過對該題目所需技能(或屬性)進行標定, 基于一定的測量模型對解決問題過程的策略特點進行分析。最具代表性的方法是認知診斷模型的評估。如de la Torre和Douglas (2004)采用高階潛在結構模型, 對學生能力進行估計, 并基于學生的認知屬性掌握模式對其認知特征進行分類。另一類是借助統計模型和數據挖掘的思想, 對過程數據蘊含的豐富信息進行分析。常用的方法有可視化分析方法(DiCerbo, Liu, Rutstein, Choi, & Behrens, 2011)、聚類分析方法(Bergner, Shu, & von Davier, 2014)和分類分析方法(Desmarais & Baker, 2012)。最近, 也有學者(Shu, Bergner, Zhu, Hao, & von Davier, 2017)結合隱馬爾科夫模型(Hidden Markov Model)和項目反應模型, 分析過程性數據中的序列作答信息,從而估計學生的能力。本研究探討的方法屬于第二類, 即基于過程數據分析學生在解決問題過程中的不同策略, 同時基于任務提交狀態的信息進行能力估計。

過程性數據具有嵌套結構, 每個學生完成任務過程產生的行為序列(即, 過程水平的數據)嵌套于學生個體。因此, 可以借鑒多水平框架下的模型來分析過程性數據(Goldstein, 1987)。多水平混合項目反應理論模型(Multilevel Mixture Item Response Theory, MMixIRT)將多水平模型和混合項目反應理論模型相結合, 不僅可以提高模型參數估計的精確性, 同時可以獲得不同潛在類別群體的測量特征(Cho & Cohen, 2010)。對于兩水平的數據, MMixIRT可以在第一水平和第二水平進行非連續潛在變量(潛在類別)和連續潛在變量(能力)的分析, 第一水平的潛類別分析主要基于被試作答反應之間的關系, 第二水平的潛類別分析主要基于組內被試作答反應之間的關系(Vermunt, 2003)。雖然 MMixIRT為分析嵌套數據和類別特征提供了思路, 但是如果直接處理過程數據, 可能會帶來兩個問題：(1)過程中的一個步驟僅反映了被試在這一時間點的一次操作或行為表現, 不滿足模型關于不同時間點的測量都是某一特質在這一時刻表現的假設。(2)采用問題解決的所有過程數據估計被試個體能力, 會帶來問題解決不同階段或不同步驟所測量特質的不統一而導致的估計值的偏差和解釋上的困難。因此,傳統的MMixIRT模型在模型假設和潛變量意義的解釋上并不適用于過程性數據, 如何借助該模型的思想使其適用于處理過程數據是拓展模型擬解決的問題。

國際上已經有越來越多的研究關注過程性數據的挖掘, 分析不同群體學生解決問題的典型特征(Qiao & Jiao, 2018; Liao, He, & Jiao, 2019), 但是大多數研究只采用了學生作答的部分信息, 或者只關注類別而忽略了能力估計。很少有研究基于過程數據的嵌套特點, 同時關注問題解決策略類別, 以及個體層面信息所反映的問題解決能力水平。本研究以 PISA2012中一道問題解決題目為例, 基于5個國家(或地區, 以下簡稱地區)學生問題解決的過程性數據, 將 MMixIRT模型進行拓展, 并使用拓展后的MMixIRT模型分析學生在問題解決過程中的不同策略, 估計個體水平能力, 同時也對各地區使用策略的特點進行總結和比較。

2 拓展的MMixIRT模型

傳統 MMixIRT模型的定義和詳細介紹參見(Cho & Cohen, 2010)的研究。本研究對傳統的MMixIRT模型做了兩方面的修改和拓展。

首先, 為體現問題解決任務過程中行為序列連續性的特點, 將步驟的累計信息作為特定步驟的過程數據。可以表示為：

其中 ytki為第 k個學生 t時間點在 i得分點(類似于后面交通題目中的路徑)上的操作行為。傳統的 MMixIRT模型是直接對 ytki建模, 而拓展的MMixIRT模型是對累計反應 Yjki進行建模。如果時間t=j, wt=1, 否則 wt=0, 則變為傳統的MMixIRT模型。結合測試題目和過程數據的特點, 采用累積反應作答作為過程j的反應作答, 即如果t≤j, 則wt=1。

其次, 為使得過程水平和個體水平變異的分解更加靈活, 定義設計矩陣A分解過程層面和個體層面的變異, 其中第j行 Aj用來定義過程數據不同層面潛變量的分解權重。拓展模型可以表示為：

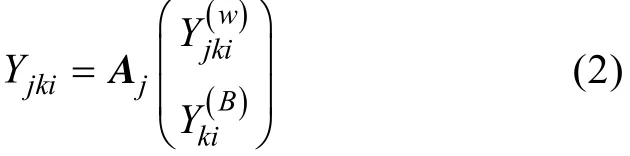
傳統模型是拓展模型的特例。拓展模型和傳統模型的區別主要表現在以下兩個方面：(1)過程水平每一步驟的潛在類別是前面各個步驟的累積狀態,而不是這一個步驟的表現, 描述累積狀態不僅可以更好地解釋解題過程策略的使用, 而且可以為探索策略使用的連續性和轉換提供依據; (2)個體水平潛變量的定義所采用的測量指標與傳統的 MMixIRT模型不同。傳統模型中, 個體水平的潛變量是由第一水平的觀測變量[yjk1, …, yjki, …, yjkI]估計得到(Lee, Cho, & Sterba, 2017), 而拓展模型中可以定義更加自由的設計矩陣 A決定個體層面能力估計所用到的信息。

3 本研究使用的拓展MMixIRT模型

拓展的 MMixIRT模型比較靈活, 可以在第一水平和第二水平模型中結合實際研究關注的重點定義不同的模型。結合過程數據的特點, 本研究主要關注學生在問題解決過程解題策略的差異和最終狀態體現出個體能力的差異, 因此, 本研究使用的模型也是上述拓展模型的特例。

3.1 模型定義

本研究使用的拓展 MMixIRT模型包含兩個水平：過程水平和個體水平。在過程水平, 定義潛類別來描述不同步驟的異質性, 從而對不同策略進行分類; 在個體水平, 定義連續潛變量來估計個體的能力。

過程水平模型：

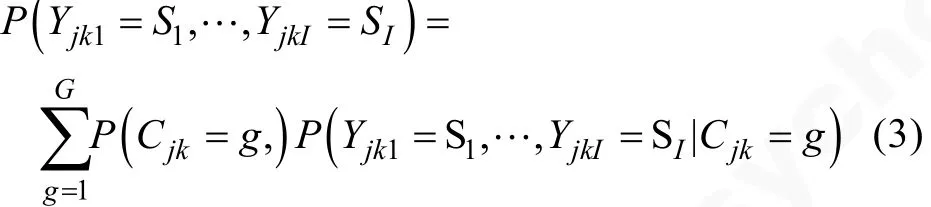
P（ Yjk1=S1,… ,YjkI=SI）表示第 k個學生(k=1,…,K)在第j個步驟(j=1, …,Jk, Jk表示學生k的步驟總數)后, 得分點上的作答狀態為(S1,…,SI)的概率(需要注意的是, 每個學生完成任務所使用的步驟數 Jk是不同的); 其中 P （ Cjk= g）表示第 k個學生的第 j個步驟屬于潛在類別 g的概率(g=1,2,…,G), G 為潛在類別數。 P ( Yjk1=S1,… ,YjkI=SI|Cjk= g)表示第 k個學生的第 j個步驟屬于潛在類別g的條件下, 前面j個步驟的累積作答狀態為(S1,…,SI)的條件概率。

個體水平模型：

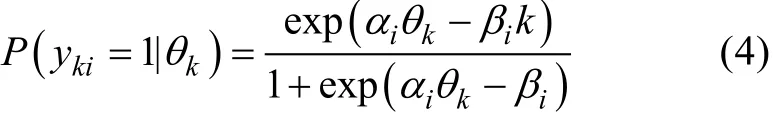
個體水平模型表示基于學生最終作答狀態對個體水平的能力進行估計, 對應的設計矩陣A為：如果 j為被試最后一次提交狀態的作答, 則Aj=（1,1）, 否則 Aj=（1,0 ）。在個體水平模型中, yki表示第k個學生在第i得分點上的作答。αi表示第i得分點的區分度參數, βi表示第i得分點的難度參數(i = 1,2,…,I), θk表示基于過程中最后一個步驟估計得到的學生k的能力估計值。假設θk服從標準正態分布(θk～N(0, 1))。

圖1表示本研究使用的拓展MMixIRT模型的基本結構。圖中的方框表示學生在過程中的作答反應, 圓形表示潛變量, 三角形中的 1表示元素均為1的常數向量(這一常數向量的系數對應截距參數βi,即傳統IRT模型中的難度參數)。其中, 對于過程水平, Cjk是分類潛變量, 對于個體水平, θk是連續潛變量。在過程水平, 學生k在第j個步驟上對所有路徑的作答[yjk1,…,yjki,…,yjkI]可以由分類潛變量 Cjk解釋; 在個體水平, 學生對所有路徑的最終作答[yk1,…, yki,…,ykI]可以由連續潛變量θk解釋。根據方程(4), 在個體水平中, 從連續潛變量θk指向每條路徑反應狀態的箭頭描述了能力 θk的變化對選擇這條路徑概率的影響, 對應于區分度參數(αi), 而從三角形指向每條路徑的箭頭θk表示為0時, 這條路徑的選擇概率, 對應于傳統IRT模型的難度參數(βi)。

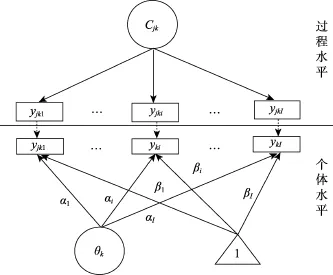
圖1 本研究使用的MMixIRT模型示意圖

3.2 參數估計的返真性與分類準確性

采用Monte Carlo模擬研究對本研究所采用的模型參數估計的返真性和分類準確性進行了檢驗。設計考慮2個影響因素：(1)過程水平的潛類別數(3個, 5個); (2)個體完成任務的過程步驟數(30步, 50步), 共2×2=4種實驗條件。使用 R 語言自編程序,基于拓展MMixIRT模型產生每種條件下的反應數據 。 其 中 αi～ U （1,2 . 5）, βi～N （0,1）, θk～ N（0,1）(Wang, Xu, Shang, & Kuncel, 2018), 不同類別的反應概率參照Nylund, Asparouhov和Muthén (2007)的研究, 不同條件下各類別所占比例和題目(路徑)答對概率真值見附錄表1。每種條件下假設所有個體的過程步驟數相等, 其中最后一個步驟就是個體的最終作答狀態, 用于估計個體水平的能力。每種條件下被試數固定為600人, 數據重復模擬100次。使用 Mplus 7.11 軟件(Muthén & Muthén, 2005)估計模型的參數。

結果表明, 各參數返真性較好, 表現在各參數偏差都很小, 區分度參數均方誤差(RMSE)在0.2左右, 難度參數 RMSE在0.1以下, 能力參數RMSE在0.3左右。各條件下模型分類結果的準確性較高,均在96%以上。

4 數據分析

4.1 題目

本研究使用的是PISA2012問題解決測驗中一道交通問題的題目(Traffic CP007Q02)：地圖上標明了每條路徑所需的時間, 要求學生找到從Diamond到Einstein的最快路徑。正確的最短路徑需用時31 min,題目描述和路徑標識如圖2所示。

4.2 過程性數據編碼

上述過程性數據來源于data source： http：//www.oecd.org/pisa/data/。首先, 篩選與有效路徑點擊有關的信息。然后, 將“路徑選擇的情況”按照不同路徑進行拆分, 獲得23條路徑(P1, P2, P3…, P23)的點擊結果。表1是整理后的數據格式示例, 每一行代表一個學生作答過程中的一個步驟, 每一列代表一條路徑。其中, 0表示未選擇, 1表示選擇。例如,第一行表示編號為00017的學生在第1步選擇P2,第二行表示第2步選擇P1, 第三行表示第3步選擇P13, ……, 第八行表示第8步取消P1……

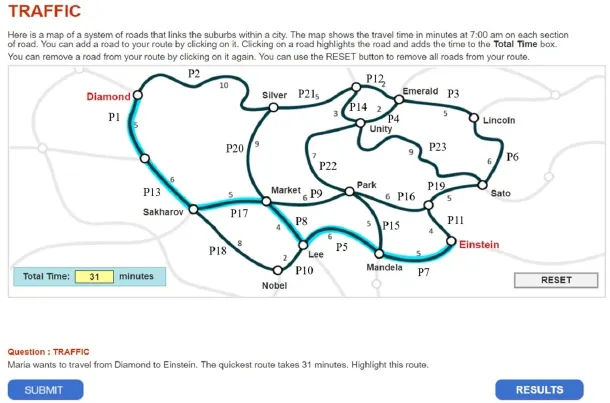
圖2 PISA2012交通問題題目及其正確路徑

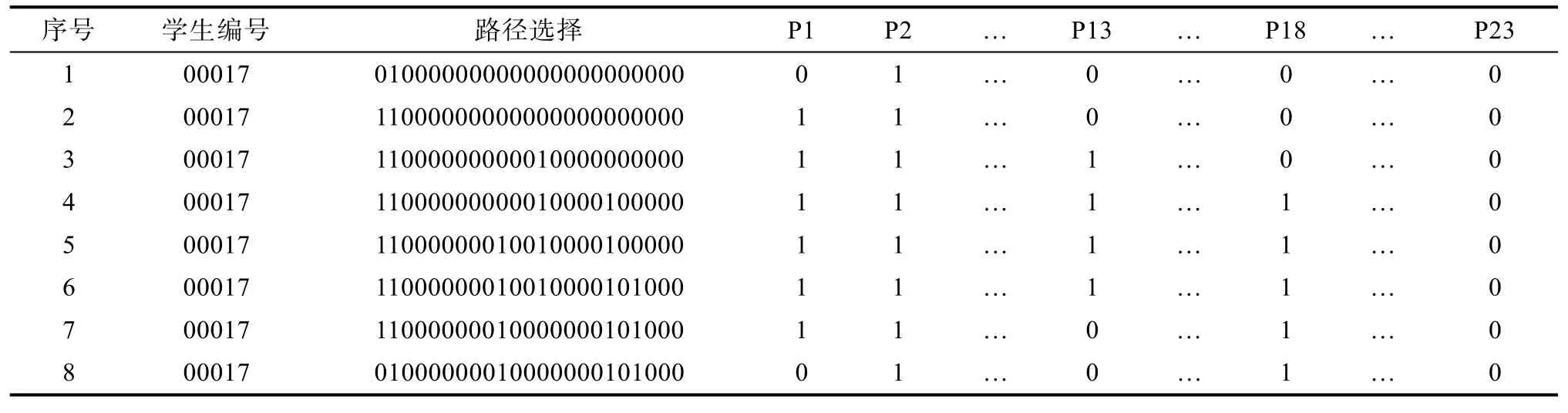
表1 整理后的過程性數據舉例

之后按照答案重新計分。與傳統試卷分析中的題目類似, 表1中的P1, P2, P3等23個變量代表23條路徑。正確路徑為：Diamond-Nowhere-Sakharov-Market-Lee-Mandela-Einstein, 即P1, P5, P7, P8,P13和 P17。對于過程中的每一步作答, 如果學生選擇正確路徑, 則該路徑計分為 1, 否則計分為 0,同理, 如果選擇了錯誤路徑, 則該路徑計分為 0,否則計分為1。編碼后的23個變量命名為CP1, CP2,CP3,…, CP23。表2呈現了編碼后的數據格式示例。例如, 第一行表示編號為00017的學生在第一步選擇P2, P2為錯誤路徑; 第二行表示第2步選擇P1,P1為正確路徑等。

4.3 樣本

本研究樣本來自 PISA2012問題解決測驗中 5個地區的3196名15歲學生。其中加拿大、中國香港、中國上海、新加坡和美國的樣本量分別為1449、433、411、456、406。5個地區共有139990條過程步驟, 學生的平均步驟數為43.80 (SD = 38.06), 其中最小值為1, 最大值為335。學生作答的平均反應時為669.22 s (SD = 543.12 s), 其中最小值為10.7 s,最大值為2384.7 s。

4.4 數據分析方法

采用拓展MMixIRT模型, 使用Mplus 7.11軟件對策略類別和個體能力進行估計。采用關聯規則挖掘探討不同策略類別之間的關聯。

關聯規則挖掘的目的如下：若兩個或多個變量之間存在某種規律性, 則它們之間存在關聯, 關聯規則挖掘就是尋找同一時間中不同出現項的相關性, 以求從大量的數據中抽取出隱含的信息。Apriori算法是一種常用的挖掘關聯規則的頻繁項集的算法, 其基本思想是從包含一個項的頻繁項集開始, 遞歸地產生具有兩個項的頻繁項集, 然后依次遞歸, 直到產生所有的頻繁項集(Peter, 2013)。本研究基于SPMF平臺采用Apriori算法進一步分析學生問題解決策略之間的關系。

4.5 變量

使用學生問題解決過程中與作答時間有關的三個變量(路徑點擊數、重設數量、反應時)與模型估計結果的相關進一步驗證模型估計結果的效度。其中, 路徑點擊數表示學生點擊路徑的數量; 重設數量表示學生取消前面所有路徑點擊狀態, 重新開始做題的次數; 反應時表示學生完成任務所用的時間。同時, 研究還選取了耗時與正確作答時間的差異, 表示最后提交狀態所選路徑耗時與正確作答時間(31 min)差值的絕對值。

5 結果

5.1 模型選擇

對于拓展的 MMixIRT模型的分析, 首先需要結合模型的擬合指標和潛在類別的可解釋性(Rosato& Baer, 2012)確定分類的個數。表3給出5個地區數據同時估計得到的類別數為 1～7的模型擬合指標。采用的擬合指標包括loglikelihood、AIC (Akaike,1974)、BIC (Schwarz, 1978)、aBIC (Tofighi & Enders,2008)和熵(Asparouhov & Muthén, 2014)。其中, 前4個指標越小表示模型和數據擬合越好, 熵是用來測量混合模型區分各潛在類別的程度的指標, 該指標越接近 1表示類別區分越好。從結果可以看出,潛類別數量越多, 模型擬合越好。但是, 在 7個類別的情況下, 有2個類別的路徑無法構成從起點到終點的完整路線。在6個類別的情況下, 有1個類別的路徑無法構成完整路線。因此, 結合擬合指標的結果和類別的可解釋性, 最終選擇5個潛類別的結果。

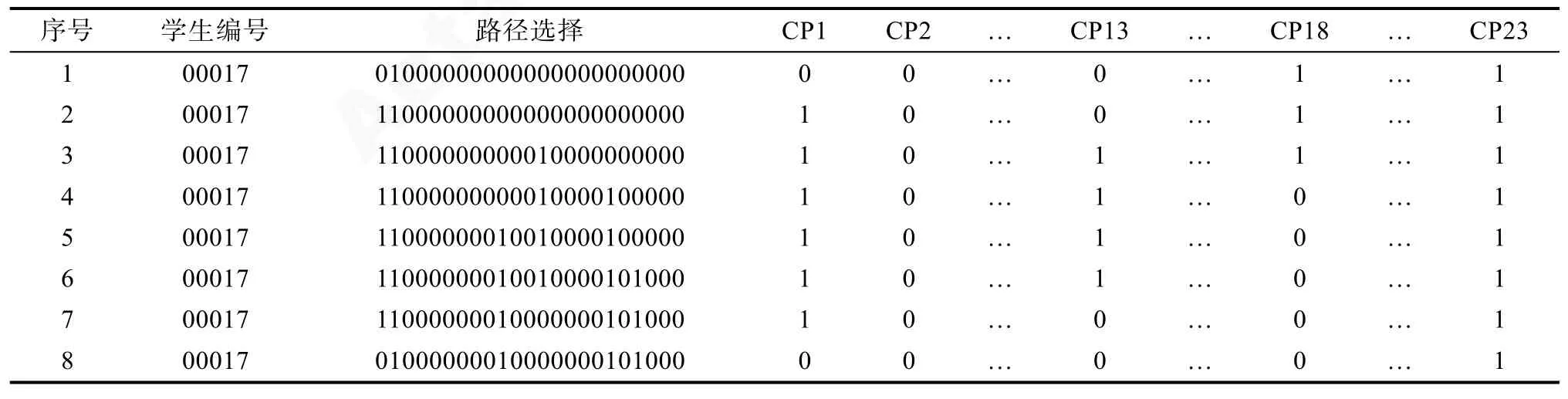
表2 編碼后的過程性數據舉例

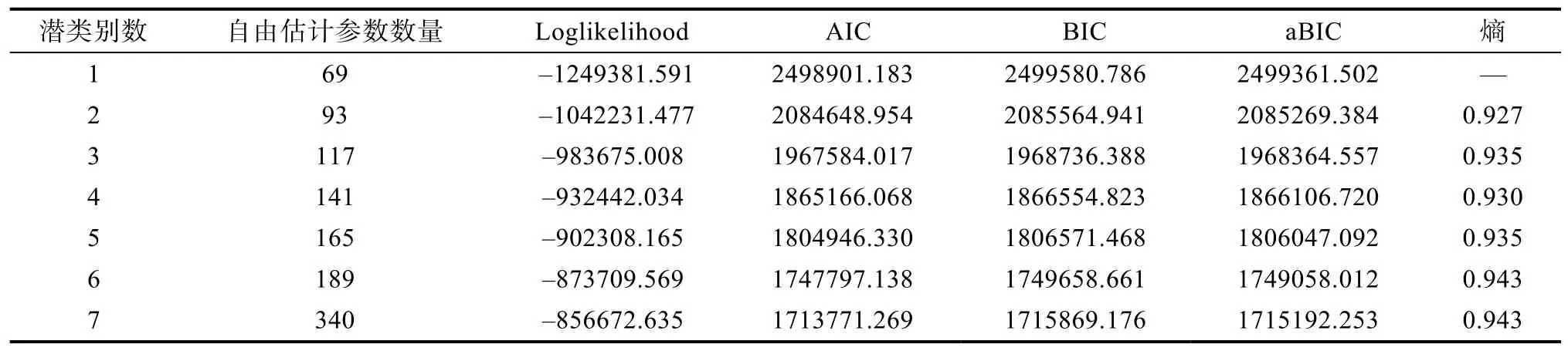
表3 模型擬合指標結果

5.2 策略類別特征及其與個體能力水平關系

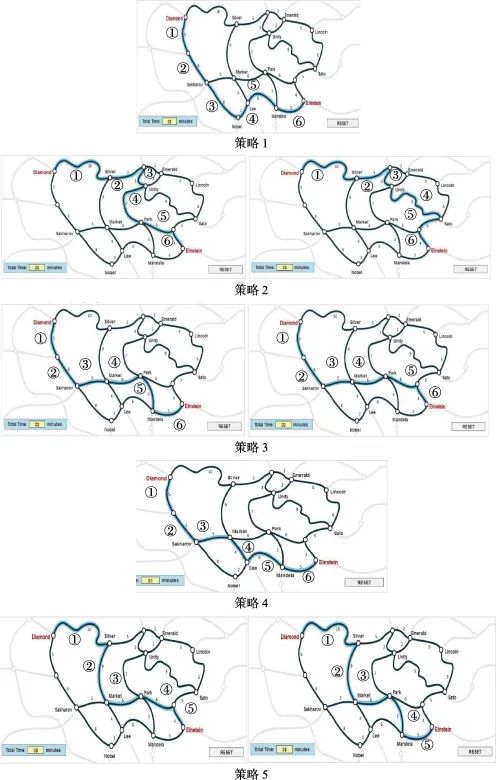
圖3 各策略選擇路徑情況

拓展的MMixIRT模型可以將學生每一步過程操作后所處的狀態分為5類, 各潛類別點擊各路徑的次數見附錄表2。分析各類別選擇頻率最高的路徑以及路徑之間的關聯, 可以形成這一類別的典型路徑。各類別所選典型路線以及順序如圖 3所示,其中圖中帶圈的數字表示路徑的順序, 每個類別代表一種解決問題策略。因為學生的每次操作行為存在關聯, 所以每次操作行為所屬的類別也存在聯系。如果相鄰兩步操作所屬類別不同, 則學生使用的策略發生變化, 即存在策略轉移。學生最后使用的策略與能力值有很高的相關, 如果使用正確策略,則會正確作答題目, 使用錯誤策略, 則會錯誤作答題目, 但是使用不同的錯誤類型策略, 能力值不同。

鑒于策略轉移的存在, 我們將每個學生最后一步屬于的策略作為其最終的策略, 分析不同策略下對應的能力估計值平均值, 得到5個策略對應的能力平均值分別為-0.714、-1.281、-0.714、0.399和-0.714。結合圖3可以看出, 策略4與正確路徑相同, 用時為 31 min, 個體的能力值也最高, 說明這是正確的策略; 策略 2所選路線是最遠的路線, 與正確路徑完全沒有重合, 用時為35或36 min, 與正確路徑作答時間差異最大, 個體的能力值最低, 說明這是最差的策略; 策略1、3、5與正確路徑有部分重合, 這些策略雖然選擇了不同的路徑, 錯誤類型不一致, 但是其個體的能力值相等, 說明這些策略在優劣程度上差異不大。

表4呈現了各地區學生在這道題目上最后一步所用策略的分布情況。可以看出, 最后一步為策略4 (正確路徑)的學生比例最高, 為策略2 (能力最低)的學生比例最低。從不同地區來看, 新加坡學生在最后一步上使用策略4的學生比例為81.6%, 略高于其他地區, 說明新加坡學生在這道題上表現最好,而美國學生在最后一步上使用策略4的學生比例為75.6%, 略低于其他地區, 而最后一步采用策略 2的比例都高于其他地區, 說明美國學生表現相對較差, 這與個體能力水平估計的均值結果是一致的。另外, 不同地區錯誤組學生在最后一步使用的策略上呈現出不同的特點。例如, 加拿大學生較多使用策略 3, 新加坡和中國上海學生較多使用策略5和3, 而美國學生較多使用策略1, 中國香港學生較多使用策略1和3。

5.3 策略應用情況

為了探討過程數據中策略的變換, 研究將學生在過程中連續使用某種策略3次或以上定義為明顯使用了該種典型策略。在描述策略轉換中只記錄了不同策略之間的轉換, 如果轉換過程中同樣的策略出現了多次, 只記錄最后一次轉換。表5呈現了各地區正確組和錯誤組學生在解題過程中應用策略數的情況。總體來看, 正確組學生在解題過程中應用策略數為4和5的情況最多。正確組學生中應用5種策略的人數比例明顯大于錯誤組。說明在正確組中, 有接近三分之一的學生是通過嘗試所有5種策略才找到正確路線。而錯誤組有超過三分之一的學生嘗試了4種策略即停止作答, 提交了錯誤的路線。從各地區比較來看, 新加坡和美國正確組應用5種策略的學生比例低于其他地區, 其中美國最低。

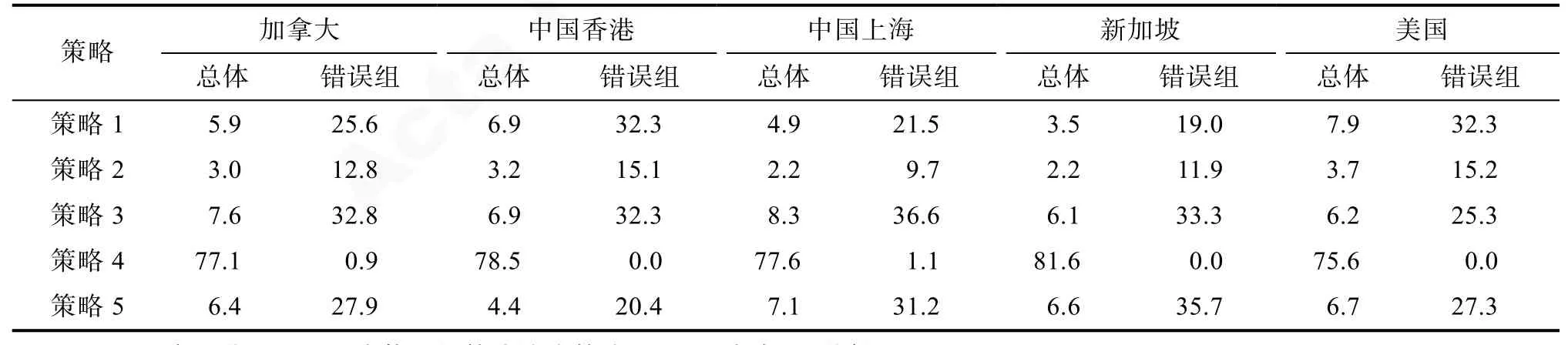
表4 各地區學生解題最后一步所用策略分布比例(%)

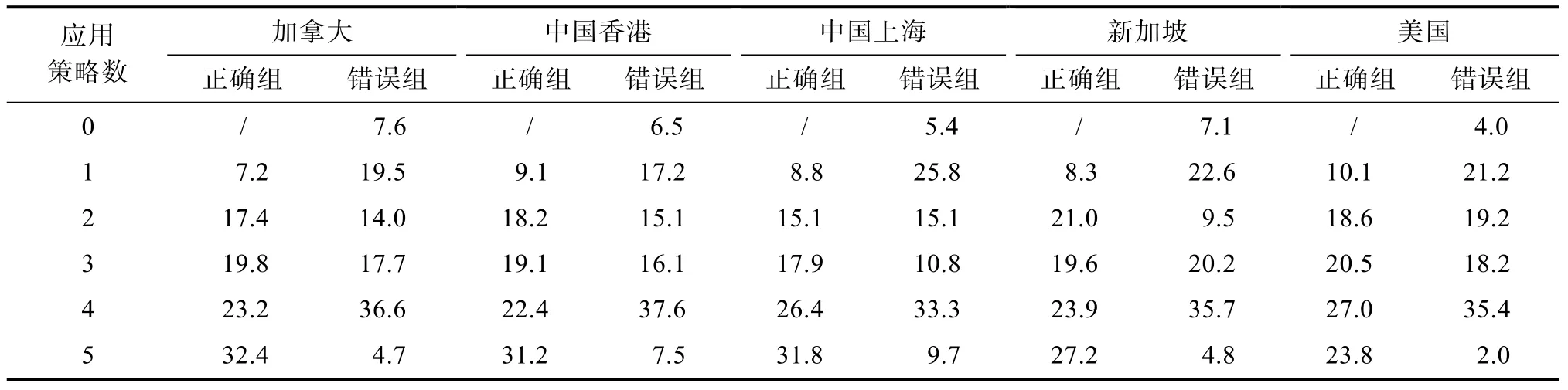
表5 各地區問題解決過程應用策略數分布比例(%)

為了進一步分析策略之間的關系, 表 6和表 7呈現了 Apriori算法的關聯分析結果。頻繁項集指頻繁同時出現的兩種策略, 頻次表示這兩種策略同時出現的次數。置信度是指包含前項和后項的事務個數在包含前項的事務總數中的比例。例如, 5==>1表示同時使用策略1和策略5的學生人數占使用策略5學生人數的比例。根據表9結果可以看出, 在正確組學生的策略使用規則中, 策略3和5, 策略3和4, 策略2和5, 策略1和5具有較強的關聯關系。例如, 對于使用策略 5的學生來說, 同時使用策略3的概率為 0.51。與正確組學生不同的是, 錯誤組學生的策略使用規則中, 策略3和4存在較弱的關聯, 即錯誤組學生能夠將策略3轉換到使用正確策略4的概率較低。另外, 對于使用策略5的學生來說, 使用策略3的概率明顯低于正確組學生。根據表7可以看出, 各地區正確組和錯誤組學生使用策略規則基本一致, 但是中國上海的正確組學生表現出不一致的策略使用規則, 具體來講, 使用策略 2的學生使用策略5的概率、使用策略3的學生使用策略5的概率明顯高于其他地區; 使用策略4的學生使用策略3的概率、使用策略3的學生使用策略4的概率明顯低于其他地區。

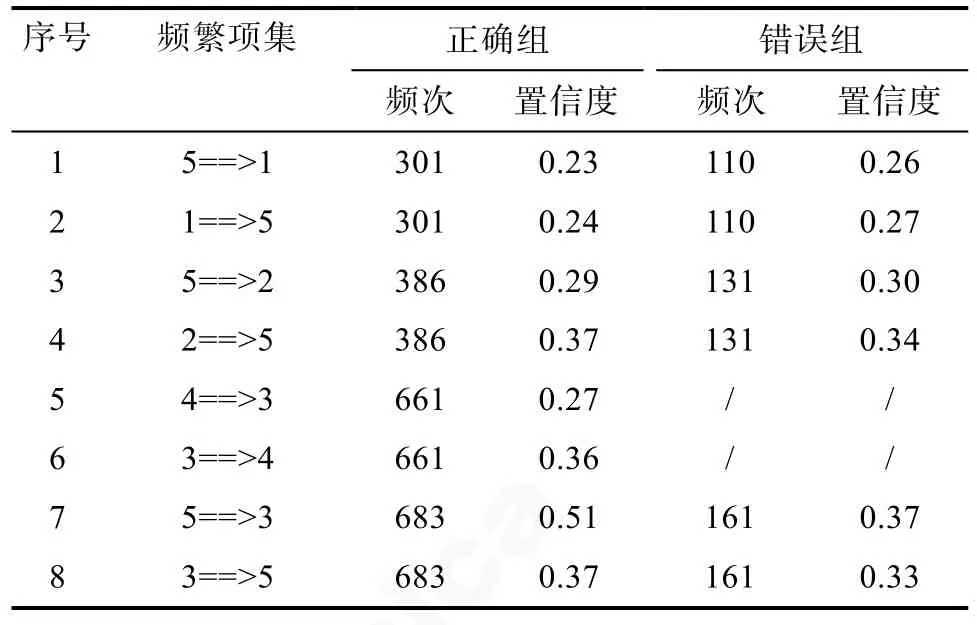
表6 學生總體應用策略之間的關系

5.4 過程性變量和能力的關系

表8呈現了路徑點擊數、重設數量、耗時與正確作答時間的差異、反應時這些過程性變量以及個體能力值的描述性統計指標, 及過程性變量與個體能力值的相關。從表8中可以看出, 對于所有地區,正確組的路徑點擊數小于錯誤組, 正確組的重設數量小于錯誤組, 正確組和錯誤組的反應時沒有顯著差異。耗時與正確作答時間的差異越大, 個體能力估計值的平均水平越低。另外, 結果還反映了不同地區在完成題目過程中的特點。從描述統計方面來看, 各地區呈現出了不同的典型特征, 例如, 美國學生個體能力估計值的平均水平最低, 路徑點擊數最少, 錯誤組耗時與正確作答時間的差異明顯大于其他地區; 而新加坡學生個體能力估計值的平均水平最高, 但是平均反應時也最長。

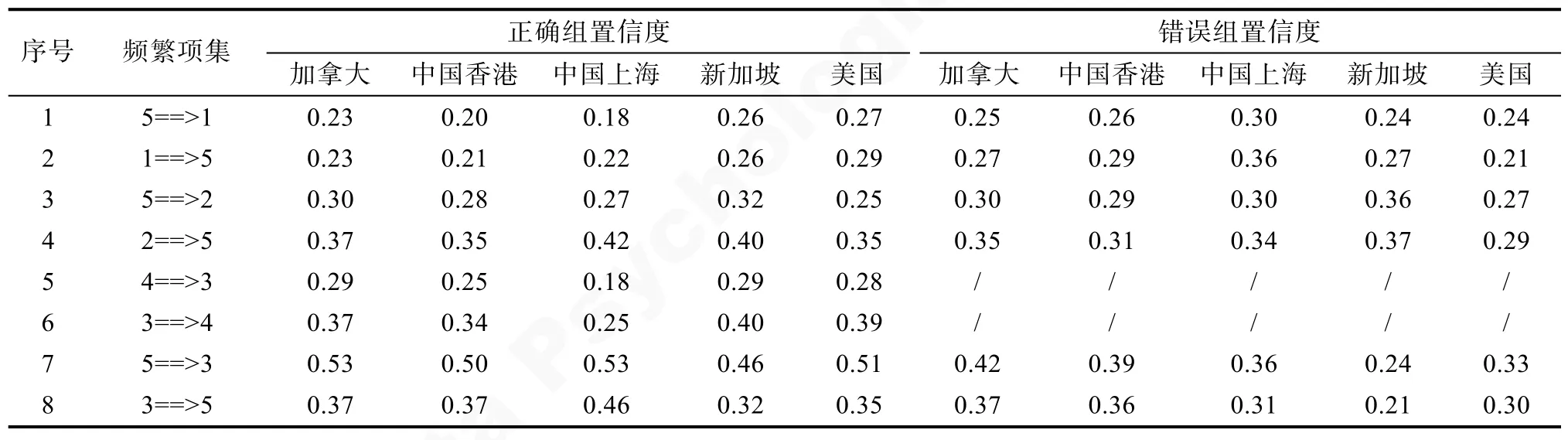
表7 各地區學生應用策略之間的關系

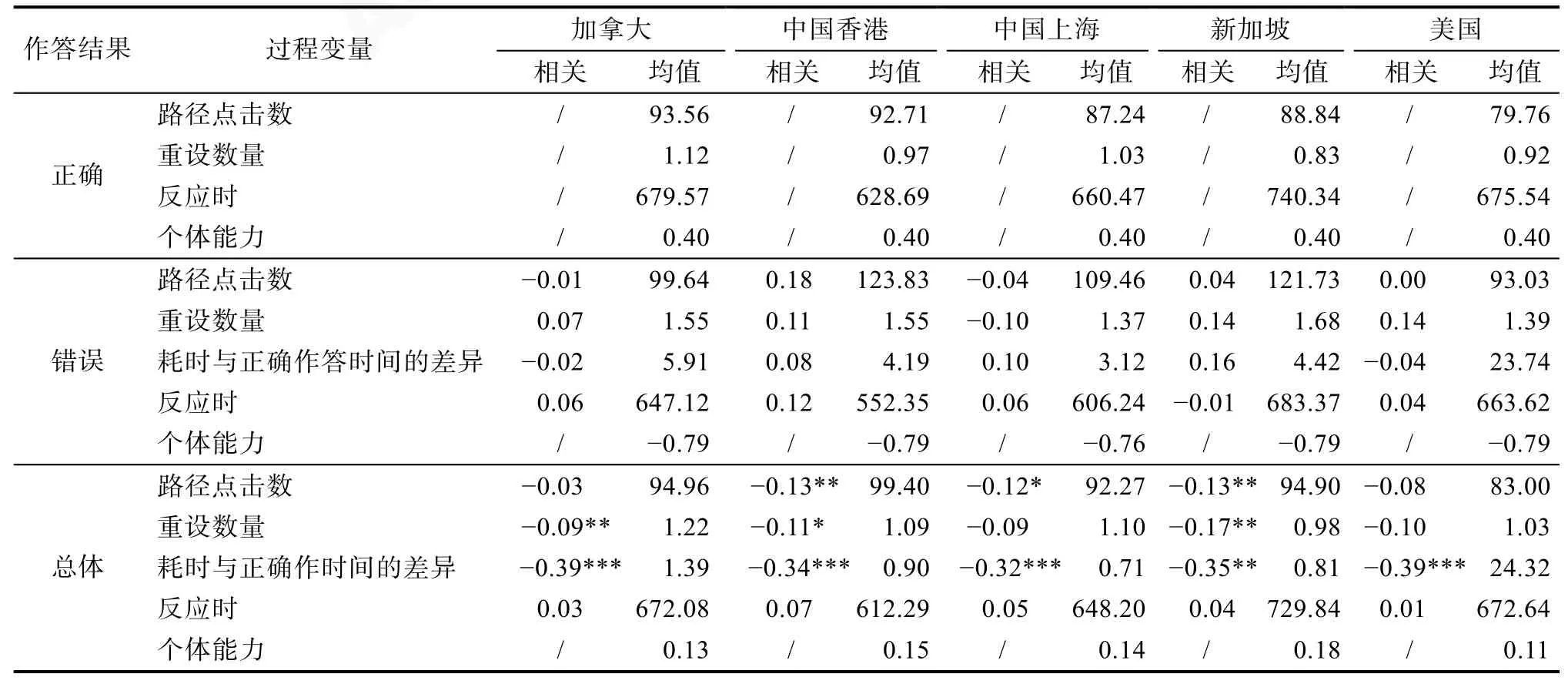
表8 過程變量的描述統計及其與個體水平能力估計值的相關

6 討論與結論

拓展的MMixIRT模型結合了IRT模型、潛類別模型和多水平模型的特點, 不僅可以在過程水平分析策略類別特征, 而且還可以在個體水平估計能力值。在過程水平, 使用潛類別模型確定學生解題的過程策略, 深入探討策略應用的情況; 在個體水平, 使用IRT模型估計學生的個體能力值。模型優勢在于能夠同時描述過程水平和個體水平的信息。過程水平中的策略分析能夠得到不同群體在問題解決過程中的典型行為模式和思維特點, 從而更好地為提高學生的問題解決能力提供有針對性的信息。另外, 拓展 MMixIRT模型具有良好的參數返真性和較高的分類準確性, 能夠應用于過程性數據的分析。

研究將拓展的MMixIRT模型應用于分析5個地區學生完成問題解決題目的過程性數據, 驗證了該模型結果的合理性和可解釋性。首先, 操作步驟特征可分為5種策略, 體現了問題解決過程中不同能力水平學生的特征。策略 4是正確的解題策略,最后一步為策略4的學生比例越高, 平均能力水平也越高。策略2是距離正確路徑最遠, 耗時最長的策略, 即最差的策略。最后一步為策略2的學生比例越多, 平均能力水平也越低。其次, 關于策略應用和轉換的結果體現了學生解決問題過程中試誤策略的應用, 這與現實中問題解決策略的使用一致。在正確組中, 學生在解題過程中應用策略數為4次、5次的情況最多, 說明學生通過不斷轉換策略完成題目, 很少有學生只使用一種正確策略直接解決了問題。另外, 最典型的正確組學生策略使用規則是從策略3轉換到策略4。也就是學生先選擇了與正確路線重合的前三條路徑, 然后在下一條路徑上, 沒有選擇從Market到Lee, 而是從Market到了Park (見圖3, 后面三條路徑的用時加起來為16 min,大于正確答案后三條路徑的用時15 min。然后學生可能發現存在比這樣走用時更短的路線, 于是從策略3轉換到了策略4, 即從Market改為走向Lee, 從而選擇了正確答案的路線。而在錯誤組中, 學生在解題過程中應用策略數為4的情況最多, 但是較少的學生堅持嘗試了5種策略。最后, 操作過程變量與策略和能力之間關聯分析的結果, 證實了這一模型分析過程數據的有效性。部分過程性的變量與個體的問題解決能力有顯著相關, 結果表明, 除過程中學生策略選擇外, 其他過程變量(例如, 路徑點擊數、重設次數等)也均在不同程度上與學生的問題解決能力存在相關。

研究還關注了不同地區間過程水平和個體水平分析結果的比較。首先, 各地區在過程性變量上呈現出不同的特點, 例如, 美國學生問題解決能力最低, 路徑點擊數最少, 錯誤組耗時與正確作答時間的差異明顯大于其他地區, 而新加坡學生問題解決能力最高, 反應時也最長。從文化差異上來看,西方文化背景下學生關注個人價值以及個體的好奇心和興趣, 而儒家文化背景下學生關注個體努力程度, 他們認為努力是實現成功的必備因素(Li,2012)。此題考查的是問題解決的計劃與執行部分,如果學生不斷努力試錯, 也可以得到正確答案。努力程度(工具性動機)會促進學生問題解決的表現。這也可能是新加坡、中國上海、中國香港學生的問題解決能力較高的原因。而新加坡學生問題解決表現最好, 主要源于新加坡的整體課程設計注重學生的問題解決能力, 將問題解決能力系統納入課程,例如, 其在中小學數學大綱中在數學過程部分, 明確列出了思維技能和問題解決策略(Fan & Zhu, 2007)。因此, 在策略使用上, 新加坡正確組應用 5種策略的學生比例明顯低于其他地區, 說明新加坡學生解決問題典型特征是思考時間比較長, 使用策略數相對較少而得到正確答案。而美國學生正確組應用5種策略的學生比例也較低, 解決問題典型特征是思考時間比較少, 但是并未像其他地區一樣, 去嘗試足夠多的策略最終得到正確結果。其次, 加拿大、中國香港、中國上海、新加坡錯誤組學生在最后一步較多使用策略 3。從策略應用的結果可以看出,很多作答正確的學生都是從策略 3轉到了策略 4,說明對這些解題錯誤的學生, 如果再給予更多的思考時間, 有很大的可能最終轉換為正確的策略。這些結果可以為教學和訓練提供更加豐富的信息, 幫助教師給予有針對性的指導。綜上, 過程性數據分析的結果一方面能夠給教育測量研究者和測驗題目研發者提供更多信息, 以便進行命題改進, 另一方面, 這些信息還可以被納入測驗計分體系, 測驗計分不再只基于學生個體的最后作答, 而結合了學生策略的使用, 這將在一定程度上豐富測驗分數的含義。

拓展的 MMixIRT模型比較靈活, 可以在實際中結合題目的特點和關注的重點定義不同的模型。首先, 可以在模型的個體水平中加入描述學生類別特征的潛類別, 也可以考慮在過程水平中加入描述步驟能力的連續潛變量, 探討學生在解題過程中能力的變化情況(Liu, Liu, & Li, 2018)。其次, 還可以在模型加入能夠減少測量誤差并能預測學生問題解決能力的其他協變量, 例如學生的動機等(Fox &Glas, 2003)。最后, 本研究為單任務情境, 當分析對象為多任務時, 可以將其拓展為三水平模型, 分別為過程水平、任務水平和個體水平, 同時考察不同任務情境問題解決策略的應用以及多任務情境下個體能力估計。

本研究具有一定的局限性。首先, 在策略轉換分析時, 將使用某種策略3次或以上定義為使用了該種典型策略, 這樣的定義也損失了一部分不穩定的策略轉換的信息。如果這種不穩定的策略轉換也是考察的對象, 可以將這些信息納入策略轉換的分析中。其次, 分析過程中只是將單一的路徑作為分析的單元, 沒有考慮可能的路徑組合(如某些情況下, 不同路徑之間的鏈接是唯一的, 可能將這些路徑合起來分析更加合理), 可以在未來的研究中考慮不同路徑組合轉換的模型。另外, 這一模型在復雜問題解決過程中的普適性尚待進一步檢驗, 使用MMixIRT模型的前提是需要將過程性數據編碼為類似本研究中的數據結構, 實際中可能某些任務不太容易實現這樣的編碼轉換。

研究得出的主要結論如下：

第一, 拓展的 MMixIRT模型不僅可以基于行為序列分析學生解題過程中策略使用情況, 還可以在個體水平上提供能力估計值。

第二, 使用拓展的 MMixIRT模型可以對不同地區學生在解決問題時策略使用情況的典型特征進行分析, 為有針對性的訓練提供參考。

附表1模擬研究中各類別數量比例及題目答對概率

注：此處的題目答對概率是指除去最終作答狀態的所有過程步驟的概率, 真實值中最終作答狀態的分類與各潛在類別的特征一致。

潛類別數為3潛類別數為5題目 類別1(33.33%)類別2(33.33%)類別3(33.33%)類別1(20.00%)類別2(20.00%)類別3(20.00%)類別4(20.00%)類別5(20.00%)1 0.85 0.85 0.10 0.85 0.85 0.10 0.10 0.10 2 0.85 0.85 0.20 0.85 0.85 0.20 0.20 0.20 3 0.85 0.85 0.10 0.85 0.85 0.10 0.10 0.10 4 0.85 0.85 0.20 0.85 0.85 0.20 0.20 0.20 5 0.85 0.85 0.10 0.85 0.85 0.10 0.10 0.10 6 0.85 0.85 0.20 0.85 0.10 0.85 0.20 0.20 7 0.85 0.85 0.10 0.85 0.20 0.85 0.10 0.10 8 0.85 0.85 0.20 0.85 0.10 0.85 0.20 0.20 9 0.85 0.85 0.10 0.85 0.20 0.85 0.10 0.10 10 0.85 0.85 0.20 0.85 0.10 0.85 0.20 0.20 11 0.85 0.10 0.85 0.85 0.20 0.20 0.85 0.10 12 0.85 0.20 0.85 0.85 0.10 0.10 0.85 0.20 13 0.85 0.10 0.85 0.85 0.20 0.20 0.85 0.10 14 0.85 0.20 0.85 0.85 0.10 0.10 0.85 0.20 15 0.85 0.10 0.85 0.85 0.20 0.20 0.85 0.10 16 0.85 0.20 0.85 0.85 0.10 0.10 0.10 0.85 17 0.85 0.10 0.85 0.85 0.20 0.20 0.20 0.85 18 0.85 0.20 0.85 0.85 0.10 0.10 0.10 0.85 19 0.85 0.10 0.85 0.85 0.20 0.20 0.20 0.85 20 0.85 0.20 0.85 0.85 0.10 0.10 0.10 0.85

附錄2每個類別點擊各路徑的次數

路徑 類別1 類別2 類別3 類別4 類別5 路徑 類別1 類別2 類別3 類別4 類別5 P1 31050 1010 26185 10450 1175 P13 26422 535 27272 10874 276 P2 358 20917 272 71 26673 P14 70 12160 120 23 197 P3 14 4771 10 4 10 P15 766 1131 5969 345 4394 P4 16 1942 45 10 12 P16 740 3933 11056 158 9578 P5 10752 320 396 8981 4465 P17 836 430 28099 11113 785 P6 33 3751 24 17 19 P18 17576 266 374 64 157 P7 7554 1027 4109 6684 7135 P19 97 6384 196 11 549 P8 1082 241 433 11053 4972 P20 136 575 374 91 20809 P9 860 800 22245 154 14474 P21 80 21507 179 22 360 P10 15100 380 728 259 394 P22 60 5906 286 0 730 P11 1468 6723 7752 477 9474 P23 12 5436 120 2 6 P12 27 7128 33 10 84