典型雙坡低矮建筑屋面局部風(fēng)壓非高斯特性研究

，， ， ，

（1.結(jié)構(gòu)抗風(fēng)與振動(dòng)控制湖南省重點(diǎn)實(shí)驗(yàn)室，湖南 湘潭 411201；2.湖南科技大學(xué) 土木工程學(xué)院，湖南 湘潭 411201；3.湖南百利工程科技股份有限公司，湖南 岳陽 414000）

1 研究背景

我國東南沿海的農(nóng)村住宅主要為低矮建筑，其高度一般不超過24 m，位于大氣邊界層的最下層區(qū)域，該區(qū)域的風(fēng)場(chǎng)特性受地形起伏和周圍建筑物的影響較大。風(fēng)場(chǎng)中貼近地面的區(qū)域，因受地面粗糙程度的影響，氣流紊亂程度增加，從而導(dǎo)致作用于建筑表面風(fēng)壓時(shí)程的脈動(dòng)幅值間歇性顯著。有研究表明[1]，此時(shí)建筑所受的風(fēng)壓時(shí)程并不符合Davenport假設(shè)，而表現(xiàn)為明顯的非高斯特性。

大量災(zāi)后調(diào)查結(jié)果表明，低矮建筑的破壞主要是屋面破壞，且主要集中在屋檐、屋脊和角部等區(qū)域。而這些區(qū)域的氣流特性復(fù)雜，因此有必要對(duì)雙坡低矮建筑屋面在這些區(qū)域風(fēng)壓的非高斯特性進(jìn)行研究。

國外已有學(xué)者對(duì)風(fēng)壓的非高斯特性進(jìn)行了研究。如K.S.Kumar等[2]基于快速傅里葉變換，對(duì)低矮建筑非高斯風(fēng)壓時(shí)程進(jìn)行了模擬，并且將結(jié)果與不同屋面類型在不同條件下非高斯風(fēng)壓數(shù)據(jù)進(jìn)行對(duì)比，證實(shí)了模擬方法的有效性。F.Sadek等[3]基于實(shí)驗(yàn)數(shù)據(jù)，對(duì)低矮建筑表面的非高斯峰值風(fēng)壓進(jìn)行了研究，提出了設(shè)計(jì)上可以采用的非高斯風(fēng)壓極值估計(jì)方法。A.Kareem等[4]利用數(shù)值模擬方法，對(duì)比分析了不同計(jì)算模型和分析方法對(duì)湍流作用下低矮建筑表面風(fēng)壓的非穩(wěn)態(tài)、非高斯、非線性等特性研究的可行性和效果。Ko N.H.等[5]研究了方形建筑側(cè)面風(fēng)壓的非高斯特性，同時(shí)對(duì)高斯風(fēng)壓時(shí)程和非高斯風(fēng)壓時(shí)程進(jìn)行了模擬，并將模擬結(jié)果與實(shí)測(cè)數(shù)據(jù)進(jìn)行對(duì)比，分析了非高斯風(fēng)壓對(duì)方形建筑側(cè)面風(fēng)荷載的影響。

國內(nèi)也有部分學(xué)者對(duì)風(fēng)壓的非高斯特性進(jìn)行了相關(guān)研究。如王旭等[1]利用超強(qiáng)臺(tái)風(fēng)現(xiàn)場(chǎng)實(shí)測(cè)和風(fēng)洞實(shí)驗(yàn)相結(jié)合的方法，分析了低矮建筑屋面部分區(qū)域風(fēng)壓的非高斯特性。韓寧[6]、樓文娟[7]、莊翔[8]等分別基于風(fēng)洞實(shí)驗(yàn)，對(duì)不同體型的高層建筑的迎風(fēng)面和側(cè)面風(fēng)壓的非高斯特性進(jìn)行了分析，一致得出在側(cè)面迎風(fēng)等氣流分離程度大的區(qū)域非高斯性更加顯著的結(jié)論。羅穎等[9]探討了低矮建筑在不同屋面坡度、風(fēng)向角、高度及地貌條件下屋面風(fēng)壓特性的變化，分析了峰值因子的變化規(guī)律以及非高斯區(qū)分布特點(diǎn)理論，并且給出了峰值因子的簡(jiǎn)化計(jì)算式。

本研究擬利用風(fēng)洞試驗(yàn)，對(duì)A、B、C 3類地貌風(fēng)場(chǎng)下典型雙坡低矮建筑屋面風(fēng)壓非高斯特性展開研究，并結(jié)合屋面風(fēng)壓空間相關(guān)性對(duì)低矮建筑屋面流場(chǎng)特性與屋面風(fēng)壓非高斯特性的關(guān)系進(jìn)行闡述，給出屋面局部區(qū)域非高斯風(fēng)壓的產(chǎn)生原因，以期為低矮建筑圍護(hù)結(jié)構(gòu)抗風(fēng)設(shè)計(jì)提供一定的參考。

2 風(fēng)洞試驗(yàn)概況

2.1 試驗(yàn)設(shè)備及流場(chǎng)模擬

本研究的風(fēng)洞試驗(yàn)，在湖南科技大學(xué)風(fēng)工程試驗(yàn)研究中心大氣邊界層直流式風(fēng)洞中完成，試驗(yàn)采用的測(cè)壓系統(tǒng)包括PSI電子壓力掃描閥系統(tǒng)、三維脈動(dòng)風(fēng)速儀、皮托管和裝有PSI采集軟件的電腦。

利用尖劈、擋板、粗糙元等被動(dòng)模擬裝置，模擬出符合我國規(guī)范[10]規(guī)定的1:20縮尺比例的低矮建筑風(fēng)洞試驗(yàn)A、B、C 3類地貌風(fēng)場(chǎng)，其平均風(fēng)速剖面指數(shù)α分別為0.12,0.15,0.22。各風(fēng)場(chǎng)的風(fēng)速剖面、湍流度剖面模擬結(jié)果見圖1。由圖1可以得知，平均風(fēng)速剖面曲線符合GB5009—2012設(shè)計(jì)規(guī)范，湍流強(qiáng)度剖面理論曲線參考日本規(guī)范計(jì)算方法給出。A、B、C 3類地貌風(fēng)場(chǎng)參考高度處對(duì)應(yīng)的名義湍流度分別為12.2%,13.8%,23.2%。圖1中Hr為參考高度，Iu和Ur分別為參考高度處的湍流度和風(fēng)速，風(fēng)洞試驗(yàn)布置方式如圖2所示。

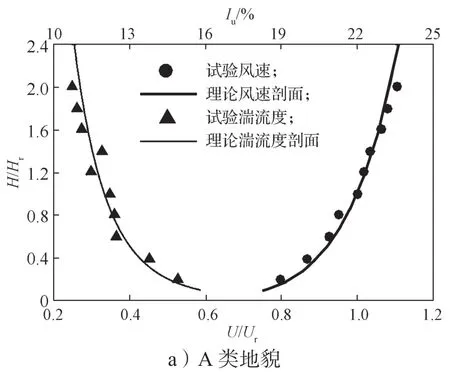
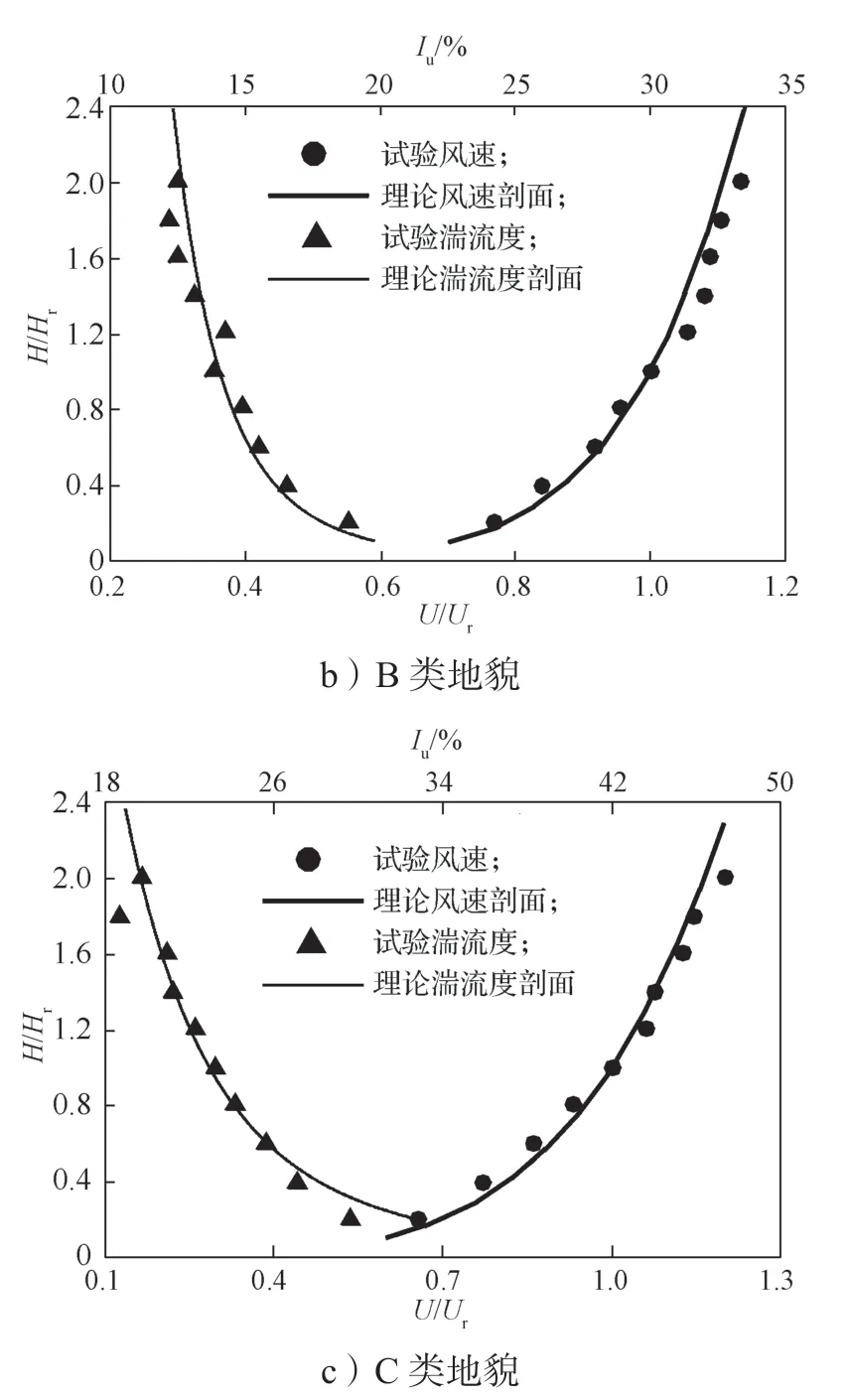
圖1 風(fēng)場(chǎng)模擬結(jié)果Fig.1 Wind field simulation results

圖2 風(fēng)洞試驗(yàn)布置圖Fig.2 Test wind tunnel test layout

2.2 試驗(yàn)?zāi)Ｐ图皽y(cè)點(diǎn)布置

風(fēng)洞測(cè)壓剛性模型采用ABS（Acrylonitrilebutdiene-styren）板制作，滿足試驗(yàn)所需要的剛度要求，模型按幾何縮尺比例為1:20進(jìn)行設(shè)計(jì)，風(fēng)速縮尺比例設(shè)定為1:1，所以時(shí)間縮尺比例為1:20，試驗(yàn)風(fēng)速為10 m/s。模型的平面尺寸為600 mm×400 mm，屋檐高度為400 mm，屋面坡角為18.4°，房屋縮尺模型如圖3所示。本文試驗(yàn)?zāi)Ｐ偷淖枞蕿?%，滿足風(fēng)洞試驗(yàn)阻塞率小于5%的要求。屋面上采用對(duì)稱方式共布置了130個(gè)測(cè)點(diǎn)（見圖3和圖4）。為了方便研究與敘述，本研究選擇在迎風(fēng)屋面的角部、屋脊、屋檐等局部測(cè)點(diǎn)進(jìn)行區(qū)域劃分，具體分區(qū)見圖4。

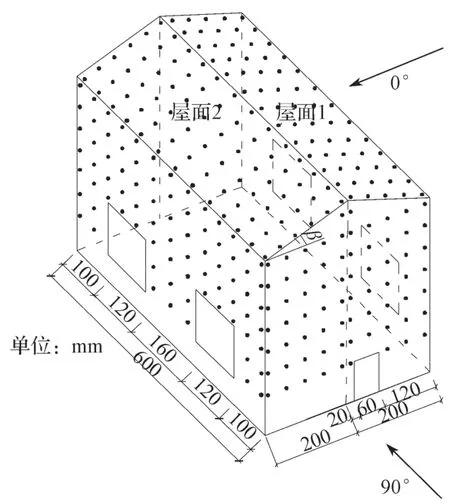
圖3 低矮房屋縮尺模型圖Fig.3 Scale model of low-rise buildings

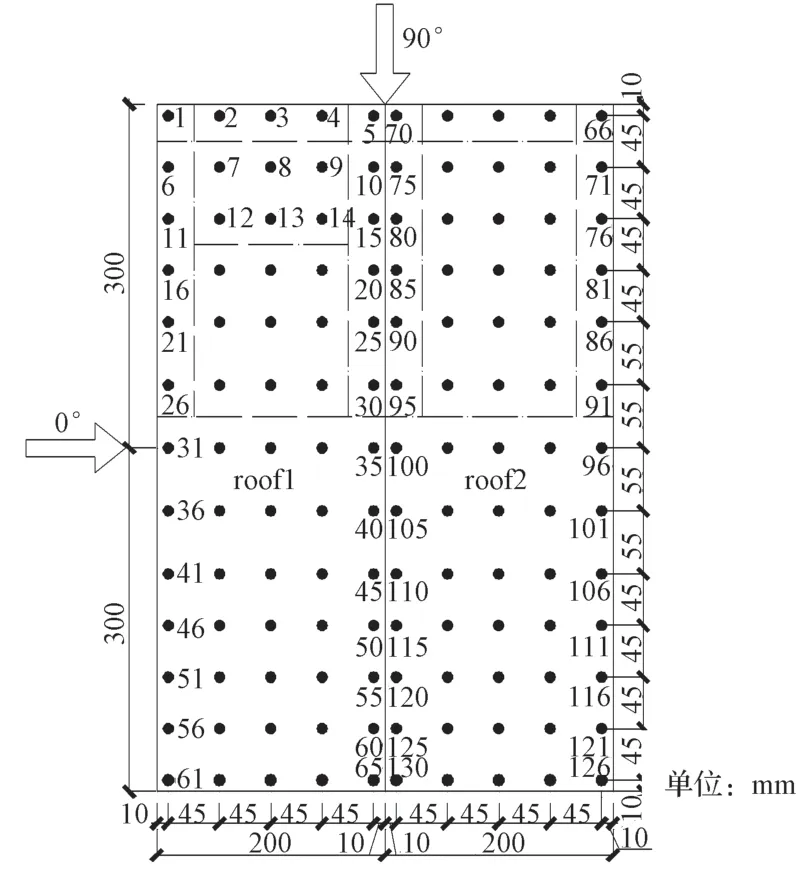
圖4 屋面測(cè)點(diǎn)布置與分區(qū)示意圖Fig.4 Layout and division diagram of roof measuring points

2.3 試驗(yàn)數(shù)據(jù)處理方法

本研究中，測(cè)壓信號(hào)的采樣頻率為332.5 Hz，采樣時(shí)間為30 s，對(duì)應(yīng)的實(shí)際建筑采樣時(shí)間為10 min，滿足GB 50009—2012《建筑結(jié)構(gòu)荷載規(guī)范》[10]中規(guī)定的不小于10 min的要求，試驗(yàn)中每個(gè)測(cè)點(diǎn)采樣個(gè)數(shù)為10 000個(gè)。風(fēng)壓系數(shù)定義為風(fēng)作用于建筑表面的實(shí)際壓力與來流風(fēng)壓的比值[11]，本文以模型屋面平均高度處風(fēng)壓作為無量綱化的參考風(fēng)壓，定義風(fēng)壓系數(shù)Cpi(t)計(jì)算式如下：

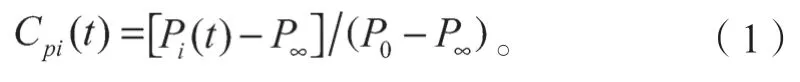
式中：Pi(t)為第i測(cè)點(diǎn)處風(fēng)壓值；

P0和P∞分別為參考高度處總壓和靜壓。

風(fēng)壓的非高斯特性通常采用風(fēng)壓系數(shù)時(shí)程的偏度和峰度來描述，二者是判別風(fēng)壓時(shí)程高斯與非高斯分布的2個(gè)重要參數(shù)。偏度值和峰度值的計(jì)算公式參考文獻(xiàn)[12]給出。

為了研究屋面特征湍流對(duì)風(fēng)壓非高斯特性的影響，可以通過分析不同測(cè)點(diǎn)間風(fēng)壓系數(shù)的互相關(guān)性進(jìn)行闡述，引入互相關(guān)系數(shù)ρxixj，定義如下：

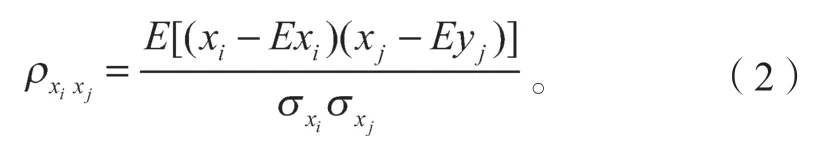
式中：xi、xj分別為測(cè)點(diǎn)i和j的風(fēng)壓系數(shù)序列；

Exi和Exj分別為xi、xj對(duì)應(yīng)的數(shù)學(xué)期望；

σxi和σxj分別為xi、xj對(duì)應(yīng)的標(biāo)準(zhǔn)差。

3 風(fēng)壓時(shí)程的概率分布

為研究屋面的風(fēng)壓概率分布特性，基于18.4°坡角屋面測(cè)點(diǎn)風(fēng)壓時(shí)程數(shù)據(jù)，本研究采用Gaussian分布、三參數(shù)Gamma分布、三參數(shù)對(duì)數(shù)正態(tài)分布、廣義極值分布（generalized extreme value distribution，GEV）4種分布方式，對(duì)屋面的典型測(cè)點(diǎn)風(fēng)壓時(shí)程進(jìn)行擬合分析。得到的B類地貌工況中45°風(fēng)向角作用下迎風(fēng)屋面的典型測(cè)點(diǎn)的風(fēng)壓系數(shù)概率密度分布擬合結(jié)果如圖5所示。

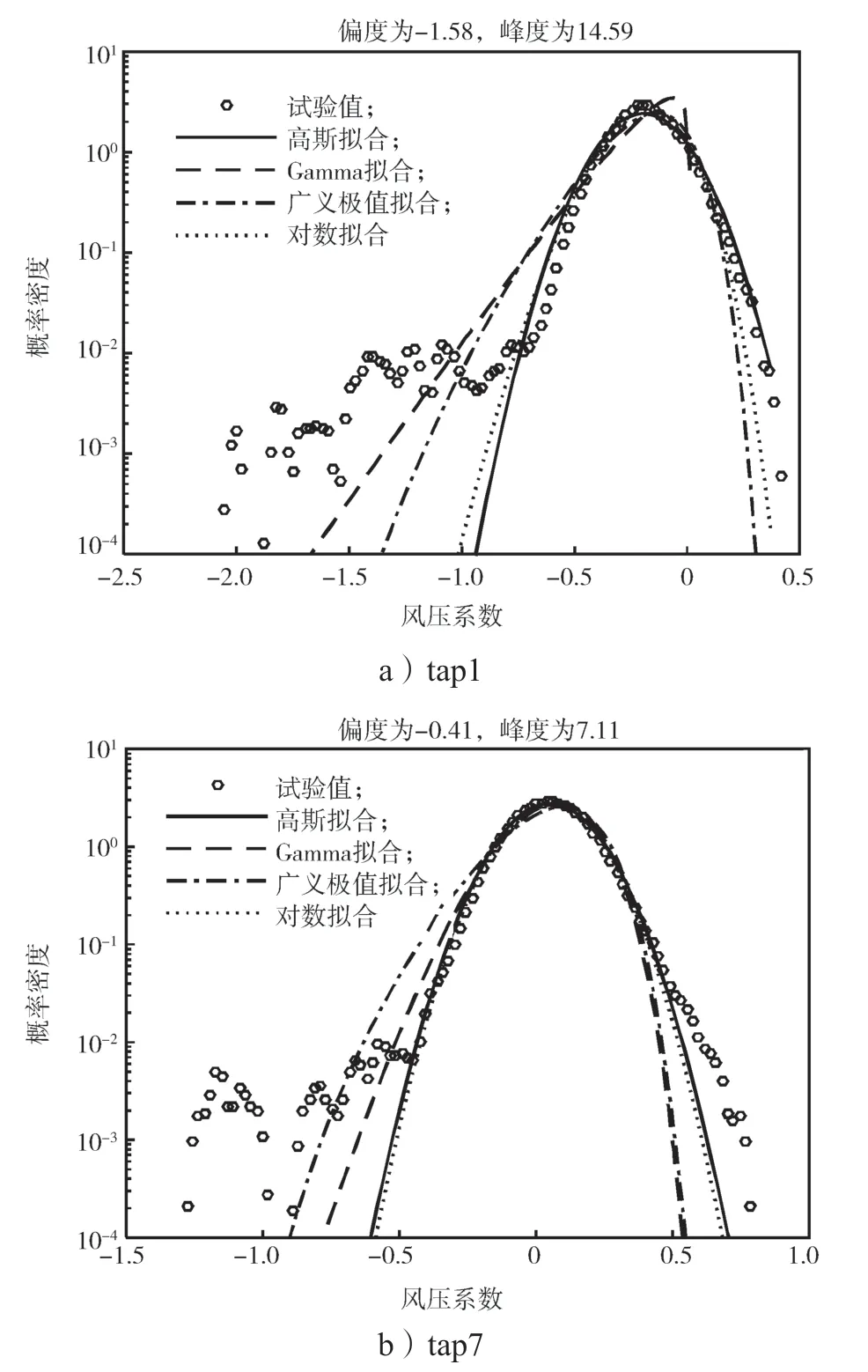
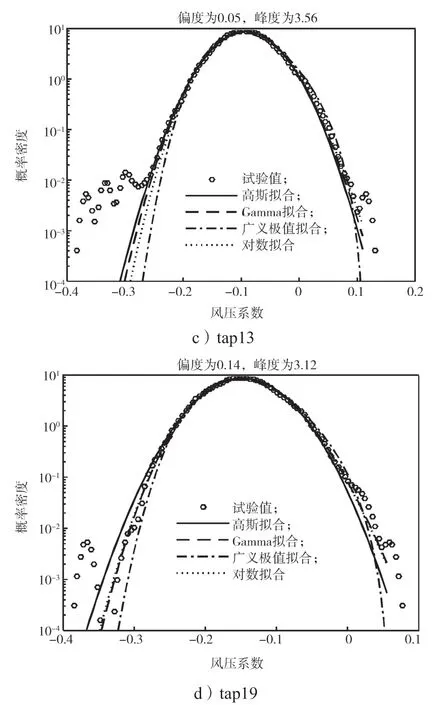
圖5 45°風(fēng)向角下迎風(fēng)屋面典型測(cè)點(diǎn)的風(fēng)壓系數(shù)概率密度曲線Fig.5 Probability density of wind pressure coefficients for typical taps on windward roof under 45°wind angle

如圖5所示，測(cè)點(diǎn)1和7處于屋蓋角部區(qū)域，風(fēng)壓系數(shù)受錐形渦影響較大，導(dǎo)致其統(tǒng)計(jì)特性偏離了高斯分布且都為負(fù)偏斜，從統(tǒng)計(jì)學(xué)上說明此區(qū)域?qū)嶋H風(fēng)吸力出現(xiàn)的概率比高斯假設(shè)更大，更易遭到破壞；其中，Gamma分布和廣義極值分布（GEV）對(duì)斜風(fēng)向角部區(qū)域測(cè)點(diǎn)風(fēng)壓時(shí)程概率分布擬合程度更高，但是對(duì)于高峰度的長(zhǎng)拖尾區(qū)域很難進(jìn)行較優(yōu)擬合。而測(cè)點(diǎn)13和19位于迎風(fēng)屋蓋中部，錐形渦發(fā)展到此區(qū)域時(shí)其截面增大，渦旋強(qiáng)度減弱[13]，因而兩者的風(fēng)壓系數(shù)概率密度分布曲線更接近高斯分布。此時(shí)測(cè)點(diǎn)13風(fēng)壓時(shí)程的偏度和峰度分別為0.05和3.56，測(cè)點(diǎn)19的分別為0.14和3.12，均接近高斯分布下的理論偏度值0和峰度值3。同時(shí)發(fā)現(xiàn)隨著與屋面角部區(qū)域距離的增加，負(fù)偏斜拖尾長(zhǎng)度減小。

4 屋面風(fēng)壓非高斯性分區(qū)

本節(jié)通過改變來流風(fēng)向角和地貌類型研究低矮雙坡建筑風(fēng)壓非高斯特性分區(qū)特點(diǎn)。理論上高斯分布的偏度與峰度值分別為0和3，但由于風(fēng)場(chǎng)紊流的隨機(jī)性導(dǎo)致實(shí)驗(yàn)過程中絕對(duì)的高斯分布很少見，因此，綜合相關(guān)研究[14-15]，文中采用|S|＞0.5且|K|＞3.5作為風(fēng)壓高斯區(qū)與非高斯區(qū)劃分的標(biāo)準(zhǔn)。

4.1 不同風(fēng)向角下非高斯性風(fēng)壓分布

通過分析B類地貌下建筑受風(fēng)向角分別為0,20,30,45,60,90°時(shí)屋面非高斯區(qū)的分布特點(diǎn)，描述風(fēng)向角對(duì)雙坡低矮建筑屋面非高斯分區(qū)的影響。B類地貌下屋面非高斯區(qū)域隨風(fēng)向角的變化分布如圖6所示，圖中實(shí)心點(diǎn)處風(fēng)壓表現(xiàn)為高斯性，而空心點(diǎn)處為非高斯性。

圖6 屋面非高斯區(qū)域隨風(fēng)向角變化分布Fig.6 Distribution of non-Gaussian area on roofs under various wind angles

由圖6可知，風(fēng)向角對(duì)非高斯區(qū)分布影響顯著，特別是斜風(fēng)向角作用下（如風(fēng)向角為20°,30°,45°,60°），高斯區(qū)分布大體與風(fēng)向角一致，如圖中箭頭所示。而非高斯區(qū)則主要分布在高斯區(qū)兩側(cè)，這是因?yàn)閬砹黠L(fēng)在經(jīng)過屋角區(qū)域后因氣流分離形成兩股錐形渦并沿著來流方向向前發(fā)展所致[16]。處于錐形渦作用范圍的測(cè)點(diǎn)受氣流渦旋影響較大而導(dǎo)致風(fēng)壓非高斯性顯著，兩股渦的中間區(qū)域風(fēng)壓由于旋渦的相互干擾反而表現(xiàn)為高斯性。

0°風(fēng)向角下，屋面大部分測(cè)點(diǎn)表現(xiàn)為非高斯性，高斯風(fēng)壓區(qū)主要集中在迎風(fēng)屋蓋第3排測(cè)點(diǎn)范圍，這是因?yàn)閬砹髦苯幼饔糜谟L(fēng)屋蓋的中部區(qū)域，而此區(qū)域受屋檐和屋脊區(qū)域的氣流分離影響較小。

90°風(fēng)向角下，非高斯區(qū)則主要分布在前后山墻區(qū)、兩側(cè)屋檐區(qū)以及屋脊區(qū)，這是由于氣流在迎風(fēng)前緣區(qū)分離產(chǎn)生旋渦脫落而在來流下游區(qū)再附所致；兩側(cè)屋檐區(qū)受建筑繞流影響較大而表現(xiàn)出明顯的非高斯性。

4.2 不同地貌下非高斯性風(fēng)壓分布

圖7～9給出了18.4°坡角雙坡低矮建筑在A、B、C 3類地貌下受來流風(fēng)向角分別為0,45,90°時(shí)的屋面非高斯區(qū)分布。

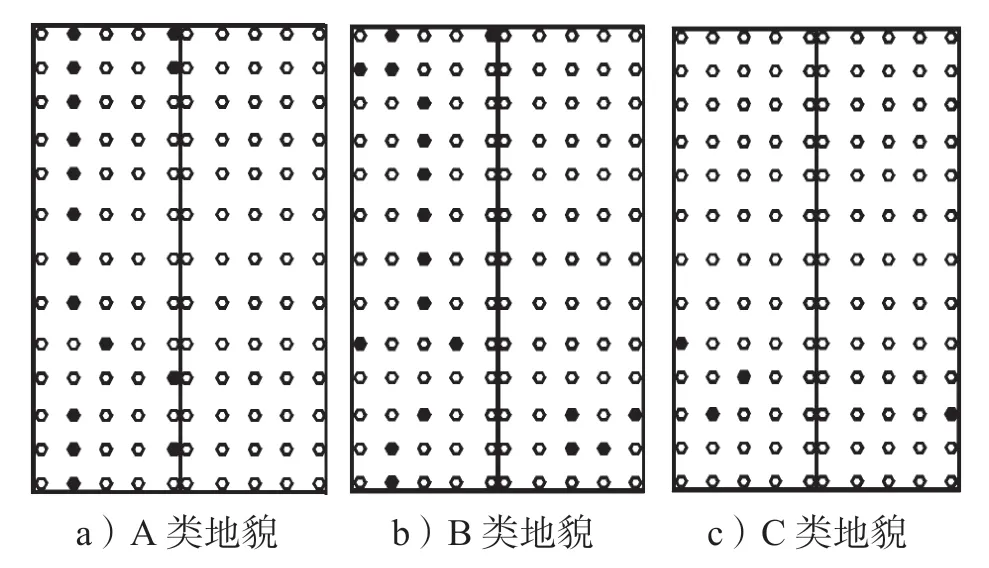
圖7 不同地貌中0°風(fēng)向角下非高斯區(qū)分布Fig.7 Distribution of non-Gaussian area under 0°wind direction angle in different landforms

圖8 不同地貌中45°風(fēng)向角下非高斯區(qū)分布Fig.8 Distribution of non-Gaussian area under 45°wind angle in different landforms

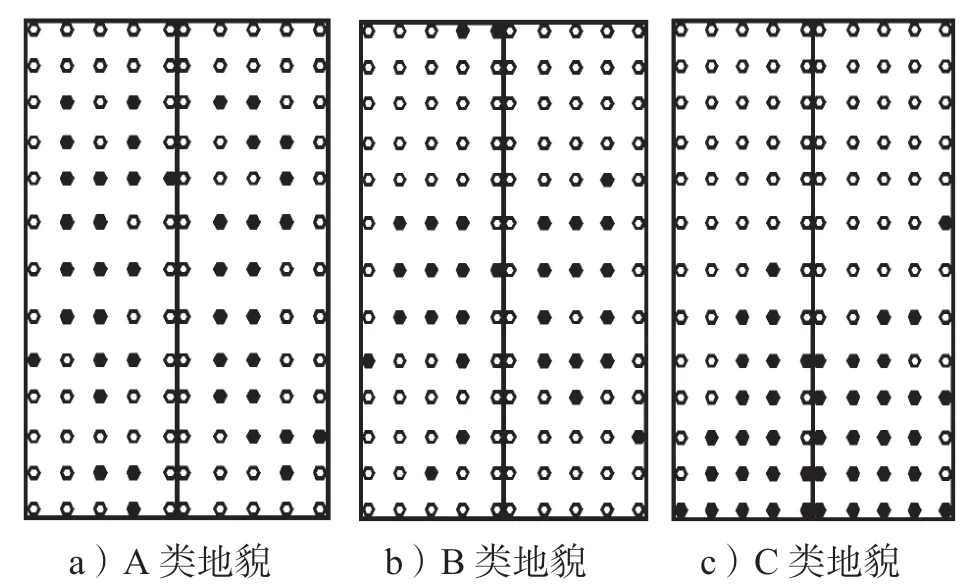
圖9 不同地貌中90°風(fēng)向角下非高斯區(qū)分布Fig.9 Distribution of non-Gaussian area under 90°wind angle in different landforms

非高斯區(qū)的分布特點(diǎn)說明了地貌類型對(duì)雙坡低矮建筑屋面非高斯區(qū)分布規(guī)律的影響，從圖7～9中可以看出，18.4°坡角的雙坡低矮建筑在相同的風(fēng)向角作用下，地貌類型對(duì)屋面非高斯區(qū)的分布影響顯著，具體描述如下。

如圖7所示，0°風(fēng)向角下，A類地貌下高斯區(qū)測(cè)點(diǎn)分布位置較B類地貌的更靠近迎風(fēng)屋檐，這是由于A類地貌中來流湍流度較小，屋檐區(qū)域處產(chǎn)生的氣流分離程度相對(duì)較小；當(dāng)建筑處于來流更為復(fù)雜的C類地貌下時(shí)，幾乎屋面所有的測(cè)點(diǎn)風(fēng)壓均表現(xiàn)為非高斯性。

如圖8所示，45°風(fēng)向角下，在A、B地貌類型中，表現(xiàn)為高斯性的測(cè)點(diǎn)主要沿來流方向按箭頭方向呈三股區(qū)域分布，結(jié)合文獻(xiàn)[17]中對(duì)斜風(fēng)向作用下低矮建筑屋面錐形渦的分布特點(diǎn)進(jìn)一步說明此結(jié)論。從A類地貌到B類地貌，三股高斯區(qū)域沿來流方向移動(dòng)，且區(qū)域范圍有所減小，這是因?yàn)樵贐類地貌中屋面錐形渦氣流影響范圍擴(kuò)大所致。

如圖9所示，90°風(fēng)向角作用下，不同地貌中兩側(cè)屋蓋非高斯測(cè)點(diǎn)區(qū)域分布基本對(duì)稱，體現(xiàn)了實(shí)驗(yàn)數(shù)據(jù)的合理性。從A類地貌到C類地貌，高斯區(qū)域沿來流方向逐漸向前移動(dòng)，這是由于隨著來流湍流度增大，在氣流分離區(qū)旋渦脫落加劇，導(dǎo)致分離區(qū)非高斯區(qū)域范圍越來越大。同時(shí)發(fā)現(xiàn)，A類地貌和B類地貌中，在屋面來流下游靠近山墻區(qū)域出現(xiàn)較大范圍的非高斯測(cè)點(diǎn)，這是由于分離氣流在此區(qū)域產(chǎn)生再附和建筑尾流的卷吸作用所致。

5 局部非高斯風(fēng)壓與屋面流場(chǎng)特性的關(guān)系

5.1 屋面風(fēng)壓非高斯性變化規(guī)律

圖10和圖11分別給出了18.4°坡角屋面，在0°風(fēng)向角作用下，順風(fēng)向測(cè)點(diǎn)風(fēng)壓偏度變化曲線和峰度變化曲線。

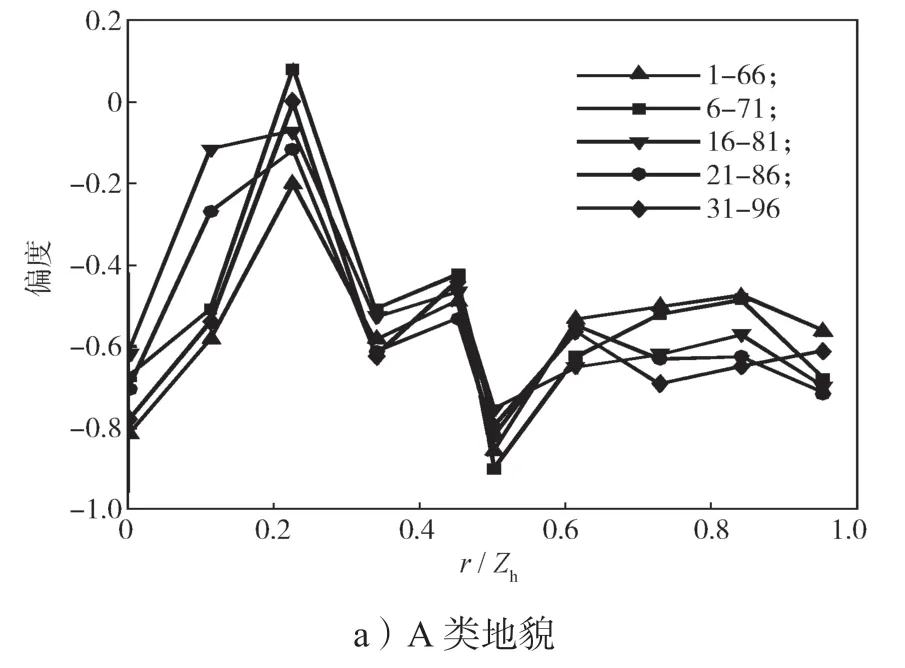
圖10 不同地貌中0°風(fēng)向角作用下順風(fēng)向測(cè)點(diǎn)風(fēng)壓偏度變化曲線Fig.10 Curves of skewness change under a wind direction angle of 0°

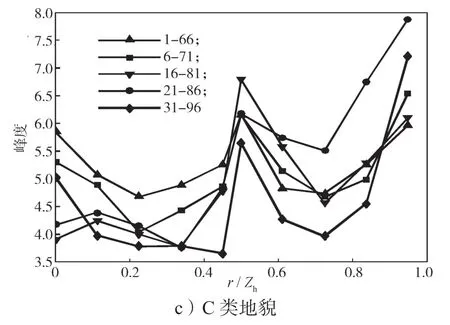
圖11 不同地貌中0°風(fēng)向角作用下順風(fēng)向測(cè)點(diǎn)風(fēng)壓峰度變化曲線Fig.11 Curves of kurtosis change under a wind direction angle of 0°

圖10和11中各曲線圖標(biāo)分別代表相關(guān)性計(jì)算參考點(diǎn)和所考察目標(biāo)測(cè)點(diǎn)序列的最后點(diǎn)，橫坐標(biāo)表示屋面測(cè)點(diǎn)距離與屋檐高度的比值，圖12、13同。

從圖10所示不同地貌中0°風(fēng)向角作用下順風(fēng)向測(cè)點(diǎn)風(fēng)壓偏度曲線和圖11所示不同地貌中0°風(fēng)向角作用下順風(fēng)向測(cè)點(diǎn)風(fēng)壓峰度變化曲線的變化趨勢(shì)來看，不同地貌下偏度的變化趨勢(shì)大體一致呈“M”形，且整體呈現(xiàn)出下降的態(tài)勢(shì)；而峰度曲線則呈現(xiàn)出“W”形的變化趨勢(shì)，且整體呈上升趨勢(shì)。這一結(jié)果，一方面說明偏度與峰度一般表現(xiàn)為明顯的不同步性；另一方面，說明小偏斜高峰態(tài)以及大偏斜低峰態(tài)出現(xiàn)的概率較低。從偏度極值與峰度極值出現(xiàn)的位置來看，不同地貌類型下，迎風(fēng)屋面約0.2倍屋檐高度處的風(fēng)壓偏度和峰度均出現(xiàn)了較明顯的極值點(diǎn)，表現(xiàn)為極小偏度（絕對(duì)值）和峰度，非高斯性最弱；在屋脊位置（0.5倍屋檐高度）附近，風(fēng)壓偏度和峰度大多出現(xiàn)了第二個(gè)明顯的極值點(diǎn)，表現(xiàn)為較大的偏度（絕對(duì)值）和峰度，非高斯性顯著增強(qiáng)，但是C類地貌中偏度的極大值（絕對(duì)值）點(diǎn)出現(xiàn)在0.6倍屋檐高度處（即背風(fēng)屋脊處），這不排除是實(shí)驗(yàn)誤差所致。另外，發(fā)現(xiàn)屋面的第4排、第5排測(cè)點(diǎn)（迎風(fēng)屋面靠近屋脊的兩排測(cè)點(diǎn)）的風(fēng)壓偏度值，在C類地貌中沒有出現(xiàn)類似于A、B類地貌中先下降后上升的變化過程，而是表現(xiàn)為平緩地下降。

5.2 屋面流場(chǎng)特性的相關(guān)性分析

本節(jié)將從風(fēng)壓空間相關(guān)性著手分析屋面風(fēng)壓非高斯特性的分布規(guī)律，已有的相關(guān)研究結(jié)果表明，產(chǎn)生大尺度旋渦的區(qū)域一般表現(xiàn)為風(fēng)壓空間相關(guān)性較強(qiáng)[15]，互相關(guān)性系數(shù)可以用于衡量任意兩個(gè)測(cè)點(diǎn)在一定時(shí)間序列下取值的相關(guān)性程度，統(tǒng)計(jì)學(xué)上通常認(rèn)為相關(guān)系數(shù)絕對(duì)值大于0.5時(shí)兩者為強(qiáng)相關(guān)，而當(dāng)相關(guān)性系數(shù)絕對(duì)值小于0.2時(shí)，則視為弱相關(guān)。0°風(fēng)向角下，順風(fēng)向測(cè)點(diǎn)風(fēng)壓空間相關(guān)性曲線如圖12所示，0°風(fēng)向角下橫風(fēng)向測(cè)點(diǎn)的風(fēng)壓空間相關(guān)性曲線如圖13所示。

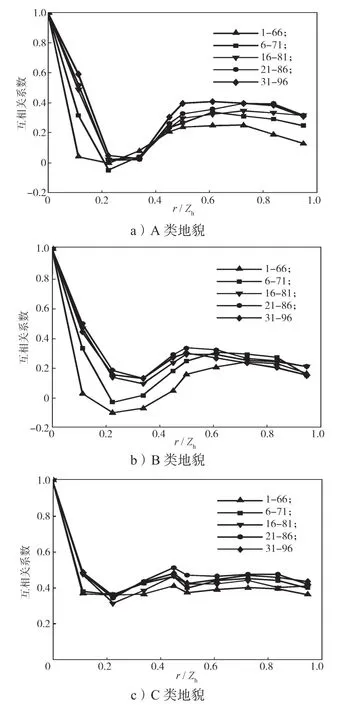
圖12 0°風(fēng)向角下順風(fēng)向測(cè)點(diǎn)風(fēng)壓空間相關(guān)性曲線Fig.12 Curves of wind spatial correlation of downwind direction point under a wind direction of 0°

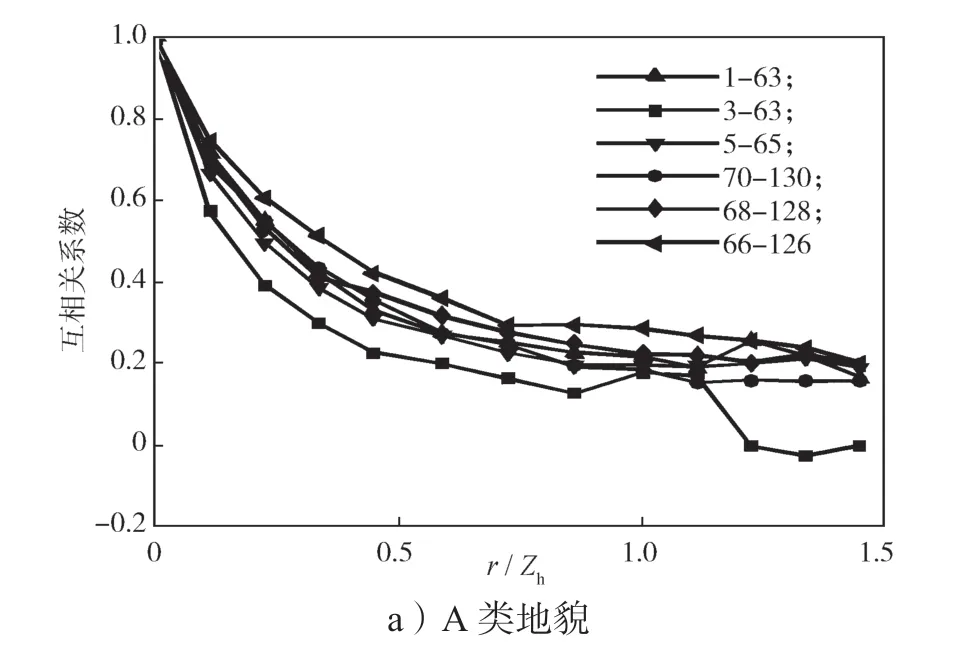
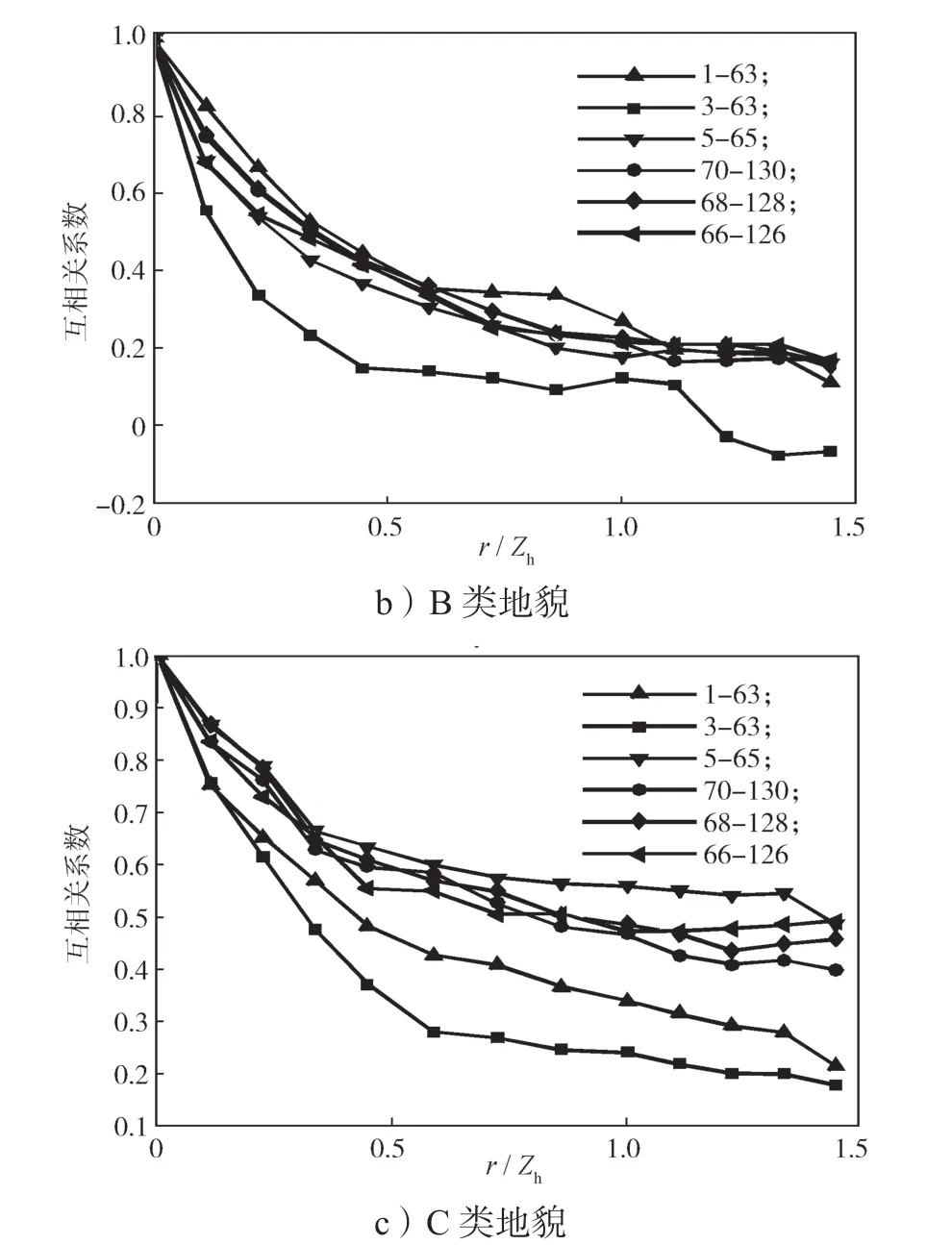
圖13 0°風(fēng)向角下橫風(fēng)向測(cè)點(diǎn)風(fēng)壓空間相關(guān)性曲線Fig.13 Curves of wind spatial correlation of cross wind points under a wind direction of 0°

圖12和13僅給出了0°風(fēng)向角下的測(cè)點(diǎn)風(fēng)壓空間相關(guān)性結(jié)果，由圖可知，屋面受0°風(fēng)向角作用時(shí)，不同地貌下順風(fēng)向和橫風(fēng)向各列測(cè)點(diǎn)風(fēng)壓相關(guān)系數(shù)的變化趨勢(shì)基本一致。由圖10可知，迎風(fēng)前緣區(qū)測(cè)點(diǎn)風(fēng)壓的相關(guān)性最強(qiáng)，風(fēng)壓非高斯性最強(qiáng)，在約0.2倍屋檐高度處風(fēng)壓相關(guān)性達(dá)到最弱相關(guān)，之后測(cè)點(diǎn)風(fēng)壓相關(guān)性增大，在屋脊區(qū)域附近達(dá)到另一個(gè)峰值，背風(fēng)屋蓋區(qū)測(cè)點(diǎn)風(fēng)壓相關(guān)性相比于屋脊略有衰減。由圖13可知，橫風(fēng)向相關(guān)性曲線基本符合負(fù)指數(shù)率模型，與順風(fēng)向風(fēng)壓相關(guān)性曲線的差別較大；不同地貌下位于約0.2倍屋檐高度處的3～63測(cè)點(diǎn)序列相關(guān)性最弱，結(jié)合橫風(fēng)向測(cè)點(diǎn)相關(guān)性規(guī)律，說明屋面上約0.2倍屋檐高度處受特征湍流[18]的影響最小，非高斯特性最弱。同時(shí)結(jié)合圖10和11可以看出，C類地貌下各測(cè)點(diǎn)序列相關(guān)性明顯較其他兩類地貌下的強(qiáng)，這是由于C類地貌下來流風(fēng)脈動(dòng)性更強(qiáng)，導(dǎo)致屋面測(cè)點(diǎn)間的風(fēng)壓相關(guān)性增強(qiáng)。

綜合上述分析，發(fā)現(xiàn)風(fēng)壓相關(guān)性曲線波動(dòng)與偏度和峰度變化趨勢(shì)具有明顯的關(guān)聯(lián)規(guī)律：風(fēng)壓相關(guān)性較弱的區(qū)域偏度和峰度都較小，而風(fēng)壓相關(guān)性較強(qiáng)的區(qū)域偏度和峰度較大。這一結(jié)論說明屋面風(fēng)壓非高斯性與屋面氣流的相互作用呈正相關(guān)，這與文獻(xiàn)[12]中的結(jié)論一致。通過分析屋面測(cè)點(diǎn)風(fēng)壓的相關(guān)性，可以了解典型雙坡屋面風(fēng)壓的非高斯性分布特點(diǎn)。

6 結(jié)論

通過對(duì)坡角為18.4°的典型雙坡低矮建筑在不同地貌下進(jìn)行風(fēng)洞試驗(yàn)，并對(duì)屋面典型測(cè)點(diǎn)風(fēng)壓時(shí)程進(jìn)行概率密度擬合，分析屋面非高斯風(fēng)壓區(qū)分布特點(diǎn)及屋面局部風(fēng)壓非高斯特性與屋面流場(chǎng)的關(guān)系，得出如下結(jié)論：

1）斜風(fēng)向作用下，風(fēng)壓非高斯特性顯著，而對(duì)于距迎風(fēng)角部較遠(yuǎn)的測(cè)點(diǎn)風(fēng)壓更加接近高斯分布。斜風(fēng)向下Gamma分布和廣義極值分布（GEV）對(duì)迎風(fēng)角部測(cè)點(diǎn)風(fēng)壓時(shí)程概率分布擬合效果更優(yōu)，但是對(duì)于高峰度的長(zhǎng)拖尾區(qū)域仍很難進(jìn)行較優(yōu)擬合。

2）高斯區(qū)測(cè)點(diǎn)分布隨風(fēng)向角的改變而變化，非高斯性測(cè)點(diǎn)由于受錐形渦外圍影響而分布在其兩側(cè)；0°風(fēng)向角下，高斯區(qū)主要分布在垂直來流方向第3排測(cè)點(diǎn)；90°風(fēng)向角下，非高斯區(qū)分布于迎風(fēng)山墻的氣流分離區(qū)和背風(fēng)山墻氣流再附區(qū)。

3）0°風(fēng)向角下，隨著來流湍流強(qiáng)度的增大，高斯區(qū)分布沿來流方向前移；45°風(fēng)向角下，A、B兩類地貌中高斯性測(cè)點(diǎn)主要沿來流方向分成三股區(qū)域，且由A類地貌變化到B類地貌時(shí)，該高斯區(qū)域沿來流方向發(fā)生移動(dòng)，且區(qū)域范圍縮小。

4）不同地貌下，偏度變化大體呈“M”形變化趨勢(shì)，整體呈下降態(tài)勢(shì)；而峰度呈“W”形變化趨勢(shì)，整體呈上升趨勢(shì)，偏度與峰度具有明顯的不同步性。風(fēng)壓相關(guān)性曲線波動(dòng)與偏度和峰度變化趨勢(shì)具有明顯的相關(guān)聯(lián)規(guī)律，相關(guān)系數(shù)大的區(qū)域，風(fēng)壓的非高斯特性更顯著。