基于分?jǐn)?shù)階灰色模型的農(nóng)業(yè)用水量預(yù)測

李 俊，宋松柏，郭田麗，王小軍

基于分?jǐn)?shù)階灰色模型的農(nóng)業(yè)用水量預(yù)測

李 俊1，宋松柏1※，郭田麗1，王小軍2,3

（1. 西北農(nóng)林科技大學(xué)水利與建筑工程學(xué)院，楊凌 712100；2. 南京水利科學(xué)研究院水文水資源研究所，南京 210029；3. 水利部應(yīng)對氣候變化研究中心，南京 210029）

針對農(nóng)業(yè)用水量序列的振蕩特性以及傳統(tǒng)灰色預(yù)測模型的過擬合問題，該文提出分?jǐn)?shù)階灰色預(yù)測模型。將農(nóng)業(yè)用水量振蕩序列轉(zhuǎn)化為單調(diào)遞減非負(fù)序列，并以轉(zhuǎn)化序列為基礎(chǔ)，根據(jù)“階數(shù)最大（或最小）”、“歷史數(shù)據(jù)擬合最好”2個目標(biāo)函數(shù)構(gòu)造優(yōu)化模型，采用改進(jìn)NSGA-II（non-dominated sorting genetic algorithm II，NSGA-II）進(jìn)行模型求解。根據(jù)驗證集擬合結(jié)果優(yōu)選出模型階數(shù)，結(jié)合分?jǐn)?shù)階反向累加灰色模型（fractional order reverse accumulation grey model），以通遼市和寶雞市為例，進(jìn)行農(nóng)業(yè)用水量的預(yù)測。為了檢驗?zāi)Ｐ托阅埽瑢⒃撐哪Ｐ头謩e與傳統(tǒng)GM(1,1)模型、自回歸模型、基于小波分析理論組合模型進(jìn)行對比。結(jié)果表明，該文模型對于通遼市、寶雞市與鄂爾多斯市的農(nóng)業(yè)用水量預(yù)測的相對誤差分別為2.33%、0.31%和1.77%。同時，該文模型預(yù)測誤差最小(比自回歸模型分別低1.11%(通遼)、6.18%（寶雞）；比傳統(tǒng)GM(1,1)模型分別低3.32%(通遼)、0.97%（寶雞）)，具有一定實用性，研究結(jié)果可為區(qū)域農(nóng)業(yè)用水量預(yù)測提供依據(jù)。

農(nóng)業(yè)；水；模型；分?jǐn)?shù)階；灰色預(yù)測；振蕩序列；過擬合；多目標(biāo)優(yōu)化

0 引 言

水資源優(yōu)化配置是實現(xiàn)水資源可持續(xù)利用的重要手段[1]。準(zhǔn)確預(yù)測通遼市、寶雞市用水量是發(fā)揮該地區(qū)水資源優(yōu)化配置效用的關(guān)鍵[2]。在區(qū)域（通遼市、寶雞市）用水戶中，農(nóng)業(yè)用水量占總用水量的70%以上[3]，因此，農(nóng)業(yè)用水量預(yù)測對于區(qū)域用水量預(yù)測具有重要的科學(xué)意義。

目前，農(nóng)業(yè)用水量預(yù)測的方法主要有定額法[4]、BP神經(jīng)網(wǎng)絡(luò)法[5]、自回歸滑動平均模型（autoregressive moving average model，ARMA）[6]、指數(shù)模型法[7]、灰色模型法[8-9]和系統(tǒng)動力學(xué)法[10]等200多種預(yù)測方法，其中常用方法有20～30種[11]。定額法主要依據(jù)作物特點與現(xiàn)行灌水定額進(jìn)行預(yù)測，但灌水定額編制具有一定主觀性與不確定性，因此，定額法難以實現(xiàn)精確預(yù)測[12]。神經(jīng)網(wǎng)絡(luò)法需要大量的數(shù)據(jù)進(jìn)行模型訓(xùn)練，同時還存在過擬合的問題[13-14]。ARMA模型與自回歸模型對數(shù)據(jù)的平穩(wěn)性要求較高[15]。由于實際用水量序列并不完全符合指數(shù)關(guān)系，這也限制了指數(shù)模型法的應(yīng)用范圍[16]。系統(tǒng)動力學(xué)方法需要的數(shù)據(jù)多、工作量大，而且對實際操作人員的要求高，影響了該方法的進(jìn)一步推廣[16]。灰色模型是一種研究“貧信息”、“小樣本”和不確定性問題的方法[17]，被廣泛應(yīng)用于經(jīng)濟、金融等領(lǐng)域。年農(nóng)業(yè)用水量的歷史數(shù)據(jù)量不大，同時受到多種因素的影響，具有震蕩性，因此采用灰色模型對農(nóng)業(yè)用水量進(jìn)行預(yù)測具有一定適用性。

分?jǐn)?shù)階灰色模型將模型階數(shù)從正整數(shù)擴展為正實數(shù)，能夠有效地提高灰色模型的預(yù)測精度[18]。在分?jǐn)?shù)階灰色模型中，分?jǐn)?shù)階反向累加灰色模型相對于傳統(tǒng)的GM(1,1)模型具有預(yù)測擾動小、能夠利用序列新信息等特點，受到許多學(xué)者關(guān)注[19]。雖然分?jǐn)?shù)階反向累加灰色模型在某些情況下也適用于單調(diào)非負(fù)遞增數(shù)列[20]，但主要是針對單調(diào)非負(fù)遞減序列[21]，同時，實際的歷史用水?dāng)?shù)據(jù)具有一定的振蕩性。針對這些問題，需要將歷史用水?dāng)?shù)據(jù)轉(zhuǎn)化為單調(diào)非負(fù)遞減序列，文獻(xiàn)[22-24]提出將振蕩序列轉(zhuǎn)化為單調(diào)非負(fù)遞增序列的方法。為了適應(yīng)分?jǐn)?shù)階反向累加灰色模型對于單調(diào)非負(fù)遞減序列的要求，本文提出將振蕩序列轉(zhuǎn)化為單調(diào)非負(fù)遞減序列的方法，并以轉(zhuǎn)化后的數(shù)據(jù)為基礎(chǔ)，建立分?jǐn)?shù)階反向累加GM(1,1)模型，進(jìn)行未來農(nóng)業(yè)用水量預(yù)測。

分?jǐn)?shù)階反向累加灰色模型的階數(shù)對于模型預(yù)測效果有較大影響，以往階數(shù)的確定大多以“歷史數(shù)據(jù)擬合最好”為目標(biāo)函數(shù)構(gòu)造優(yōu)化模型，使用智能優(yōu)化算法對模型求解，并求得最終階數(shù)[20,25-27]。這種方法僅以歷史數(shù)據(jù)擬合程度作為目標(biāo)函數(shù)，往往會造成過擬合，使模型對歷史數(shù)據(jù)中的噪聲過度學(xué)習(xí)。為解決這一問題，本文采用“階數(shù)最大（或最小）”、“歷史數(shù)據(jù)擬合最好”2個目標(biāo)函數(shù)來構(gòu)造多目標(biāo)優(yōu)化模型，應(yīng)用Matlab編程，采用改進(jìn)多目標(biāo)遺傳算法（改進(jìn)NSGA-II）對優(yōu)化模型進(jìn)行求解，獲得最優(yōu)階數(shù)，構(gòu)建分?jǐn)?shù)階反向累加GM(1,1)模型。在此基礎(chǔ)上，選用內(nèi)蒙古自治區(qū)通遼市和陜西省寶雞市為研究區(qū)，進(jìn)行農(nóng)業(yè)用水量預(yù)測。通過本文研究，以期為中國農(nóng)業(yè)需水量預(yù)測研究提供新的研究手段和支撐。

1 改進(jìn)分?jǐn)?shù)階灰色預(yù)測模型

1.1 數(shù)據(jù)預(yù)處理

將收集到的歷史數(shù)據(jù)劃分為訓(xùn)練數(shù)據(jù)、驗證數(shù)據(jù)和測試數(shù)據(jù)3種。由于歷史用水序列為振蕩序列，需要將訓(xùn)練數(shù)據(jù)集、驗證數(shù)據(jù)集轉(zhuǎn)換為單調(diào)非負(fù)序列。

設(shè)訓(xùn)練數(shù)據(jù)集、驗證數(shù)據(jù)集組成的有序序列為（1、2、…x、x1…x），其中，前個為訓(xùn)練數(shù)據(jù)，為訓(xùn)練數(shù)據(jù)集、驗證數(shù)據(jù)集數(shù)據(jù)的總量，記=max（x-x1|=1、2…），則通過式（1）可將振蕩序列轉(zhuǎn)化為單調(diào)非負(fù)遞減序列；

y=x-（-1）+│x-（-1）│+1（1）

式中y（=1、2…）為轉(zhuǎn)換后單調(diào)非負(fù)遞減的訓(xùn)練數(shù)據(jù)序列。

1.2 分?jǐn)?shù)階反向累加GM(1,1)模型

分?jǐn)?shù)階反向累加GM(1,1)模型相對于傳統(tǒng)的GM(1,1)模型具有預(yù)測擾動小，能夠利用新信息的優(yōu)點。根據(jù)分?jǐn)?shù)階反向累加灰色模型原理，階反向累加算子可寫為[18]

模型的時間響應(yīng)式為

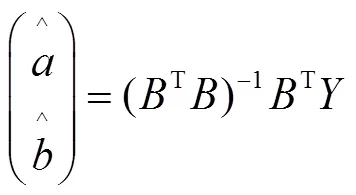
1.3 模型最優(yōu)階數(shù)確定方法

1.3.1 基于歷史數(shù)據(jù)擬合確定最優(yōu)階數(shù)

以歷史數(shù)據(jù)擬合最優(yōu)為目標(biāo)函數(shù)，可挖掘歷史數(shù)據(jù)的內(nèi)在規(guī)律，為將來的預(yù)測奠定基礎(chǔ)[25-27]，具體見式（5），但需要指出的是，過度依賴該式也會存在過擬合的風(fēng)險。

式中2()表示模型對歷史數(shù)據(jù)擬合的程度。

1.3.2 最優(yōu)階數(shù)確定方法的改進(jìn)

為了克服計算模型過擬合問題，本文選用“階數(shù)最大（或最小）”為目標(biāo)函數(shù)。同時結(jié)合式（5），構(gòu)造多目標(biāo)優(yōu)化模型。

1()表示最大（或最小）階數(shù)。對于式（6），僅以式（5）為目標(biāo)函數(shù)尋找模型階數(shù)會造成模型過擬合，因此，需要防止模型的過度學(xué)習(xí)，即防止對歷史數(shù)據(jù)的過度擬合。而歷史數(shù)據(jù)擬合效果與模型階數(shù)在不同區(qū)間會呈現(xiàn)出正相關(guān)或負(fù)相關(guān)關(guān)系。當(dāng)兩者呈現(xiàn)正相關(guān)時，為了防止過擬合，需要減小階數(shù)以降低歷史數(shù)據(jù)擬合效果，即以階數(shù)最小為目標(biāo)；而兩者呈現(xiàn)負(fù)相關(guān)時，則需要加大階數(shù)，即以階數(shù)最大為目標(biāo)，因此，需要將式（6）的2種形式均進(jìn)行試算，從而求出最優(yōu)階數(shù)。

應(yīng)用改進(jìn)的NSGA-II對式（5）～（6）組成的優(yōu)化模型進(jìn)行求解，得到1個帕累托解集，將解集中的各階數(shù)代入分?jǐn)?shù)階反向累加GM(1,1)模型，對驗證數(shù)據(jù)集中的數(shù)據(jù)預(yù)測，按照式（7）評價模擬效果，選出模擬效果最好的階數(shù)作為模型最終階數(shù)。

式中3()表示模型對驗證集數(shù)據(jù)預(yù)測的相對誤差。

根據(jù)求得的最終階數(shù)，結(jié)合分?jǐn)?shù)階反向累加GM(1,1)模型對測試數(shù)據(jù)集的數(shù)據(jù)進(jìn)行預(yù)測。

2 案例分析

2.1 研究區(qū)概況

本文選取內(nèi)蒙古自治區(qū)通遼市（42°15′～45°59′N，119°14′～123°43′E）和陜西省寶雞市（33°35′～35°06′N，106°18′～108°03′E）為研究區(qū)域（見圖1），農(nóng)業(yè)分別為2市的主要用水戶，占總用水量的70%以上，農(nóng)業(yè)用水效率均在50%左右。2市分別為內(nèi)蒙古自治區(qū)和陜西省糧食生產(chǎn)的主要基地之一[29-30]，隨著社會經(jīng)濟的發(fā)展，其他行業(yè)用水?dāng)D占了農(nóng)業(yè)用水，水污染日益嚴(yán)重，2市的農(nóng)業(yè)供水壓力加大。因此，有必要對2市的農(nóng)業(yè)用水進(jìn)行預(yù)測，以期為農(nóng)業(yè)供水統(tǒng)籌規(guī)劃提供依據(jù)。根據(jù)《2007—2017年內(nèi)蒙古自治區(qū)水資源公報》、《2007—2017年陜西省水資源公報》，收集通遼市和寶雞市2007—2017年農(nóng)業(yè)用水量數(shù)據(jù)，參考文獻(xiàn)[31-33]，按照6∶2∶2的比例設(shè)置為訓(xùn)練數(shù)據(jù)、驗證數(shù)據(jù)和測試數(shù)據(jù)。研究區(qū)農(nóng)業(yè)用水量見圖2。

文獻(xiàn)[22-24,34-35]提出，存在，∈（2,3,…）使x>x-1，x<x-1，則稱有序序列（1、2、…x、x1…x）為振蕩（波動）序列。按照振蕩（波動）序列的定義，從圖2可以看出，通遼市和寶雞市的農(nóng)業(yè)用水量呈現(xiàn)一定的波動性（如通遼市2007年農(nóng)業(yè)用水量大于2008年農(nóng)業(yè)用水量，而2008年農(nóng)業(yè)用水量小于2009年農(nóng)業(yè)用水量，寶雞市2007年農(nóng)業(yè)用水量小于2008年農(nóng)業(yè)用水量，而2008年農(nóng)業(yè)用水量大于2009年農(nóng)業(yè)用水量）。

圖2 轉(zhuǎn)化后的數(shù)據(jù)與原始數(shù)據(jù)對比

2.2 模型應(yīng)用及結(jié)果分析

2.2.1 數(shù)據(jù)預(yù)處理結(jié)果分析

為了使得訓(xùn)練數(shù)據(jù)適應(yīng)分?jǐn)?shù)階反向累加灰色模型對于數(shù)據(jù)“平穩(wěn)、單調(diào)遞減、非負(fù)”的要求，需要去除數(shù)據(jù)的波動性，轉(zhuǎn)化為單調(diào)遞減的非負(fù)序列。按照式（1）進(jìn)行數(shù)據(jù)轉(zhuǎn)化，轉(zhuǎn)化后的數(shù)據(jù)與原始數(shù)據(jù)的對比見圖2，轉(zhuǎn)化結(jié)果見圖2。

由圖2可以看出，轉(zhuǎn)化后的數(shù)據(jù)為單調(diào)遞減序列，按照振蕩（波動）序列的定義，轉(zhuǎn)化后的序列不屬于振蕩序列，說明本文的轉(zhuǎn)化方法很好地去除數(shù)據(jù)的波動性。經(jīng)過轉(zhuǎn)化后，使數(shù)據(jù)呈現(xiàn)單調(diào)遞減的趨勢，并且保持非負(fù)的特性，符合分?jǐn)?shù)階反向累加模型對于基礎(chǔ)數(shù)據(jù)的要求。因此，數(shù)據(jù)轉(zhuǎn)化后在擴大模型適用范圍、提供模型較為合適的基礎(chǔ)數(shù)據(jù)等方面具有積極的作用。同時，最終預(yù)測結(jié)果需要逆向還原計算，消除轉(zhuǎn)化方式對模型的影響。

轉(zhuǎn)化后的數(shù)據(jù)符合“非負(fù)”和“單調(diào)遞減”的特性，可作為分?jǐn)?shù)階反向累加模型的訓(xùn)練與驗證數(shù)據(jù)集。

2.2.2 最優(yōu)階數(shù)確定

為了確定最優(yōu)階數(shù)，先以“階數(shù)最小”與“歷史數(shù)據(jù)擬合最好”為目標(biāo)函數(shù)構(gòu)造關(guān)于階數(shù)的多目標(biāo)優(yōu)化模型，并使用改進(jìn)的NSGA-II對模型求解，求得帕累托前端。同樣，以“階數(shù)最大”與“歷史數(shù)據(jù)擬合最好”為目標(biāo)函數(shù)構(gòu)造關(guān)于階數(shù)的多目標(biāo)優(yōu)化模型，并使用改進(jìn)的NSGA-II對模型進(jìn)行求解，求得帕累托前端，見圖3。從圖3可以看出，解集都為帕累托解集，說明改進(jìn)的NSGA-II具有較好求解效果。目前關(guān)于遺傳算法參數(shù)選擇問題并無統(tǒng)一的解決方法，主要通過全面試驗法等方法進(jìn)行確定[36]，本文參考文獻(xiàn)[37]的方法，通過數(shù)值模擬試驗，確定NSGA-II的參數(shù)。NSGA-II種群大小為1 000，進(jìn)化代數(shù)為200代，最優(yōu)前端個體系數(shù)為0.3，停止代數(shù)200，適應(yīng)度函數(shù)偏差為e-1 000。

圖3 農(nóng)業(yè)用水量模型最優(yōu)階數(shù)確定帕累托解集

將帕累托前端中的階數(shù)逐個代入分?jǐn)?shù)階反向累加GM(1,1)模型，進(jìn)行驗證數(shù)據(jù)集數(shù)據(jù)模擬，并根據(jù)式（7）確定模型階數(shù)，驗證集預(yù)測誤差見圖4。由圖4可以得出，階數(shù)為0.976 1、0.006 2時，模型對于驗證數(shù)據(jù)集中數(shù)據(jù)的預(yù)測效果最好。因此，分別選定0.976 1、0.006 2為通遼市、寶雞市預(yù)測模型的最終階數(shù)。

2.2.3 模型比較與檢驗

為了對本文所提出模型的性能進(jìn)行檢驗，將本文模型與傳統(tǒng)GM(1,1)模型[38]、自回歸模型[39]進(jìn)行對比，其中各個模型對于測試集的預(yù)測效果見表1。

圖4 各個階數(shù)的預(yù)測誤差

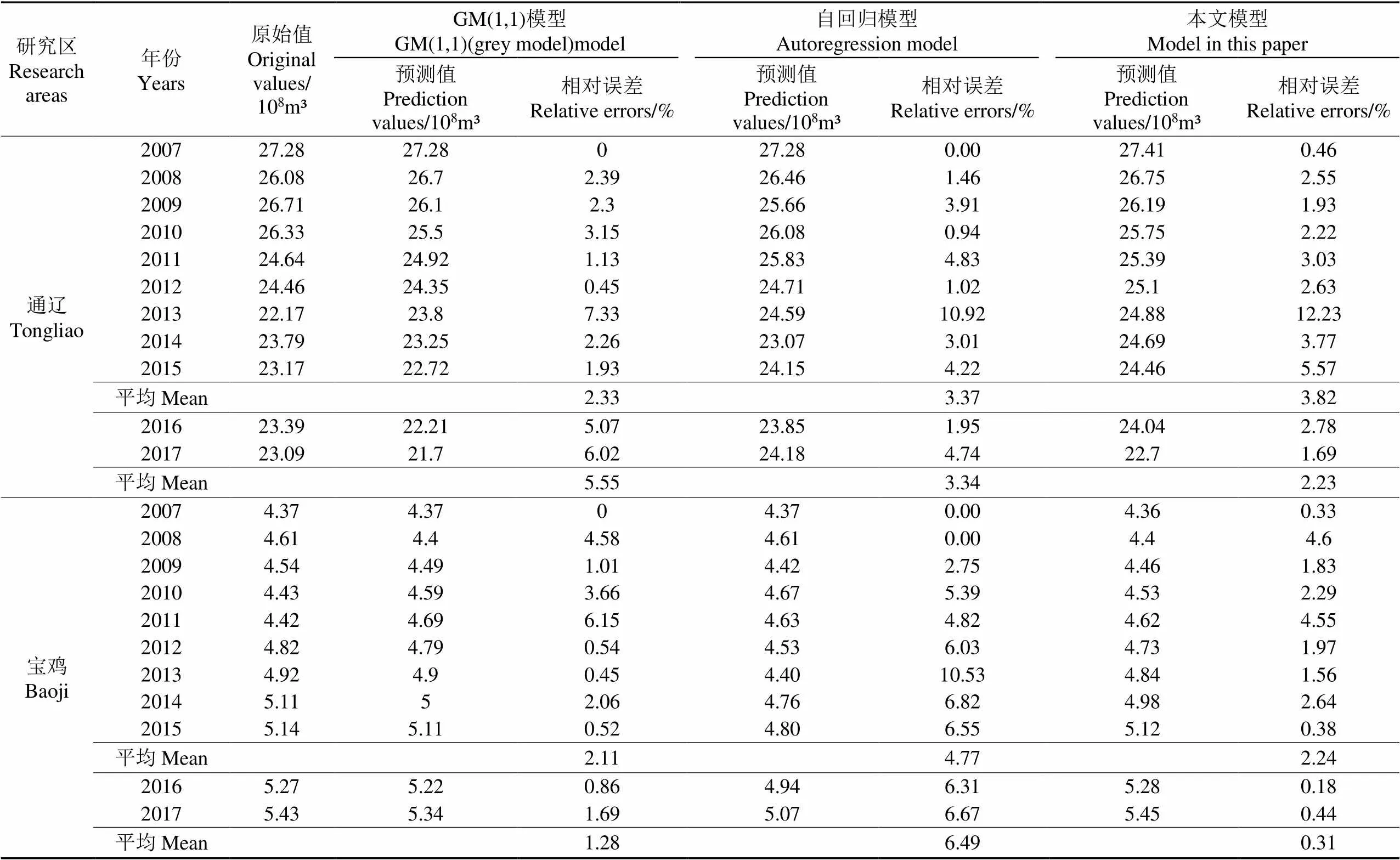
表1 各個模型預(yù)測效果對比

注：2016和2017年為測試集，其他年份為非測試集，用于模型率定。

Note: 2016 and 2017 belong to the test set, and other years belong to the non-test set for model parameters determination.

從表1可以看出本文模型對于通遼市和寶雞市測試集用水量的平均預(yù)測誤差分別為2.23%、0.31%，誤差較小，說明本文模型具有較好的泛化能力。

由表1還可以看出，對于非測試集的模擬，GM(1,1)模型具有最好的模擬效果，相對誤差為2.33%（通遼）、2.11%（寶雞），低于自回歸模型（3.37%（通遼）、4.77%（寶雞））和本文模型（3.82%（通遼）、2.24%（寶雞）），這與該模型以“歷史數(shù)據(jù)擬合最好”為目標(biāo)訓(xùn)練GM(1,1)模型（其中，寶雞：模型階數(shù)為1，為0.022，為4.258；通遼：模型階數(shù)為1，為-0.023，為27.634）有關(guān)，但會造成模型的過擬合，而本文模型在“歷史數(shù)據(jù)擬合最好”這一目標(biāo)的基礎(chǔ)上，增加了“階數(shù)最大（或最小）”目標(biāo)函數(shù)，防止模型出現(xiàn)過擬合，這也是本文模型（其中，寶雞：模型階數(shù)為0.006，為0.046，為-0.010；通遼：模型階數(shù)為0.976，為0.055，為-27.185）關(guān)于非測試集的學(xué)習(xí)誤差大于傳統(tǒng)GM(1,1)模型的原因，但正是因為本文模型沒有對歷史數(shù)據(jù)過度學(xué)習(xí)，減少了對歷史數(shù)據(jù)中噪聲的學(xué)習(xí)，具有較好的預(yù)測效果。

本文模型采用實數(shù)階替代整數(shù)階改進(jìn)傳統(tǒng)灰色模型以正整數(shù)作為階數(shù)的做法，能夠有效提高模型精度[39]，同時本文模型采用反向累加的方法，加大了對新數(shù)據(jù)的利用，使模型能夠充分利用新信息，有效處理新舊信息不一致的問題。增加“階數(shù)最大（或最小）”這一目標(biāo)函數(shù)，能夠防止模型過擬合，增強模型泛化能力，這些也是本模型對測試集預(yù)測誤差小于GM(1,1)模型預(yù)測誤差的原因。

由于農(nóng)業(yè)用水?dāng)?shù)據(jù)具有一定的震蕩性，會對數(shù)據(jù)的自相關(guān)性產(chǎn)生影響，而自回歸模型主要根據(jù)時間序列的前后依存關(guān)系進(jìn)行建模[40]，數(shù)據(jù)的振蕩對模型性能產(chǎn)生影響[41]，因此自回歸模型的預(yù)測效果較差。相對于未對數(shù)據(jù)進(jìn)行轉(zhuǎn)化的自回歸模型，本文增加數(shù)據(jù)轉(zhuǎn)化方法，使得振蕩序列轉(zhuǎn)化為單調(diào)遞減的非負(fù)序列，降低了數(shù)據(jù)的波動性，這也有助于提高本文模型的預(yù)測精度，同時也能擴大模型的適用范圍。

總的來看，本文模型能夠很好地預(yù)測農(nóng)業(yè)用水量，為了進(jìn)一步檢驗?zāi)Ｐ偷男阅埽梦墨I(xiàn)[8]中鄂爾多斯農(nóng)業(yè)用水?dāng)?shù)據(jù)進(jìn)行預(yù)測分析，各模型預(yù)測結(jié)果如表2。

表2 不同模型對鄂爾多斯市農(nóng)業(yè)用水量的預(yù)測結(jié)果

由表2可以看出，除了傳統(tǒng)GM(1,1)模型外(GM(1,1)預(yù)測模型未通過檢測)，各模型的預(yù)測效果都較好，本文模型、自回歸模型和文獻(xiàn)[8]模型的預(yù)測結(jié)果相對誤差分別為1.77%、4.17%和2.87%，其中，本文模型的預(yù)測誤差最小，這說明本文模型對農(nóng)業(yè)用水量的預(yù)測具有一定的適應(yīng)性。

3 結(jié) 論

1）本文建立了改進(jìn)分?jǐn)?shù)階反向累加灰色模型。針對農(nóng)業(yè)用水序列的振蕩性特點和分?jǐn)?shù)階反向累加灰色模型的數(shù)據(jù)要求，提出一種將振蕩序列轉(zhuǎn)化為單調(diào)遞減非負(fù)序列的方法。為了能夠充分利用新數(shù)據(jù)的信息，采用反向累加的方式構(gòu)造模型，并采用分?jǐn)?shù)階“in between”的思想，將階數(shù)擴展到實數(shù)范圍，增強模型的精度。同時，為防止模型過擬合，在傳統(tǒng)目標(biāo)（“歷史數(shù)據(jù)擬合最好”）的基礎(chǔ)上，加入“階數(shù)最大（或最小）”這一目標(biāo)函數(shù)，建立有關(guān)階數(shù)的多目標(biāo)優(yōu)選模型，使用改進(jìn)的NSGA-II對模型進(jìn)行求解，并根據(jù)驗證集擬合的結(jié)果，優(yōu)選出最優(yōu)階數(shù)，結(jié)合分?jǐn)?shù)階反向累加GM(1,1)模型，實現(xiàn)對測試集農(nóng)業(yè)用水量的預(yù)測。

2）為了對模型的性能進(jìn)行對比檢驗，選用內(nèi)蒙古自治區(qū)通遼市和陜西省寶雞市農(nóng)業(yè)用水量為基礎(chǔ)數(shù)據(jù)，將本文模型分別與傳統(tǒng)GM(1,1)模型、自回歸模型、基于小波分析理論組合模型進(jìn)行對比，結(jié)果表明，本文模型對測試集的預(yù)測誤差最小，說明本文模型對于農(nóng)業(yè)用水量預(yù)測具有一定適用性，可為農(nóng)業(yè)用水預(yù)測研究提供支撐。

3）農(nóng)業(yè)用水受氣候條件的影響，而且當(dāng)氣候條件發(fā)生顯著變化時，會對氣候變化前后農(nóng)業(yè)用水?dāng)?shù)據(jù)的一致性造成影響，從而使得在氣候變化前后，歷史數(shù)據(jù)會呈現(xiàn)出不同的模式。模型在訓(xùn)練過程中，如果對氣候變化前的模式過度學(xué)習(xí)，則會對預(yù)測結(jié)果造成一定影響。本文模型訓(xùn)練采用分?jǐn)?shù)階與反向累加的方式，可以給予新數(shù)據(jù)較大的權(quán)重，使得模型學(xué)習(xí)過程中能夠充分利用新信息，加大氣候變化后的模式數(shù)據(jù)學(xué)習(xí)，在一定程度上，考慮不同氣象條件對農(nóng)業(yè)用水的影響。同時，在未來的模型研究中應(yīng)該考慮加入氣候因素，建立更為合理的用水量預(yù)測模型。

區(qū)域農(nóng)業(yè)用水常常被其他行業(yè)用水?dāng)D占，農(nóng)業(yè)用水除了受到自身影響因素的影響外，還受到其他行業(yè)用水情況的影響。因此，農(nóng)業(yè)用水?dāng)?shù)據(jù)的震蕩性也較大。針對這一問題，本文提出一種數(shù)據(jù)轉(zhuǎn)化方法，減少了數(shù)據(jù)的波動性，提高了模型預(yù)測的精度。但是，其他行業(yè)用水與農(nóng)業(yè)用水需求之間存在許多關(guān)聯(lián)，而這些關(guān)聯(lián)具有不確定性，預(yù)測過程較為復(fù)雜，有待于進(jìn)一步深入研究。

[1]王浩，游進(jìn)軍. 水資源合理配置研究歷程與進(jìn)展[J]. 水利學(xué)報，2008，39(10)：1168－1175. Wang Hao, You Jinjun. Advancements and development course of research on water resources deployment[J]. Journal of Hydraulic Engineering, 2008, 39(10): 1168－1175. (in Chinese with English abstract)

[2]王景雷，康紹忠，孫景生，等. 基于貝葉斯最大熵和多源數(shù)據(jù)的作物需水量空間預(yù)測[J]. 農(nóng)業(yè)工程學(xué)報，2017，33(9)：99－106. Wang Jinglei, Kang Shaozhong, Sun Jingsheng, et al. Spatial prediction of crop water requirement based on Bayesian maximum entropy and multi-source data[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2017, 33(9): 99－106. (in Chinese with English abstract)

[3]黃修橋，高峰，王憲杰. 節(jié)水灌溉與21世紀(jì)水資源的持續(xù)利用[J]. 灌溉排水學(xué)報，2001，20(3)：1－5. Huang Xiuqiao, Gao Feng, Wang Xianjie. Water saving irrigation and sustainable utilization of water resources in the 21st century[J]. Journal of Irrigation and Drainage, 2001, 20(3): 1－5. (in Chinese with English abstract)

[4]楊豐順，邵東國，顧文權(quán)，等. 基于Copula函數(shù)的區(qū)域需水量隨機模擬[J]. 農(nóng)業(yè)工程學(xué)報，2012，28(18)：107－112. Yang Fengshun, Shao Dongguo, Gu Wenquan, et al. Stochastic simulation of regional water requirement based on Copula function[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2012, 28(18): 107－112. (in Chinese with English abstract)

[5]張兵，袁壽其，成立，等. 基于L-M優(yōu)化算法的BP神經(jīng)網(wǎng)絡(luò)的作物需水量預(yù)測模型[J]. 農(nóng)業(yè)工程學(xué)報，2004，20(6)：73－76. Zhang Bing, Yuan Shouqi, Cheng Li, et al. Model for predicting crop water requirements by using L-M optimization algorithm BP neural network[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2004, 20(6): 73－76. (in Chinese with English abstract)

[6]萬曉安，李析男，姚軍. 基于經(jīng)濟定額法的農(nóng)業(yè)灌溉需水預(yù)測研究[J]. 人民珠江，2018，39(4)：25－31. Wan Xiaoan, Li Xinan, Yao Jun. Study on the prediction of agricultural irrigation water demand based on economic quota method[J]. Pearl River, 2018, 39(4): 25－31. (in Chinese with English abstract)

[7]常淑玲，尤學(xué)一. 天津市需水量預(yù)測研究[J]. 干旱區(qū)資源與環(huán)境，2008，22(2)：14－19. Chang Shuling, You Xueyi. Prediction of water demand of Tianjin[J]. Journal of Arid Land Resources and Environment, 2008, 22(2): 14－19. (in Chinese with English abstract)

[8]佟長福，史海濱，包小慶，等. 基于小波分析理論組合模型的農(nóng)業(yè)需水量預(yù)測[J]. 農(nóng)業(yè)工程學(xué)報，2011，27(5)：93－98. Tong Changfu, Shi Haibin, Bao Xiaoqing, et al. Application of a combined model based on wavelet analysis for predicting crop water requirement[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2011, 27(5): 93－98. (in Chinese with English abstract)

[9]Wu Hua’an, Zeng Bo, Zhou Meng. Forecasting the water demand in Chongqing, China using a grey prediction model and recommendations for the sustainable development of urban water consumption[J]. International Journal of Environmental Research and Public Health, 2017, 14(11): 1386.

[10]祁洪剛，陳亞寧，李慧敏，等. 基于系統(tǒng)動力學(xué)的新疆焉耆縣水資源需求分析[J]. 第四紀(jì)研究，2010，30(1)：209－215. Qi Honggang, Chen Yaning, Li Huimin, et al. Analysis of water resources based on SD model in yanqi county[J]. Quaternary Sciences, 2010, 30(1): 209－215. (in Chinese with English abstract)

[11]王清印. 預(yù)測與決策的不確定性數(shù)學(xué)模型[M]. 北京：冶金工業(yè)出版社，2000.

[12]劉迪，胡彩虹，吳澤寧. 基于定額定量分析的農(nóng)業(yè)用水需求預(yù)測研究[J]. 灌溉排水學(xué)報，2008，27(6)：88－91. Liu Di, Hu Caihong, Wu Zening. Predicting method for demand of agriculture water based on quantitative analysis[J]. Journal of Irrigation and Drainage, 2008, 27(6): 88－91. (in Chinese with English abstract)

[13]劉磊. 基于遺傳神經(jīng)網(wǎng)絡(luò)的指數(shù)跟蹤優(yōu)化方法[J]. 系統(tǒng)工程理論與實踐，2010，30(1)：22－29. Liu Lei. Index tracking optimization method based on genetic neural network[J]. Systems Engineering-Theory & Practice, 2010, 30(1): 22－29. (in Chinese with English abstract)

[14]Tetko I V, Livingstone D J, Luik A I. Neural network studies. 1. comparison of overfitting and overtraining[J]. Journal of Chemical Information and Modeling, 1995, 35(5): 826－833.

[15]黃雄波，胡永健. 利用自回歸模型的平穩(wěn)時序數(shù)據(jù)快速辨識算法[J]. 計算機應(yīng)用研究，2018，35(9)：2643－2647. Huang Xiongbo, Hu Yongjian. Fast identification algorithm for stationary time series data using autoregressive model[J]. Application Research of Computers, 2018, 35(9): 2643－2647. (in Chinese with English abstract)

[16]黃修橋，康紹忠，王景雷. 灌溉用水需求預(yù)測方法初步研究[J]. 灌溉排水學(xué)報，2004(4)：11－15. Huang Xiuqiao, Kang Shaozhong. Wang Jinglei. A preliminary study on predicting method for the demand of irrigation water resource[J]. Journal of Irrigation and Drainage, 2004(4): 11－15. (in Chinese with English abstract)

[17]鄧聚龍. 灰色預(yù)測模型GM(1, 1)的三種性質(zhì)：灰色預(yù)測控制的優(yōu)化結(jié)構(gòu)與優(yōu)化信息量問題[J]. 華中科技大學(xué)學(xué)報：自然科學(xué)版，1987(5)：1－6. Deng Julong. Properties of grey forecasting models GM(1, 1)[J]. Journal of Huazhong University of Science and Technology: Natural Science Edition, 1987(5): 1－6. (in Chinese with English abstract)

[18]吳利豐，劉思峰，劉健. 灰色GM(1，1)分?jǐn)?shù)階累積模型及其穩(wěn)定性[J]. 控制與決策，2014，29(5)：919－924. Wu Lifeng, Liu Sifeng, Liu Jian. GM(1, 1) model based on fractional order accumulating method and its stability[J]. Control and Decision, 2014, 29(5): 919－924. (in Chinese with English abstract)

[19]劉解放，劉思峰，吳利豐，等. 分?jǐn)?shù)階反向累加離散灰色模型及其應(yīng)用研究[J]. 系統(tǒng)工程與電子技術(shù)，2016，38(3)：719－724. Liu Jiefang, Liu Sifeng, Wu Lifeng, et al. Fractional order reverse accumulative discrete grey model and its application[J]. Systems Engineering and Electronics, 2016, 38(3): 719－724. (in Chinese with English abstract)

[20]吳利豐，付斌. 分?jǐn)?shù)階反向累加GM(1，1)模型及其性質(zhì)[J]. 統(tǒng)計與決策，2017(18)：33－36. Wu Lifeng, Fu Bin. GM (1, 1) model with fractional order opposite-direction accumulated generation and its properties[J]. Control and Decision, 2017(18): 33－36. (in Chinese with English abstract)

[21]練鄭偉，黨耀國，王正新. 反向累加生成的特性及GOM(1, 1)模型的優(yōu)化[J]. 系統(tǒng)工程理論與實踐，2013，33(9)：2306－2312. Lian Zhengwei, Dang Yaoguo, Wang Zhengxin. Properties of accumulated generating operation in opposite-direction and optimization of GOM(1,1) model[J]. Systems Engineering-Theory & Practice, 2013, 33(9): 2306－2312. (in Chinese with English abstract)

[22]錢吳永，黨耀國. 基于振蕩序列的GM(1，1)模型[J]. 系統(tǒng)工程理論與實踐，2009，29(3)：149－154. Qian Wuyong, Dang Yaoguo. GM(1, 1) model based on oscillation sequences[J]. Systems Engineering-Theory & Practice, 2009, 29(3): 149－154. (in Chinese with English abstract)

[23]崔立志. 灰色預(yù)測技術(shù)及其應(yīng)用研究[D]. 南京：南京航空航天大學(xué)，2010. Cui Lizhi. Grey Forecast Technology and Its Application Research[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2010. (in Chinese with English abstract)

[24]曹菲. 隨機振蕩序列的灰色預(yù)測模型及其在氣象系統(tǒng)中的應(yīng)用[D].西安：西安建筑科技大學(xué)，2015. Cao Fei. Grey Forecasting Model of Stochastic Oscillation Sequence and Its Application in Weather System[D]. Xi’an: Xi’an University of Architecture and Technology, 2015. (in Chinese with English abstract)

[25]劉解放，劉思峰，吳利豐，等. 分?jǐn)?shù)階反向累加NHGM(1, 1, k)模型及其應(yīng)用研究[J]. 系統(tǒng)工程理論與實踐，2016，36(4)：1033－1041. Liu Jiefang, Liu Sifeng, Wu Lifeng, et al. Research on fractional order reverse accumulative NHGM(1, 1, k) model and its application[J]. Systems Engineering-Theory & Practice, 2016, 36(4): 1033－1041. (in Chinese with English abstract)

[26]曾亮. 分?jǐn)?shù)階反向累加非等間距GM(1，1)模型及應(yīng)用[J]. 應(yīng)用數(shù)學(xué)和力學(xué)，2018，39(7)：841－854. Zeng Liang. Non-equidistant GM(1, 1) models based on fractional-order reverse accumulation and the application[J]. Applied Mathematics and Mechanics, 2018, 39(7): 841－854. (in Chinese with English abstract)

[27]楊保華，趙金帥. 分?jǐn)?shù)階離散灰色GM(1，1)冪模型及其應(yīng)用[J]. 控制與決策，2015，30(7)：1264－1268. Yang Baohua, Zhao Jinshuai. Fractional order discrete grey GM(1, 1) power model and its application[J]. Control and Decision, 2015, 30(7): 1264－1268. (in Chinese with English abstract)

[28]鄧聚龍. 灰色系統(tǒng)理論教程[M]. 武漢：華中理工大學(xué)出版社，1990.

[29]阿努赫. 水資源短缺條件下現(xiàn)代農(nóng)業(yè)發(fā)展的必由之路：以通遼市、赤峰市為例[J]. 北方經(jīng)濟，2012(15)：45－46. A Nuhe. Only way to develop modern agriculture under the condition of water resources shortage: taking tongliao city and chifeng city as examples[J]. Northern Economy, 2012(15): 45－46. (in Chinese with English abstract)

[30]魏紅俠. 寶雞市農(nóng)業(yè)用水現(xiàn)狀及節(jié)水灌溉措施[J]. 節(jié)水灌溉，2013(8)：73－74. Wei Hongxia. Current situation of agricultural water use in baoji city and water saving irrigation measures[J]. Water Saving Irrigation, 2013(8): 73－74. (in Chinese with English abstract)

[31]Yang L, Kang H S, Zhou Y C, et al. Intelligent discrimination of failure modes in thermal barrier coatings: wavelet transform and neural network analysis of acoustic emission signals[J]. Experimental Mechanics, 2015, 55(2): 321－330.

[32]陳萬成，戴浩然，金映含. 基于數(shù)據(jù)挖掘方法的HEDONIC房屋價格評估模型：以美國城市西雅圖為例[J]. 數(shù)據(jù)分析與知識發(fā)現(xiàn)，2019，3(5)：19－26. Chen Wancheng, Dai Haoran, Jin Yinghan. Appraising home prices with hedonic model: case study of seattle, U.S.[J]. Data Analysis and Knowledge Discovery, 2019, 3(5): 19－26. (in Chinese with English abstract)

[33]于露，金龍哲，王夢飛，等. 基于深度學(xué)習(xí)的人體低氧狀態(tài)識別[J]. 工程科學(xué)學(xué)報，2019，41(6)：817－823. Yu Lu, Jin Longzhe, Wang Mengfei, et al. Recognition of human hypoxic state based on deep learning[J]. Chinese Journal of Engineering, 2019, 41(6): 817－823. (in Chinese with English abstract)

[34]王正新，黨耀國，裴玲玲. 基于GM(1，1)冪模型的振蕩序列建模方法[J]. 系統(tǒng)工程與電子技術(shù)，2011，33(11)：2440－2444. Wang Zhengxin, Dang Yaoguo, Fei Lingling. Modeling approach for oscillatory sequences based on GM (1, 1) power model[J]. Systems Engineering and Electronics, 2011, 33(11): 2440－2444. (in Chinese with English abstract)

[35]王正新. 基于傅立葉級數(shù)的小樣本振蕩序列灰色預(yù)測方法[J]. 控制與決策，2014，29(2)：270－274. Wang Zhengxin. Grey forecasting method for small sample oscillating sequences based on Fourier series[J]. Control and Decision, 2014, 29(2): 270－274. (in Chinese with English abstract)

[36]方睿，朱碧穎，粟藩臣. 基于模擬退火思想的遺傳算法參數(shù)選擇[J]. 計算機應(yīng)用，2014，34(S1)：114－116，126. Fang Rui, Zhu Biying, Su Fanchen. Genetic algorithm parameter tuning based on simulated annealing[J]. Journal of Computer Applications, 2014, 34(S1): 114－116,126. (in Chinese with English abstract)

[37]Jacquez J A．Design of experiments[J]. Journal of the Franklin Institute, 1998, 335(2): 259－279．

[38]劉思峰. 灰色系統(tǒng)理論及其應(yīng)用. [M]. 第5版，北京：科學(xué)出版社，2010.

[39]Wu Lifeng, Liu Sifeng, Yao Ligen, et al. Grey system model with the fractional order accumulation[J]. Communications in Nonlinear Science and Numerical Simulation, 2013, 18(7)：1775－1785.

[40]湯成友，官學(xué)文，張世明. 現(xiàn)代中長期水文預(yù)報方法及其應(yīng)用[M]. 北京：中國水利水電出版社，2008.

[41]牛軍宜，馮平. 基于Markov狀態(tài)切換的水質(zhì)時序自回歸預(yù)測模型[J]. 吉林大學(xué)學(xué)報：地球科學(xué)版，2010，40(3)：657－664. Niu Junyi, Feng Ping. Water quality time series prediction based on markov switching autoregression model[J]. Journal of Jilin University：Earth Science Edition, 2010, 40(3): 657－664. (in Chinese with English abstract)

Prediction of agricultural water consumption based on fractional grey model

Li Jun1, Song Songbai1※, Guo Tianli1, Wang Xiaojun2,3

(1.,,712100,; 2.,,210029,; 3.,210029,)

Due to the shortage of water resources, serious water pollution, improper use of water and the occupation of agricultural water rights by other industries, China's agriculture will face the risk of water shortage in the future. Due to the amount of water resources in North China is relatively small compared with that in South China, coupled with extensive operating methods and the low level of agricultural irrigation technology, water resources are wasted seriously, the problem of agricultural water shortage in North China is more serious. Optimal allocation of water resources is one of the main measures to alleviate the shortage of agricultural water resources, and is an important means to achieve sustainable use of water resources. Accurate prediction of regional agricultural water consumption is the key to optimal allocation of water resources. Grey model is a method to study “poor information”, “small sample” and uncertainty problems, which is widely used in economics, finance and other fields. The amount of historical data of annual agricultural water consumption is not enough, which is affected by many factors, and has concussion. Therefore, it is suitable to use grey model to predict agricultural water consumption. The oscillation characteristics of agricultural water consumption data series have a certain impact on the prediction accuracy of the model. To resolve these problems, an improved fractional grey prediction model is proposed in this paper. Based on the monotonically decreasing non-negative series which transformed from the oscillation series of the agricultural water consumption, a multi-objective optimization model was constructed according to the two objective functions of “maximum (or minimum) order” and “the best fit of historical data”, which was solved by the improved non-dominated sorting genetic algorithm II (NSGA-II) method. Agricultural water consumption in the test set for the research areas of Tongliao city (42°15′N-45°59′N, 119°14′E-123°43′E), Ordos city (37°35′24″N-40°51′40″N, 106°42′40″E-111°27′20″E) of Inner Mongolia autonomous region and Baoji city(33°35′N-35°06′N,106°18′E-108°03′E) of Shaanxi province was predicted by the grey model (GM(1,1)) model of fractional order reverse accumulation, the order of which was optimized according to the results of the test set fitting. The average error of the prediction was 2.23%,1.77% and 0.31%, respectively. In order to test the performance of the model, the model proposed in this paper was compared with the traditional GM (1,1) model, traditional autoregressive model and the combined model based on the wavelet analysis theory respectively. Among them, the average prediction error of GM(1,1) model for the Tongliao and Baoji city is 5.55% and 1.28%, but the detection is failed for the Ordos city. The average prediction error of autoregressive model for the three research areas is 3.34%, 4.17% and 6.49%. The average prediction error of agricultural water consumption in Ordos City of Inner Mongolia Autonomous Region based on the combination model of wavelet analysis theory is 2.87%. The results show that compared with GM(1,1) model, the prediction effect of the model in this paper is better, which depends on the objective function of “the best fitting of historical data” and the objective function of “the largest (or the smallest) order” to reduce the learning degree of the model for noise, because the model in this paper transforms the oscillating data and reduces the uncertainty of the data, so compared with the autoregressive model without data processing, the model in this paper is less affected by data volatility. In this paper, the idea of fractional order “in between” is used to improve the traditional gray model with positive integer as order, which can effectively improve the accuracy of the model. At the same time, the method of reverse accumulation is used to increase the use of new data. On the whole, for the prediction of agricultural water consumption in all research areas, the model in this paper has the minimum error, strong generalization ability and certain practicability, which can provide a basis for the prediction of regional agricultural water consumption and the allocation of agricultural water resources in northern China.

agriculture; water; models; fractional order; grey prediction; oscillation sequence; overfitting; multi-objective optimization

李 俊，宋松柏，郭田麗，王小軍. 基于分?jǐn)?shù)階灰色模型的農(nóng)業(yè)用水量預(yù)測[J]. 農(nóng)業(yè)工程學(xué)報，2020，36(4)：82－89. doi：10.11975/j.issn.1002-6819.2020.04.010 http://www.tcsae.org

Li Jun, Song Songbai, Guo Tianli, Wang Xiaojun. Prediction of agricultural water consumption based on fractional grey model[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2020, 36(4): 82－89. (in Chinese with English abstract) doi：10.11975/j.issn.1002-6819.2020.04.010 http://www.tcsae.org

2019-05-06

2020-01-02

中央財政水資源節(jié)約、管理與保護(hù)項目（126302001000150005）；國家自然科學(xué)基金項目（51479171、51179160、50879070）

李 俊，博士生，主要從事水資源優(yōu)化配置研究。Email：13707513643@163.com

宋松柏，教授，博士，主要從事水文水資源研究。Email：ssb6533@nwsuaf.edu.cn

10.11975/j.issn.1002-6819.2020.04.010

TV213.4

A

1002-6819(2020)-04-0082-08