基于非序貫蒙特卡洛的電網調度風險評估*

羅 慶，謝曉帆

(國網江西省電力公司 贛州供電公司，江西 贛州 341000)

我國輸配電網絡規模日益擴大，逐漸朝著超高壓和遠距離方向發展[1]，同時，電力系統的結構、運行方式以及電網中的不確定因素也變得日趨復雜，這對電網的影響日益明顯，并造成了巨大的經濟損失.因此，評估電網調度的風險可以有效減少電力系統的故障概率，從而降低損失[2].

要保證電網運行風險評估的有效性和精確性，需要根據電力系統的發電站、變電站、輸電子系統和配電子系統等各功能部分的特點使用不同的評估方法，以實現最優的評估效果[3].目前，常用的電網調度風險評估方法主要分為模擬法和解析法兩類，其中，解析法通過建立嚴格、精確的數學模型來求取各種風險指標；而模擬法利用計算機和隨機數的產生原理，采用重復模擬一個過程的實現、隨機抽樣和統計的方法來計算調度系統風險指標的近似值[4].模擬法使用隨機數來模擬物理和數學問題，以解決確定性問題與帶有隨機性的問題，包括非序貫模式和序貫模式兩種[5-6].其中，非序貫蒙特卡洛模擬不需要考慮系統的實際運行順序，只通過抽取大量的樣本數據即可評估系統運行風險指標；而序貫模式則需要按照系統運行的時間順序和運行歷史來計算風險指標.解析法則需要根據系統設計和元件的故障數據來推導系統的風險指標，主要包括狀態空間法、網絡分析法、狀態枚舉法和故障樹分析法[7-8].

模擬法與解析法均包括狀態選擇、狀態估計和指標計算三個步驟.其中，解析法使用枚舉的方法進行狀態選擇，并計算風險指標的解析解[9]；而模擬法使用抽樣的方法進行狀態選擇，用統計法計算風險指標[10].解析法通常具有清晰的物理模型和概念，并能獲得較高的評估精度，但其需要處理復雜的關聯事件，且在模擬實際控制策略時會遇到較大困難；而模擬法的采樣次數與系統的規模無關，易于處理各種實際運行策略，但需要進行多次模擬來獲取較高的評估精度，且當系統參數變化時需要重新模擬[11].

針對上述問題，本文結合解析法和模擬法的特點提出了一種基于非序貫蒙特卡洛的電網調度風險評估方法.首先在非序貫蒙特卡洛模擬的基礎上結合解析法來提高計算效率，然后提出了一種等分散抽樣法來減小采樣方差，從而提高收斂效率，最后，在IEEE RTS系統上進行仿真測試來驗證所提出方法的有效性.

1 解析法與非序貫蒙特卡洛模擬

本文通過在模擬過程中結合解析法和蒙特卡洛模擬來解析判斷采樣狀態，從而減少系統評估所需的時間，充分發揮解析法計算精度高和蒙特卡洛模擬法計算量小的優勢，在蒙特卡洛模擬過程中使用解析法來減少采樣次數.

假設電網調度系統只考慮供電線路和發電機的故障，則可將隨機采樣后的系統狀態劃分為如圖1所示的4個區域.

圖1中GF和GN分別表示發電機處于故障狀態和正常運行狀態，TF和TN分別表示輸電線路處于故障狀態與正常運行狀態.圖1中Ⅰ區為正常運行狀態，其他區域為故障狀態，其中，Ⅳ區表示同時出現發電機和線路故障.由于配電系統在不同故障狀態出現系統切負荷的概率不同，故本文將Ⅱ、Ⅲ和Ⅳ區劃分為不引起系統切負荷的狀態集合和可能引起系統切負荷的狀態集合.本文首先計算判斷采樣狀態是否屬于不引起系統切負荷的狀態，若屬于則不會影響配電系統的風險指標，立即轉入下次采樣；否則會影響系統的風險指標，需應用削減負荷.

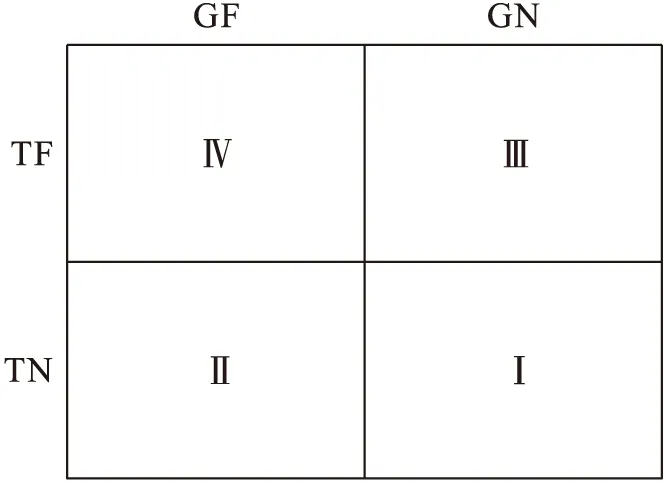
圖1 系統狀態劃分圖Fig.1 Partition diagram of system states

解析法判斷流程如圖2所示.其中，GF=1和GN=1分別表示發電機與輸電線路故障；GF=0和GN=0分別表示發電機和輸電線路正常工作.

當出現發電機故障時，該發電機節點備用容量能夠彌補故障，導致有功出力損失時需重置GF=0，即

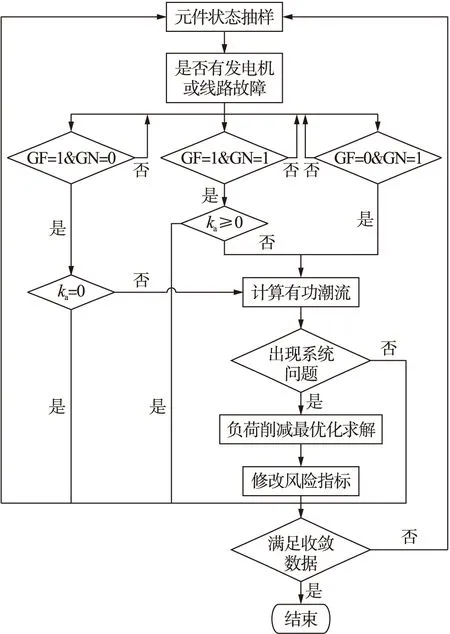
圖2 解析法判斷流程Fig.2 Flow chart of judgment with analytic method

(1)

式中：P′c和Pc分別為發電機的有功功率上限和實際有功功率；P′gc和Pgc分別為發生故障前后的有功功率；ka≥0表示該節點的有功注入功率不變.本文通過在發電機或線路故障時計算各線路的有功潮流來判斷線路是否過負荷，從而判定是否需要削減負荷.

2 抽樣方差減小技術

在進行電網調度風險評估時，為了獲得更高的風險指標，通常需要對數目龐大的系統隨機狀態進行評估，需要花費較長的計算時間.本文提出了一種等分散抽樣方法，通過降低抽樣方差在保證計算精度的前提下，顯著減少采樣次數來提升計算速度.

等分散抽樣法將采樣區間[0，1]等分成k個不同長度的子區間，其中k滿足max(f1，f2，…，fm)≤k<1，f1，f2，…，fm為m個系統元件的強迫失效概率.

對于某一元件i的狀態值xi，可按照式(2)在k個子區間中采樣k個狀態變量xi1，xi2，…，xij，…，xik，即

(2)

由式(2)可知，每隨機抽樣一次可以根據抽樣結果得到k個狀態，從而有效提高了采樣效率.本文將k個狀態的風險指標值F(x1)，F(x1)，…，F(xi)，…，F(xk)的平均值作為隨機變量xi的風險指標值.

本文采用系統停電功率期望EP和停電概率TP作為風險指標，其定義分別為

(3)

(4)

式中：PLi為負荷總量；PGi為發電出力總量.可以得到本文的風險指標為

(5)

其期望值為

(6)

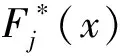
(7)

3 電網調度風險評估流程

本文將解析法和方差減小技術加入到傳統的非序貫蒙特卡洛模擬法中，以實現更高的評估效率.其中，通過引入解析法來減少單次抽樣模擬所需的時間，并采用等分抽樣法在保證計算精度的同時減少抽樣次數.所提出改進方法的計算流程如圖3所示.

圖3 改進的非序貫蒙特卡洛模擬法計算流程Fig.3 Calculation flow chart of improved non-sequentialMonte Carlo simulation method

改進的非序貫蒙特卡洛模擬法采用等分散抽樣的方法隨機抽取系統的狀態.假設該調度控制系統包含N個元件，當進行均勻抽樣時每次抽取只能得到一個系統狀態；而采用等分散抽樣后，每次抽樣可以生成元件的k個狀態，并得到k個系統狀態，從而大幅提高抽樣效率.該方法在系統狀態抽樣結束后，先進行解析判斷再評估系統狀態與計算風險指標，由此便能減少單次抽樣模擬所需的時間，從而提高效率.

4 算例分析

本文使用如圖4所示的IEEE RTS系統進行仿真測試，來驗證所提出方法的有效性.該系統包含32臺發電機、33條輸電線路和24條母線，以及17個裝機總容量為3 410 MW，平均負荷率為62.44%的電源.

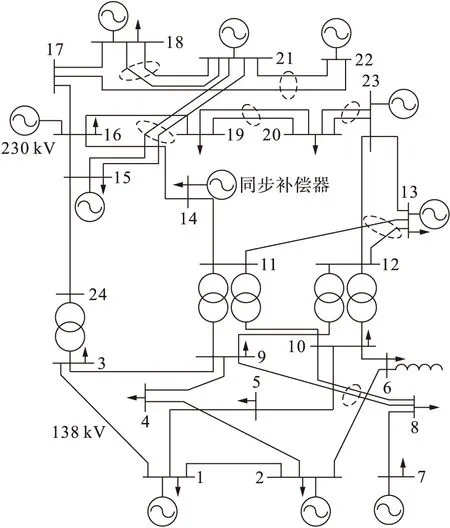
圖4 IEEE RTS系統網絡圖Fig.4 Diagram of IEEE RTS system network

將所提出的方法(方法Ⅲ)與傳統采用分散抽樣的非序貫蒙特卡洛模擬法(方法Ⅰ)和采用均勻抽樣的非序貫蒙特卡洛模擬法(方法Ⅱ)進行比較，以驗證所提出的方法具有更高的計算效率.使用系統停電功率期望EP和停電概率TP作為該系統的風險指標.

表1為3種方法的風險評估結果，其中，VEP和VTP分別為系統停電功率期望EP與停電概率TP的方差；ηEP和ηTP分別為其對應的方差系數.本文分別比較了抽樣次數為5 000、10 000、15 000、20 000、25 000、30 000、35 000、40 000、45 000和50 000時，各方法的風險指標值.從表1中可以看出，在相同的抽樣次數下，本文方法能明顯降低抽樣方差，并能提高收斂速度.在采樣次數為50 000時，本文方法所獲得的ηEP和ηTP分別為方法Ⅰ的20.06%和21.18%，方法Ⅱ的21.05%和21.08%，表明本文方法的收斂性能更優.

表1 各方法風險評估結果Tab.1 Risk assessment results of various methods

圖5、6分別為各種方法的停電功率期望EP和停電概率TP的方差系數變化曲線.從圖5、6中可以看出，隨著抽樣次數的增加，各方法的方差系數均在減小，且相比于采用分散抽樣的非序貫蒙特卡洛模擬法和采用均勻抽樣的非序貫蒙特卡洛模擬法，本文方法具有更小的方差系數.

圖5 停電功率期望方差系數變化曲線Fig.5 Expected variance coefficient change of power outage

圖6 停電概率方差系數變化曲線Fig.6 Variance coefficient change of power outage probability

采用分散抽樣的非序貫蒙特卡洛模擬法和采用均勻抽樣的非序貫蒙特卡洛模擬法進行風險評估時，在不同的抽樣次數下所耗費的時長占比均為100%.而本文進行5 000～50 000次采樣時，所耗費的時長占比分別為29.39%、32.12%、31.76%、32.4%、31.78%、32.7%、32.47%、32.21%、31.41%和32.3%，由此表明，本文所提出的方法可以節省70%以上的計算時間.

5 結 論

本文結合解析法和模擬法的特點，提出了一種基于非序貫蒙特卡洛的電網調度風險評估方法.該方法在非序貫蒙特卡洛模擬的基礎上結合解析法來提高計算效率，同時使用方差減小技術來提高收斂效率.基于IEEE RTS系統的仿真測試與實驗結果表明，所提出的方法能節省70%以上的計算時間，且具有更高的計算效率.