密鑰共享下跨用戶密文數據去重挖掘方法*

高永強

(呂梁學院 計算機科學與技術系，山西 離石 033000)

大數據信息處理過程中，數據通過密文的形式存儲在云空間中，因此，需要對密鑰共享下跨用戶密文數據進行優化挖掘，相關密鑰共享下跨用戶密文數據去重挖掘方法研究受到學者的主要關注[1].對密鑰共享下跨用戶密文數據的去重挖掘處理是建立在對數據的特征提取和分類識別基礎上的，傳統方法中，對密鑰共享下跨用戶密文數據去重挖掘分析方法主要有模糊C均值去重挖掘方法、K均值去重挖掘方法、網格去重挖掘方法等[2-3].采用模糊C均值聚類識別方法提取密鑰共享下跨用戶密文數據的特征量，根據特征提取結果進行數據的去重挖掘，采用主成分分析法進行特征提取，但該方法在處理密鑰共享下跨用戶密文數據時模糊度較大，自適應性能不好.本文提出了基于關聯信息特征提取的密鑰共享下跨用戶密文數據去重挖掘方法，結合非線性統計序列分析方法進行密鑰共享下跨用戶密文數據的統計特征采樣，分析跨用戶密文數據的隨機編碼特征分布結構；采用空間欠采樣方法進行密鑰共享下跨用戶密文數據的關聯特征檢測，結合深度學習方法進行密鑰共享下跨用戶密文數據挖掘過程中的自適應尋優和數據挖掘優化，展示了本文方法在提高密鑰共享下跨用戶密文數據去重挖掘能力方面的優越性能.

1 數據的存儲配置結構和特征分析

1.1 密文數據分布式存儲結構模型

為了實現對密鑰共享下跨用戶密文數據去重挖掘算法的優化設計，對密鑰共享下跨用戶密文數據存儲結構模型進行特征重組[4]，建立密鑰共享下跨用戶密文數據體系結構模型，假設Φ(z)=(h(z)，h(φ1(z))，…，h(φ2d(z)))T表示一個采樣節點分布集，則密鑰共享下跨用戶密文數據采集的標簽分布集為

(1)

式中：ω為標簽分布權重；yi為跨用戶密文數據i的自相關函數集合；a為跨用戶密文數據標簽相關性參數；bi為密文數據尺度系數；γij為密文數據.

結合向量量化分析方法，構建密鑰共享下跨用戶密文數據存儲節點最優分布模型，用一個二元有向圖G=(V，E)表示密鑰共享下跨用戶密文數據的圖模型結構，其中，V為部署存儲鏈路中的頂點集；E為密鑰共享下跨用戶密文數據在有限域分布區域G中所有邊的集合.假設M1，M2，…，MN為密鑰共享下跨用戶密文數據的Sink節點，采用歐式距離表示密鑰共享下跨用戶密文數據傳輸節點的模糊關聯集，采用分塊區域融合方法進行數據的量化配置和線性加密[5]，自適應加權系數為W={w1，w2，…，wk}.在密鑰共享下跨用戶密文數據的信息覆蓋區域，假設M個節點的加密關聯配對集為x(k-1)，x(k-2)，…，x(k-M)，特征篩選的空間分布權系數為xs=[x1(η1)，x2(η2)，…，x(ηN)]T，則相似度特征值估計式為

(2)

式中：Yi為特征向量矩陣；|M|為節點間歐式距離.

根據源域和目標域的關聯規則屬性，得到密鑰共享下跨用戶密文數據的統計特征集為

(3)

式中：A′為跨用戶密文數據的模糊項；r為關聯規則.

利用含有樞紐特征的樣本進行存儲結構的分布式設計[6]，得到分布式存儲結構模型為

(4)

式中：e為數據預測特征；α為密文數據的置信度；p為密鑰共享下跨用戶密文數據Source與Sink節點之間的負載；ε(t)為概率t分布值；K為密鑰共享下跨用戶密文數據在分布式存儲結構模型中的嵌入維數；τ為密鑰共享下跨用戶密文數據在高維相空間中的嵌入延遲.

根據上述分析構建密鑰共享下跨用戶密文數據存儲結構模型，根據數據存儲的節點分布屬性進行去重挖掘[7].

1.2 跨用戶密文數據的隨機編碼特征分布

結合非線性統計序列分析方法進行密鑰共享下跨用戶密文數據的統計特征采樣，分析跨用戶密文數據的隨機編碼特征分布結構，在密鑰共享跨用戶密文數據的關聯調度集中[8]，模糊調度點集滿足D∈Rm×M，得到數據的類標信息和詞性分布關系為

(5)

根據目標域的文本進行特征變換，密鑰共享下跨用戶密文數據最優去重挖掘特征分量為

(6)

式中，dk為目標域的數據點與第k個聚類中心間的距離.

采用特征集成及樣本選擇算法，得到隨機編碼特征值為

f=R{[i，C][j，C]}

(7)

式中，C=[c1，c2，…，cg]為密鑰共享下跨用戶密文數據的分塊匹配集，采用向量量化編碼方法進行數據的密鑰構造[9]，得到密鑰構造協議表達式為

(8)

式中：?為分塊匹配系數；β為映射系數.計算非樞紐映射特征，根據密鑰構造協議進行聯合關聯挖掘，得到互信息量為

(9)

式中：B為密鑰共享下跨用戶密文數據的檢測幅值；ρ為信源域與目標域的遷移調節參數，根據隨機編碼特征檢測結果進行密文數據的去重挖掘設計[10]；θ為時間.

2 數據去重挖掘優化

2.1 密文數據的關聯特征檢測

在結合非線性統計序列分析方法進行用戶密文數據統計特征分析的基礎上，本文進行了密文數據的去重挖掘設計，提出了基于關聯信息特征提取的密鑰共享下跨用戶密文數據去重挖掘方法.通過識別不同領域的主題特征量進行密文數據的線性編碼設計[11]，抽取密鑰共享下跨用戶密文數據的平均互信息特征量，輸出密鑰共享下跨用戶密文數據的屬性分布互信息.采用標簽識別技術進行數據編碼的融合處理[12]，得到密鑰共享下跨用戶密文數據的模糊C均值聚類分布集為

(10)

式中，q為融合特征.使用源域的領域特有特征進行密鑰共享下跨用戶密文數據融合[13]，需要同時滿足

(11)

式中，E為收斂性判斷閾值.

對密鑰共享下跨用戶密文數據模糊信息進行主成分分析，根據多種詞匯語義關系進行線性映射，設{u1，u2，…，uN}表示包含元素節點集合的密鑰共享下跨用戶密文數據的空間分布集合，{v1，v2，…，vM}表示源域的領域特征分布集合，O=[Ou，v]N×M表示密鑰共享下跨用戶密文數據的用戶行為集，對挖掘的數據進行特征篩選和屬性聚類[14]，實現數據去重挖掘中心的自適應尋優，采用深度學習算法得到尋優迭代式為

(12)

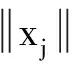
2.2 數據去重挖掘輸出

假設待挖掘的密鑰共享下跨用戶密文數據信息流的統計分布序列為{z1，z2，…，zN}，令z(n)為一組回歸分析特征量，在重構相空間中進行密鑰共享下跨用戶密文數據的稀疏散亂點映射，得到密鑰共享下跨用戶密文數據的分布式重組結構式，并將領域共有詞作為樞紐特征，得到密鑰共享下跨用戶密文數據的概念集表達式，最后根據樞紐特征最相似性，得到第i個密鑰共享下跨用戶密文數據的稀疏散亂點集Pi.根據領域共有詞的特征分布集進行密鑰共享下跨用戶密文數據的回歸分析和重構，在同一近義詞簇中得到密鑰共享下跨用戶密文數據的加密密鑰關系為A→B，B→C，結合深度學習方法進行密鑰共享下跨用戶密文數據挖掘過程中的自適應尋優，采用匹配濾波方法實現密文數據的去重處理，得到去重挖掘輸出為

(13)

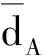
3 仿真實驗與結果分析

為了驗證本文方法在實現密鑰共享下跨用戶密文數據去重挖掘中的應用性能，結合Matlab和C++編程軟件進行仿真實驗分析，密鑰共享下跨用戶密文數據的采樣樣本數據庫來自于云組合數據庫PearsonDatabase.跨用戶密文數據集為800個，從中隨機選取訓練數據集，訓練數據集規模為100×100，向量維度為3，設定跨用戶密文數據采樣的時間為5s，迭代次數為500次，密文數據的采樣時間延遲為0.18s，信源域與目標域的遷移調節參數為255，收斂性判斷閾值為60.根據上述仿真環境和參數設定對密鑰共享下跨用戶密文數據進行去重挖掘處理，得到數據分布的時域波形如圖1所示.

從圖1中可以看出密文數據分布的時域波形變化較為劇烈，波形邊緣出現大量離散點.以圖1數據為研究對象，抽取密鑰共享下跨用戶密文數據的平均互信息特征量，結合深度學習方法進行密鑰共享下跨用戶密文數據挖掘過程中的自適應尋優，在尺度系數為0.2和0.4情況下對密文數據進行特征重構，得到數據挖掘的特征重構輸出如圖2所示.

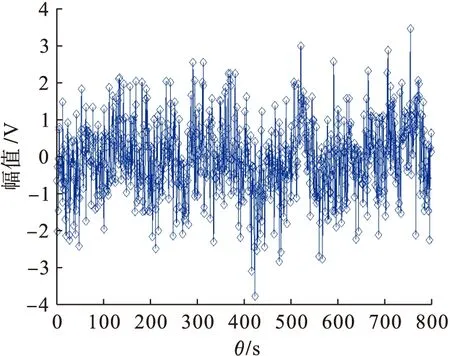
圖1 密文數據分布時域波形Fig.1 Time domain waveform of ciphertext data distribution

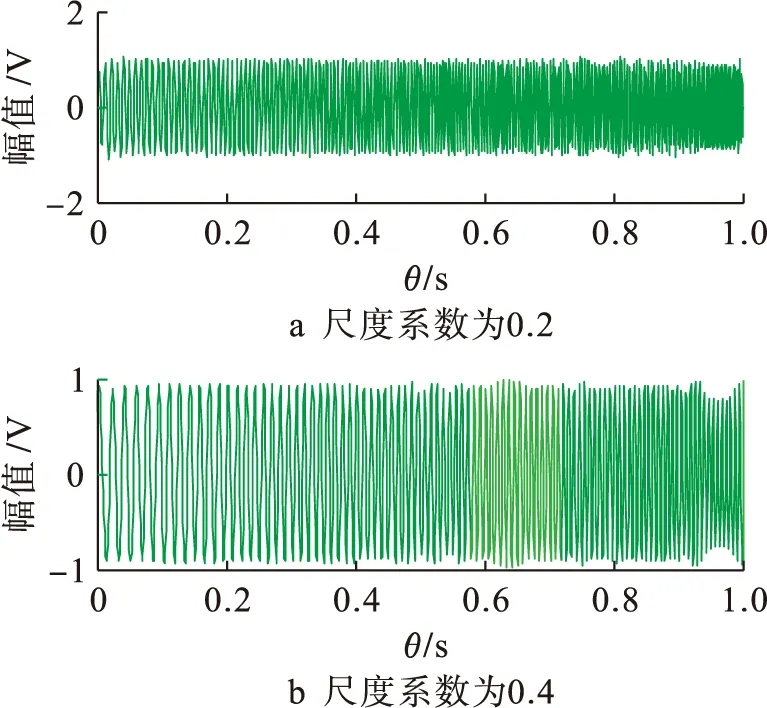
圖2 密文數據的特征重構Fig.2 Feature reconstruction of ciphertext data

由圖2可以看出，特征重構后的密文數據波形幅度較為一致，邊緣離散數據與圖1相比改善效果明顯.尺度系數為0.2時，密文數據特征重構的效果更好，但從波形范圍來說，仍具有多樣特征重合的特性，數據去重不夠準確，因此選用尺度系數為0.4的密文數據特征重構結果與粒子群去重挖掘方法及K均值去重挖掘方法進行對比分析，得到的輸出結果如圖3所示.

分析圖3可知，所提方法的據挖掘優化輸出幅值波動較小，穩定性較高.在密鑰共享下跨用戶密文數據挖掘的去重性較好，測試挖掘誤差對比結果如表1所示.

分析表1可知，本文方法經過多次迭代，挖掘誤差始終低于K均值去重挖掘方法和粒子群去重挖掘方法，說明本文方法的去重性較好，誤差較低.在單位數據空間下，采用本文方法與其他兩種算法對100個數據集進行聚合能力測試，所得結果如圖4所示.

由圖4可以看出，采用本文方法數據較為聚攏，數據簇沒有出現離散數據點；粒子群去重挖掘方法數據簇出現少量離散點；K均值去重挖掘方法數據簇中出現了大量離散點，由此可以看出所提方法比其他兩種算法的數據聚合能力強.

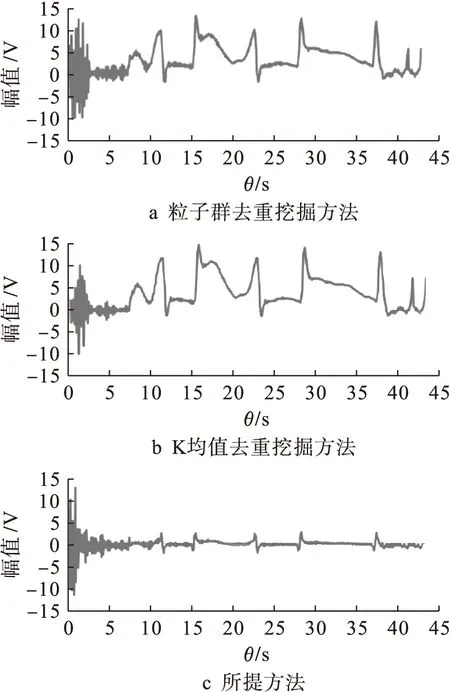
圖3 不同方法的數據挖掘優化輸出Fig.3 Data mining optimization and output of different methods

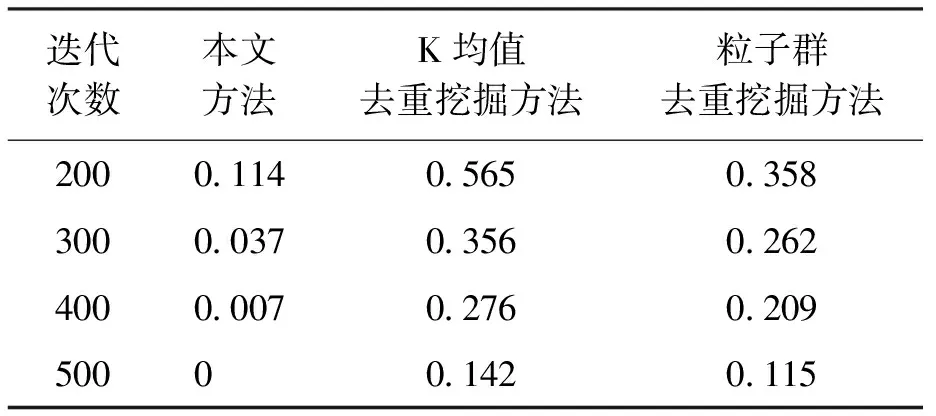
表1 誤差對比Tab.1 Error comparison %

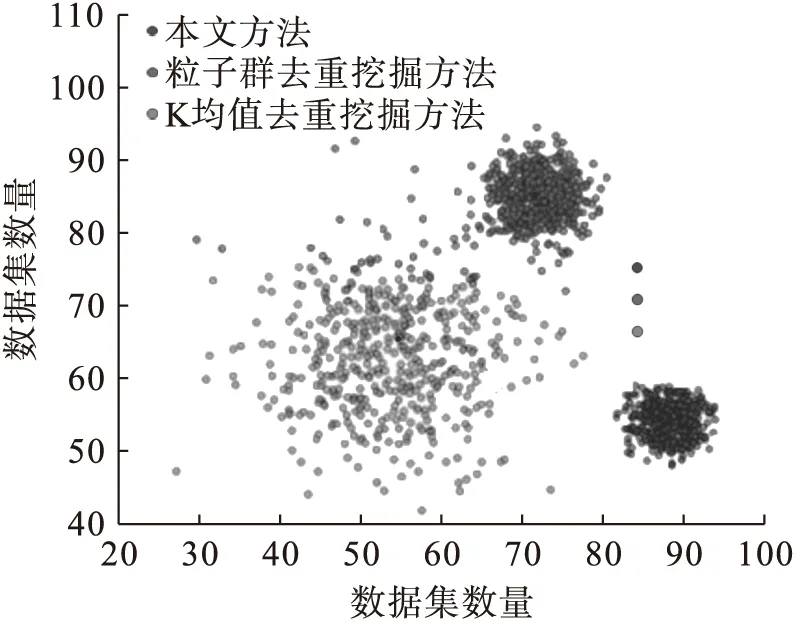
圖4 數據聚合能力對比Fig.4 Comparison of data aggregation capabilities

4 結 論

本文構建了密鑰共享下跨用戶密文數據的并行聚類分析模型，建立了密鑰共享協議，并采用網格分區域調度方法實現密文數據編碼和優化調度.結合非線性統計序列分析方法進行密鑰共享下跨用戶密文數據的統計特征采樣，分析跨用戶密文數據的隨機編碼特征分布結構，結合深度學習方法進行密鑰共享下跨用戶密文數據挖掘過程中的自適應尋優，采用匹配濾波方法實現密鑰共享下跨用戶密文數據的去重處理.通過仿真研究得知，本文方法在進行密文數據挖掘時，去重性較好，誤差較低，且數據聚合能力強.